异地分布式敏捷开发团队协作合作博弈研究

殷茗, 蒋丹, 马静, 邓国林

(1.西北工业大学 软件与微电子学院, 陕西 西安　710072; 2.上海飞机客户服务有限公司, 上海　200241)



异地分布式敏捷开发团队协作合作博弈研究

殷茗1, 蒋丹1, 马静2, 邓国林1

(1.西北工业大学 软件与微电子学院, 陕西 西安710072; 2.上海飞机客户服务有限公司, 上海200241)

摘要：在分布式敏捷开发过程中，为了实现异地合作各方之间的快速响应与反馈，需要解决其敏捷协同协作问题。针对异地分布式敏捷协作开发过程，提出了其适应性团队协作的一种改进框架，该框架运用合作博弈理论，从核心、核仁、夏普利值分别展开。核心确定了异地分布式合作各方为稳定的分配集，核仁的分配结果实现较为困难，重点通过夏普利值分析进行了合作博弈夏普利值的分配，团队协作夏普利值相关数据表明，客户和本地团队对团队协作的边际贡献较大，而异地分布式团队的边际贡献较小。

关键词：异地分布式；敏捷开发；团队协作；博弈

近年来，异地分布式敏捷开发团队越来越多，许多公司纷纷采用了分布式敏捷开发方法。Ansgar等[1]阐明，异地分布式敏捷开发以其轻量级、简单、快速交付商业价值等特征，得到了软件业界的广泛关注。在异地分布式敏捷软件开发过程中，客户、设计人员、开发人员、管理人员之间会产生许多关于协作方面的问题。因此，团队协作不仅是异地敏捷软件开发中应首先解决的问题，而且是异地敏捷项目获得成功的关键。本文根据合作博弈理论，研究分析了异地敏捷团队协作的相关问题。从合作博弈理论的角度，对团队协作模型进行分析，首先分析了团队协作模型中的特征函数及其性质。其次分析了合作博弈问题几种常用的解，并以此验证用于研究的可行性。最后，选用夏普利值对团队协作模型进行分析，给出了一种团队协作的合作博弈夏普利值分配。

1异地分布式敏捷开发团队协作理论框架

Malone[2]最先提出了团队协作理论，他认为当大量参与者聚集在一起追求相同目标时，必须以实际行动把自己组织起来；而当只有一个参与者时并不会这样做。Nguyen-Duc等[3]提出了通过正式及非正式交流，使得本地团队能够清晰了解团队成员的特长，并将任务分配给团队开发成员。在开发过程中，本地团队可以通过非正式交流和使用说明书；但对于异地分布式团队，由于时差、地域、社会文化等问题，使交流、协作、控制过程变得复杂，需要比本地团队更多的开发时间。Wiredu[4]认为异地分布式软件开发过程中的协作问题可能涉及多个维度，主要聚焦于开发者、过程、信息、技术及它们之间的交互，因而提出了一个异地分布式软件开发模型，该研究主要在理论方面提出了异地分布式开发模型，其有效性和可靠性尚待进一步研究和验证。

项目管理者在软件开发人员和其他成员之间充当非常重要的协调角色，包括传递进度控制报告、搜集团队成员所需要的信息等[5]。在不确定条件下，当协作行为得不到保障时，开发人员则倾向于不协作，且软件开发活动是基于人的知识密集型的活动，成本、开发产出、需求的不确定性等都会给开发活动带来挑战[6]。团队协作是由一系列协调机制组成，且每一个协调机制都强调在特定情形下的独立性。在研究协作理论时，重要的任务之一是识别出各个任务之间的依赖关系。根据这些依赖关系，对协作中的任务进行分类[7]。综上所述，异地分布式敏捷开发团队协作研究中，包括了人员的技术和劳动、开发成员之间的关系、团队成员承担开发任务的差异性、项目管理者的作用及协作机制等。这些因素综合影响着团队成员内部协作过程和效果。本文结合异地分布式敏捷开发团队协作的背景，建立了异地分布式敏捷开发团队协作整体模型如图1所示。

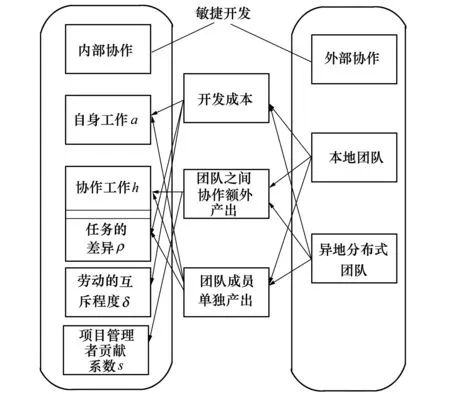
图1　异地分布式敏捷开发团队协作整体框架

图1中，单向箭头指向被影响一方。即团队内部协作受团队成员单独产出、团队成员之间协作额外产出、开发成本的影响，而以上3个因素均受任务的差异ρ、自身工作a、协作工作h、劳动的互斥程度δ、项目管理者贡献系数s的影响；本地团队、异地分布式团队、客户之间相互影响、相互作用及它们之间协作产出的变化情况，是本文研究的核心内容。

2团队协作合作博弈分析与求解

2.1特征函数

通常，合作博弈中的参与者通过制定可信的承诺，来协调相互之间的选择。在异地分布式团队与本地团队进行协调和协作的过程中，以增加各个团队产出及寻求协作稳定为合作博弈目标，在协作过程中，各个团队可不断调整自己的行为，进而改变博弈结果。

定义1给定一个有限的参与人集合N,合作博弈的特征型是有序数对(N, v),其中特征函数v是一个从集合2N={S|S⊆N}到实数集RN的映射,即v:2N→RN,且v(ø)=0。

本文所用到的特征函数定义如下:

v(1) 即如果仅有客户,则该软件开发过程是无意义的,此时,v(1)=0;

v(2),即使本地团队选择协作,若没有客户的协作参与和提供需求,此时仍有v(2)=0;

v(3),同理,仅有异地分布式团队的参与,若没有客户的参与,仍有v(3)=0;

v(1,2),即本地团队选择同客户进行协作开发,协作产出为:

v(1,2)=αE2+αC2+R2-C2+c

v(1,3),即异地分布式团队同客户进行协作开发,协作产出为:

v(1,3)=Da*(βE3+R3)+(βC3-C3)/Da+c

v(2,3),即本地团队同异地分布式团队进行协作,客户参与度不高,与敏捷开发思想相悖,此时,

v(2,3)=R2+Da*R3-C2-C3/Da

v(1,2,3),即客户、本地团队、异地分布式团队三者均参与协作,即

v(1,2,3)=R2+E2+Da*(R3+E3)+c

对于异地分布式团队的地区优势分析,采用通过问卷调查[8]所得到的数据进行分析和计算。由于在问卷调查中仅得到一份关于目标一致性、学习能力、文化差异协调的回应,在此假设问卷调查结果可以接受,取Cronbachα系数的高可信度下限为0.7,设α0=0.7,εi=0.1,将α1=0.7,α2=0.76,α3=0.72,α4=0.61,α5=0.76;x1=4.75,x2=3.81,x3=3.74,x4=3.93,x5=3.7代入下式计算所需的结果。Da=α0+α1lnx1+α2lnx2+α3lnx3+

2.2特征函数的性质

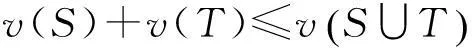
在团队协作博弈中,应追求博弈的超可加性,以获得最高开发效率和最大开发产出。

假设向量x∈Rn表示当参与人为N={1,2,…,n}时博弈x(N)的支付向量,xi表示团队参与人i∈N的协作产出,再给出如下的定义。

定义3如果对于∀i∈N,都有xi≥vi,则称博弈(N,v)的配置向量x∈RN符合个体理性。

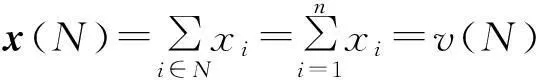
定义5如果对于∀i∈N,v(i)=0,则称合作博弈(N,v)是0-标准化的,如果对于∀i∈N,v(i)=0,且v(N)=1,则称合作博弈(N,v)是(0,1)标准化的。

2.3核心

在一个稳定的分配下,任何参与者都不会脱离这个联盟,因为脱离这个联盟会使该参与者的生产效率降低、收益减少。这些稳定的分配集称为核心,是合作博弈的一个主要解法。

假设向量x∈Rn表示当参与人为N={1,2,…,n}时博弈x(N)的支付向量,xi表示团队参与人i∈N的协作产出。

定义6(核心)通常将分配集

C(v)≡{x∈Rn|x(N)=v(N),且对于∀S∈2N，都有x(S)≥v(S)}称为核心。

由上面定义可以看出,核心不但要满足集体理性,还要满足个体理性。对于一个N人合作博弈(N,v),其分配集x(v)不被任何分配向量所占优,其全体称为核心,记为C(v)。

核心具有如下的特征:

1) 核心C(v)是分配集中的一个凸集;

2) 若核心C(v)不为空,将核心C(v)中的向量x作为分配,则x既满足个体理性也满足集体理性。

3) 用核心作为合作博弈的解,其最大缺陷是核心可能为空。

2.4核仁

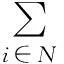
当核值存在时,核仁必包含在核中[9]。

当核心存在时,核仁是位于表示核心集合的区域的中心,故核仁具有如下性质:

1) 核仁满足个体理性和集体理性;故核仁的分配结果完全符合分配向量的要求。

2) 所有博弈问题有且仅有一个核仁,这表明了核仁的存在性及求解问题的意义。

3) 若核心存在,则核心与核仁重合,适用于博弈局中人不多时利用作图法求核仁。

下面给出一个核仁的具体算例。

根据核心的定义,本文模型中合作博弈的核心可定义为

={(x,1.627,1.192-x):0≤x≤1.577}根据核仁定义可知:

当S1={1}时,有e(S1,x)=0-x=-x;

当S2={2}时,有e(S2,x)=0-1.627=-1.627;

当S3={3}时,有e(S3,x)=0-(1.192-x)=

x-1.192;

当S4={1,2}时,有e(S4,x)=1.242-(x+

1.627)=-x-0.385;

当S5={1,3}时,有e(S5,x)=1.192-(x-x+1.192)=0;

当S6={2,3}时,有e(S6,x)=0.192-(1.627+1.192-x)=x-2.627;

当S7={1,2,3}时,有e(S7,x)=2.819-(x+

1.627+1.192-x)=0;

核仁的计算可通过求一系列线性规划来完成[10],这种求解方法虽然在理论上可行,但具体实现这一算法非常繁杂与费时,其计算复杂度为Ο(4n)[11],当n稍大时,其计算量难以接受。

2.5夏普利值

定义8博弈局中人采用合作博弈的形式进行利益分配,局中人i的夏普利值可按下式计算

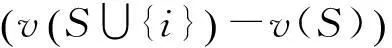
式中,s表示联盟S中的参与人个数,v(φ)=0。

故夏普利值恰好就是参与人i在联盟S中的边际贡献的期望得益。

设博弈局中人N={1,2,3},其中局中人1为客户,局中人2为本地团队,局中人3为异地分布式团队。博弈参与者形成的联盟如图2所示。

图2　3人合作博弈网格结构

根据夏普利值求解公式,根据博弈(N,v)的夏普利值将大联盟的产出v(N)按照公式进行分摊

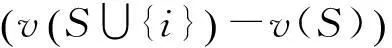
式中,s表示联盟S中参与人的个数,本模型中n=3;联盟s中没有其他参与人时,s=0,ν(0)=0;联盟s中有一个人参与时,s=1;联盟s中有2个人参与时,s=2;联盟s中有3个人参与即客户、本地团队、异地分布式团队三者均参与协作时,s=3;则客户、本地团队、异地分布式团队对项目进程的边际贡献为

同理可得

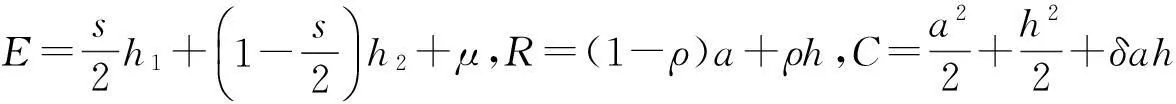
客户对项目进程的边际贡献为

本地团队对项目进程的边际贡献为

异地分布式团队对项目进程的边际贡献为

假设在团队初期,各团队均以自己任务为主,则团队用于自身工作任务的劳动为0.6,用于与其他团队进行协作的劳动为0.4,此时定义这2种劳动的互斥程度也以自身工作任务为主,则δ为0.6,在项目之初,假设各团队所承担任务的差异为0.5,取一个中间值,项目管理者的贡献系数也取中间值为0.5,团队协作效用比为0。即:

此时得出客户对项目进程的边际贡献为0.42，本地团队对项目进程的边际贡献为0.42，异地分布式团队对项目进程的边际贡献为0.29。

表1　团队协作夏普利值相关数据

3结论

针对异地分布式敏捷开发的团队协作容易受时差、文化差异、团队内外部以及客户价值等的影响，本文提出了一种改进的团队协作框架。并用博弈论的研究方法，通过核心，核仁揭示了合作各方为稳定的分配集，通过夏普利值分析进行了合作博弈的数值分配。分析结果表明，客户与本地团队对团队协作边际贡献较大，异地分布式团队对团队协作边际贡献较小。在未来相关研究中，我们会从异地分布式团队协作的任务分解等方面着手，完善队协作的研究。

参考文献：

[1]AnsgarL,JürgenM,DieterR.TowardsaMulti-CriteriaDevelopmentDistributionModel:AnAnalysisofExistingTaskDistributionApproaches[C]∥InternationalConferenceGlobalSoftwareEngineering, 2008: 109-118

[2]MaloneTW.ModelingCoordinationinOrganizationsandMarkets[J].ManagementScience, 1987, 33(10): 1317-1332

[3]Nguyen-DucA,CruzesDS,ConradiR.TheImpactofGlobalDispersiononCoordination,TeamPerformanceandSoftwareQuality:ASystematicLiteratureReview[J].InformationandSoftwareTechnology, 2015, 57: 277-294

[4]WireduGO.AFrameworkfortheAnalysisofCoordinationinGlobalSoftwareDevelopment[C]∥InternationalWorkshoponGlobalSoftwareDevelopmentforthePractitioner,Shanghai, 2006: 38-44

[5]黄武军, 刘天虎, 许维胜,等. N人合作博弈的Nash及演化均衡稳定策略分析[J]. 计算机工程与应用, 2010, 46(17): 11-14

HuangWujun,LiuTianhu,XuWeisheng,etal.StableStrategyAnalysisofNashandEvolutionaryEquilibriumBasedonN-PersonCooperativeGames[J].ComputerEngineeringandApplications, 2010, 46(17): 11-14 (inChinese)

[6]YinMing,LiuQi,ZhengZhanxing.TheInter-OrganizationalInformationSystemAdaptationMechanismBasedonOrganizationalIdentification[C]∥InternationalConferenceonSoftwareEngineeringandInformationSystem,Shijiazhuang,China, 2013: 9-10

[7]GregorS.TheNatureofTheoryinInformationSystems[J].MISQuarterly, 2006, 30(3): 611-642

[8]赵嵩正, 肖伟. 虚拟团队关键成功因素模型构建与实证研究[J]. 管理工程学报, 2006, 3(20): 89-93

ZhaoSongzheng,XiaoWei.ACriticalSuccessFactor(CSF)ModelofVirtualTeamDevelopmentandEmpiricalStudy[J].JournalofIndustrialEngineering/EngineeringManagement, 2006, 3(20): 89-93 (inChinese)

[9]FleuryC,FereyN,VezienJM,BourdotP.RemoteCollaborationAcrossHeterogeneousLargeInteractiveSpaces[C]∥IEEESecondVRInternationalWorkshoponCollaborativeVirtualEnvironments,Arles,France, 2015: 9-10

[10]JaakkolaH,HennoJ,ThalheimB,MakelaJ.Collaboration,DistributonandCulture-ChallengesforCommunication[C]∥InternationalConventiononInformationandCommunicationTechnology,ElectronicsandMicroelectronics,Singapore, 2015: 657-664

[11]QiangMa,MuthukrishnanS,ThompsonB,CormodeG.ModelingCollaborationinAcademia:AGameTheoreticApproach[C]∥InternationalWordWideWebConferenceSteeringCommittee,Geneva,Switzerland, 2014: 1177-1182

Study on Game Theory Research of Geographically Distributed Agile Software Team Coordination

Yin Ming1, Jiang Dan1, Ma Jing2, Deng Guolin1

1.School of Software and Microelectronics, Northwestern Polytechnical University, Xi′an 710072, China 2.Shanghai Aircraft Customer Service Company, Shanghai 200241, China

Abstract:In the process of distributed agile development , solving the problem of the agile collaboration is highly needed in order to achieve the offsite rapid response and feedback between all parties. For geographically distributed agile collaborative development process, we propose its improved framework of adaptive team collaboration. By employing cooperative game theory, we elaborate our work from the core, nucleolus, shapley value respectively. Core identifies the stable distribution set of each party which is geographically distributed, and the distribution results of the nucleolus is more difficult. Through mainly focusing on the shapley value analysis, we conduct the distribution of the shapley value of cooperative game. Data reveals that the marginal contribution from the customer and the local team is the greatest while that of the geographically distributed team is the smallest.

Keywords:geographically distributed; agile development ; teamwork; Game theory

收稿日期：2015-10-22

基金项目：国家自然科学基金(71201124)及西北工业大学研究生创意创新种子基金(Z2016193)资助

作者简介：殷茗(1978—)，女，西北工业大学副教授、博士，主要从事信息管理的研究。

中图分类号：TP311.5

文献标志码：A

文章编号:1000-2758(2016)04-0714-06