基于遗传算子采样的自适应代理优化算法
宋保维, 王新晶, 王鹏
(西北工业大学 航海学院, 陕西 西安 710072)
基于遗传算子采样的自适应代理优化算法
宋保维, 王新晶, 王鹏
(西北工业大学 航海学院, 陕西 西安710072)
摘要:提出一种应用于黑盒问题(black-box problem)的优化算法,称为遗传算子采样(genetic operator sampling,GOS)自适应代理优化算法。通过对当前样本进行两两交叉,对当前最优样本进行高斯变异2种算子获得候选样本集。对候选样本进行适应性评估,评估标准为候选样本处的交叉验证误差和该样本与父代样本之间最小距离的乘积,将乘积最大的样本加入已有样本集。GOS优化算法在一维问题中详细阐述,与有效全局优化算法(efficient global optimization,EGO)和最大化模型误差算法(maximum square error,MSE)在3个典型数学算例中进行对比,验证该算法的有效性。
关键词:代理模型;遗传算子;采样准则;代理优化
设计优化问题通常包含计算量大的高保真度模型(计算流体力学、有限元分析、基于试验的工程计算等)。由于目标函数与设计变量之间没有显式函数表达,这类问题称为黑盒问题。传统基于梯度的优化算法(牛顿法)和基于函数估计的优化算法(遗传算法)已经不适用于此类问题。代理模型作为一种有效的工具,为黑盒问题提供满足一定精度的合理近似。同时,在设计优化过程中,为了减小计算代价和过滤高保真度模型噪声,使用代理模型已经成为一种趋势。典型的代理模型包括多项式响应面(PRS)、克里金模型(KRG)、径向基函数(RBF)、支持向量回归模型(SVR)等。代理模型方法已经广泛应用于飞行器设计、汽车设计等领域。
基于代理模型的优化算法是依据少量初始样本建立代理模型,基于采样准则在设计空间增加样本并对代理模型进行更新,当模型精度满足要求时,对代理模型进行优化获得最优解的算法。代理优化算法从Jones等人提出有效全局优化算法(EGO)[1]开始,获得了广泛关注,并成功应用于相关工程设计优化[2-4]。此后,很多EGO改进算法[5-6]以及不同的自适应采样代理优化算法[7-10]被提出。有些方法在寻优过程中逐步提高代理模型整体精度,当迭代次数达到最大时对代理模型进行优化;有些方法在寻优过程中仅考虑最优解附近的局部区域,当确定最优解区域后重点对该区域进行寻优。大部分代理优化算法通过优化辅助函数获得新增样本。本文提出的优化算法的优势是不需要优化辅助函数,通过遗传算子获得候选样本集,通过采样准则获取新增样本,提高模型更新效率;同时该算法适用于各种代理模型,具有广泛适用性和稳定性。GOS算法与EGO、MSE算法进行对比,证明算法的有效性。
1基于GOS的自适应代理优化算法
1.1自适应采样方法
一种好的采样准则可以在全局空间探索和局部空间开发之间进行权衡。本文提出的采样准则的基本过程是建立样本交叉验证误差的代理模型;通过对已有样本进行两两交叉、对当前最优样本进行变异产生新的候选样本集,同时计算候选样本集中每个样本与已有样本的最小距离,交叉验证误差和最小距离的乘积作为评价候选样本适应性的准则,将乘积最高的候选样本作为新增样本。采样准则的基本思想是:在交叉验证误差较大处采样可以很好地提高代理模型的精度,计算候选样本与已有样本的最小距离可以避免样本聚集,二者的乘积是对设计空间探索和开发的一种权衡。
交叉验证(cross validation,CV)误差通常用来验证代理模型的精度。典型的leave one out cross validation(LOOCV)是取样本中的一个作为验证样本,剩下的样本用来建立代理模型。代理模型在验证样本处的预测值与该样本对应的真实值之间的误差即为该点处的交叉验证误差。如果样本较多,可以将样本分成K份,取K-1份含有的所有样本建立代理模型,剩下的一份样本作为验证样本,在验证样本处预测值与真实值之差即为该部分样本的交叉验证误差;重复执行K次即可得到所有样本的交叉验证误差。GOS优化算法使用交叉算子和变异算子产生候选样本集。样本采用十进制编码,避免使用二进制编码带来的编码解码过程。交叉算子采用中间重组算法(intermediate recombination,IR),这种杂交算法结合两父代样本的信息,在父代样本周围随机产生2个子代样本
(1)
式中,X和Y是父代样本,Z是子代样本,α代表[-1,1]之间随机选取的权重因子。每两个父代样本可以产生2个候选样本。考虑到样本数量的有限性,交叉操作对于所有样本两两进行,可以进行较大范围的样本探索。
高斯变异算子,是一种对重点区域局部搜索的变异算子。在进行变异操作时,用符合均值为m,方差为s2的正态分布的一个随机数代替原有的基因值。具体实现时,均值、方差的取值和变异位按(2)式处理
(2)
式中,xpbs是当前过程最优样本,umax和umin为设计变量上下限,ri是[0,1]之间的随机数,x′为变异后样本。变异算子只针对样本中的最优样本进行操作,保证了局部开发的特性。
候选样本的适应性评估采用下式进行
(3)
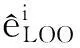
(4)
式中,Np代表每一代候选样本的数量。
为了防止新增样本的聚集,每隔5次(d≤3)或10次(d>3)采样进行1次优化运算。其中d为设计变量的数量。
1.2GOS优化算法流程
GOS优化算法的具体步骤为:
1) 采用OLHS(optimal latin hypercube sampling)试验设计方法在设计空间选取初始样本,并运行高保真度模型得到相应的响应值。
2) 基于样本及其响应值,构建代理模型。本文采用KRG方法建立代理模型,但是并不限于KRG模型。
3) 基于LOOCV得到样本处交叉验证误差,并用RBF建立交叉验证误差的代理模型。
4) 对所有样本进行两两交叉运算,对当前最好样本进行变异运算,得到候选样本集。
5) 根据(3)式计算所有候选样本适应度,将乘积最高的样本及其响应值加入已有样本空间并更新代理模型。
6) 重复步骤2)~步骤5)5或10次后进行基于代理模型的优化得到当前最优解,将最优解及其响应值加入样本空间。
7) 若满足收敛准则,优化停止;否则执行步骤2),进行下一轮迭代。本文的收敛准则为预先设定的总的函数估计量。
2GOS优化算法举例与验证
采用1-D测试函数对GOS优化算法进行阐述。GOS与MSE和EGO算法在3个测试函数中进行对比以验证其有效性。EGO算法是以KRG模型为代理模型的优化算法,通过优化辅助函数(excepted improvement,EI)自适应采样求得最优解。MSE算法是在以KRG为代理模型的优化算法中,在预测方差最大处进行采样的一种优化算法。
2.1测试函数和试验设定
1-D函数、Branin函数、Hartman3和Hartman6函数4个广泛应用的函数作为测试函数。它们的数学表达为:
1-D函数
(5)
Branin函数
(6)
Hartman3和Hartman6函数
(7)
式中,a=[1 1.2 3 3.2]。当含有3个变量时,矩阵b和d为

当含有6个变量时,矩阵b和d为

d=
表1 测试函数的数值设定
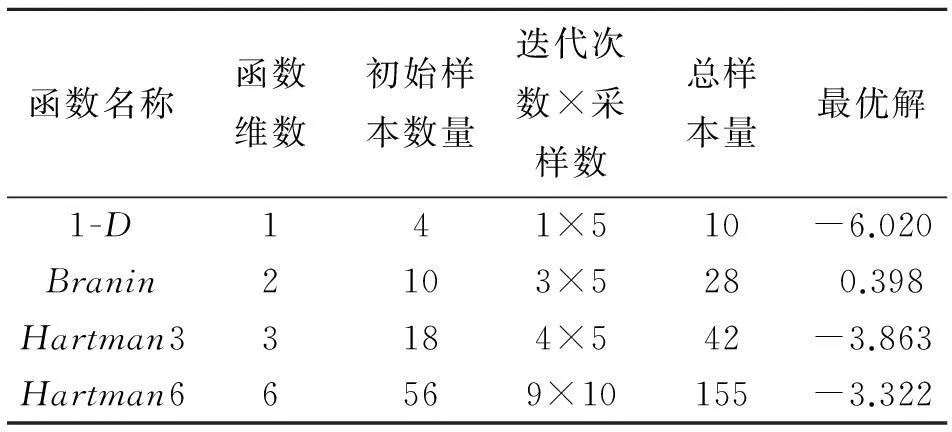
函数名称函数维数初始样本数量迭代次数×采样数总样本量最优解1-D141×510-6.020Branin2103×5280.398Hartman33184×542-3.863Hartman66569×10155-3.322
表1给出了4个测试函数的基本信息,为了避免试验设计结果的偶然性,对每个测试函数进行30次优化计算,采用30次计算结果的平均值进行比较。采用遗传算法(GA)对代理模型进行优化。由于本文设定的收敛准则为预先设定的函数估计量,所以算法优劣的判定标准为:在相同函数估计量前提下,优化结果更接近最优解的算法更好。KRG模型通过Lophaven等人[11]开发的KRG工具箱获得,交叉验证、EGO算法通过Viana等人[12]开发的SURROGATESToolbox工具箱获得。
2.2GOS算法在1-D函数的优化过程
图1给出了GOS算法在1-D函数的优化过程。
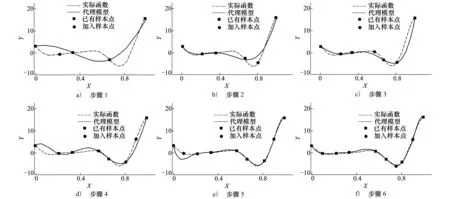
图1 GOS算法在1-D函数的优化过程
图中虚线表示真实函数,实线表示使用已有样本(方形)建立的代理模型,圆形表示本次迭代过程获取的新增样本。初始样本为[0,0.333,0.666,1],5次迭代过程加入样本分别是[0.213,0.810,0.568,0.902,0.089]。从图中可以看出在5次采样之后,代理模型与实际模型已经相当吻合,使用GA优化算法在图1e)中找到的最优解为0.759,响应值为-6.019,与实际结果符合。
2.3GOS与MSE、EGO、OLHS算法的比较
图2给出了GOS、MSE、EGO、OLHS 4种优化算法对Branin函数优化时样本分布情况。其中前3种都是自适应采样优化算法,第4种是基于OLHS方法一步采样然后对代理模型进行优化。Branin函数含有3个全局最优,算法找到一个即认为找到最优解。圆点表示样本,星号表示算法得到的最优解。从计算结果来看,4种算法获得最优解需要的函数估计次数只有22、22、23和28,都比设定的28次要少。GOS算法的样本分布均匀,没有在非最优解的区域(左下、右上)进行采样;MSE算法注重在边界处进行采样,在边界精度满足要求的情况下,开始向内部采样(从左下角开始)并逐步找到最优解。EGO算法注重于EI的提升,样本在最优解附近聚集,此时收敛到最优解处需要较多迭代数;OLHS算法属于一步采样算法,样本数量预先设定,其空间填充特性最好,但是优化精度却不是最高。总体来说,4种算法都以较少的样本找到最优解。与一步采样算法(OLHS)相比,3种自适应采样算法效果更好。
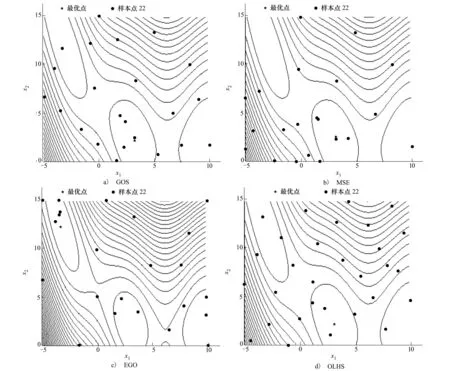
图2 GOS、MSE、EGO和OLHS算法对Branin函数优化时的样本分布情况
图3给出GOS、MSE和EGO 3种算法对Branin、Hartman3和Hartman6函数的优化过程。每一迭代处的最优解是30次计算的平均值。从Branin函数看,MSE算法表现最好,拥有较快的优化效率;GOS算法表现与MSE算法几乎相同,EGO算法在较少的迭代过程中不能迅速地收敛到最优值,优化结果与图2结果吻合。在Hartman3函数优化过程中,GOS算法表现最好,在设定的最大样本量处得到最好的结果;EGO算法在优化初期效果比较明显,在优化后期寻优速度减慢,优化结果与MSE算法相近。在Hartman6函数的优化过程中,EGO算法优势比较明显,不仅在采样初期找到最优解,而且寻优速度最快;MSE算法效果最差;GOS算法介于两者之间,但是当样本数量达到设定值时,其优化结果与EGO结果相差不大。
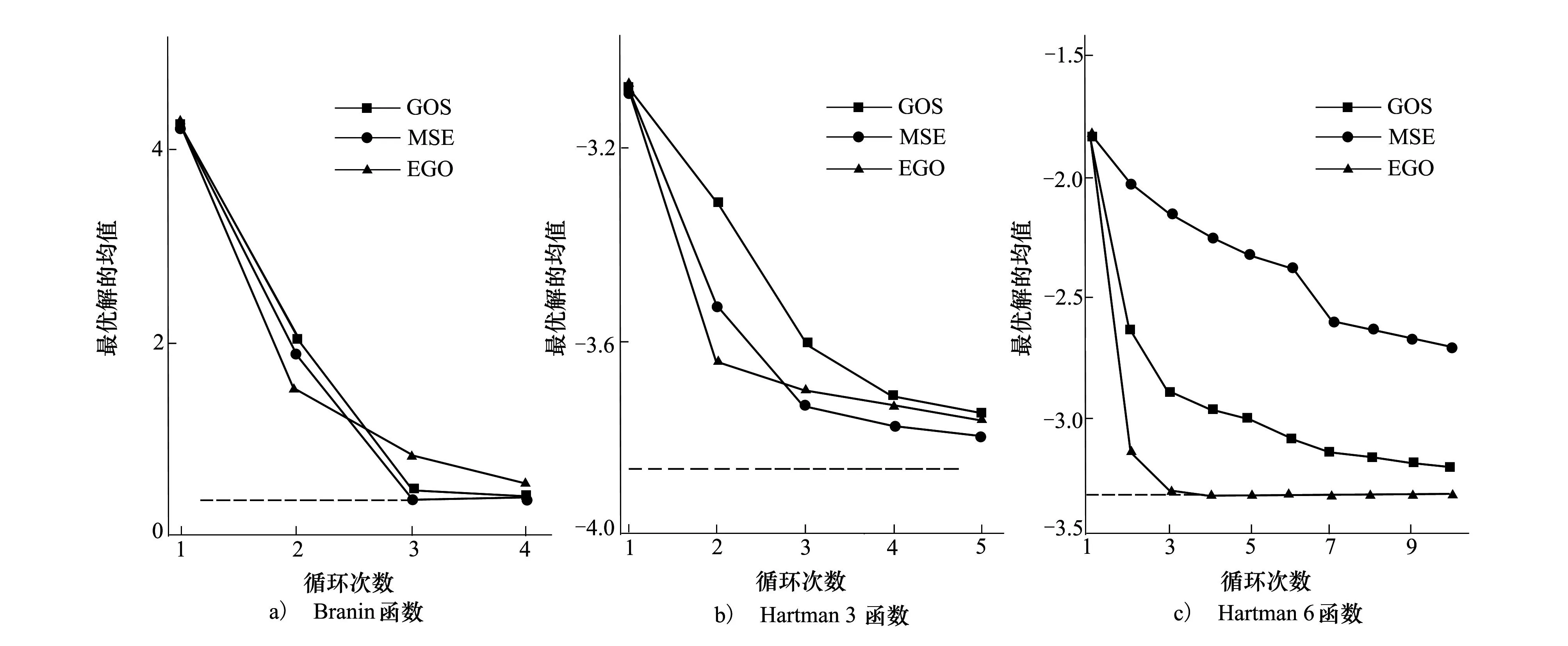
图3 GOS、MSE和EGO算法对3个测试函数的优化过程
图4给出GOS、MSE、EGO、OLHS 4种算法对3个测试函数优化结果的箱体图。箱体图得出的结论与图3相似。GOS算法对Hartman3函数优化结果最好,MSE算法对Branin函数优化结果最好,EGO算法对Hartman6函数优化结果最好。从图中还可以看出,除了低维函数(Branin) 中OLHS算法结果比较好外,在高维函数中其优化结果都是最差的,这也说明自适应采样代理优化算法要好于一步代理优化算法。另外,GOS算法在3种测试函数中即使不是最好的,也是第2好的;而且从箱体图厚度可以看出,GOS算法的结果也是比较稳定的,对初始样本分布的依赖较小。
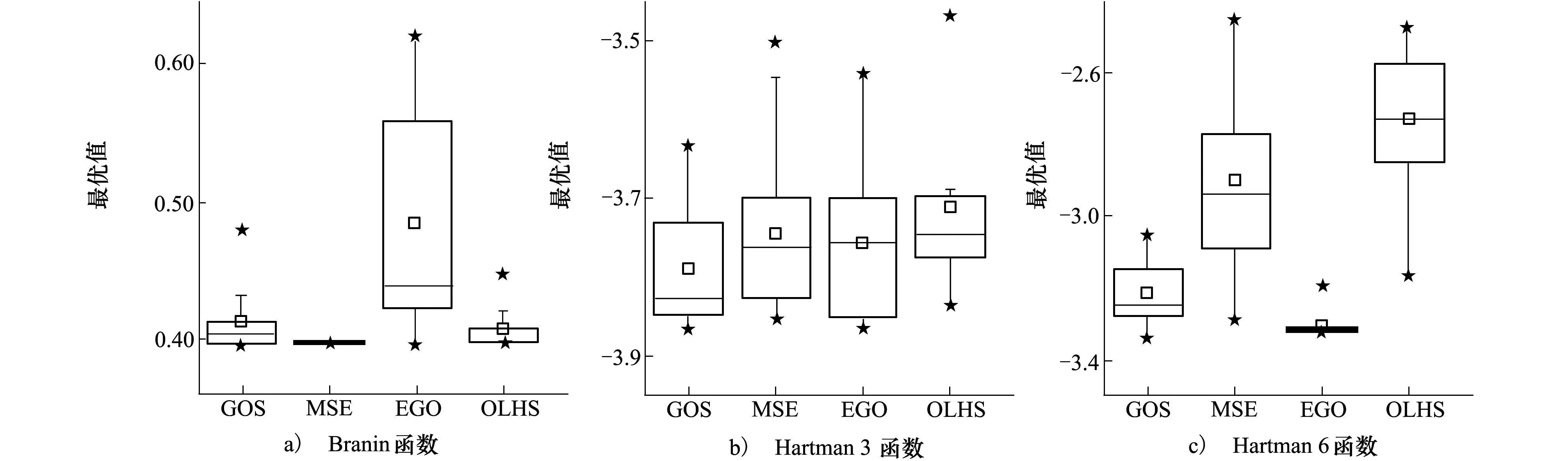
图4 GOS、MSE、EGO和OLHS算法得到测试函数最优结果的箱体图
3结论
本文提出一种优化算法,称为遗传算子采样(GOS)的自适应代理优化算法。该算法通过对所有样本进行交叉运算,对最优解进行变异2种算子产生候选样本集。基于提出的采样评估标准,对候选样本适应性进行评估,该评估标准能够很好地在减小模型误差和避免样本聚集2个问题中权衡。新增样本的获得不需要通过对辅助函数优化,提高了优化效率。GOS算法在1-D函数中进行了阐述,在3个测试函数中与MSE、EGO、OLHS算法进行对比。结果显示:
①自适应采样代理优化算法比一步采样代理优化算法更好,因为自适应采样算法考虑了模型的信息,可以更有针对性地更新代理模型;
②GOS算法能够在有限的函数估计下获得较好的优化结果;在测试函数中它即使不是最好的算法,也是第2好的算法;
③由于避免采用优化的方法获得新增样本,GOS算法大大提高了代理模型的更新效率;
④GOS算法比较稳定,对初始样本分布情况依赖较小。
参考文献:
[1]Jones D R, Schonlau M, Welch W J. Efficient Global Optimization of Expensive Black-Box Functions[J]. Journal of Global Optimization, 1998, 13(4): 455-492
[2]赵敏, 操安喜, 苟鹏, 等. 高效优化算法在船舶力学中的应用研究[J]. 船舶力学, 2008, 12(3): 473-482
Zhao Min, Cao Anxi, Gou Peng, et al. Application of Efficient Global Optimization in Ship Mechanics[J]. Journal of Ship Mechanics, 2008, 12(3): 473-482 (in Chinese)
[3]Lei G. Sequential Optimization Method for the Design of Electromagnetic Device[J]. IEEE Trans on Magnetics, 2008, 44(11): 3217-3220
[4]邓枫, 覃宁, 伍贻兆. EGO方法的训练算法及应用[J]. 计算物理, 2012, 29(3): 326-332
Deng Feng, Qin Ning, Wu Yizhao. Training Algorithms for EGO Method and Applications[J]. Chinese Journal of Computational Physics, 2012, 29(3): 326-332 (in Chinese)
[5]邹林君, 吴义忠, 毛虎平. Kriging模型的增量构造及其在全局优化中的应用[J]. 计算机辅助设计与图形学学报, 2011, 23(4): 649-655
Zou Linjun, Wu Yizhong, Mao Huping. Incremental Kriging Model Rebuilding Method and Its Application in Efficient Global Optimization[J]. Journal of Computer-Aided Design and Computer Graphics, 2011, 23(4): 649-655 (in Chinese)
[6]冯敏, 张建同. 基于改进Kriging模型的EGO算法的EI函数研究[C]∥第十届中国不确定系统年会, 2012
Feng Min, Zhang Jiantong. Expected Improvement in Efficient Global Optimization based on Bootstrapped Kriging[C]∥The tenth China Annual Conference on Uncertainty, 2012 (in Chinese)
[7]Huang D, Allen T T, Notz W I, et al. Global Optimization of Stochastic Black-Box Systems via Sequential Kriging Meta-Models[J]. Journal of Global Optimization, 2006, 34(3): 441-466
[8]Mehmani A. Surrogate-Based Design Optimization with Adaptive Sequential Sampling[C]∥53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 2012
[9]高月华, 王希诚. 基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学, 2012, 29(4): 90-95
Gao Yuehua, Wang Xicheng. A Sequential Optimization Method with Multi-Point Sampling Criterion Based on Kriging Surrogate Model[J]. Engineering Mechanics, 2012, 29(4): 90-95 (in Chinese)
[10] Viana F A, Haftka R T, Watson L T. Efficient Global Optimization Algorithm Assisted by Multiple Surrogate Techniques[J]. Journal of Global Optimization, 2013, 56(2): 669-689
[11] Lophaven S N, Nielsen H B, Søndergaard J. DACE-A Matlab Kriging Toolbox[EB/OL]. (2002-8-1)[2015-10-22].http:∥www2.imm.dtu.dk/~hbn/dace/.
[12] Viana F A C. SURROGATES Toolbox User′s Guide[EB/OL]. [2015-10-22].http:∥sites.google.com/site/felipeacviana/surrogatestoolbox.
An Adaptive Surrogate-Based Optimization Algorithm Assisted by Genetic Operators Sampling
Song Baowei, Wang Xinjing, Wang Peng
(School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:This paper proposes an optimization algorithm that is applied to Black-box Problem, called Genetic Operator Sampling (GOS) adaptive surrogate-based optimization algorithm. Genetic operators produce candidate sample set. Cross-over operator is executed between any two of samples and mutation operator is executed only on present best sample. Then an assessment criterion, which is the product of the cross validation error of the candidate sample and the minimum distance between it and existing samples, is used to judge the adaptation of each sample. The candidate sample with largest product will be added to existing samples. GOS is illustrated on 1-D function in detail and is compared to EGO and MSE algorithm on three typical functions, the results validated the effectiveness of GOS algorithm.
Keywords:surrogate model; genetic operators; sampling criterion; surrogate-based optimization
收稿日期:2015-10-22
基金项目:国家自然科学基金(51375389)资助
作者简介:宋保维(1963—),西北工业大学教授、博士生导师,主要从事水下航行器设计及多学科设计优化等研究。
中图分类号:TP18
文献标志码:A
文章编号:1000-2758(2016)04-0614-07

