加权期望残差极小化方法求解一类随机混合变分不等式

沙明娥

(昆明学院数学系，云南昆明650214)

加权期望残差极小化方法求解一类随机混合变分不等式

沙明娥

(昆明学院数学系，云南昆明650214)

考虑有限维空间中的一类随机混合变分不等式，将求解随机混合变分不等式转化为加权期望残差极小化模型，并在一定条件下，通过拟蒙特卡洛方法得到了加权期望残差极小化模型的解．

随机混合变分不等式;加权期望残差极小化模型;拟蒙特卡洛方法

1 预备知识

有限维空间中的混合变分不等式被广泛应用于实际问题之中．经济数学中的某些均衡问题、物理中的弹性力学问题等都可以在一定条件下转化为混合变分不等式加以研究．就实际问题而言，系统往往会受到随机因素的干扰，为了更好的描述实际问题，有必要研究随机混合变分不等式．假定(Ω，F，P)是一概率空间，F:Rn×Ω→Rn和f:Rn× Ω→R是两函数，K∈Rn是一非空闭凸集．随机混合变分不等式可以表述为:找x∈K满足

或等价表示为

其中a．s．表示在概率P下几乎必然成立．

近年来，许多研究者研究了类似的问题，例如，X．J．Chen等［1］研究了随机线性相补问题，并用期望残差极小化方法求解了随机线性相补问题;C．Zhang等［2］用期望残差极小化方法求解了随机非线性相补问题;M．J．Luo等［3］将期望残余极小化方法运用于随机变分不等式，并用该方法求解了随机变分不等式问题;H．Q．Ma等［4］研究了随机拟变分不等式问题，并用期望残差极小化方法求解了该问题，其他研究工作可参见文献［5－12］．

另一方面，由于期望残差极小化模型具有解不稳定，可能会出现多解情况等缺点，F．Liu等［13］改进了期望残差极小化方法，采用加权期望残余法求解了随机变分不等式问题．受以上工作启发，本文用加权期望残余法求解随机混合变分不等式问题，并用拟蒙特卡洛方法给出了该问题的解．

假定(Ω，F，P)是一概率空间，记E(·)为在概率P下的期望，‖·‖表示Rn空间的欧几里得范数，F:Rn×Ω→Rn和f:Rn×Ω→R是两函数，K∈Rn是一非空闭凸集．

首先给出本文将用到的一些假设和引理．

(A)对于x∈K，

(B)对于ω∈Ω;x，y∈K，

(C)对于ω∈Ω;x，y∈K，

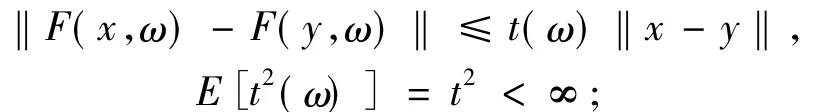
(D)对于ω∈Ω;x，y∈K，

(E)对于ω∈Ω;x，y∈K，

引理1．1［14］如果在Ω上可积，那么

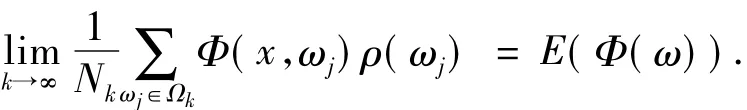
引理1．2［12］若函数 F1:Rn×ω→Rn1×n1，F2: Rn×ω→Rn1，xk∈Rn．当k→∞时xk→x*．假设对于，以下式子成立

那么以下结论成立:

定义

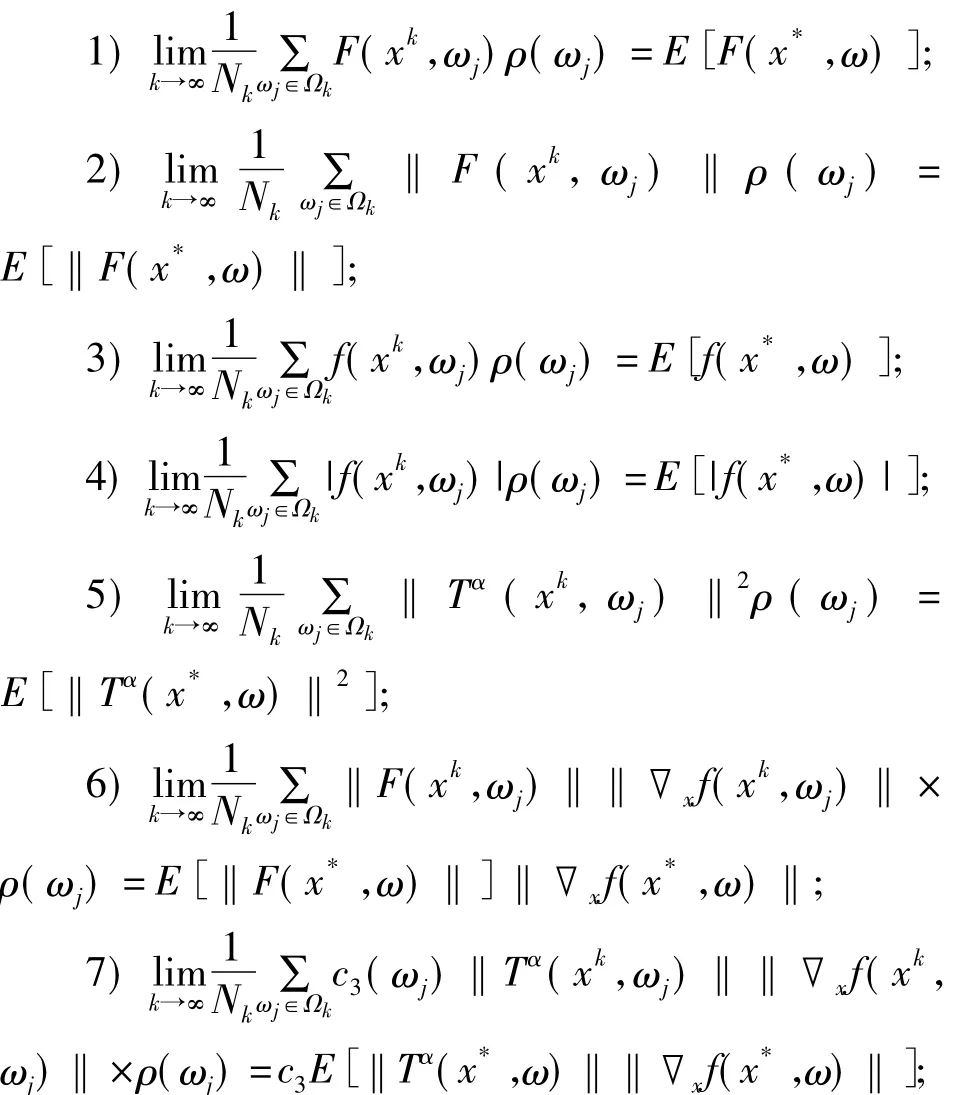
引理1．4［15］假定是非空闭集，是一开子集，f:Rn×U→R是一连续函数，其梯度fu(·，·)也是连续的．如果对于任意给定的u∈

在给出本文的主要结果之前，首先给出水平集和混合变分不等式MVI(E［F］，E［f］)的定义．对于任意的非负数c有:

混合变分不等式MVI(E［F］，E［f］)可以表述为:找x*∈K，满足

引理1．5 如果F和f满足假设(A)～(E)，那么混合变分不等式MVI(E［F］，E［f］)有唯一解x*∈K．

2 主要结果

定义函数如下

加权期望残余极小化法可以表述为求解下面的优化问题

其中，1＞a＞0为权重，ρ:Ω→［0，∞)是概率密度函数，并且

由引理1．4并结合文献［12］中的证明方法，很容易验证下面定理成立．

定理2．1 如果对于任意的Ω∈Ω，F(x，ω)关于x连续，f(x，ω)关于x是连续可微真凸函数，那么

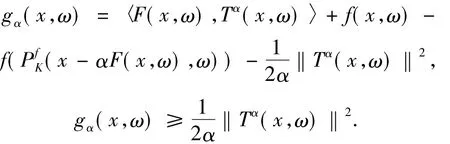
进一步，如果对于任意的Ω∈Ω，F(x，ω)关于x连续可微的，那么gα也是连续可微，并且有

对于问题(4)，将用拟蒙特卡洛法去求解．

令Ωk={ωj|j=1，2，…，Nk}为一列观测集，并满足Ωk∈Ω，当k→∞时，Nk→∞．对于每一个k，定义

考查下面的优化问题

记优化问题(4)和(6)的解集为S*和

证明 由引理1．5知存在x*∈K是混合变分不等式MVI(E［F］，E［f］)的解，即满足

由引理1．1和1．3知

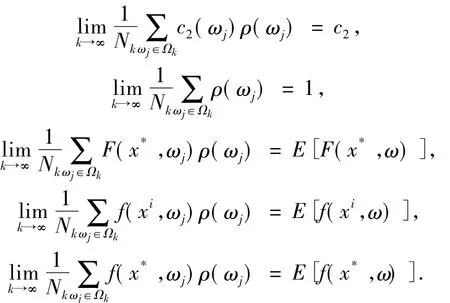
取整数，那么存在正整数k0＞0满足:对于任意的k＞k0有下列式子成立:

现令k＞k0，假定存在 珋c＞0，使得水平集无界，那么存在满足

因为

和

所以

又因为

并且当i→∞时，‖xi－x*‖∞，所以∞．这与Θk(xi)≤珋c矛盾．对于足够大的显然是非空有界的．

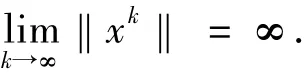
由引理1．5知存在x*∈K，从而有

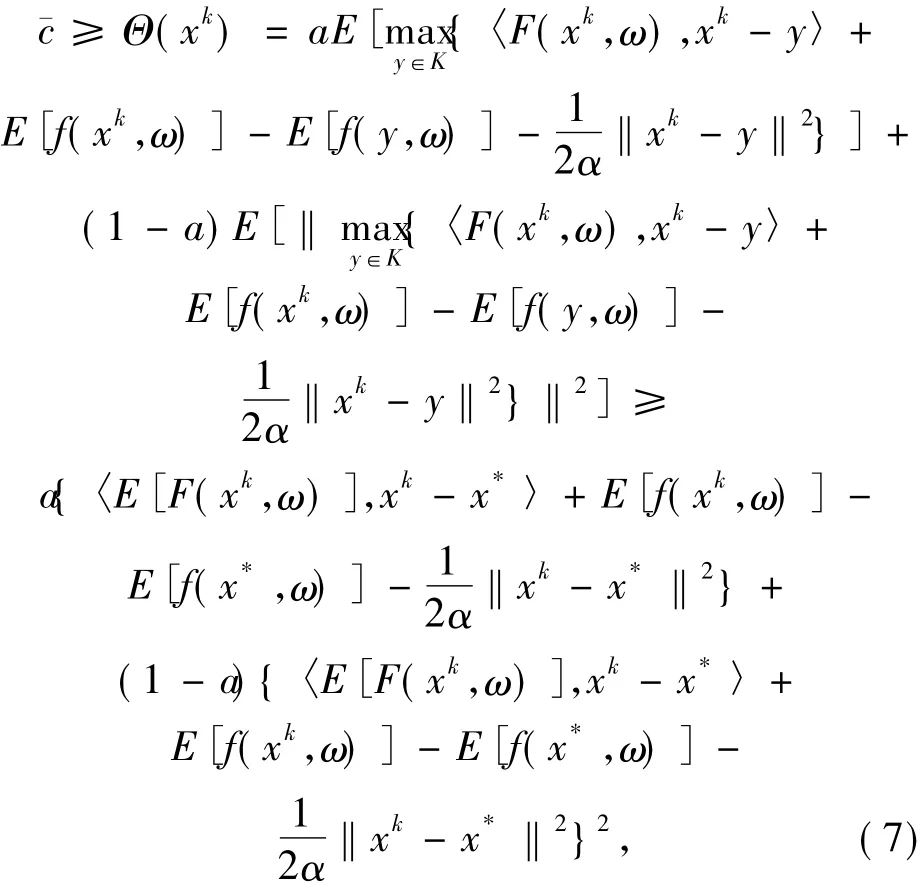
又因为

由(7)和(8)式知

因为

所以当k→∞时，Θ(xk)→∞，这与的定义相矛盾．所以对于任意的非负数有界．

下面的定理表明，最优问题(6)的每一个聚点都在S*中．

定理2．4 如果F和f满足假设(A)～(E)，对于足够大的，那么{xk}的每一个聚点都在S*中．

和

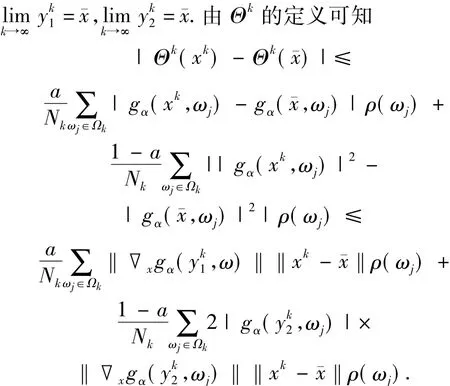
由定理2．1可知，对于任意的x，ω∈Ω有

从而可知

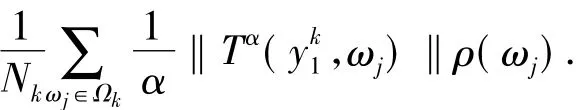
因为xk→珋x，由引理1．3知

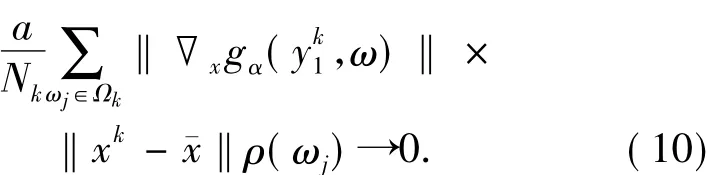
另一方面，由于对于任意的x∈K，ω∈Ω有

进而可知

由引理1．3知

由(10)和(11)式可知

值得注意的是

由引理1．1可知

参考文献

［1］CHEN X J，FUKUSHIMA M．Expected residual minimization method for stochastic linear complementarity problems［J］．Math Operations Research，2005，30:1022－1038．

［2］ ZHANG C，CHEN X J．Stochastic nonlinear complementarity problem and applications to traffic equilibrium under uncertainty［J］．J Optim Theory Appl，2008，137:277－295．

［3］LUO M J，LIN G H．Expectted residual minimization method for stochastic variational inequality problems［J］．J Optim Theory Appl，2009，140:103－116．

［4］MA H Q，HUANG N J．Expected residual minimization method for a class of stochastic quasivariational inequality problens［J］．J Appl Math，2012，2012:doi:10．1155/2012/816528．

［5］CHEN X J，WETS J B，ZHANG Y F．Stochastic variational inequalities:residual minimization smoothing sample average approximations［J］．SIAM J Optim，2012，22:649－673．

［6］FANG H，CHEN X J，FUKUSHIMA M．Stochastic R0matrix linear complementarity problems［J］．SIAM J Optim，2007，18:482－506．

［7］CHEN X J，ZHANG C，FUKUSHIMA M．Robust solution of monotone stochastic linear complementarity problems［J］．Math Programming，2009，117:51－80．

［8］JANG H，XU H．Stochastic approximation approaches to the stochastic variational inequality problems［J］．IEEE Trans Automat Control，2008，53:1462－1475．

［9］LIN G H，FUKUSHIMA M．New reformulations for stochastic nonlinear compelementarity problems［J］．Optim Methods and Software，2006，21:551－564．

［10］LUO M J，LIN G H．Convergence results of the ERM method for nonlinear stochastic variational problems［J］．J Optim Theory Appl，2009，142:569－581．

［11］LUO M J，LIN G H．Stochastic variational inequality problems with additional constraints and their applications in supply chain network equilibria［J］．Pacific J Optim，2011，7:263－279．

［12］MA H Q，WU M，HUANG N J，et al．Expected residual minimization method for stochastic variational inequality problem with nonlinear perturbations［J］．Appl Math Comput，2013，219:6256－6267．

［13］LU F，LI S J．Method of weighted expected residual for solving stochastic variational inequality problems［J］．Appl Math Comput，2015，269:651－663．

［14］PATRICK B．Probability and Measure［M］．New York:Wiley Interscience，1995．

［15］AUSLENDER A．Optimisation Methods Numeriques［M］．Paris:Masson，1976．

［16］MA H Q，HUANG N J，WU M，et al．A new gap function for vector variational inequalities with an application［J］．J Appl Math，2013，2013:doi:10．1155/2013/423040．

Weighted Expected Survival Minimization Method for Solving a Class of Stochastic Mixed Variational Inequality

SHA Ming’e

(Department of Mathematics，Kunming College，Kunming 650214，Yunnan)

In this paper，we consider a class of stochastic mixed variational inequalities in finite dimensional spaces．We solve stochastic mixed variational inequalities by weighted expected survival minimization method．Using the quasi-Monte Carlo method，we give the solution of weighted expected survival minimization method under some suitable conditions．

stochastic mixed variational inequality;weighted expected survival minimization method;quasi-Monte Carlo method

O176．31

A

1001－8395(2016)04－0536－06

10．3969/j．issn．1001－8395．2016．04．014

(编辑 李德华)

2015－12－01

国家自然科学基金(51402138)

沙明娥(1963—)，女，讲师，主要从事数学分析与应用模型的研究，E－mail:MingE－Sha@126．com

2010 MSC:65K10