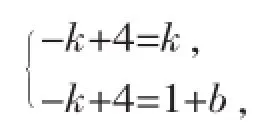直线与双曲线的相交问题——教材原题变式拓展（一）

蒋丽亚



思维训练营/例题延伸

直线与双曲线的相交问题
——教材原题变式拓展（一）

蒋丽亚

课本例题和习题是同学们理解、掌握知识的载体，数学课堂教学中，教师可以根据学习目标和同学们交流反馈的信息精选题目，并通过变式训练让同学们在解答探索过程中深化对知识的理解和应用.下面我们以“反比例函数”这一章中的一道课本习题为例，对它进行一些变式探究，来解决直线与双曲线的交点问题.

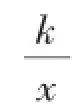
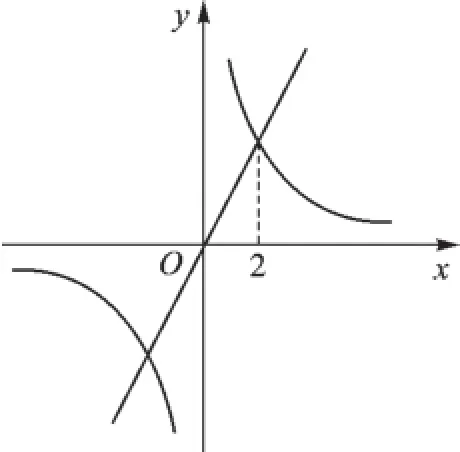
（1）求k的值，并画出这个反比例函数的图像；

（2）根据反比例函数的图像，指出当-4< x<-1时，y的取值范围.

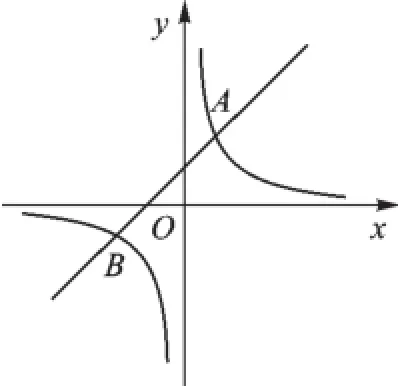
【思路点拨】这是直线与双曲线相交的计算问题，解决问题的关键是图像的交点同时满足两个函数解析式，把x=2代入正比例函数y=2x，求出纵坐标y=4，代入反比例函数，即可求出k的值.再结合图1，求出-4< x<-1时，y的取值范围是-8

图1

（1）试确定这两个函数的表达式；

（2）求出这两个函数图像的另一个交点B的坐标，并根据图像写出使反比例函数的值大于一次函数的值的x的取值范围.

图2

【思路点拨】可以把A（1，-k+4）分别代入两个函数关系式中，得到关于k、b的二元一次方程组，求出两个函数表达式.联立方程组，求出交点B的坐标，再根据图像得到反比例函数的值大于一次函数的值的x的取值范围.

【说明】变式1的两个函数和点A的坐标都含有两个不同的参数，问题的关键是把点A的坐标代入两个表达式，联立方程组，求出这两个参数.这里需要解两个不同的二元一次方程组，求表达式时是解关于参数k、b的方程组，求交点坐标时是解关于x、y的方程组，两者要区别开来.

（1）求反比例函数的解析式；

（2）若直线y=x+b与反比例函数的图像只有一个公共点，求b的值.

又∵因为直线经过一、三、四象限，

【说明】把变式2的反比例函数和一次函数两个表达式联立方程组，含有参数b，这里需要根据方程根的判别式与交点个数的关系求出参数b的值.

【思路点拨】先根据不等式组求出a的取值范围，再把一次函数和反比例函数的表达式联立方程组，根据a的取值范围判断根的判别式的情况，从而得出公共点的个数.

∵因为-2

以上三个变式都是围绕直线与双曲线的交点情况展开，由简单到复杂，由确定到不确定.同学们解决这类问题的关键是把两个函数表达式联立方程组，由根的判别式和交点个数的关系解决问题.再结合已有的知识和数学思想方法灵活应用，如方程、不等式、分类思想、转化思想，从而解决各类直线与双曲线的交点问题.

作者单位：（江苏省常州市武进区前黄实验学校）