变质量动力吸振器瞬态减振性能研究

赵艳青，宋伟志，孙　丽,包海涛

(1.淮阴工学院 交通工程学院，江苏 淮安 223003；2.洛阳理工学院 机械系，河南 洛阳 471000)



变质量动力吸振器瞬态减振性能研究

赵艳青1，宋伟志2，孙丽1,包海涛1

(1.淮阴工学院 交通工程学院，江苏 淮安 223003；2.洛阳理工学院 机械系，河南 洛阳 471000)

摘要：为确定变质量动力吸振器的瞬态减振性能以及质量变化快慢对瞬态减振性能的影响，利用Matlab仿真方法对吸振器变质量吸振过程进行分析，讨论质量变化快慢对瞬态减振效果的影响，并分析两种质量变化过程瞬态减振效果不同的原因。结果表明：吸振器质量增加过程，主系统加速度响应随着质量的增加先增加后减小；吸振器质量减少过程，主系统加速度随着质量的减少而减小。

关键词：动力吸振器；变质量；瞬态减振；Matlab仿真

0引言

机械设备在工作过程中常伴有振动现象，振动不但影响其工作性能，而且可能会造成零部件损坏，因此，振动控制技术研究越来越引起人们的重视。动力吸振技术是工程中常用的减振手段[1]。但是，动力吸振器(Dynamic Vibration Absorber)一经设计，系统参数将固定不变，当外界激振频率偏离其固有频率时，减振性能因失谐而急剧变差。为了拓宽DVA的减振频带，研究人员提出了自适应动力吸振器(Adaptive Dynamic Vibration Absorber, ADVA)。ADVA能够实时调整自身参数使其固有频率追踪外界激振频率的变化，从而在较宽频带内抑制主系统振动，克服了DVA减振频带过窄的缺点[2]。ADVA由于具有结构简单，耗能低，稳定性好，有效减振频带宽等优点，因此在工程实践中得到广泛应用[3-4]。

目前，许多文献对ADVA进行了报道[5-12]。长安大学高强设计了一种新型的变质量动力吸振器(Variable Mass Dynamic Vibration Absorber，VM DVA)并对其稳态减振性能进行分析[12]。该吸振器利用小瓶和质量块作为吸振器固定质量，小瓶内的液体作为可变质量介质，通过向小瓶内注入或者从小瓶中抽出一定量的液体改变吸振器质量，从而调节吸振器固有频率追踪外界激振频率的变化，拓宽了有效减振频带。为了研究变质量动力吸振器的瞬态减振性能以及质量变化率对瞬态减振性能的影响，本文通过仿真对变质量动力吸振器的瞬态减振过程进行探讨，力图为变质量控制方法的研究提供参考依据。

1变质量动力吸振器宽频减振原理

变质量动力吸振器模型如图1所示。

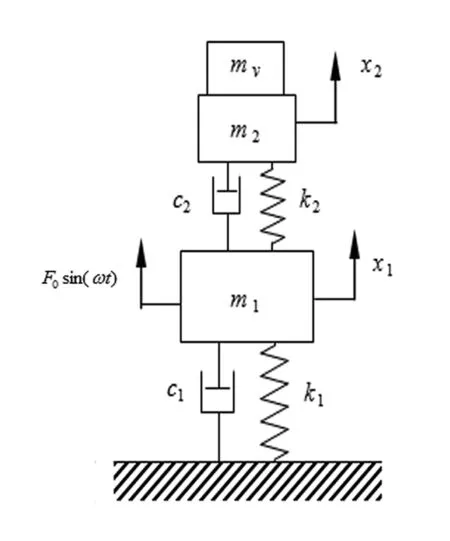
图1变质量动力吸振器模型

模型忽略了质量变化对系统阻尼的影响，利用牛顿第二定律可得主系统——变质量动力吸振器系统运动微分方程组为：

(1)

吸振器可变质量mv在0到mvmax范围内连续变化时，吸振器总质量则在m2与m2+mvmax之间连续变化。由于自适应动力吸振器阻尼往往较小，这里忽略阻尼c2的影响，变质量动力吸振器固有频率可表示为

(2)

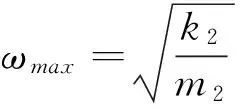
2变质量动力吸振器仿真研究

为了分析变质量动力吸振器的瞬态减振性能和质量变化快慢对减振性能的影响，利用Matlab软件对图1所示模型进行仿真研究，模型参数如表1所示。

表1　变质量动力吸振器系统参数

当吸振器可变质量取最小值mvmin=0g和最大值mvmax=10g时，主系统幅频响应函数如图2所示(——表示mv=20g；—·— 表示mv=0g)。从图中可以看出，两种情况下吸振器分别在14.06Hz和11.48Hz处获得最佳减振效果。

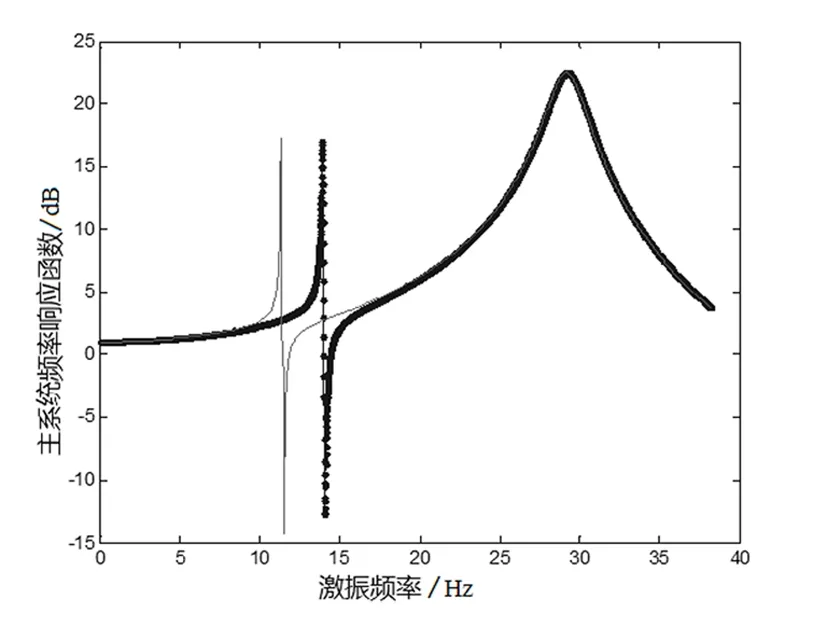
图2主系统幅频响应函数

为了研究吸振器质量变化对其瞬态减振性能的影响，将质量变化分两种情况：质量增加和质量减小。针对质量增加情况：设置外界激振力幅值F0=4N、频率ω=11.48Hz，仿真方法选用Newmark算法家族中的平均加速度法(γ=0.5，β=0.25)，仿真步长选为0.001s，仿真时间选为70s。设置激振频率为11.48Hz，吸振器可变质量由0g匀速增加到10g，质量增加的三组具体变化过程如下式所示。

(3)

(4)

(5)

由式(3)～(5)可看出，三组变化过程的吸振器可变质量在前10s均为0g，从第10s开始吸振器可变质量由0g逐渐增到10g，所用时间分别为3s、6s和9s。质量增加过程的主系统加速度时域响应如图3所示。

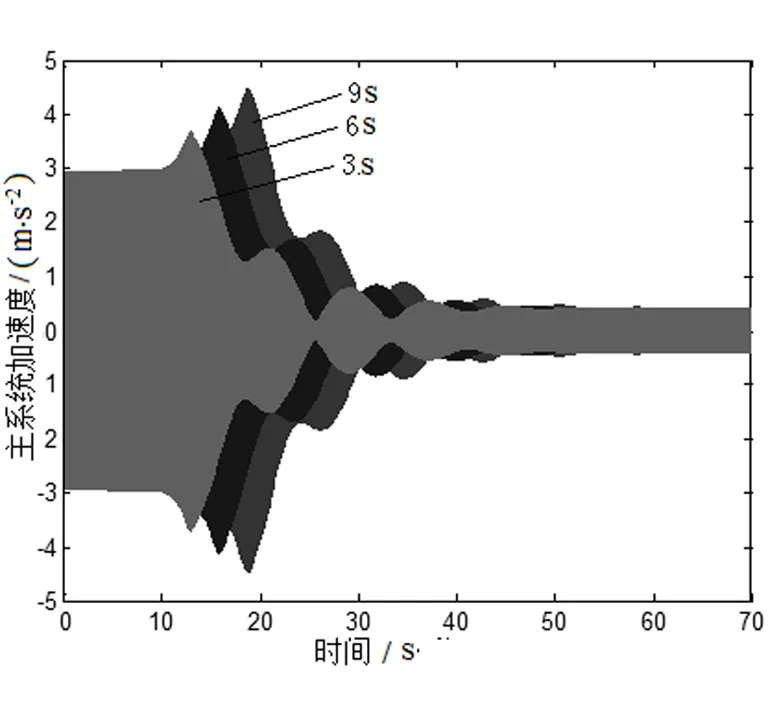
图3主系统加速度时域响应

从图3中可看出，质量变化时间为3s、6s、9s时，主系统加速度时域响应都随着质量的增加先增加后减小，其中最大增加量分别为24.2%、38.7%、50.5%，且最终均减为原来的14.2%。针对这种现象出现的原因，现利用可变质量为0g、3g、5g、7g、9g、9.2g、9.5g、10g时的幅频响应函数在11.48Hz处的响应值进行说明，该八组响应值如表2所示。从表中可以看出：在11.48Hz处的主系统频率响应值随着可变质量的增加先增加后减小。质量增加过程中，吸振器固有频率需越过共振区，因此，主系统加速度响应随着质量的增加先增加后减小。

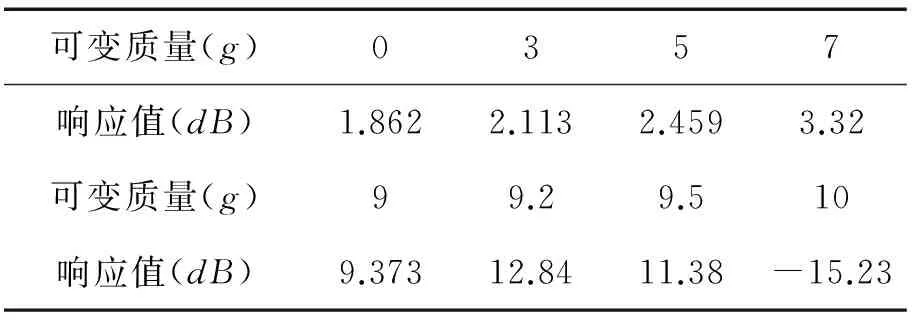
表2　不同质量的幅频响应值

从图3中还可以看出：虽然三组可变质量的最大值相同(均为10g)，但是主系统加速度响应的最大增加量不同，出现该现象的主要原因是质量变化速度不同造成的，质量变化越快，吸振器固有频率通过共振区的速度越快，则系统共振状态越难达到，因此主系统加速度响应的增加量则越小，反之则越大；主系统加速度响应随着质量变化时间的延长，系统到达稳态的时间也相应延长。因此，在质量增加控制过程中，控制质量变化越快越好，特别是当吸振器固有频率通过共振区时。

针对吸振器质量减小情况，采用与质量增加情况相同的仿真方法，设置激振频率为14.06Hz。吸振器可变质量由10g匀速减为0g，三组质量减小的具体变化过程如下式所示：

(6)

(7)

(8)

由式(6)～(8)可看出，三组变化过程的前10s吸振器可变质量均为10g，从第10s开始吸振器可变质量由10g逐渐减为0g，所用时间分别为6s、9.5s、11.5s。质量减小过程的主系统加速度时域响应如图4所示。

从图4中可看出，三组变化过程的主系统加速度响应均随着质量减小而减小，最终减为原来的16.86%，这与质量增加过程不同，主要是因为质量减小过程中，吸振器固有频率不会通过主系统共振区。利用仿真方法分别得出吸振器可变质量为10g、9.5g、9.2g、9g、7g、5g、3g、0g时，主系统幅频响应函数在14.06Hz处的响应值，如表3所示。从表3中可以看出：在14.06Hz处的主系统幅频响应值随着可变质量减少而不断减小。因此，主系统时域响应随着可变质量的减少而不断减小。

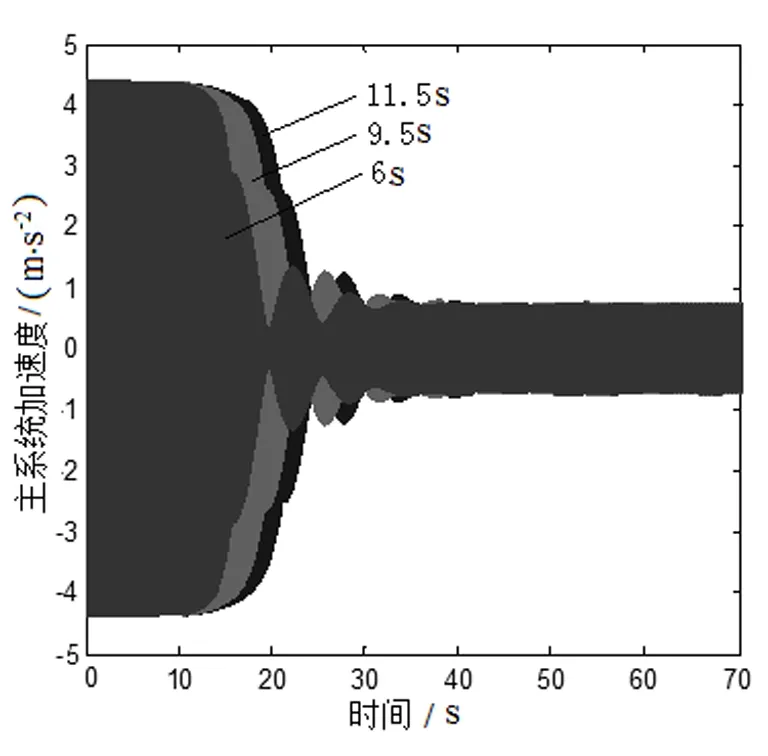
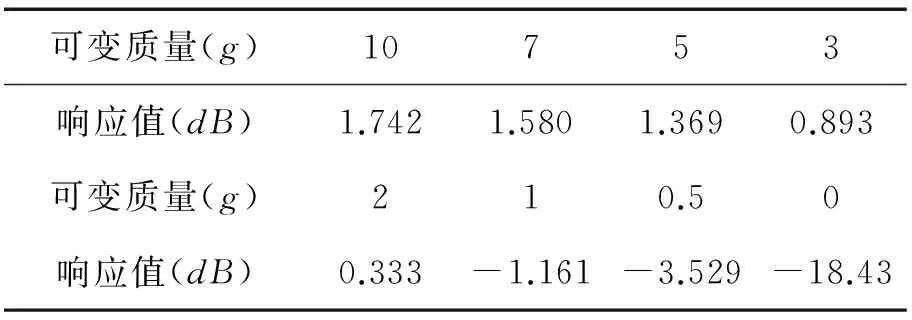
图4　主系统加速度时域响应

从图4中还可以看出：主系统到达稳态的时间随着可变质量变化时间的延长而延长，这与质量增加过程相同。因此在质量减小的控制过程中，同样是质量变化越快越好。

3结论

本文利用Matlab软件对变质量动力吸振器瞬态减振性能进行研究。通过仿真分析可得：吸振器质量增加和减少过程对瞬态减振性能的影响差别较大。吸振器质量增加过程，主系统加速度响应随着吸振器质量的增加先增加后减小，最终处于稳态；吸振器质量减少过程，主系统加速度响应随着质量的减少而减小，最终处于稳态。

对主系统加速度响应随吸振器质量变化的现象进行分析，并得出两种质量变化情况下主系统加速度响应差别较大的原因：吸振器质量增加过程，其固有频率将通过共振区，因此，主系统加速度响应随着质量增加先增加后减小；而质量减少过程，吸振器固有频率不通过共振区，其主系统加速度响应随着质量减少而不断减小。

分析了吸振器质量变化快慢对其瞬态减振性能的影响。吸振器质量变化越快，主系统加速度响应到达稳态的时间则越短，尤其在吸振器质量增加过程中，质量变化越快，主系统加速度响应的最大增加量也越小。

参考文献:

[1] 刘耀宗，郁殿龙，赵宏刚，等.被动式动力吸振技术研究进展[J].机械工程学报, 2007(3): 14-19.

[2]LariKela，PekkaVhoja.RecentStudiesofAdaptiveTunedVibrationAbsorbers/Neutralizers[J].AppliedMechanicsReviews,2009,62:060801-1-9.

[3]M.J.Brennan.Somerecentdevelopmentsinadaptivetunedvibrationabsorbers/neutralizers[J].ShockandVibration，2006,13:531-543.

[4] 郭年程，史文库，刘文军，等.动力吸振器在后桥振动控制中的应用[J].吉林大学学报:工学版,2012(6):3549-3554.

[5]MichaelJ.Brennan.Somerecentdevelopmentsinadaptivetunedvibrationabsorbers/neutralizers[J].ShockandVibration,2006，13:531-543.

[6]P.L.Walsh，J.S.Lamancusa.Avariablestiffnessvibrationabsorberforminimizationoftransientvibration[J].JournalofSoundandVibration,1992(02):195-211.

[7]H.X.Deng，X.L.Gong，H.Wang.Developmentofanadaptivetunedvibrationabsorberwithmagnetorheogicalelastomer[J].SmartMaterialsandStructures,2006(5):111-116.

[8]K.Williams，G.Chiu，R.Bernhard.Adaptive-passiveabsorbersusingshape-memoryalloys[J].JournalofSoundandVibration,2002(5):835-848.

[9] 徐振邦，龚兴龙，陈现敏.机械式频率可调动力吸振器及其减振特性[J].振动与冲击,2010(2):1-6.

[10]RustighiE，BrennanM.J，MaceB.R.，etal.Real-timecontrolofashapememoryalloyadaptivetunedvibrationabsorber[J].SmartMaterialsandStructure,2005,14:1184-1195.

[11]JLiu.Atunableelectromagneticvibrationabsorber:Characterizationandapplication[J].JournalofSoundandVibration,2006(02):708-724.

[12] 高强，房祥波，赵艳青，等.变质量动力吸振器及其减振性能[J].长安大学学报,2013(05):109-112.

(责任编辑:孙文彬)

Performance of Transient Vibration Reduction of Variable Mass Dynamic Vibration Absorber Mass Dynamic Vibration Absorber

ZHAO Yan-qing1，SONG Wei-zhi2，Sun Li1，BAO Hai-tao1

(1.Faculty of Traffic Engineering, Huaiyin Institute of Technology, Huai'an Jiangsu 223003, China；2.Department of Mechanical, Luoyang Institute of Science and Technology, Luoyang He'nan 471000, China)

Abstract:In order to study transient vibration attenuation effect of variable mass dynamic vibration absorber(VM DVA)and mass changing speed on transient vibration attenuation effect, a process of mass changing of absorber was studied via simulation on Matlab. The effect of mass changing speed on transient vibration attenuation was discussed and the reason of the difference between the two transient vibration attenuation effect was analyzed. The results showed that during the process of the mass increasing, the acceleration response of the primary system rose first and then fell down, eventually reached the steady state. While during the process of the mass decreasing, the acceleration of the primary system decreased all the time.

Key words:dynamic vibration absorber; variable mass; transient vibration analysis; Matlab simulation

收稿日期：2016-04-17

基金项目:国家自然科学基金项目(51505172)；江苏省前瞻性产学研合作基金项目(BY2015015-02)

作者简介：赵艳青(1985-)，男，山东菏泽人，硕士，主要从事非线性动力学数值计算和机械振动控制方面的研究。

中图分类号：O328

文献标识码：A

文章编号:1009-7961(2016)03-0057-04