基于压缩感知的三维人体点云的压缩及重建
刘 佳
(西安电子科技大学 电子工程学院,陕西 西安 710071)
基于压缩感知的三维人体点云的压缩及重建
刘佳
(西安电子科技大学 电子工程学院,陕西 西安 710071)
摘要经过激光扫描得到的三维人体点云数据量庞大,给模型的存储和传输带来困难,影响了其在体域网中的应用。针对这一问题,将压缩感知理论应用于人体点云模型的压缩与重建中。在压缩之前使用改进的三维栅格法做点云精简,针对人体点云的特点对数据进行分块稀疏变换,利用正交匹配追踪算法重建原始模型。最终实验重建误差约为 ,证实了该算法的有效性和可行性。
关键词压缩感知;点云精简;分块稀疏;匹配追踪
三维人体点云模型是通过激光扫描技术,对物理人体进行全方位扫描获取的。感兴趣的三维数据包括人体的身高、外形特征、体貌形态等元素。将采集到的数据经过三维建模软件可视化渲染后,方便后期参数调整和图像处理,这在体域网的实验研究中具有重要意义。但随着三维扫描设备的快速发展,扫描获得的数据量越来越大,占用的空间也越来越多,给存储和传输过程带来较大困难[1],本文将压缩感知理论应用在三维人体点云的压缩重建中,可有效解决上述问题。
1压缩感知理论
压缩感知理论指出[2-3]:具备稀疏特性的信号可被一个与变换基不相关的观测矩阵投影到低维空间中,然后通过求解一个欠定方程的优化问题就能从这些少量的投影中高概率地恢复原始信号。传统的信号获取过程,如图1所示,需要很高的采样频率,但采集到的大部分数据点在压缩的过程中被舍弃,这样无疑产生了浪费。压缩感知理论和传统的信息处理的最大区别在于其将采样和压缩过程同时进行,这样就能以远小于奈奎斯特采样定理所要求的采样频率采集并且较准确地重建初始信号。
压缩感知主要研究的数学问题如下[4]:N维的信号x∈RN×1映射到某一正交基{ψi}( 代表一个N维列向量),即
(1)

x=Ψθ
(2)
此处Ψ=[ψ1,ψ2,…,ψN]∈RN×N是正交基字典矩阵,θ=[θ1,θ2,…,θN]T。若θ中的非零系数的个数K≤N,则称θ是K稀疏的。采用一个与变换基矩阵Ψ不相关的观测矩阵Φ:M×N(M≪N)对信号进行采样压缩
y=Φx
(3)
这样就得到了M个线性测量结果,这一低维的测量结果已包含了重构原始信号的足够信息。压缩感知重构问题的实质是在已知测量信号y和观测矩阵Φ的条件下,怎样快速精确重构初始信号。

图1 传统的信号处理过程
2三维人体点云的精简和稀疏表示
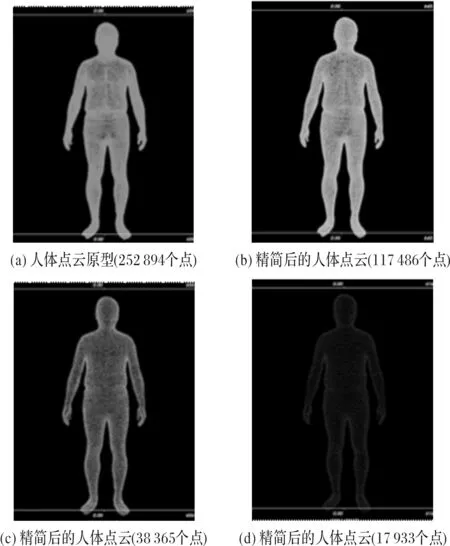
经过激光扫描生成的点云数据量庞大,这给后续数据采样压缩和恢复阶段的模型重构带来了不小的问题。通过分析点云中数据的密度等信息,可知点云中相邻点的间距只有毫米量级,这已经远超过了刻画人体细节所需要的密度,所以通过合适的算法来精简点云是可接受的[5]。
当前点云精简的基本方法主要有三维栅格法、三角网格法和曲率表示法等[6]。三维栅格法适用于外表光滑,曲率变化不明显的模型精简。三角网格法的思想是通过减少三角网格的数目来简化点云,但这种方法首先要对点云数据进行三角网格化处理。曲率表示法能将点云模型的细节精准地表示出来,缺点是计算时间复杂度较高。
本文采用的三维人体点云模型密度大,精确度高,且分布较为均匀,所以采用改进的三维栅格法对人体点云进行精简,即通过将点云数据分成很多微小的空间三维立方体的集合,然后在每个小立方体内用所有点的重心来近似表示其他邻域点,这种方法比用栅格中心来逼近的方法更准确,更不容易失真[7]。
点云数据具有分布于整个三维空间的性质,这对稀疏化的要求很高,构造字典矩阵要考虑点云的空间拓扑关系。通过分析点云中散乱点的分布,发现模型中任意两个相邻离散点的数值差别不大,具有较强的相似度,这说明点云的冗余度较高,可压缩空间较大。如果重新对点云中的数据进行组合排列,相关性就会变得更强。本文采用分块稀疏的方法,具体过程如下[8]:
步骤1点云降维。由于同一个点的3个坐标的相关性很小,而同一维度上的坐标值相关性较强,所以首先进行降维操作,将点云x方向,y方向和z方向的数据分开,分别组成x序列,y序列和z序列的数据集合;
步骤2点云分块。将降维后的数据按照某一坐标轴的大小进行排序,抽取点云中相同坐标分量的数据作为整体进行后续处理,若这些数据过长,截短为 个作为一个块单元进行处理;
步骤3点云变换。选取Haar小波矩阵作为字典矩阵,对分块后的点云数据做稀疏变换。
3点云数据的压缩和重建
要对初始信号进行精确重构,观测矩阵需要满足约束等距条件。研究人员已证实一些常用的矩阵直接符合约束等距条件的要求,本文使用高斯随机矩阵作为观测矩阵,使用如下函数生成
Φ=rand(M,N)
(4)
其中,M代表采样次数;M小于信号的维数,说明采样次数比传统采样次数少。最终生成的信号已经携带了原始信号足够的信息,也就完成了点云数据的采样压缩。
重建过程采用正交匹配追踪算法,初始化冗余向量r0=y,索引列表Λ0=φ,迭代次数t=1,算法步骤描述如下[9]
步骤1找到索引λ1,使得
(5)
步骤2 令Λt=Λt-1∪{λt},计算{Φλ:λ∈Λt}张成空间的正交投影Pt;
步骤3计算新的近似a和冗余r:at=Pty,rt=y-at;
步骤4t=t+1,若t (6) 正交匹配追踪算法[10]继承了匹配追踪类算法[11]的原子选择思想,有效减少了迭代次数,降低了时间复杂度。按照上述算法依次恢复数据块中的每一维数据,最后使用逆排序恢复初始的人体点云。 4实验与结果分析 4.1点云精简效果仿真 实验使用的三维人体点云由117 486个点构成,从三维人体点云原图和精简后的图像可知,此种精简算法处理后的模型不会影响人的视觉感受,人体外形轮廓基本与原型一致,没有造成特征丢失和模糊。 图2 点云精简效果对比 通过改变栅格的粒度来对比精简效果,得到表1所示,可看出随着栅格长度的增大,简化程度逐渐变大,点云点数从117 486降低到17 933,保存点云数据的文件大小从3.5 MB降低到544 kB,当然随着简化程度的逐步增大,程序执行的时间也越来越长。从表中可知三维栅格精简算法能够有效地减少点云中的数据量,达到简化模型的作用。 表1 不同栅格长度下点云精简效果对比 4.2点云重建效果仿真 本实验综合评估各项因素,对精简后的点云进行压缩,根据分块稀疏变换后的稀疏度,将压缩比设定为0.6,重建效果对比如图3所示,可看出重建的三维人体点云模型基本轮廓与原始模型保持一致,并没有出现外形上的变化和失真,也能较好地保留点云细节之处的形态。为了定量地对重建效果进行评估,计算重建点与对应的原始点的欧式距离,然后将距离累加求均值,评估重建效果的公式为 (7) 其中,Xi表示原始人体点云中的数据点;Ri表示重建的点云中相同位置处对应的数据点;N代表点云的数目,经过计算求得误差接近2.17×10-5,结果令人满意。但从图3中也可看出,重建的三维人体模型在一些曲面交汇处出现粘连现象,这是由于精简后的点云密度降低,点间距变大,造成在一些交界轮廓处构建的三角形顶点不在同一曲面上。可通过精简时降低栅格的大小和使用其他改进的重建算法来改善这一问题,这也是进一步的研究方向。 图3 人体点云重建效果对比 5结束语 压缩感知理论的提出给信号采集处理领域带来了新的发展方向,本文将此理论应用于三维人体点云模型的压缩和重建中,可有效降低模型数据的传输复杂度,减小计算机存储的压力,这将大幅拓展三维人体点云模型在体域网中的应用范围。 参考文献 [1]王鹏杰,潘志庚,刘勇奎.基于点的三维模型压缩技术研究进展[J].计算机辅助设计与图形学学报,2009,21(10):1359-1367. [2]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):4036-4048. [3]Candès E,Romberg J,Tao T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on an Information Theory,2006,52(2):489-509. [5]焦李成,杨淑媛,刘芳,等.压缩感知回顾与展望[J].电子学报,2011,39(7):1651-1658. [6]李鹏飞,侯毅星,景军锋.三维人体的点云获取与点云重建[J].西安工程大学学报,2014,28(1):72-76. [7]朱煜.散乱点云数据简化及三角网格重构的研究[D].西安:西北大学,2012. [8]朱德海.点云库PCL学习教程[M].北京:北京航空航天大学出版社,2012. [9]张习民,余小清,万旺根,等.压缩感知点云数据压缩[J].应用科学学报,2014,32(5):458-462. [10]方红,杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421. [11]Tropp J,Gilbert A.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666. [12]Mallat S,Zhang Z.Matching pursuit with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415. Compression and Recovery of 3D Body Point Clouds Based on Compressed Sensing LIUJia (SchoolofElectronicEngineering,XidianUniversity,Xi’an710071,China) AbstractWith higher precision of the laser 3D scanning, the growing point cloud model data lead to the difficulty of data storage and transmission, thus limiting its application in the body network. In order to solve this problem, the compressed sensing technique is applied to the compression and reconstruction of human body point clouds model to perform data simplification processing by the improved three-dimensional grid method before compression. In light of the characteristics of human point cloud data, the block sparse transformation and orthogonal matching pursuit algorithm is applied to reconstruct the original model. The final experimental error is only , which confirms the validity and feasibility of the algorithm. Keywordscompressed sensing; data simplification; block sparse; matching pursuit 收稿日期:2015- 11- 16 作者简介:刘佳(1990-),男,硕士研究生。研究方向:物联网技术与Web开发。 doi:10.16180/j.cnki.issn1007-7820.2016.07.021 中图分类号TP317.4 文献标识码A 文章编号1007-7820(2016)07-072-03