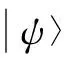基于优超理论的纠缠纯态转化*

孙照龙， 胡占宁， 孔令浩， 靳瑶瑶

(天津工业大学 理学院，天津 300387)



基于优超理论的纠缠纯态转化*

孙照龙， 胡占宁， 孔令浩， 靳瑶瑶

(天津工业大学 理学院，天津 300387)

摘要：利用优超理论实现了高维量子系统中局域纠缠纯态的确定转化；在一个4⊗4维量子系统的低维子系统中两次利用优超理论，并通过正定算符值测量(Positive Operator Valued Measure，POVM)、算子测量、局域操作和经典通信(Local Operations and Classical Communication，LOCC)，最终实现了4⊗4维量子系统中的纯态以100%的概率完成转化。通过计算和理论推导说明这种基于优超理论的纠缠纯态转化会降低量子子系统Von Neumann熵。

关键词：纯态转化；优超理论；POVM；Von Neumann熵

量子信息是一门基于量子力学和信息学的交叉学科。近年来，随着现代通信技术的发展，量子信息无论是在理论还是在实验方面都取得了令人瞩目的成就。其中，量子纠缠更是扮演着重要的角色，它作为量子信息的基本资源之一被广泛应用于量子隐形传态[1]、量子计算[2]和量子密码学[3]等方面。量子纠缠纯态转化问题是量子信息学中的基础问题，对它的研究将会加深对微观世界的认识。

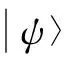
1优超理论与施密特分解

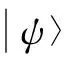
(1)

(2)

(3)

对于∀l(1≤l≤n)都满足，当l=n时，式(3)取得等号。

2 4⊗4维纠缠纯态的确定转化

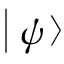
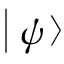
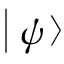
(4)

(5)

式(4)(5)中取

(6)

(7)

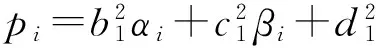
1) 当c1≥c2时，所选取的一组具体的POVM算子为

将这3个测量算子代入式(7)，可以得到

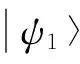
2) 当c1≤c2时，所选取的另一组POVM算子为

将这3个测量算子代入式(7)得到

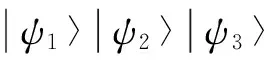
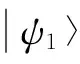
(8)

式(8)中取

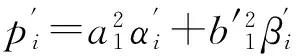
针对第2步转化，选取的一组POVM算子：

3优超过程中量子子系统Von Neumann熵的变化

Von Neumann熵是量子通讯领域[8]中最基本也是最重要的概念，其地位与经典信息理论中的Shannon熵的地位相当。基于密度矩阵，以量子态为研究对象，由Von Neumann熵的定义可以得出优超转化中某一过程的约化熵为

S(b,c)=-b2log2(b2)-c2log2(c2)-

(1-b2-c2)log2(1-b2-c2)

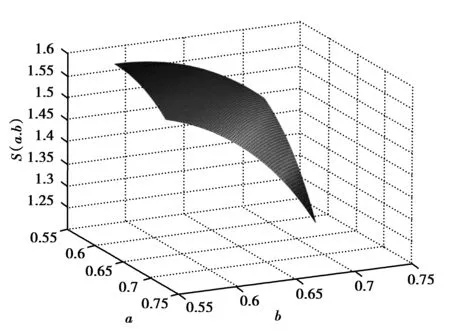
图1　量子熵S(a,b)的变化趋势Fig.1　Changing trend of quantum entropy S(a,b)

图2　量子熵S(b)的变化趋势Fig.2　Changing trend of quantum entropy S(b)

下面分析n⊗n维量子系统进行优超操作后Von Neumann熵的变化情况。对定义在集E⊆Rn上的实值函数F，若F对E中满足x

这说明了基于优超理论的n⊗n维纠缠纯态的转化会降低量子子体系Von Neumann熵。

4总结

给出了利用优超理论所构建的操作方案实现4⊗4维纠缠纯态转化的一般过程，该过程主要通过构造几种不同的POVM算子方案来实现纠缠纯态转化，并给出POVM算子作用后生成的量子态及其各自的生成概率，最后利用局域操作将所生成的量子态转化为所需要量子态。同时，通过计算说明这种基于优超理论的转化成功的概率为1，从而克服先前的纯态转化只能在低维系统中进行的缺陷。最后，通过Schur凹函数的特性说明了这种基于优超理论的纠缠纯态转化会引起子系统Von Neumann熵的降低。这样就把优超理论在纠缠纯态转化中的应用做了进一步的完善和拓展，为这种理论的进一步推广和实验上的实现奠定了基础。

参考文献(References)：

[1] BENNETT C H,BRASSARD G.Teleporting an Unknown Quantum State Via Dual Classical and Einstein-Podolsky-Rosen Channels[J].Phys Rev Lett,1993(13):1895-1901

[2] NIELSEN M A.Quantum Computation and Quantum Infor-mation[M].Cambridge:Cambridge University Press,2000

[3] ARTUR K,EKER.Quantum Cryptography Based on Bell’s Theorem[J].Phys Rev Lett,1991,67(6):661-663

[4] JONATHAN D, MARTIN B,PLENIO.Entanglement-Assisted Local Manipulation of Pure Quantum States[J].Phys Rev Lett,1999,75(17):3566-3570

[5] TORUN G,YILDIZ A.Deterministic Transformations of Bipartite Pure States[J].Phys Lett A,2002(3):113-118

[6] MARSHALL A W,OLKIN I.Inequalities:Theory of Majori-zation and its Applications[M].New York:Springer,2010

[7] 梁林梅.量子纠缠和纠缠转换的研究[D].长沙:国防科学技术大学,2002

LIANG L M.Study on Quantum Entanglement and Entang-lement Transformation[J].Changsha:National University of Defense Technology,2002

[8] 胡冬梅,冉扬强,黄晓春.原子与双光场耦合系统量子信息保真度研究[J].重庆工商大学学报(自然科学版),2007,24(2):143-147

HU D M,RAN Y Q,HUANG X CH.Research into Fidelity of Quantum Information in Atom’s Coupling to two Optical Fields System[J].Journal of Chongqing Technology and Business University (Natural Science Edition),2007,24(2):143-147

[9] 杨定华.抽象控制不等式的理论基础[J].中国科学,2009,39(7):873-891

YANG D H.Theoretical Basis of the Abstract Control Inequality[J].Science in China,2009,39(7):873-891

责任编辑：李翠薇

doi:10.16055/j.issn.1672-058X.2016.0004.009

收稿日期：2015-11-23；修回日期：2016-01-12.

*基金项目：国家自然科学理论物理专项基金(11447153).

作者简介：孙照龙(1990-)，男，安徽合肥人，硕士研究生，从事量子信息学研究.

中图分类号：O431

文献标志码：A

文章编号：1672-058X(2016)04-0053-05

Entanglement Transformation of Pure States Via Theory of Majorization

SUN Zhao-long, HU Zhan-ning, KONG Ling-hao, JIN Yao-yao

(School of Science, Tianjin Polytechnic University, Tianjin 300387, China)

Abstract：This paper uses the Theory of Majorization to accomplish deterministic transformations of the entangled bipartite pure states in the high dimensional quantum systems. There is a detail process that a 4⊗4 dimension quantum system completes the deterministic transformations with a one hundred percent probability by the Theory of Majorization, local operation and classical communication (LOCC) and positive operator valued measure (POVM). By the calculation and theoretical derivation, this entangled pure state deterministic transformations based on the Theory of Majorization can decrease the Von Neumann entropy of quantum subsystem.

Key words：pure state transformation; Theory of Majorization; POVM; Von Neumann entropy