单动叶安装角异常时轴流风机压力脉动特性的数值分析

叶学民，　丁学亮，　李春曦

(华北电力大学 电站设备状态监测与控制教育部重点实验室， 河北保定 071003)



单动叶安装角异常时轴流风机压力脉动特性的数值分析

叶学民，丁学亮，李春曦

(华北电力大学 电站设备状态监测与控制教育部重点实验室， 河北保定 071003)

摘要：以OB-84型动叶可调轴流风机为对象，对单动叶安装角在不同偏离度下的风机内部流场特征和性能进行了非定常计算，得到了安装角异常下压力脉动的时域和时频特性、静压时均值及等效应力分布.结果表明：动叶安装角异常时，各监测点的压力信号及压力脉动能量均出现异常特征，尤其是叶轮出口处的变化最为突出；动叶异常偏离对时域和时频特性的影响程度随偏离度的增大而提高，并导致压力脉动强度增大；各监测点的近似熵在大偏离度下变化显著，对动叶异常偏离具有良好的表征能力；静压时均值的分布和数值随偏离度改变均有较大变化，而叶片等效应力仅在数值上有明显改变.

关键词：动叶可调轴流风机； 偏离度； 安装角异常； 压力脉动

动叶可调轴流风机因其结构简单紧凑、运行范围广及变工况效率高等特点而广泛用于航空航天、能源、动力和交通等领域.但其内部结构复杂，变工况运行时，常因执行机构故障引发动叶安装角异常偏离的现象，造成风机不规则振动，从而影响风机的安全运行[1].研究表明，该不规则振动主要是因动叶发生异常偏离后、内部非定常流场及压力脉动的变化所致[2].因此，深入研究动叶发生异常偏离时风机内部的压力脉动特性及其内部流场分布至关重要.

目前，对于轴流风机的研究多集中在内部流场特性与结构优化[3-5]、失速与喘振[6-8]、叶顶间隙对风机性能的影响[9-11]及噪声[12-14]等方面，并取得了丰厚的研究成果.关于通风机非定常流场和压力脉动方面，陈庆光等[15]利用大涡模拟方法通过对旋轴流风机的非定常计算，分析了各监测点下的压力脉动频率、强度及成因.Ballesteros-Tajadura等[16]模拟了离心风机叶轮及机壳处的压力脉动，得到了压力时域和频谱分布特性，其计算结果与实验值吻合良好，但其研究仅分析了压力脉动特性，未对内部流场分布进行研究.Jiro等[17]通过修正离心力、重力和其他主要误差的影响，准确测得某轴流风机的瞬时压力特征，但其风机结构较为简单，所得结论不具有普遍性.

对于动叶安装角异常时的轴流风机，叶学民等[18-19]通过对两级动叶可调轴流风机的数值研究，得到了第一级动叶发生异常偏离及两级动叶均异常偏离对风机性能和内部流场的影响，但其分析基于定常计算结果.在非定常计算方面，Posson等[20]利用宽频噪声模型分析了动叶偏移时的声功率分布特征.李春曦等[21]通过非定常计算得到轴流风机内声压信号的时域和频域特性，分析了轴流风机内气动噪声的分布，但对于风机异常偏离时压力的非定常特性和局部压力脉动特性尚未展开研究.

鉴于目前动叶可调轴流风机的非稳态流动研究尚不完善，尤其是对动叶异常偏离时风机内部的压力脉动特性尚未完全认识.为此，笔者采用Fluent软件对OB-84型动叶可调轴流风机开展非定常计算，进而分析动叶异常偏离对压力时域和时频特性、静压时均值及等效应力分布的影响，为风机安全稳定运行及优化设计提供参考依据.

1计算模型

以OB-84型单动叶可调轴流风机为研究对象，其结构包括集流区、动叶区、导叶区和扩压区.该风机有14片动叶、15片导叶，叶轮直径为1 500 mm，叶顶间隙为4.5 mm，转速为1 200 r/min，由此可得叶片通过频率为280 Hz，风机结构和参数详见文献[22].实际运行中，动叶安装角正向偏离现象较常见，因此笔者对单动叶安装角偏离度Δβ=0°～50°进行研究，Δβ=0°表示动叶安装角处于正常状态(此时动叶安装角为32°)，不同偏离度表示该动叶沿翼型轴线逆时针旋转相应的度数，如图1所示.

图1　动叶安装角偏离度

基于动叶可调轴流风机的结构特点，采取分区和局部加密划分方法，在动叶区因流动梯度及曲率变化大，故采用加密网格;而集流区、导叶区和扩压区采用稀疏网格，以减少计算量.模拟中，为验证网格无关性，选取163万、197万、235万和260万4组网格数进行计算.模拟显示，计算精度和计算时间均随网格数的增加而提高，当网格数为235万时，可同时满足计算时间和计算精度的要求，故选取该网格数对风机性能进行模拟，此时动叶区和导叶区的网格数分别为135万和21万.

定常计算采用Realizablek-ε湍流模型，该模型因引入旋转和曲率相关项，而广泛用于旋转均匀剪切流、射流、混合流的自由流动和带有分离的流动[18-19,21].同时，选用多参考系模型解决叶轮中叶片与机壳间动静干涉面数据传递的问题.计算中，风机入口边界条件为入口速度，出口边界条件为自由流出，不同区域的交界面上采用interface实现各区域交界面上流体参数的交换.模拟中，当各参数残差均小于10-4，且进、出口截面的总压均不随时间改变时，则视计算已收敛.

将上述计算所得流场作为非定常计算的初场，由于滑移网格计算时只需要计算交界面两侧的通量且使其相等，即可实现动静干涉面间的信息传递，故非定常计算选用滑移网格模型进行动静干涉面的数据传递.因风机内的气流在动叶区获得机械能，在导叶区改变其流动方向，故动叶区和导叶区气流的压力脉动比集流区和扩压区气流的压力脉动更为显著.为此，笔者主要研究动叶区和导叶区压力信号的时域和时频特性.经验证同一个径向截面监测点的压力特性相似，为此每个截面只取一个具代表性的监测点进行分析，将压力信号监测点分别布置在动叶入口(P1点)、叶顶间隙(P2点)、动叶出口(P3点)和导叶出口(P4点)，如图2所示.

图2　监测点位置分布

2模拟结果与分析

2.1时域分析

在计算动叶异常情形前，首先对正常情形下的风机进行数值模拟，以验证数值模拟的准确性.结果表明，在模拟流量范围内，所得全压与实验数据相比，平均偏差为1.7%，保证了数值模拟的可靠性.

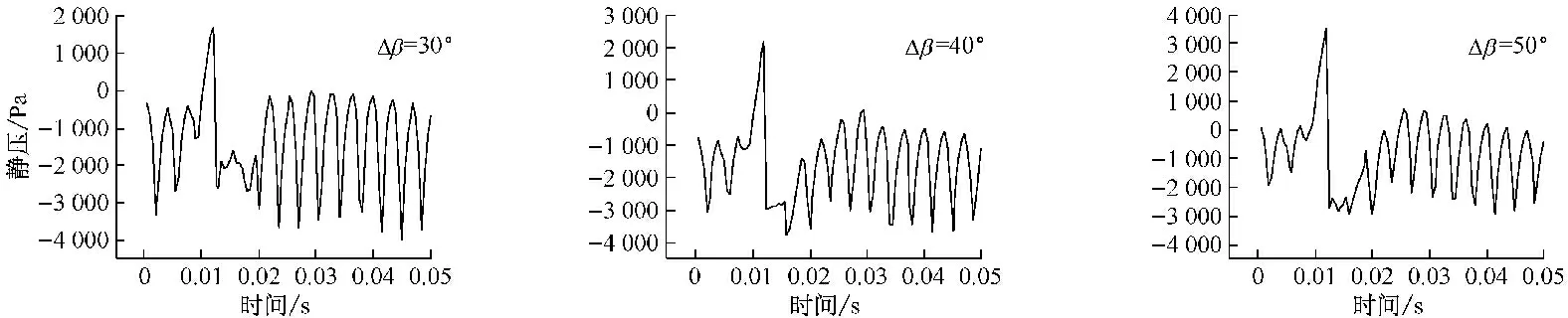
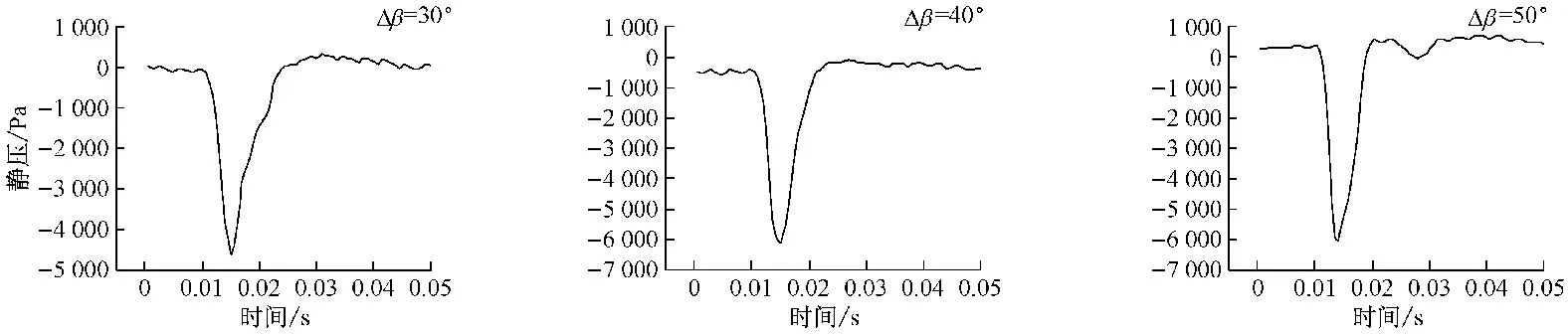
为研究不同偏离度下，压力信号随时间的变化特征，图3给出了叶轮旋转一个周期内的静压时域分布.从图3可以看出，正常情形下，不同监测点的压力信号随时间变化均呈周期或类周期性波动.这是由于叶轮旋转过程中动叶周期性击打周围空气所致，每个周期具有14个明显峰值点，其个数与动叶数一致.另外，沿气流流动方向，P1～P4点静压时均值逐渐增大，脉动幅度却呈减小趋势，这是因为沿P1～P4点所在截面，气体不断获得机械能，进而静压逐渐提高，由此使得静压时均值增大；同时，气流逐渐远离提供能量的动叶，因而其脉动幅度逐渐减小.

从图3还可以看出，异常情形下，动叶入口处的P1点峰值点个数未改变，在0.01～0.02 s间出现异常波动.在此区域内，峰值处的静压值显著增大、而谷值处的静压值则显著降低，且Δβ越大，峰谷间的脉动幅度更加突出，当Δβ=50°时，其脉动幅度约为正常情形下的11倍，而其他时间区的压力脉动变化不明显.叶顶间隙处的P2点在0.01 s附近的静压峰值异常增大，随Δβ的增加异常波动区有所变化，其中，Δβ=10°时仅在0.01 s附近出现一异常峰值点，而Δβ=50°时其影响范围则扩大到0.015 s.动叶异常偏离对P3和P4点处静压值的影响整体呈现相似趋势：正常情形下，静压值均为正值，而动叶异常偏离后，尤其是Δβ较大时，静压值为负值且脉动幅度较大，波动时间范围也扩至0.01～0.03 s，并呈“V”形分布.其原因是气流通过异常动叶时，流动角改变造成冲角增大，使得动叶对通过该通道气流的击打强度增大，进而造成峰谷间的压力脉动幅度随Δβ增大而增大，并对后续时间的压力脉动产生明显的影响.可见，动叶异常偏离后各监测点的时域特性明显不同，但压力异常波动范围相似，且其影响程度随Δβ的增大而增强.

2.2压力脉动强度

为进一步研究不同监测点处的非定常流动特征，将瞬时压力转化成无量纲压力系数Cp(t)=p(t)/0.5ρu22，其中ρ为流体密度，p(t)为某时刻t下的静压值，u2为叶轮外圆周速度.一个周期内压力系数的平均值和压力脉动强度[23]由式(1)和式(2)确定：

(1)

(2)

其中，N为一个周期内的数据长度.

图4给出了各监测点在不同偏离度下的压力脉动强度.从图4可以看出，正常情形下，P2点的压力脉动强度远高于其他监测点.动叶异常偏离后，P2点的压力脉动强度随Δβ的变化并不明显，而P1、P3和P4点的压力脉动强度则呈升高趋势.这是因为在叶顶间隙处，异常动叶对静压值的影响有限；而在动叶入口、动叶出口和导叶出口处，随Δβ的增大，异常动叶造成当地静压值发生显著变化，导致其压力脉动强度提高，以及由此对上下游流动的干涉作用逐渐增强.其中，P3点的增幅最为显著，而P1和P4点的压力脉动强度随Δβ的增幅相差不大.可见，动叶异常偏离对叶顶间隙处压力脉动强度的影响较小，而对动叶出口处压力脉动强度的影响最大.

2.3时频分析

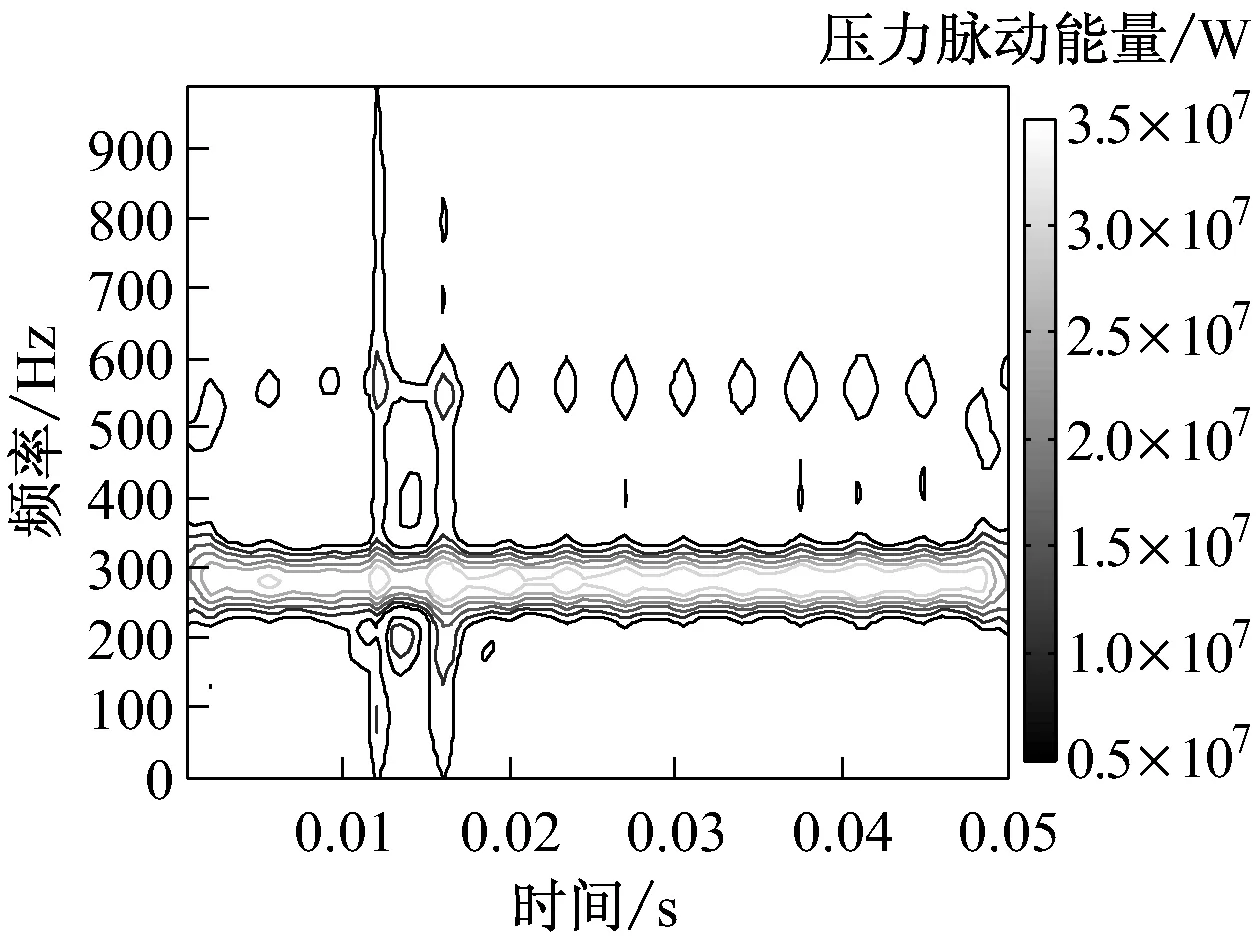
时频分析能同时描述信号在不同时间和频率的能量密度和强度.选用Choi-Williams分布描述信号的时频能量分布，该分布可消除典型Wigner-Vill分布中的交叉干扰项，但计算量无明显变化[24].

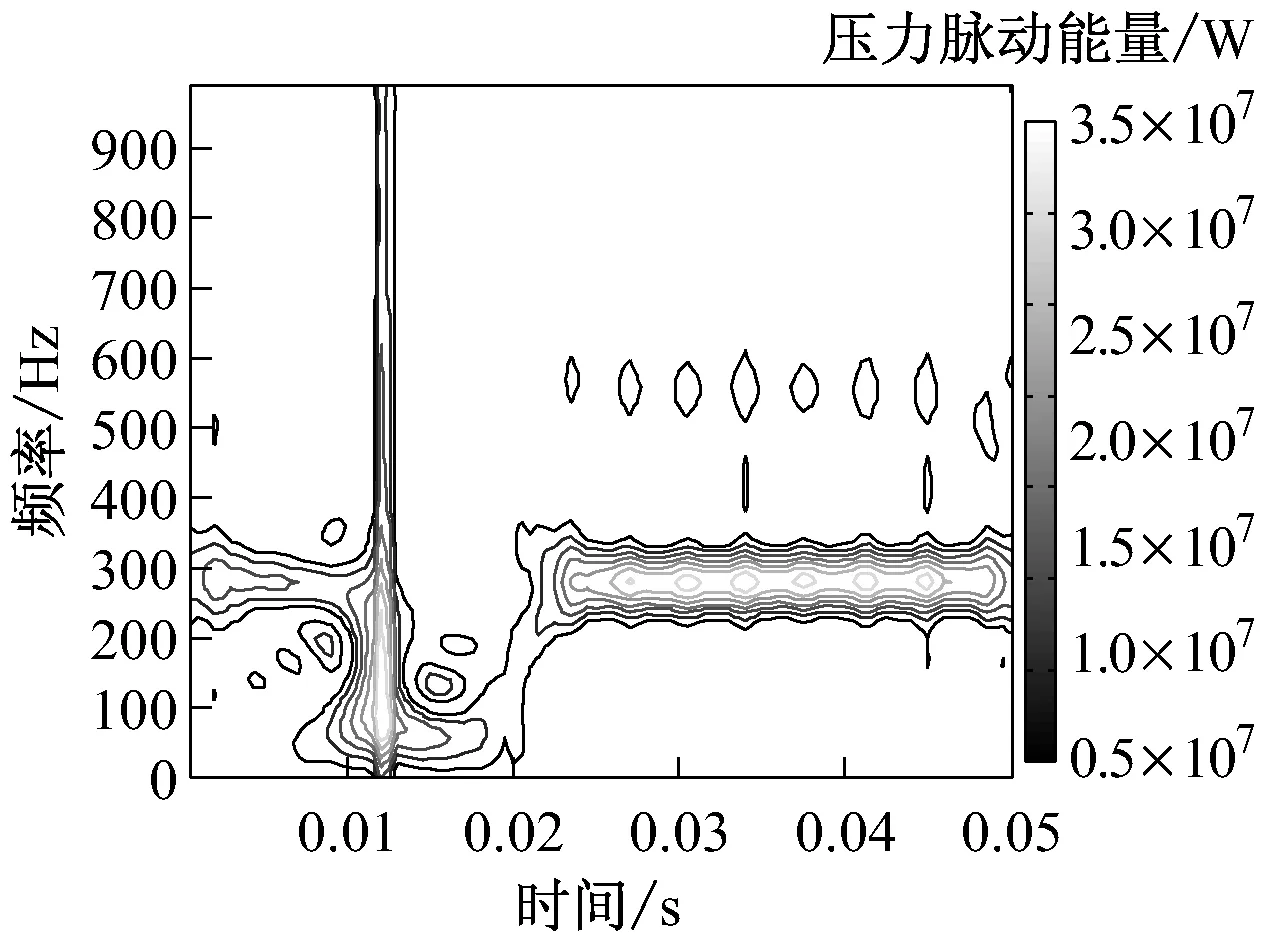
图5为不同偏离度下P2点的时频分布.由图5可知，正常情形下，压力脉动信号在280 Hz附近出现最高点，这与叶片通过频率相一致，同时压力脉动能量主要集中于200～400 Hz频率段，在500～600 Hz(包括2倍叶片通过频率)间存在较低的压力脉动能量.动叶异常偏离后，各偏离度对时频分布的影

(a) P1

(b) P2

(c) P3

(d)P4

图3时域特性

Fig.3Characteristics of static pressure in the time domain

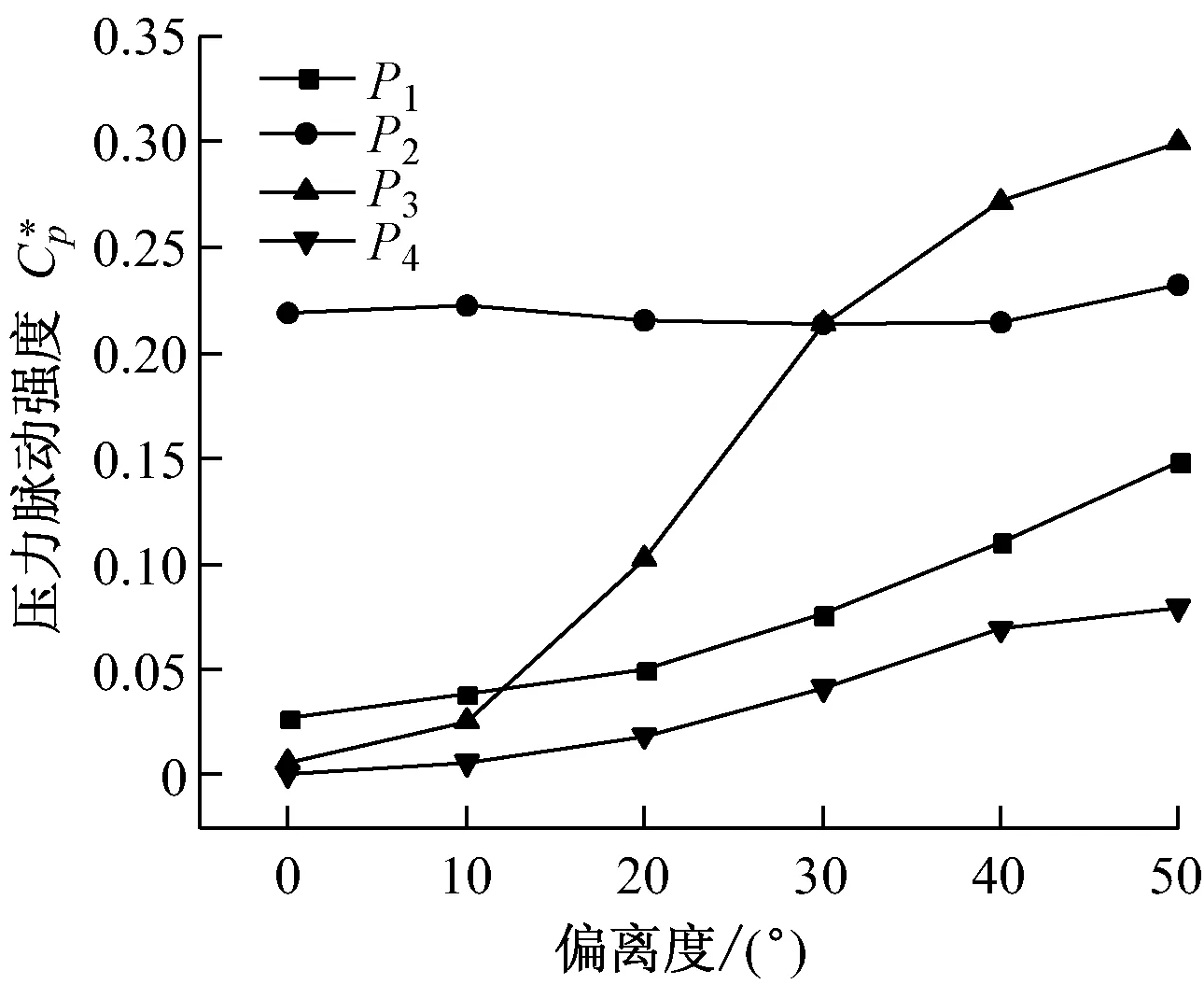
图4　不同偏离度下的压力脉动强度

响有所不同.Δβ=10°时，在0.01～0.02 s间的压力脉动能量出现异常分布，这与图3(b)中的异常波动时间区间相符，除在1倍及2倍叶片通过频率附近，其他频率段也出现压力脉动能量值，但这些能量处于较低水平；Δβ=20°时，t=0.013～0.025 s压力脉动能量显著减小，而小于此区间的能量降幅相对较小，其他区间的能量分布变化不明显；Δβ=30°时，在0.012 s处产生最大压力脉动能量，同时在整个频率区间内均存在压力脉动能量，t<0.012 s时的压力脉动能量减小；Δβ=40°时，t=0.01～0.02 s内的压力脉动能量分布变化不大，仍为能量集中区，而其他波动时间区间的能量显著减小；Δβ=50°时，与Δβ=40°相比，压力脉动能量仅在数值上存在差异，其分布规律相似.总体上，压力脉动能量最大值随Δβ的增大呈增大趋势，即偏离度越大，动叶异常偏离对时频分布的影响越明显.

(a) Δβ=0°

(b) Δβ=10°

(c) Δβ=20°

(d) Δβ=30°

(e) Δβ=40°

(f) Δβ=50°

2.4近似熵

近似熵算法最早由Pincus提出，其值能够表征信号的复杂度，因此越复杂的信号近似熵越大.近似熵能根据较短数据得出比较稳健的估计值，同时具有良好的抗噪和抗干扰能力，其表达式为：

(3)

式中：r为相似容限；m为模式嵌入维数；Φm(r)为压力信号的对数平均值[25].

选取m=2，r=0.2S，S为原始数据的标准差[25].

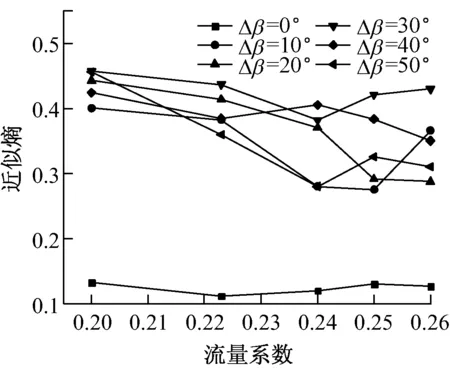
图6为各监测点在不同流量系数下的近似熵分布.由图6可知，各监测点的近似熵呈现不同的特征.动叶入口处P1点的近似熵在正常情形下处于较低水平且随流量系数的增大变化不明显，而动叶异常偏离后，近似熵均明显增大，同时随Δβ的增大，近似熵的平均水平呈先增后减的趋势.对于叶顶间隙处的P2点，其异常情形下的近似熵同样显著高于正常情形，但其近似熵总体随Δβ的增大而增大.对于动叶出口处的P3点，其正常情形下的近似熵与Δβ=10°时相差不大，当Δβ进一步增大后，近似熵则显著减小，其中，Δβ>20°时近似熵的降幅减小.对于导叶出口处的P4点，动叶异常偏离后的平均近似熵均小于正常情形，且随Δβ的增大总体呈减小趋势.

(a) P1

(b) P2

(c) P3

(d) P4

上述分析表明，P1、P2点处在正常情形下的近似熵小于异常情形，而P3、P4点则相反，这是由于近似熵大小与信号复杂度有关.由图3可知，P1、P2点在正常情形下的压力信号呈周期性波动，其峰值、谷值随时间变化不明显，而动叶异常偏离后的压力信号出现了异常波动，使压力信号复杂度增加，因此近似熵变大；P3、P4点在正常情形下的峰值、谷值随时间变化显著，压力信号复杂度较大，动叶异常偏离后的压力信号呈较规律的“V”形分布，故动叶异常偏离后近似熵呈减小趋势.可见，近似熵对动叶异常偏离有很好的辨识能力.

2.5静压时均值分布

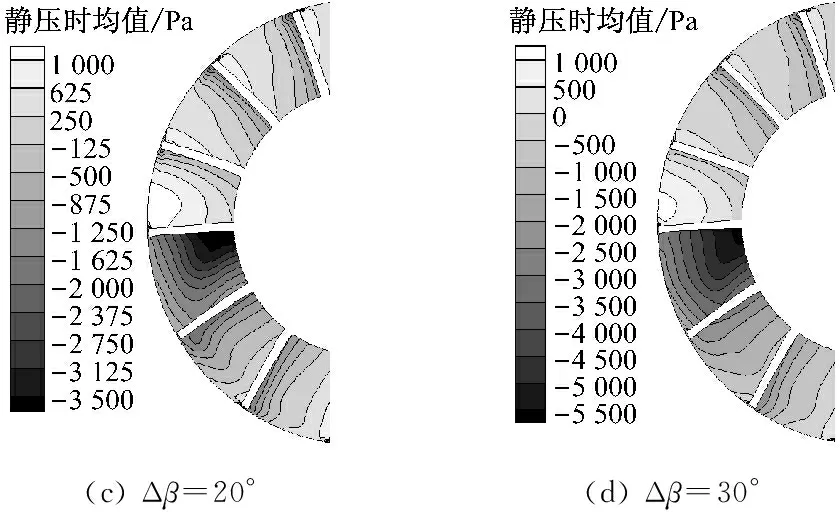
静压时均值可反映静压随时间的变化率及流道内流动的非定常特征.图7给出了叶轮中间截面上的静压时均值分布，叶轮旋转方向如图所示.由图7可知，正常情形下，流道内的静压时均值从压力面到吸力面呈下降趋势，在靠近叶顶处出现最小值.当动叶异常偏离后(见图7(b))，异常动叶压力面侧的高压区范围扩大，吸力面则在靠近轮毂处产生低压区.这是由于动叶异常偏离导致边界层脱落的涡流与流道内的主流相互作用增强，使得叶片压力面和吸力面侧流道内的静压时均值分布发生改变，而其他流道静压时均值变化不明显.

当Δβ进一步增大(见图7(c)～ 图7(f))，异常动叶吸力面侧的低压区范围扩大，且低压区静压时均值也逐渐降低，在逆旋转方向上与异常动叶相邻叶片的流道也受到影响，尤其是Δβ=50°时异常动叶吸力面侧的整个流道处于负压水平，逆旋转方向上与异常动叶相邻叶片吸力面侧的低压值从叶片中上部移至中下部.可见，随Δβ的增大，动叶异常偏离对静压时均值的影响程度提高.

(a)Δβ=0°(b)Δβ=10°

(c)Δβ=20°(d)Δβ=30°

(e)Δβ=40°(f)Δβ=50°

图7叶轮中间截面上的静压时均值分布

Fig.7Contour of time-averaged static pressure on the middle surface

2.6等效应力分布

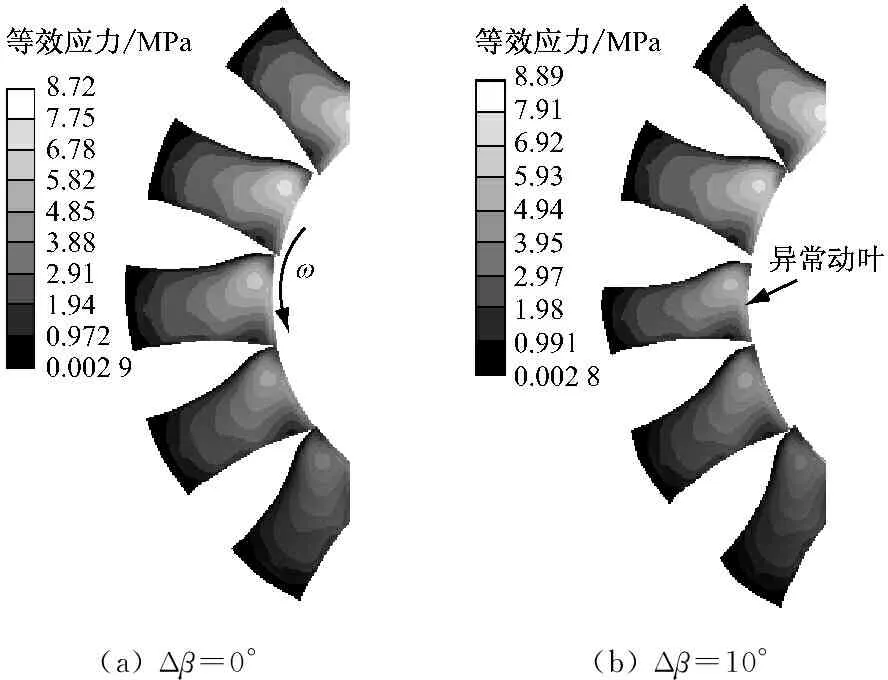
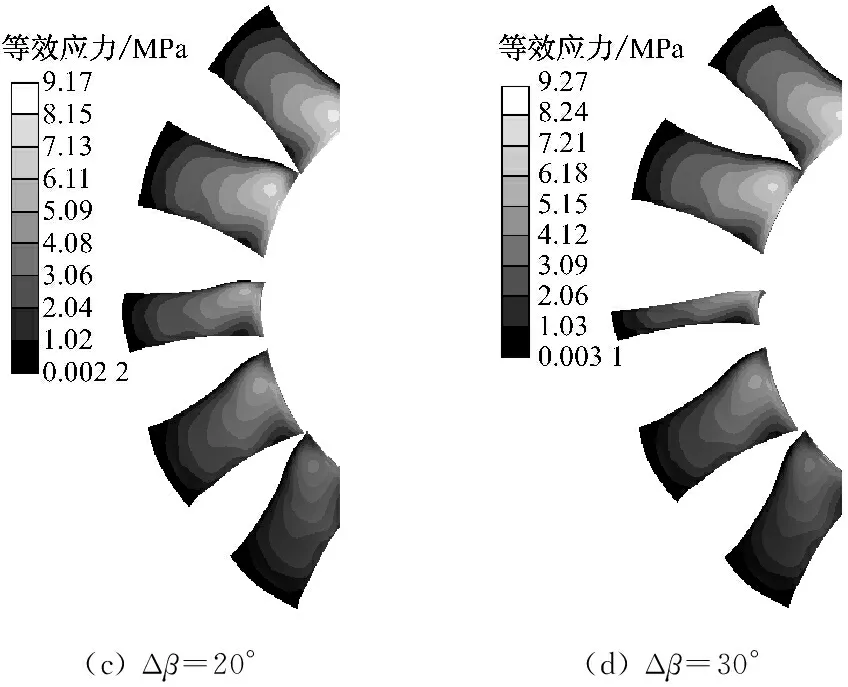
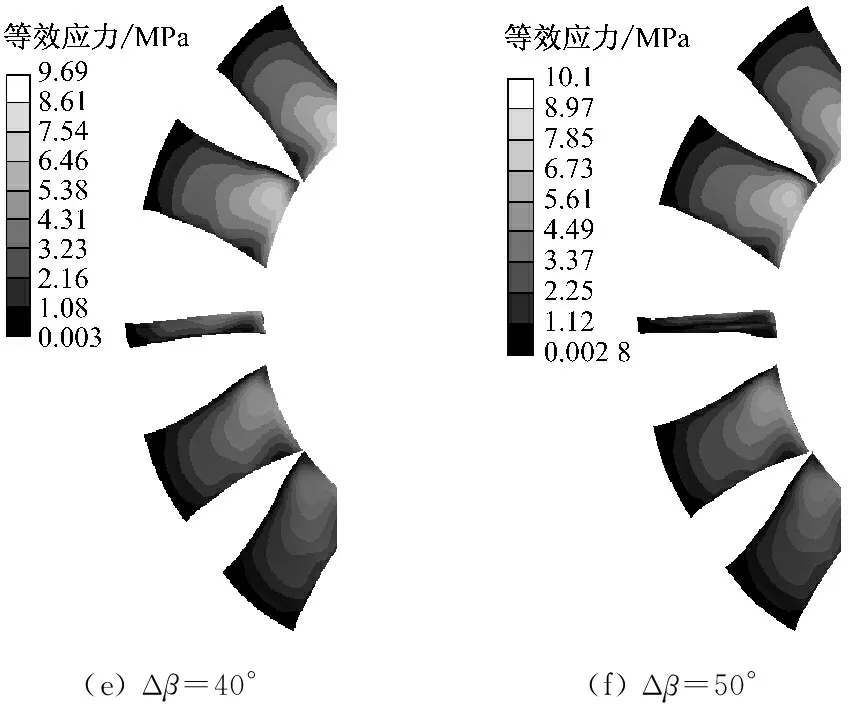
以上分析表明，动叶发生异常偏离后改变了流道内的压力分布，从而导致叶片表面载荷也发生变化，因此，有必要分析动叶异常偏离对叶片等效应力的影响.图8给出了不同偏离度下的叶片等效应力分布.由图8(a)可知，正常情形下，最大等效应力值集中于吸力面叶根靠近前缘处，且等效应力沿叶高方向逐渐减小.这是由于叶根固定在轮毂上且截面积最大，叶轮转动过程中承受整个叶片的离心力，因此应力集中于叶片根部.Δβ=10°～30°时，如图8(b)～图8(d)所示，随Δβ的增大，叶片等效应力分布变化不明显，但最大等效应力值呈增大趋势.Δβ=40°和50°时，如图8(e)和图8(f)所示，最大等效应力值进一步增大，且集中于异常叶片吸力面侧，而其他叶片高等效应力区范围也有所扩大.

在强度计算中，塑性材料的许用应力[σ]=σs/ns，其中σs为材料的屈服极限，ns为塑性材料的安全系数.对于弹性结构加载静力载荷的情况下，ns取值范围为1.5～2.所研究风机叶片的材料为铸铝ZL101，其屈服强度σs为180 MPa，ns取2，可得出叶轮的许用应力值为90 MPa.图8中最大等效应力值为10.1 MPa，小于许用应力值.因此，轴流风机动叶异常偏离后仍满足强度要求.

3结论

(1) 动叶异常偏离后各监测点压力信号的周期性或类周期性波动被破坏，均出现不同程度异常波动，且偏离度越大其影响程度越明显；动叶出口处的压力脉动呈“V”形分布，其影响时间也明显扩大；P1、P3和P4点压力脉动强度随偏离度的增大而提高，而P2点压力脉动强度的变化较小.

(2) 正常情形下，P2点的最大压力脉动能量值位于叶片通过频率处；动叶异常偏离改变了P2点的时频分布，最大压力脉动能量值随偏离度的增大而增大.动叶异常偏离后，各监测点的近似熵均发生改变，尤其是在大偏离度下的变化更加显著，表明近似熵对动叶发生异常偏离有良好的表征能力.

(3) 随着偏离度的增大，叶轮中间截面上的静压时均值分布及数值均发生改变；当Δβ>20°时，在逆旋转方向上与异常动叶相邻叶片的流道也受到影响；而叶片等效应力分布随偏离度的增大变化不大，但等效应力值呈增大趋势.

(a)Δβ=0°(b)Δβ=10°

(c)Δβ=20°(d)Δβ=30°

(e)Δβ=40°(f)Δβ=50°

图8叶片等效应力分布

Fig.8Equivalent stress distribution on the surface of blade

参考文献：

[1]郭玉杰，任广印，刘占辉，等．超临界600 MW机组锅炉一次风机间歇性振动诊断[J]．热力发电，2012，41(8)：56-58.

GUO Yujie, REN Guangyin, LIU Zhanhui,etal. Diagnosis of intermittent vibration on primary air fan of supercritical boiler[J]. Thermal Power Generation,2012,41(8):56-58.

[2]XU C, AMANO R S. Unsteady pressure field investigation of an axial fan-blade unsteady pressure field measurement[J]. International Journal of Rotating Machinery,2002,8(6): 385-395.

[3]LI Yang, LIU Jie, OUYANG Hua,etal. Internal flow mechanism and experimental research of low pressure axial fan with forward-skewed blades[J].Journal of Hydrodynamics,2008,20(3): 299-305.

[4]孟丽，林丽华，吴海英，等．轴流风机后导叶三维数值优化设计方法及其应用[J]．风机技术，2014(3)：48-52．

MENG Li, LIN Lihua, WU Haiying,etal. A 3-D numerical optimization design method and its application in axial fans with outlet guide vanes[J].Fan Technology,2014(3): 48-52.

[5]刘广强，吕子强，郭宇，等．中低压轴流风机流型优化的数值模拟与试验分析[J]．流体机械，2014，42(10)：1-5．

LIU Guangqiang, LÜ Ziqiang，GUO Yu,etal. Numerical simulation of axial fan based on different circulation index of impeller[J]. Fluid Machinery,2014,42(10):1-5.

[6]桂良明，刘聪，秦明亮．动叶可调轴流双级一次风机喘振分析及对策[J]．流体机械，2012，40(8)：44-46．

GUI Liangming, LIU Cong, QIN Mingliang. Analysis and solution of surge of axial flow primary air fan with double stage adjustable movable blade[J].Fluid Machinery,2012,40(8):44-46.

[7]张磊，郎进花，王松岭．电站轴流风机旋转失速工况下的叶轮静力特性研究[J]．动力工程学报，2015，35(5)：387-393．

ZHANG Lei, LANG Jinhua, WANG Songling. Static characteristics of the impeller of an axial flow fan under rotating stall conditions[J]. Journal of Chinese Society of Power Engineering,2015,35(5): 387-393.

[8]SALUNKHE P B, PRADEEP A M. Stall inception mechanism in an axial flow fan under clean and distorted inflows[J].Journal of Fluids Engineering,2010,132(12):121102.

[9]叶学民，李鹏敏，李春曦．叶顶开槽对轴流风机性能影响的数值研究[J]．中国电机工程学报，2015，35(3)：652-659．

YE Xuemin, LI Pengmin, LI Chunxi. Numerical investigation of grooved blade tips effect on the performance of an axial flow fan[J]. Proceedings of the CSEE,2015,35(3):652-659.

[10]NHO Y C, PARK J S, LEE Y J,etal. Effects of turbine blade tip shape on total pressure loss and secondary flow of a linear turbine cascade[J].International Journal of Heat and Fluid Flow,2012, 33(1):92-100.

[11]蔡涛，周水清，王军.加环控制轴流风机叶顶间隙的分析与试验[J]．工程热物理学报，2014，35(12)：2406-2411．

CAI Tao,ZHOU Shuiqing,WANG Jun. Analysis and test on the performance of the axial fan with a ring near the blade tip on the casing[J].Journal of Engineering Thermophysics,2014, 35(12): 2406-2411.

[12]HU Binbin, OUYANG Hua, WU Yadong,etal. Numerical prediction of the interaction noise radiated from an axial fan[J]. Applied Acoustics, 2013,74(4):544-552.

[13]LEE J W, KIM Y Y. Topology optimization of muffler internal partitions for improving acoustical attenuation performance[J]. International Journal for Numerical Methods in Engineering,2009,80(4):455-477.

[14]李业，周水清，王军，等．转速对弯掠轴流风机气动噪声的影响分析[J]．工程热物理学报，2014，35(1)：51-55．

LI Ye, ZHOU Shuiqing, WANG Jun,etal. Analysis of aerodynamic noise of a swept-curved axial flow fan with different rotate speed[J]. Journal of Engineering Thermophysics,2014,35(1):51-55.

[15]陈庆光，房菲，张振东，等．对旋风机叶轮内部流场的压力脉动分析[J]．山东科技大学学报(自然科学版)，2011，30(2)：81-85．

CHEN Qingguang, FANG Fei, ZHANG Zhendong,etal. Analysis on pressure fluctuation of the interior flow field in impellers of a contra-rotating axial fan[J].Journal of Shandong University of Science and Technology(Natural Science),2011,30(2):81-85.

[16]BALLESTEROS-TAJADURA R,VELARDE-SUAREZ S, HURTADO-CRUZ J P,etal. Numerical calculation of pressure fluctuations in the volute of a centrifugal fan[J].Journal of Fluids Engineering,2006,128(2):359-369.

[17]JIRO F, TAKUYA F, YUSUKE O,etal. Measurements of minute unsteady pressure on three-dimensional fan[J].Journal of Environment and Engineering,2010,5(2): 298-310.

[18]叶学民，李新颖，李春曦．第一级叶轮单动叶安装角异常对动叶可调轴流风机性能的影响[J].中国电机工程学报，2014，34(14)：2297-2306．

YE Xuemin, LI Xinying, LI Chunxi. Effect of the first-stage impeller with abnormal blade on the performance of an axial fan[J]. Proceedings of the CSEE,2014,34(14):2297-2306.

[19]叶学民，王丰，李春曦．两级动叶异常偏离下的轴流风机性能和内流特征[J]．动力工程学报，2015，35(5)：394-403．

YE Xuemin, WANG Feng, LI Chunxi. Performance and internal flow characteristic of an axial flow fan with installation deviation in two-stage blades[J].Journal of Chinese Society of Power Engineering,2015,35(5):394-403.

[20]POSSON H, MOREAU S, ROGER M. Broadband noise prediction of fan outlet guide vane using a cascade response function[J]. Journal of Sound and Vibration,2011,330(25):6153-6183.

[21]李春曦，林卿，叶学民．单动叶安装角异常时轴流风机的噪声特性[J]．中国电机工程学报，2015，35(5):1183-1192．

LI Chunxi, LIN Qing, YE Xuemin. Acoustic characteristics of an axial flow fan with abnormal installation angle of single blade[J]. Proceedings of the CSEE,2015,35(5):1183-1192.

[22]索洛玛霍娃 T C．通风机气动略图和性能曲线[M]．北京：煤炭工业出版社，1986：336-348．

[23]王文杰，袁寿其，裴吉，等．时序效应对导叶式离心泵内部压力脉动影响的数值分析[J]．机械工程学报，2015，51(4)：185-192．

WANG Wenjie, YUAN Shouqi, PEI Ji,etal. Numerical analysis of the clocking effect on the pressure fluctuation in the centrifugal pump with vaned diffuser[J]. Journal of Mechanical Engineering, 2015,51(4):185-192.

[24]胡劲松．面向旋转机械故障诊断的经验模态分解时频分析方法及实验研究[D]．杭州：浙江大学，2003．

[25]胡红英，马孝江．局域波近似熵及其在机械故障诊断中的应用[J]．振动与冲击，2006，25(4)：38-41．

HU Hongying, MA Xiaojiang. Application of local wave approximate entropy in mechanical fault diagnosis[J]. Journal of Vibration and Shock,2006,25(4):38-41.

Numerical Analysis on Pressure Fluctuation of an Axial Flow Fan with Abnormal Installation Angles of a Single Blade

YEXuemin,DINGXueliang,LIChunxi

(Key Lab of Condition Monitoring and Control for Power Plant Equipment of Ministry of Education,North China Electric Power University, Baoding 071003, Hebei Province, China)

Abstract：Taking the OB-84 variable-pitch axial-flow fan as an object of study, an unsteady calculation was conducted on the internal dynamics and fan performance under different deviation degrees of a single blade, so as to obtain the time-domain and time-frequency characteristics, and the distribution of time-averaged static pressure and equivalent stress. Simulation results show that both the pressure signal and pressure fluctuation energy at each monitoring point exhibit unusual features with abnormal installation angles of blade, especially the most obvious changes at impeller outlet. The impacts of abnormal blade installation on time-domain and time-frequency characteristics are enhanced with rising deviation degrees, resulting in increased intensity of pressure fluctuations. The approximate entropy at each monitoring point changes obviously with large deviation degrees, indicating good characterization ability on the abnormal blade installation. Remarkable changes are found in the distribution and values of time-averaged static pressure, but the equivalent stress only varies obviously in values.

Key words：variable-pitch axial-flow fan; deviation degree; abnormal installation angle; pressure fluctuation

收稿日期：2015-07-13

基金项目：河北省自然科学基金资助项目(E2012502016)；中央高校基本科研业务费专项基金资助项目(13MS98)

作者简介：叶学民(1973-)，男，河北邢台人，教授，博士，主要从事流体机械、流体动力学理论及应用和新能源技术等方面的研究.

文章编号：1674-7607(2016)05-0395-09中图分类号：TK223.26

文献标志码：A学科分类号：470.30

电话(Tel.)：13932203443;E-mail：yexuemin@163.com.