知识收敛与思维发散——由一道习题教学想到的

□荀步章



知识收敛与思维发散
——由一道习题教学想到的

□荀步章

【摘要】数学家波利亚说:“模型的识别能力是学生解题能力的重要组成部分。”教材中的每一道习题，以单一型为主，学生不容易发现一般规律，却认为自己发现了“规律”。问题探究过程不仅仅是告诉，更需要儿童亲身经历，在实践探索过程中感受数学思维的魅力，积累基本的数学思想方法，提升数学素养。

【关键词】模型；习题；探究

数学家波利亚说：“模型的识别能力是学生解题能力的重要组成部分。”教材中的每一道习题，以单一型为主，学生不容易发现一般规律，却认为自己发现了“规律”。问题探究过程不仅仅是告诉，更需要儿童亲身经历，在实践探索过程中感受数学思维的魅力，积累基本的数学思想方法，提升数学素养。如“解决问题的策略—转化”一道习题教学：

师：观察这道算式有什么发现？

生：分母每次都乘2，分子都是1。

生：后一个分数是前一个分数的一半。

师：如果继续加一个数，加多少？

生：化成小数，0.5+0.25+0.125+0.0625=0.9375。

生：可以化成小数，0.5+0.25+0.125+0.0625+0.03125= 0.96875。

生：很麻烦！

师：数学家华罗庚说“数形结合百般好”，如果借助图形解决这个问题会更加简便。电脑演示，把一个正方形平均分成两份，每份用表示，再把剩下的图形平均分成两份，每份占正方形的……，如下图，计算，怎么计算简便？

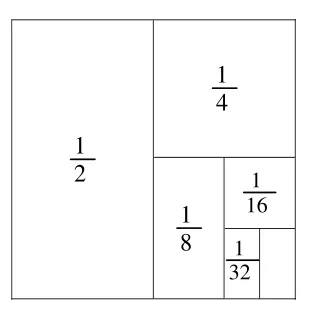
生：把正方形面积看作单位“1”，用单位“1”减去最后一小块空白部分面积，就是所求算式的结果。

生：就是用1减去最后一个分数等于结果。

师：真了不起！想到了这么好的一个办法。还能想到什么呢？

师：分组来探究一下，是否存在规律？三个小组分别计算下面三道题：（1）

（汇报交流。）

师：第1题有什么规律？

生：后一个分数是前一个分数的一半。

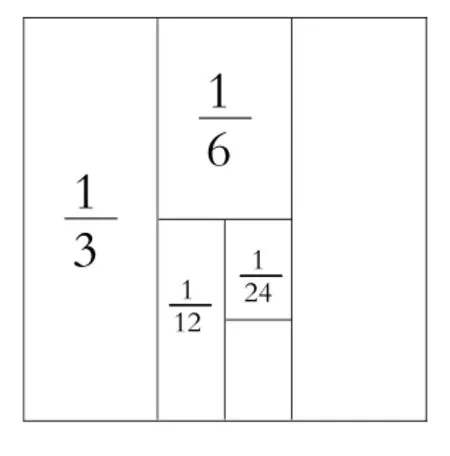
生：第2题后一个加数也是前一个加数的一半。

师：观察这一组问题，有什么发现？小组交流一下，再汇报。

生：有规律的一组数，后面的数都是前一个数的一半。

生：都可以用通分方法计算。

生：用减法计算比较简便。

生：都是用几分之二减去这组数中最后一个数。

生：不对，第一个是用1减的。

（全班学生鼓掌。）

师：计算一道复杂的加法算式，借助画图，从反面入手，算减法更简单。数形结合，帮助我们思考，从而找到更加简便的计算方法。

教材只给出这一道习题，教师二度开发教材，“真是这样吗？举例验证一下”，分小组探究同质问题，发现规律的本质，建立一类数学模型。学生在加法与减法、通分与画图、数的规律与形的规律等方面进行比较，沟通问题之间的相互联系，提升了数学思维能力。

在问题探索过程中，知识收敛与思维发散形成对比，一道问题表面看是用单位“1”减去最小空白部分，但引入同质问题后，可以更清楚地发现，用几分之二减去最后的空白部分，知识点之间是紧密联系的。从学生探索规律本身来看，思维挑战渐增，为学生后续学习数学提供“模型”。探究一个数学结论的过程不是一帆风顺的，而是要经历多个类似问题的反复研究，才能接近本质，学生的思维是灵活的，开放的，更是增质的，充盈的。

一、知识收敛与思维发散的意义

当今社会，知识量激增，数学教学中要考虑如何设计好这门学科中的“桩”“柱”“梁”，即如何突出主干内容。就象造房子，原来老房子是靠砖块一块一块地砌上去的，这些砖块就好比是知识与概念，这样的房子造不高也造不牢。现在的房子是框架式的，依靠几个支柱把房子造高、造牢，砖块仅仅起到一些隔离的作用。知识收敛指的是在教学中向学生介绍知识、概念时，不要过多，而要抓住精要部分，有所选择的突出核心内容。一是体现主干性，知识点要围绕教学核心目标补充与展开；二是体现同质性，面对同一个知识解读，借助一类同质知识类比发现规律；三是体现探究性，课堂教学要让学生经历知识发生的过程，让学生探究和思考。

心理学家吉尔福特认为“思维发散具有流畅，变通和独特三个特征”。思维发散指的是在问题解决过程中思维呈现的状态，一是体现方向性，对同一问题研究不是单向线性的，而在不同层面上思考与挖掘；二是体现多层性，问题的探究过程不停留于既定的预设，要不断提出新问题或发现新结果的思维方式；三是体现开放性，学生思维状态表现灵动、巧妙与创新的特征，思路广阔，对已有经验的改造层层递进。思维发散性在思维内容上具有变通性，引申旧知，发现新方法等具有积极的开拓作用。布鲁纳所提倡的发现法，其用意也在于使学生成为知识的发现者，培养学生的发现性思维，这里的发现也是指教育意义上的广义创造性。就当前小学数学教学而言，学生还谈不上严格意义上的创造，但却有大量的“再发现”的内容与机会。

二、知识收敛与思维发散的策略

知识收敛与思维发散表现在课堂中具有极大的相关性。课堂要充分突出知识主干，削弱旁枝，遵循课标与教学目标，有效利用学生已有旧知，尽可能展示学生的数学思考过程，发展学生的数学思维。

1.教师多讲转向学生多展

教师的必要引导不可缺少，更多的知识是儿童在已有旧知中生长出来的，他们对新知有独特的内心体验，同龄人之间的思维碰撞更易产生思维火花。在“最近发展区”中的知识是单面的，通过不同个体展示，逐渐走向立体的知识块。如“解决的问题策略—列表”教学：

（师出示主题图。）

师：课前同学们进行了预学，现在进行全班展示交流。

生：我选择摘抄全部条件和问题的方法，“小明买3本笔记本，用去18元，小华买5本笔记本，用去多少元？”后来省略了一些文字，“小明3本用18元，小华5本用？元”。

生：我用画表格方法整理：

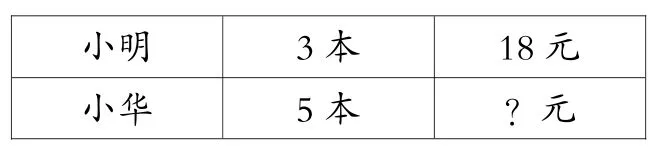
生：我用画图的方法，一本笔记本画一个框。

小明□□□18元

小华□□□□□？元

生：我用画线段图的方法。

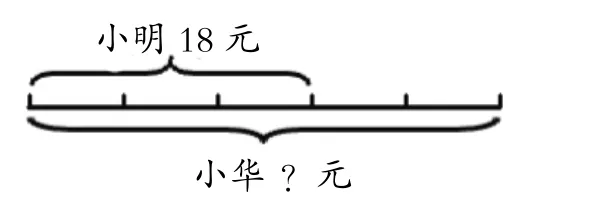
生：我用画箭头图的方法。

小明3本→18元

小华5本→？元

……

学生经过课前预学，有准备地走进课堂，教师要主动“让学”，让学生走上讲台，展示预学情况。每一位学生的理解和方法是多样的，有摘抄全部条件和问题的方法，画表格方法，画图的方法，画箭头图等，个体产生成就感、满足感。让全班学生交流不同的整理方法，使学生充分体验到解决问题策略的多样性，对培养学生发散性思维大有裨益。

2.一题一问转向一题多问

一题一问对学生而言，知识点联系不够，不能有效结成知识网，培养学生思维的整体性。一题多问通过转化旧知达到解决新问题目的，是培养学生发散思维，提高思维品质的重要方法。例如，“解决问题的策略—替换”教学：

师：有两杯果汁，根据它们的容量，你发现什么？

生：大杯容量比小杯多160毫升，小杯容量比大杯少160毫升。

生：大杯和小杯容量共320毫升。

出示探究问题：小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。小杯和大杯的容量各是多少毫升？

让学生独立解决，发现条件不足，分别补充三个条件，依次探究解决问题的不同类型：①小杯的容量是大杯的②大杯容量比小杯多160毫升；③大杯和小杯容量共320毫升。

观察两杯大小不等的果汁，说一说它们之间的数量关系，学生能发现倍数关系、和差关系，为探究问题准备素材，从整体上引领探究全过程。一题多问、一题多解可充分发挥已知知识和信息的作用，从多方向、多角度思考同一问题，更加明确地体现了发散思维的训练和创造思维的培养。

3.套用公式转向运用公式

课堂练习设计，一般借用教材中的“试一试”，缺乏对核心目标的追问。多边形的面积教学，除一般的公式练习，更应侧重于对公式的灵活运用，帮助学生深度理解和灵活运用。例如，“平行四边形的面积”教学后：

出示图1，一个湖泊外围框一个平行四边形，问湖泊的面积大约是多少？

图1

生：用130×110。

师：可以吗？

生：可以。

师：很可以吗？

生：用平行四边形把湖泊框住了，平行四边形的面积比湖泊的面积大了一些。

出示图2，如果在湖泊里面有一个平行四边形，问湖泊的面积大约是多少？

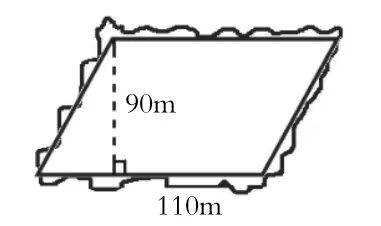
图2

生：如果用110×90计算，应该比湖泊小一些。

师（顺势出示图3）：这样怎么样？

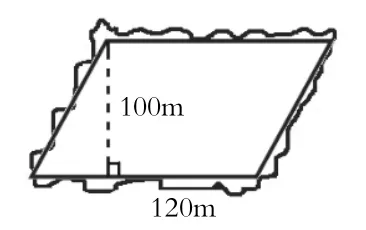
图3

生：用120×100计算，更加合理。

师：“合理”用的好，古人都知道这个道理，用“出入相补”来描述。

生：把多出来的部分补给少的。

师：这个平行四边形的底120米，高100米，面积大约是多少平方米？

生：120×100=12000 (平方米)。

师：画等号，还是约等号？

生：约等号。

师：从120×100等于12000平方米，本身有没有大约？

生：没有。

师：嗯，动脑筋想一想，是谁与谁在约，12000平方米代表标准平行四边形的面积，用这个标准平行四边形的面积约等于湖泊的面积，在答句中写上大约，列式中不写约等于。

教者精心设计了一道求湖泊面积的问题，把湖泊面积看成一个平行四边形面积，怎样看？部分学生认知不清晰，先在湖泊外围“套”一个平行四边形，面积太大；接着在湖泊里面“嵌”一个平行四边形，面积略小；最后采用“出入相补”的平行四边形“放”上面，面积最“准”。通过这三个平行四边形面积的比较，学生深刻感受到，估计也要讲究策略，提高了思维的深刻性，还渗透了无限逼近的思想。用不用“约等于号”部分学生也混淆不清，抓住了问题本质，谁与谁在“约”，不出现张冠李戴，揭示了等量之间的替代关系。

4.死记硬背转向体验过程

传统教学过程，注重死记硬背，大量练习，缺少对知识过程经历，缺少关注学生在学习知识过程中创造性解决问题的能力培养。知识在体验和感悟中形成，在问题解决中发展数学思维。例如“圆的周长”教学：

（出示一个正方形和一个圆形。）

师：这两个图形，给你一把直尺，测量它们的周长，你愿意测量哪一个？为什么？

生：我愿意测量正方形。因为正方形的边是直的，好测量，圆的边线是弯的，不太好量。

师：如果老师想为难你们，就用直尺量出圆的周长，敢挑战吗？

（出示一个荧光圈。）

师：这个荧光圈的周长怎样测量？

生：把接头拔下来，拉直了，然后量一量。（教师实物演示过程）

师：真不错，已经想到把弯曲的荧光圈转化成直直的线段了。

（出示一个飞镖盘。）

师：这个飞镖盘，不能拉直，怎么办？

生：可以用线绕一圈，然后量出线的长度，就是飞镖盘的周长。

生：把飞镖盘在直尺上滚一圈，看一看滚多远，就是它的周长。

师：这些办法有一个共同特点，就是“化曲为直”。

（出示一幅摩天轮图片。）

师：这个摩天轮，用拉、剪、滚、绕的方法适合吗？怎么办？

（再次出示刚才的正方形和圆形。）

师：正方形的周长与边长有关，圆的周长可能与什么有关？

生：圆的直径、半径。

（课件演示，引导观察。）

师：三个直径不同的车轮，同时向前滚动一周，你发现了什么？

生：直径越大，圆的周长就越大，直径越小，圆的周长就越小。

生：半径越大，圆的周长就越大，半径越小，圆的周长就越小。

师：正方形周长是边长的4倍，猜想一下，圆的周长大约是直径的多少倍？

……

教者把圆形和正方形对比探究，“你愿意测量哪一个？”正方形的边线是直直的，容易测量，而圆形边线是弯弯的，不容易测量。在测量方式上，“用拉、剪、滚、绕的方法适合吗？”正方形周长可以根据一条边的长度直接计算，圆形需要想办法“化曲为直”，探索圆与正方形周长时，让学生经历“化曲为直”的思考过程。在关系研究上，“正方形的周长与边长有关，圆的周长可能与什么有关？”让学生先猜想，再逐步去掉不合理的答案，范围由大到小，研究由粗到细，慢慢触摸“本质”。让学生发现规律，提出猜想，感受多样化的解决策略，在合作与交流，创生与探索中寻求突破。

综上所述，知识收敛方能有效地进行思维发散，这就要求教师认真钻研教材，根据学生实际抓住重点，抓主干内容，合理大胆地进行教材处理。教师应“拿得起，放得下”，“拿得起”就是敢于把有利于培养学生思维和能力的题材用于教学，善于挖掘教材的内涵。“放得下”就是教师能大胆地把一些作用不大、费时太多的内容处理掉，把许多重复的操练减下来，让学生学得轻松、愉快、高效。

（编辑：赵悦）

中图分类号：G623.5

文献标识码：A

文章编号：1671-0568（2016）10-0053-04

作者简介：荀步章，江苏省宝应县实验小学教师，中学高级教师，扬州市特级教师，江苏省“333”工程高层次人才培养对象。生：