气液两相多组分非等温渗流的数学模型

何　增，田　宙，王铁良

(西北核技术研究所，西安710024)



气液两相多组分非等温渗流的数学模型

何增，田宙，王铁良

(西北核技术研究所，西安710024)

摘要：通过分析气液两相在多孔介质中的相互作用过程，建立了一套描述两相多组分非等温渗流的数学模型。所建立的控制方程中，既包括对流、弥散和源汇作用，也包括非达西流动、水气转变以及辐射传热等高温高压环境下的特殊物理过程。提供了一套完整的使控制方程封闭的本构关系，并推导了比能和比焓的计算公式。利用本文模型对地下爆炸气体的迁移过程进行了数值模拟。结果表明：与气相渗流模型相比，该模型可以更合理地描述气体在地质介质中的输运行为。

关键词：两相渗流；非等温流动；数学模型；本构关系；气体输运

两相非等温渗流技术在环境保护、生物科学、能源工业等领域广泛应用[1-2]。两相渗流的研究以渗流力学为基础，与岩石力学、表面物理、传热学等学科交叉，一直是渗流领域的研究热点。国内外学者开展了大量的研究工作，并建立了许多理论模型。例如，美国劳伦斯·伯克利国家实验室Pruess等开发的TOUGH2系列程序[3-4]可用于模拟孔隙-裂隙介质中多相多组分的非等温流动，主要应用于地热存储、核废料处置、环境评估及修复等领域，如文献[5]利用该程序对内华达试验场尤卡山中的多相示踪剂输运问题进行了试验场尺度的研究，Class等建立了低压下适用于10～300℃的三相三组分非等温渗流模型[6]，并进行了验证与确认。此外，常见的程序还有美国劳伦斯·利弗莫尔国家实验室Nitao等研制的NUFT程序[7-8]、斯图加特大学Helmig等发布的MUFTE-UG程序[9]等。国内刘昌军推导了不可压缩水气两相渗流的微分方程，并对降水入渗下饱和-非饱和水气两相渗流作了深入探讨[10]。刘晓丽等基于岩体渗流水力学和多相渗流力学理论，建立了不可压缩水气两相渗流与双重介质变形的流固耦合数学模型[11]。黄朝琴等建立了不可压缩两相渗流的离散裂隙型模型[12]，研究了裂隙性油藏的注水开发过程。

对比国内外相关研究可以看出，国内研究所使用的模型较为简单，未考虑气体的压缩性和非等温效应。本文综合考虑气液在多孔介质中的相互作用过程，建立了描述气液两相多组分非等温渗流的数学模型，包括控制方程和本构关系两部分，并以此为基础研究了地下爆炸后气体的迁移行为。

1气液两相多组分非等温渗流的数学模型

两相为液相(l)和气相(g)，用α表示相态；组分为水(w)、空气(a)和示踪物(t，地下爆炸的示踪物一般为一氧化碳)，用κ表示组分。本文将空气简化为单一组分的气体。控制方程包括质量守恒方程、运动方程和能量守恒方程，为了使方程封闭，还应该补充相应的本构关系。本文模型可用来描述任意多组分气体，这里以三组分为例进行说明。

模型的适用条件为：1) 空气和示踪物均不溶于液态水；2) 在气液两相共存时，水蒸气为饱和蒸汽；3) 气体组分均满足理想气体状态方程；4) 固体骨架和液态水不可压缩；5) 不考虑毛细压力滞后效应。

1.1控制方程

以组分为研究对象可以很方便地得到质量守恒方程，而不必考虑组分在相间转化的细节。相作为一个整体是一起运动的，故运动方程需要分相建立。采取局部热平衡假设构建能量方程：在一个代表性单元内，流体和骨架具有相同的温度。质量和能量转移的途径在液相中有对流迁移与源汇作用，在气相中还包含水动力弥散效应。

1.1.1质量守恒方程(连续性方程)

水在气相和液相共存，而空气和示踪物只存在于气相。因此，水的连续性方程为

(1)

空气和示踪物的连续性方程为

(2)

其中，φ为多孔介质孔隙度；Sl、Sg分别为液相、气相的饱和度；ρl、ρg为液相、气相的密度；Xg(κ)为组分κ在气相中的质量分数；vl、vg分别为液相、气相的渗流速度；Dg(κ)为组分κ在气相中的水动力弥散系数；q(κ)为组分κ的质量源汇项。

对弥散通量，存在如下制约关系：

(3)

1.1.2运动方程

根据达西定律[1]，多孔介质中液相和气相的运动方程为

(4)

其中，K为固有渗透率张量；kr,α为α相的相对渗透率；μα为α相的动力黏度；pα为α相的压强；g为重力加速度矢量。

在流速较大时，许多学者对达西定律提出了修正方案[2]。对于多相非达西流动，Forchheimer方程的形式为[14]

(5)

其中，η为固有通过率；ηr,α为α相的相对通过率；β为Forchheimer系数，其与固有通过率的关系为β=1/η。

式(5)右端的第3项表示惯性力的贡献。为了表征流动偏离达西定律的程度，定义第3项与第2项之比为Forchheimer数[15]

(6)

在应用时，首先由达西定律求出速度vα，再由式(6)计算Foα。将Foα与其判断标准Foc进行比较，如果Foα>Foc，则用式(5)重新求vα。

1.1.3能量守恒方程

考虑对流传热、弥散传热以及热传导，建立能量守恒方程为

(7)

其中，uα为α相的比能；hα为α相的比焓；hg(κ)为处于气相的组分κ的比焓；λp为多孔介质的表观热导率；qh为能量源汇项；ρs和us分别表示固体骨架的密度和比能，下标s表示固体骨架。

研究表明，在温度变化范围较大时，忽略辐射传热将引起较大误差[16]。辐射传热等于辐射热流密度φ与面积的乘积[17]，φ的表达式为

(8)

其中，T为温度；为介质黑度，大部分非金属材料的黑度在0.85～0.95之间，本文取=0.9；C0为黑体辐射系数。

1.2本构关系

为使上述控制方程封闭，还需要提供相应的本构关系。本节将给出具体的本构关系，重点对比能和比焓的计算公式进行推导。需要说明的是，部分参数(如相对渗透率)的计算有多种经验公式，本文只给出一种。

1.2.1约束性条件

气相和液相的饱和度满足

(9)

气相中各组分的质量分数满足

(10)

1.2.2气体的状态方程

采用理想气体状态方程描述气体。气体的总压力等于各组分气体的分压之和：

(11)

其中，R(κ)为组分κ的气体常数。在气液两相共存时，假设水蒸气为饱和蒸汽，即水蒸气的分压等于相同温度下的饱和蒸汽压。

(12)

本文使用国际水及水蒸气性质协会(TheInternationalAssociationforPropertiesofWaterandSteam,IAPWS)推荐的水的饱和蒸汽压公式[18]。

1.2.3水动力弥散系数

水动力弥散系数包含机械弥散和分子扩散两项，其分量计算公式为[5,19]

(13)

其中，αT、αL分别为介质的横向、纵向弥散度；τ为介质的弯曲因子；Dd(κ)为组分κ在气相中的分子扩散系数。

利用Wilke方法[13]，通过双组分扩散系数得到多组分扩散系数Dd(w)和Dd(t)为

(14)

其中，Dd(w-a)、Dd(w-t)和Dd(a-t)分别为水蒸气-空气、水蒸气-示踪物及空气-示踪物的扩散系数；xg(w)、xg(a)、xg(t)分别为组分w、a、t的摩尔分数。在缺乏观测资料时，双组分扩散系数一般采取Wilke-Lee方法进行估计[20]。空气的弥散系数Dg(a)可根据限制条件式(3)得到。

Millington和Quirk提出的弯曲因子的表达式为[21]

(15)

1.2.4相对渗透率与相对通过率

相对渗透率kr,α描述的是多相渗流中有效流动面积减小产生的影响，一般将其简化为有效饱和度Se的函数，如常用的相对渗透率表达式为[14,22]

(16)

本文考虑毛细压力的情形[22]，取n=3。有效饱和度Se的定义为

(17)

其中，Sres,l和Sres,g分别为l相和g相流体的残余饱和度。类似地，相对通过率的常用表达式为[14]

(18)

文献[14]推荐m的取值可为3，5，6，本文取m=3。

1.2.5动力黏度

混合气体的黏度与其成分有关。本文采用Wilke方法[20]计算N组分气体的黏度

(19)

其中，φij的计算公式为

其中，M(i)表示组分i的分子量。

1.2.6毛细压力

气液两相的压差称为毛细压力pc，即

pc=pg-pl

(20)

通常将毛细压力简化为有效饱和度的函数，如Leverett给出的关系式为[23]

(21)

其中，σ为气液两相间的表面张力。

1.2.7比能和比焓

IAPWS协会选定水三相点的液相水作为参考状态。三相点液相水的参数为[18]

(22)

三相点水蒸气的比焓为[18]

(23)

本文采纳上述规定，推导比能和比焓的计算公式。

假设液态水不可压缩，其比能为

(24)

其中，cl为液态水的比热容；Δul=cl·Tt。式(24)最后的近似条件是在所研究的温度范围内，比热容近似为常数。液态水的比焓为

(25)

水蒸气的比焓为

(26)

其中，Δhg=cp,g(w)·Tt-hg,t(w)。水蒸气的比能为

(27)

其中，ug,t(w)=hg,t(w)-RwTt为水蒸气在三相点的比能；Δug=cv,g(w)·Tt-ug,t(w)=Δhg。式(27)的推导利用了理想气体比热容的性质，即cp,g(κ)-cv,g(κ)=R(κ)。

根据在同一温度下两种物质的比能之差与参考点无关的性质，可得气相组分κ的比能为

(28)

(29)

固体骨架的比能为

(30)

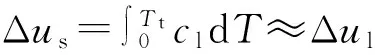
在得到各组分的比能和比焓后，混合气体的比能和比焓分别为

(31)

在常温下，气体组分κ的比热容为

(32)

其中，γ为比热比。对于水蒸气，γ(w)=4/3；对于空气，γ(a)=7/5。示踪物的比热比与其性质有关，如γ(CO)=7/5。

1.2.8热导率

平行模型[13]将多孔材料等效为相互平行的圆柱形孔隙通道，假设热流方向与多孔孔隙通道平行，则多孔介质的表观热导率为

(33)

2计算结果与讨论

采用上节模型，编制了二维柱对称坐标系下求解气液两相非等温渗流的计算程序。下面利用本文模型研究地下爆炸气体的输运问题，并将计算结果与文献[24]建立的气相渗流模型的结果进行比较，对两种模型所得结果的异同性进行解释。

在处理水蒸气-液态水的相变时，气相渗流模型[24]假设水蒸气在[Tb-ΔT,Tb+ΔT]间均匀液化，其中，Tb=373.15 K为水在1.01×105Pa的沸点，ΔT一般取为10 K。该模型没有给出相变引起的质量和能量源汇项，也未更新水蒸气和空气的份额变化。

2.1计算条件

假定在半径为7 m的空腔中，初始时刻充满了水蒸气、空气和一氧化碳，质量分别为2.40×103， 3.65×103， 5.18×103kg， 气体均匀分布， 温度为2 000 K。研究域(含空腔)是半径为86 m的球体，初始时刻与外界环境达到平衡。外界环境不含一氧化碳，气体密度为1.02 kg·m-3，温度为293.15 K。计算参数如表1所列。

表1　计算参数

2.2数值方法

图1为网格剖分示意图，计算区域为球形。任意点(θi,rj)实际代表图中所示的虚线圆圈。坐标原点位于空腔中心，图中的红圈代表空腔壁面，黑色网格代表多孔介质。研究表明，空腔区域可等效为孔隙率为1、渗透率为相邻多孔介质的渗透率与孔隙度之比的多孔介质[25]。采用交错网格的方式存储物理量，即只有速度位于网格界面，其他物理量均位于网格中心。

图1网格剖分示意图Fig.1Schematic diagram of the grid

对运动方程，使用中心差分法离散，其中，对相对渗透率与黏度之比采用迎风格式；对质量和能量守恒方程使用有限体积法离散，其中，对对流项采用迎风格式，对扩散项采用中心差分格式。数值计算中还需要处理参数在界面处的等效值。例如，根据文献[19]，当运动方向与界面平行(或垂直)时，界面处的等效渗透率为相邻边界渗透率的加权平均值(或调和平均值)。

2.3结果与分析

2.3.1600s时的物理量分布

图2给出了600s时本文模型和气相渗流模型[24]的计算结果。可以看出，气相压强、气相密度和渗流速度的分布基本吻合，因为此时空腔内尚未发生气液转变，未更新组分份额的影响也不太显著。示踪气体的质量分数在空腔内吻合是由于对流占主导地位，即气体组分几乎是以相同的比例运动的。渗透到多孔介质内的高温气体迅速降低到常温，根据式(12)，水蒸气的密度将降低、质量分数将相对减小，相应的空气和示踪气体的质量分数将增加。随着时间的推进，液态水开始出现，气相份额的变化逐渐凸显，两种模型的差异越来越大，如图3所示。

2.3.2空腔内和r=7.5m处物理量的时间历程

图4和图5分别为空腔内和r=7.5m处物理量的时间历程。图4表明，在1.25×103s后，两种模型的计算结果才有显著差异，此时本文模型开始出现液态水，对应的温度为393.15K，水蒸气分压为1.99×105Pa，而气相渗流模型[24]的相变发生在1.42×103s。液化释放的潜热将减缓温度下降速度，故本文给出的空腔温度更高。气相渗流模型的相变过程非常快，使得空腔壁面气体流速迅速降低(见图3(d))，故得到的气相密度更大。此外，根据本文模型，在相态发生变化后，水蒸气的质量分数减小，空气和示踪气体的质量分数增加。图5表明，在r=7.5m处，两种模型给出的结果基本吻合。例如，温度的差异始终在3K之内，这与空腔的温度变化范围相比可以忽略。

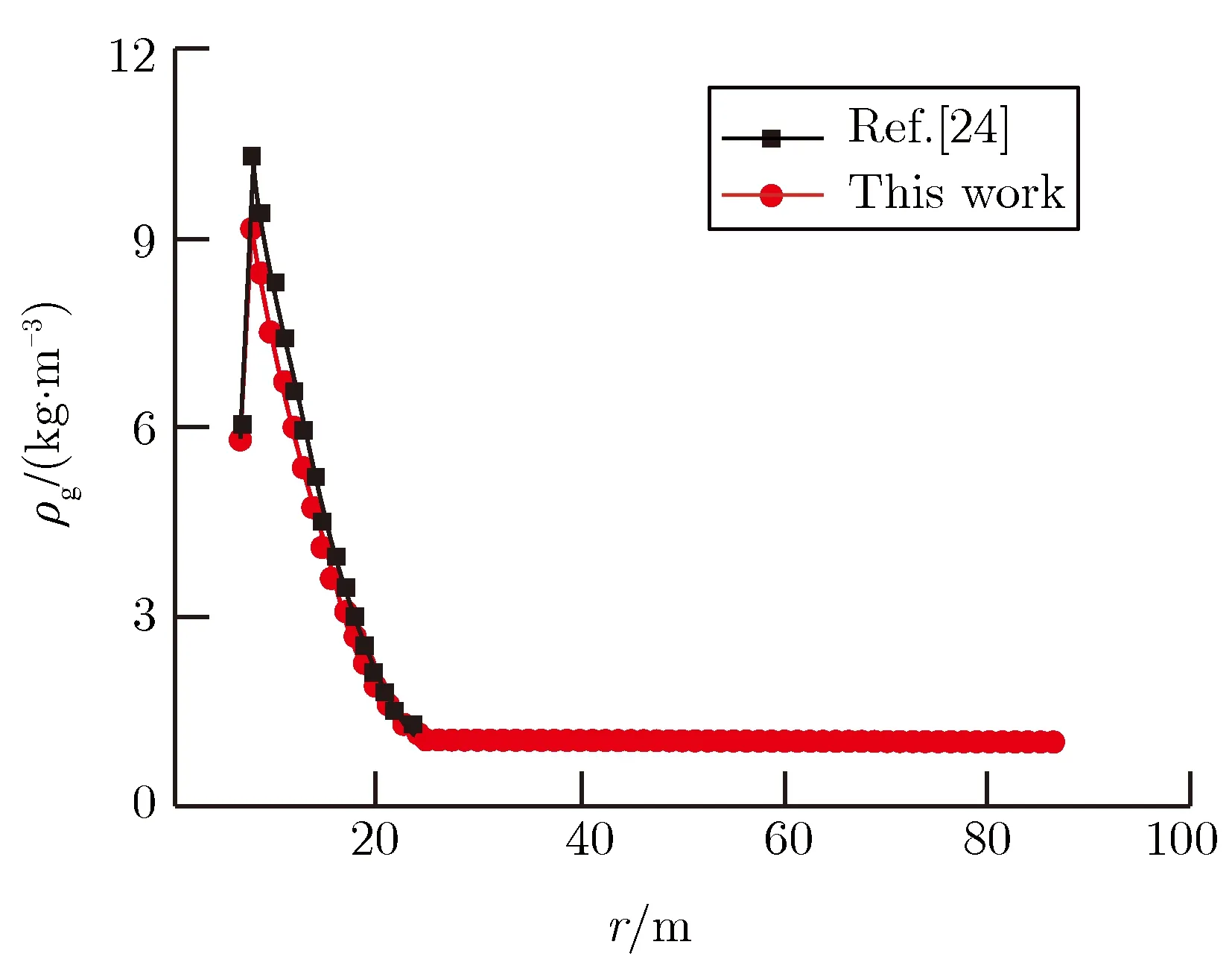
(a)Pressureofthegasphase(b)Densityofthegasphase

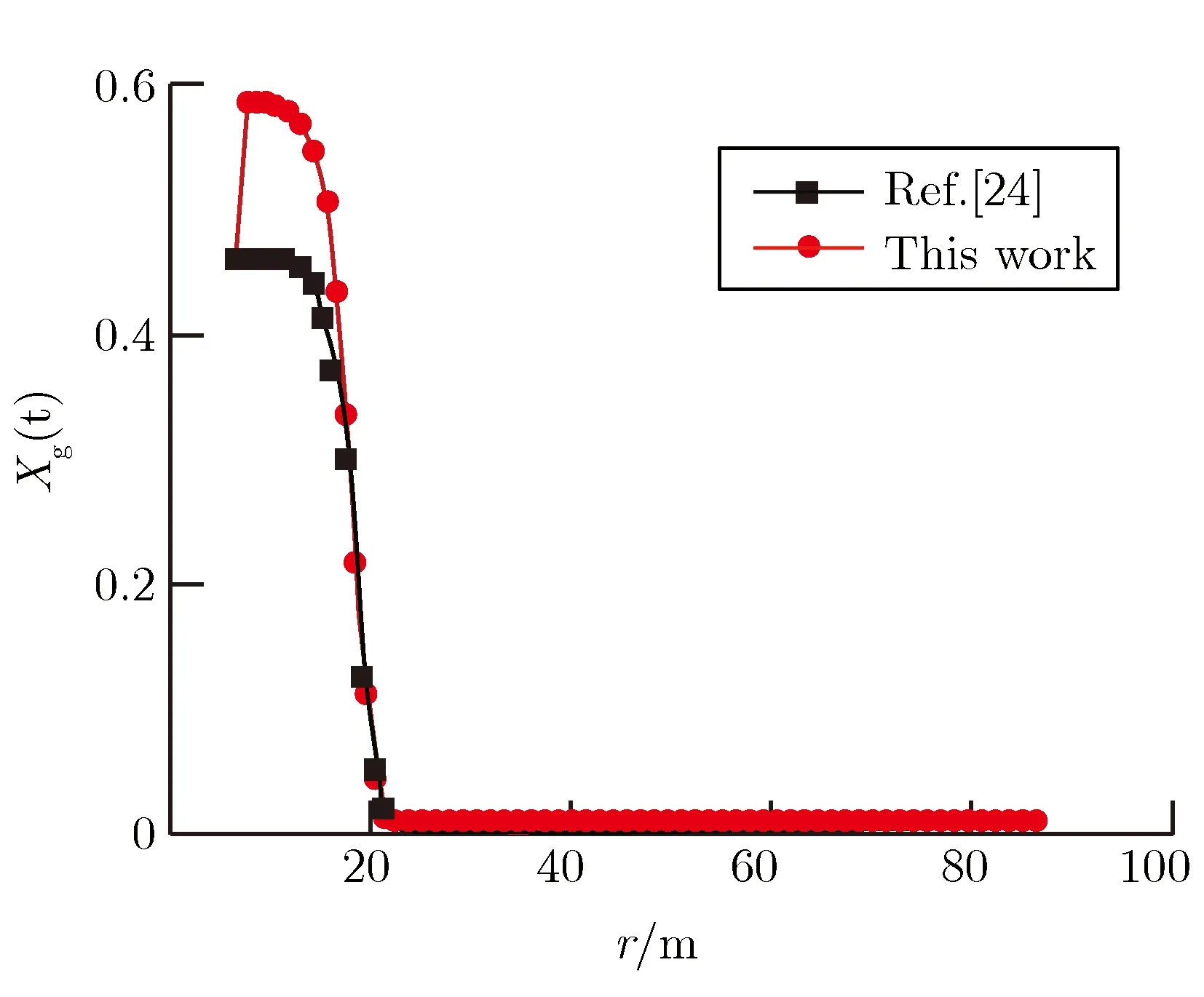
(c)Massfractionofgastracer(d)Darcy’svelocityintheradialdirection

图2t=600s时的各物理量分布

Fig.2Distributionofphysicalquantitiesatt=600s

(a)Pressureofthegasphase(b)Densityofthegasphase

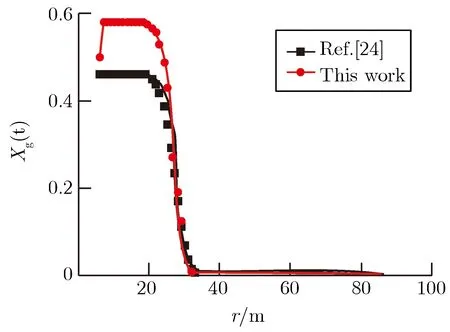
(c)Massfractionofthegastracer(d)Darcy’svelocityintheradialdirection

图3t=3 600s时的各物理量分布

Fig.3Distributionofphysicalquantitiesatt=3 600s

(a)Pressureofthegasphase(b)Densityofthegasphase

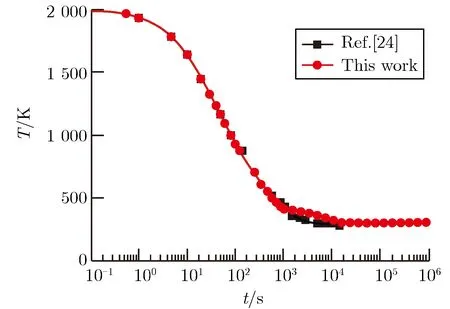
(c)Massfractionofthegastracer(d)Temperature

图4空腔内各物理量的时间历程

Fig.4Timehistoryofphysicalquantitiesinthecavity

(a)Pressureofthegasphase(b)Densityofthegasphase

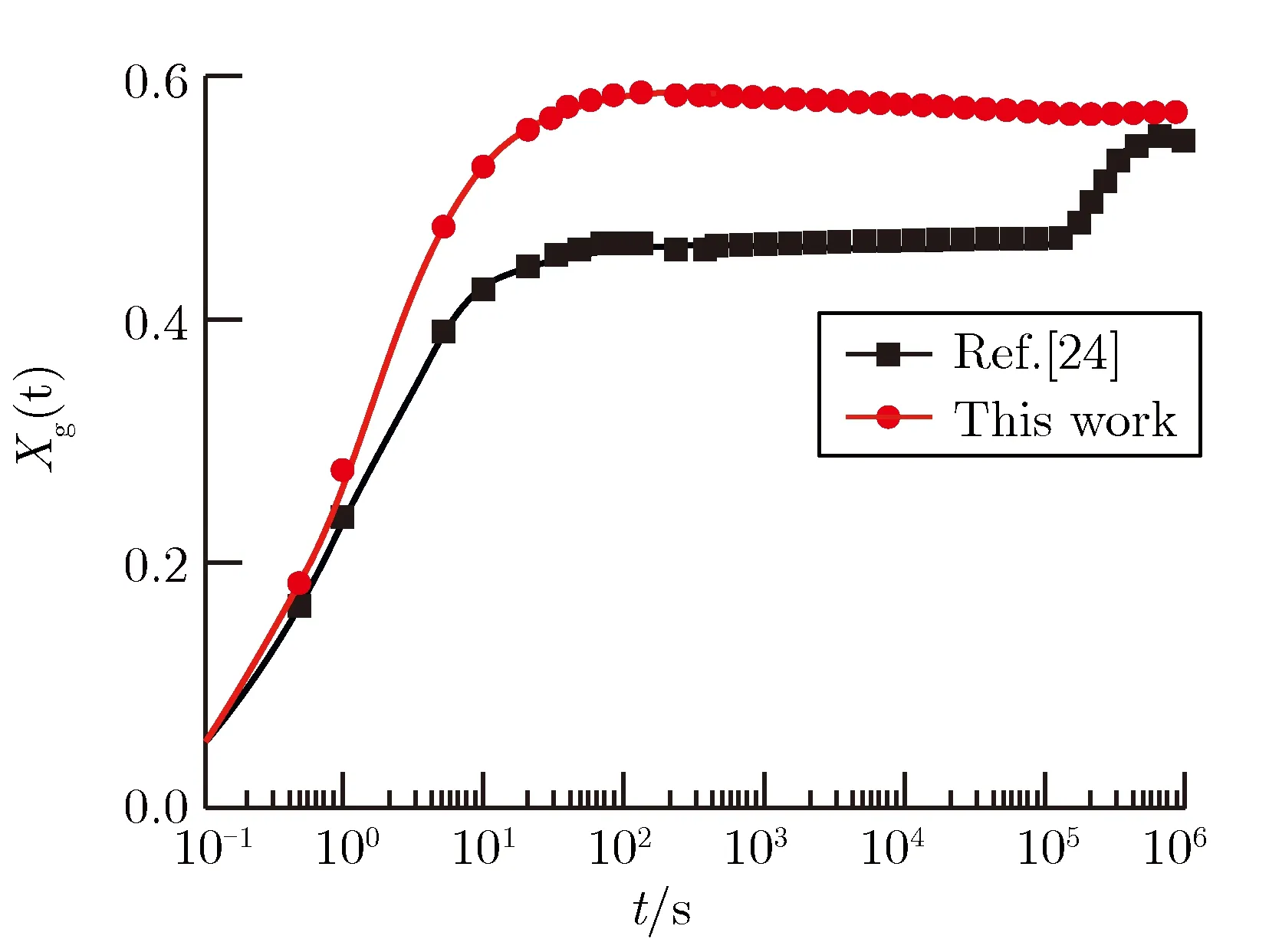
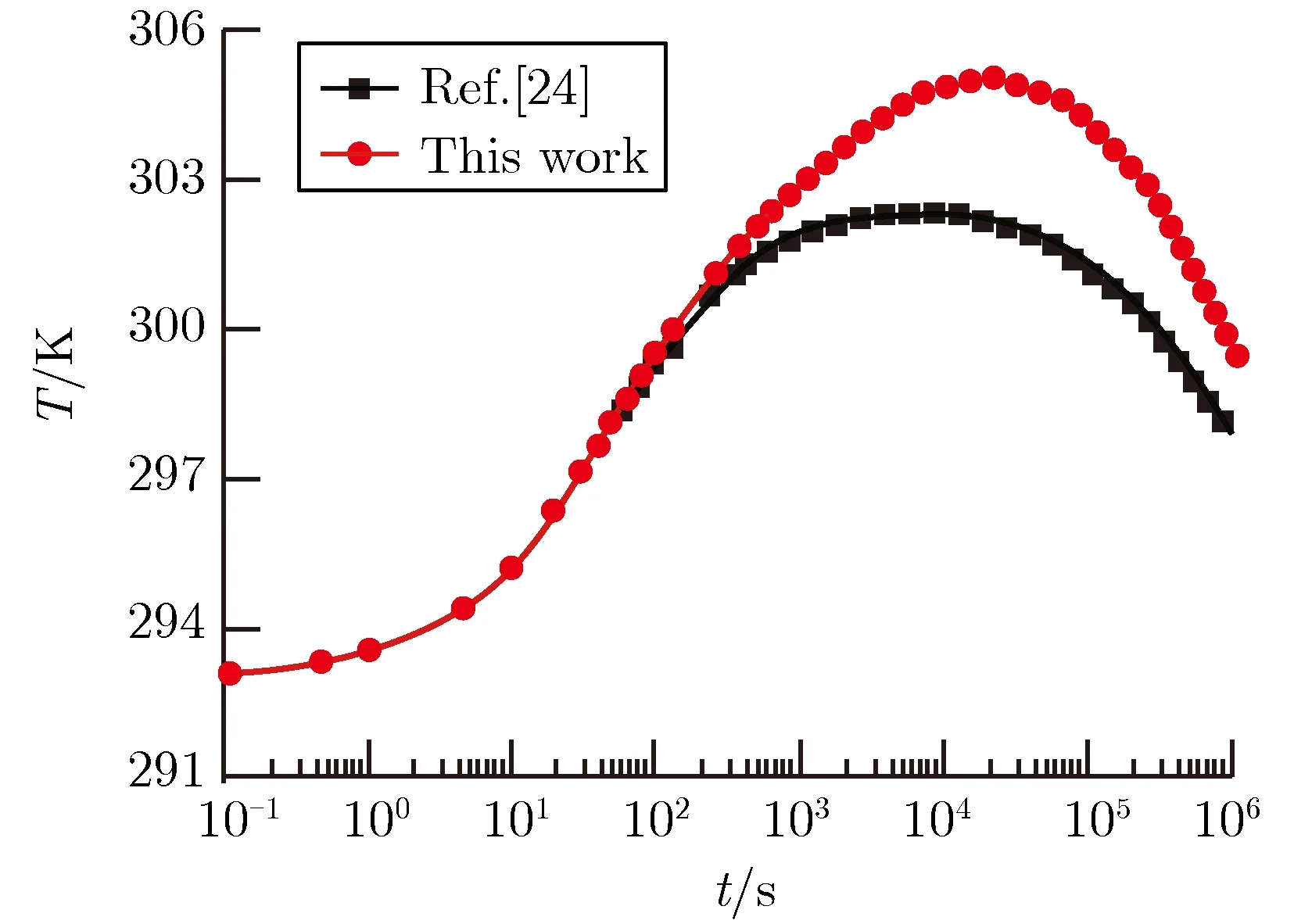
(c)Massfractionofthegastracer(d)Temperature

图5r=7.5m处各物理量的时间历程

Fig.5Timehistoryofphysicalquantitiesatr=7.5m

3小结

通过分析气液两相在多孔介质中的相互作用过程，建立了描述两相多组分非等温渗流的数学模型。其中，针对高温高压环境，考虑了非达西流动、水气转变以及辐射传热等特殊过程，且提供了一套完整的本构关系使控制方程封闭。应用该模型模拟了爆炸气体的迁移行为，并与气相渗流模型[24]的计算结果进行了比较。对比结果表明，本文模型可以更合理地描述空腔内的气液相变过程和空腔外的气体输运过程。

参考文献

[1]孔祥言. 高等渗流力学 [M]. 2版. 合肥: 中国科学技术大学出版社, 2010. (KONGXiang-yan.AdvancedMechanicsofFluidsinPorousMedia[M]. 2nded.Hefei:UniversityofScienceandTechnologyPress, 2010.)

[2]刘伟, 范爱武, 黄晓明. 多孔介质传热质理论与应用 [M]. 北京: 科学出版社, 2006. (LIUWei,FANAi-wu,HUANGXiao-ming.TheoryandApplicationofHeatandMassTransferinPorousMedia[M].Beijing:SciencePress, 2006.

[3]PRUESSK.TOUGH2:Ageneral-purposenumericalsimulatorformultiphasefluidandheatflow[R].LBL-29400,LawrenceBerkeleyNationalLaboratory,UniversityofCalifornia, 1991.

[4]PRUESSK,OLDENBURGCM,MORIDISGJ.TOUGH2user’sguide[R]. 2nded.LBL-43134,LawrenceBerkeleyNationalLaboratory,UniversityofCalifornia, 1998.

[5]WUYS,PRUESSK.Numericalsimulationofnon-isothermalmultiphasetracertransportinheterogeneousfracturedporousmedia[J].AdvancesinWaterResources, 2000, 23(7): 699-723.

[6]CLASSH,HELMIGR,BASTIANP.Numericalsimulationofnon-isothermalmultiphasemulticomponentprocessesinporousmedia: 1.Anefficientsolutiontechnique[J].AdvancesinWaterResources, 2002, 25(5): 533-550.

[7]NITAOJJ.User’smanualfortheUSNTmoduleoftheNUFTcode[R]. 2nded.UCRL-MA-130653,LawrenceLivermoreNationalLaboratory, 1998.

[8]NITAOJJ.ReferencemanualfortheNUFTflowandtransportcode[R]. 2nded.UCRL-MA-130651-REV-1,LawrenceLivermoreNationalLaboratory, 2000.

[9]HELMIGR,BASTIANP,CLASSH,etal.ArchitectureofthemodularprogramsystemMUFTE-UGforsimulatingmultiphaseflowandtransportprocessesinheterogeneousporousmedia[J].MathematischeGeologie, 1998, 2(64): 123-131.

[10]刘昌军. 非饱和水气两相渗流数值模拟研究及应用 [D]. 南京: 河海大学, 2005. (LIUChang-jun.Studyonnumericalsimulationofunsaturatedseepagebasedonwater-gastwo-phaseflowtheoryanditsapplication[D].Nanjing:HehaiUniversity, 2005.)

[11]刘晓丽, 梁冰, 王思敬, 等. 水气二相渗流与双重介质变形的流固耦合数学模型 [J]. 水利学报, 2005, 36(4): 405-412. (LIUXiao-li,LIANGBing,WANGSi-jing,etal.Fluid-solidcoupledmathematicalmodelforwater-airtwo-phaseinfiltrationanddeformationofdualporousmedia[J].JournalofHydraulicEngineering, 2005, 36(4): 405-412.)

[12]黄朝琴, 姚军, 王月英, 等. 裂隙介质两相渗流数值模拟研究 [J]. 中国科学: 技术科学, 2011, 41(9): 1 240-1 248. (HUANGZhao-qin,YAOJun,WANGYue-ying,etal.Numericalstudyontwo-phaseflowthroughfracturedporousmedia[J].SciChinaTechSci, 2011, 41(9): 1 240-1 248.)

[13]FALTAR,PRUESSK,JAVANDELI,etal.Numericalmodelingofsteaminjectionfortheremovalofnonaqueousphaseliquidsfromthesubsurface: 1.Numericalformulation[J].WaterResourcesResearch, 1992, 28(2): 433-449.

[14]JAMBHEKARVA.Forchheimerporous-mediaflowmodels:Numericalinvestigationandcomparisonwithexperimentaldata[D].Stuttgart:UniversitätStuttgart, 2011.

[15]ZENGZW,GRIGGR.Acriterionfornon-Darcyflowinporousmedia[J].TransportinPorousMedia, 2006, 63(1): 57-69.

[16]王铁良, 曹渊, 张建鑫. 地下爆炸空腔压力和温度历程数值模拟 [J]. 计算物理, 2011, 28(5): 713-718. (WANGTie-liang,CAOYuan,ZHANGJian-xin.Numericalsimulationofcavitypressureandtemperatureinundergrounddetonation[J].ChineseJournalofComputationalPhysics, 2011, 28(5): 713-718.)

[17]杨世铭, 陶文铨. 传热学 [M]. 3版. 北京: 高等教育出版社, 1998. (YANGShi-ming,TAOWen-quan.HeatTransfer[M]. 3rded.Beijing:HigherEducationPress, 1998.)

[18]WAGNERW,PRUSSA.TheIAPWSformulation1995forthethermodynamicpropertiesofordinarywatersubstanceforgeneralandscientificuse[J].JPhysChemRefData, 2002, 31(2): 387-535.

[19]王洪涛. 多孔介质污染物迁移动力学 [M]. 北京: 高等教育出版社, 2008. (WANGHong-tao.DynamicsofFluidFlowandContaminantTransportinPorousMedia[M].Beijing:HigherEducationPress, 2008.)

[20]REIDRC,POLINGBE,PRAUSNITZJM.ThePropertiesofGasesandLiquids[M]. 4thed.NewYork:McGrawHill, 1987.

[21]MILLINGTONRC,QUIRKJP.Permeabilityofporoussolids[J].TransactionsoftheFaradaySociety, 1961, 57: 1 200-1 207.

[22]CHUEHC,BANGERTHW,DJILALIN.Integratedadaptivenumericalmethodsfortransienttwo-phaseflowinheterogeneousporousmedia[C]// 7thInternationalConferenceonComputationalFluidDynamics,Hawaii, 2012.

[23]LEVERETTMC.Capillarybehaviorinporoussolids[J].TransAIME, 1941, 142(1): 152-169.

[24]王铁良, 张建鑫, 曹渊. 地下爆炸气体输运的一种双孔隙度数学模型 [J]. 应用力学学报, 2011, 28(6): 565-569. (WANGTie-liang,ZHANGJian-xin,CAOYuan.Adualporositymathematicalmodelofgastransportationonundergrounddetonation[J].ChineseJournalofAppliedMechanics, 2011, 28(6): 565-569.)

[25]王铁良, 曹渊, 邝飞虹, 等. 气体在包含空洞的岩体中渗透的数学模型简化 [J]. 现代应用物理, 2014, 5(1): 45-50. (WANGTie-liang,CAOYuan,KUANGFei-hong,etal.Simplifiedmathematicalmodelforgaspermeatingthroughhollowrockmass[J].ModernAppliedPhysics, 2014, 5(1): 45-50.)

收稿日期：2016-01-20；修回日期：2016-03-04

作者简介：何增(1991- )，男，陕西西安人，研究实习员，硕士研究生，主要从事计算流体力学研究。 E-mail:hezeng@nint.ac.cn

中图分类号：O35

文献标志码：A

文章编号：2095-6223(2016)021001(9)

Mathematical Model of Non-Isothermal Liquid-Gas Two-Phase Multi-Component Seepage Flow in Porous Media

HE Zeng,TIAN Zhou,WANG Tie-liang

(Northwest Institute of Nuclear Technology,Xi’an710024,China)

Abstract:A set of mathematical model is developed for non-isothermal two-phase multi-component seepage flow by analyzing the interactions of gas and liquid in porous media. Special processes are considered in high temperature and high pressure environment, such as non-Darcy flow, water transition and heat radiation, the convection, dispersion, source, and sink terms. Moreover, a complete set of constitutive relations is proposed to close the governing equations, among which the formulas for calculating the specific internal energy and the specific enthalpy are derived. Finally, this model is used to simulate the migration of explosive gas after underground detonation. The result suggests that, compared with the gas phase seepage model, this model can provide a more reasonable description for the gas transport in geological medium.

Key words:two-phase seepage flow；non-isothermal flow；mathematical model；constitutive relations；gas transport