T形钢管混凝土短柱轴压试验
陈 雨, 沈祖炎,2, 雷 敏, 李元齐,2
(1.同济大学 土木工程学院,上海 200092;2.同济大学 土木工程国家防灾减灾重点实验室,上海 200092;3.西南交通大学 土木工程学院,四川 成都 610031)
T形钢管混凝土短柱轴压试验
陈雨1, 沈祖炎1,2, 雷敏3, 李元齐1,2
(1.同济大学 土木工程学院,上海 200092;2.同济大学 土木工程国家防灾减灾重点实验室,上海 200092;3.西南交通大学 土木工程学院,四川 成都 610031)
摘要:进行了6根普通构造T形钢管混凝土轴压短柱的试验研究,以考察无加劲措施T形钢管混凝土柱的变形特征、破坏模式和承载能力.试验的主要参数有管壁宽厚比、截面高宽比.试验结果表明,由于 T形钢管混凝土柱的核心混凝土延缓了钢管的局部屈曲,尽管该组合构件承载力不能得到有效提高,但延性却得到相当改善;阳角钢管对混凝土提供了较强的约束,而由于钢板与混凝土的分离,阴角钢管几乎不能约束混凝土;T形钢管混凝土柱的破坏形态主要为钢管鼓曲及此部位及阴角区域混凝土压碎破坏;管壁宽厚比越小, 初始鼓曲发生越晚, 钢管对混凝土的约束效应越强,承载力越高、延性越好.最后采用现有规范或规程的计算公式对试件轴压承载力进行了计算,并对不同计算方法的适用性进行了探讨.
关键词:T形钢管混凝土; 轴压; 短柱; 宽厚比; 局部屈曲; 承载力
钢管混凝土结构拥有承载能力高、抗震抗性能优越、施工方便、耐火性能好等优点,目前已广泛应用于工程建设的各个领域.钢筋混凝土异形柱结构拥有满足室内空间美学要求、可持续化、人性化的优点,目前我国在许多省市已建造了大量钢筋混凝土异形柱结构多层住宅.异形钢管混凝土柱结合了这2个结构的优点,在未来的小高层建筑中有着广阔的应用前景.近年来国内研究者对异形钢管混凝土柱力学性能的研究予以了广泛的关注,主要侧重于轴压短柱、偏压短柱的静力性能研究、构件的抗震性能研究以及采用不同的加劲措施来改善异形钢管混凝土柱的延性和承载力[1-15].随着钢结构构件生产加工工艺的不断提高与完善,异形钢管有望通过生产流水线的改进一次加工成型,方便施工,减小异形钢管因为焊接和弯折加工产生的生产成本,从而有利于促进该类结构体系在工程中的应用.而该类T形钢管混凝土柱的轴压性能尚未得到深入了解,为此本文进行了6根普通T形钢管混凝土短柱的轴压试验,考察该类截面构造T形钢管混凝土柱的变形特征、破坏模式、承载能力和延性等,分析了钢管宽厚比、截面长宽比等对构件受力性能的影响.
1试验概况
T形截面翼缘宽度与腹板高度比例的变化使T形截面自身变化复杂.本文主要研究T形截面翼缘宽度B与腹板方向总高度H相同的T形钢管混凝土柱,截面形式见图1.图1中hf和hw分别为柱翼缘高和柱腹板高;bw和b1分别为柱腹板宽和柱翼缘外伸长度.为了避免试件过短而受端部效应影响及过长而受弯曲效应影响,试件长度取截面高度的3倍.为考察管壁不同宽厚比对该类柱轴心受压力学性能的影响,钢管管壁宽厚比取:31.2,35.7,37.5,41.6,50.0和60.0.试件的几何及材料属性相关细节见表1,其中,t和L分别为钢管壁厚和柱高;fy为钢材屈服强度;εb为钢管初始鼓曲时的名义纵向应变;εu为峰值荷载名义应变;N0为试件的名义荷载,N0=fyAs+fcAc,Ac和As分别为混凝土和钢管的
截面面积;Nb和Nue分别为钢板初始鼓曲时试件的荷载、峰值荷载,Nb列的A,B分别代表峰值荷载后与峰值荷载前;ξ为混凝土约束效应系数,ξ=(fyAs)/(fcAc),fc为混凝土轴心抗压强度;α为混凝土提高系数,α=(Nue-N0)/(fcAc);DI为延性指数.表1中所有试件的混凝土立方体抗压强度(fcu)都为38.22 Mpa,所有试件的hf,bw都为100 mm.钢管采用Q235碳素钢,柱身由2片弯折板和1片直板开剖口熔透焊接而成.钢管的上下端分别焊接2块相互平行的端板.为防止试验时构件端部发生局部压屈,在试件的上下端分别围绕柱身焊接厚20 mm、高40 mm的环箍.为了便于混凝土的浇筑,试件的上端板开一外缘尺寸比钢管柱内缘尺寸每侧小15 mm的T形孔.试件采用搅拌机现场搅拌混凝土,一次性浇筑完成,所有试件的混凝土经振捣密实后均高于构件上端板5~10 mm.试验前用砂轮磨光机将高出上端板板面的混凝土磨平至与上端板平齐.

图1 试件截面形式

表1 试件参数及试验结果
试验在1 000 t多功能试验机上进行,整个加载装置由竖向加载系统和水平支撑装置组成,见图2.1 000 t竖向作动器通过竖直销栓装置与轴压试件端板连接.水平支撑装置保证试件在竖直平面内垂直移动,并限制试件发生侧向位移,以保证短柱上端铰支.短柱的下端由螺栓将底板固定在底座上.加载时采用位移加载,钢管屈服前每分钟竖向位移为0.5 mm,钢管屈服后每分钟竖向位移为1.0 mm,直至试件破坏或观测认为不宜继续加载为止.
为了准确测量柱的轴向变形,在柱的角部布置了6个纵向位移计.位移计的平面位置根据合力矩原理,使各位移计的力矩中心位于试件的形心处,从而位移计读数的平均值反映试件的纵向位移.在试件柱高的中部截面每隔一定距离各贴1对纵向应变片和横向应变片,以监测钢管的应变发展情况、截面受力是否均匀和不同部位钢管对混凝土约束效应的强弱.测点的布置见图3.截面翼缘宽度为250 mm的试件无15,16,19,20号应变片.
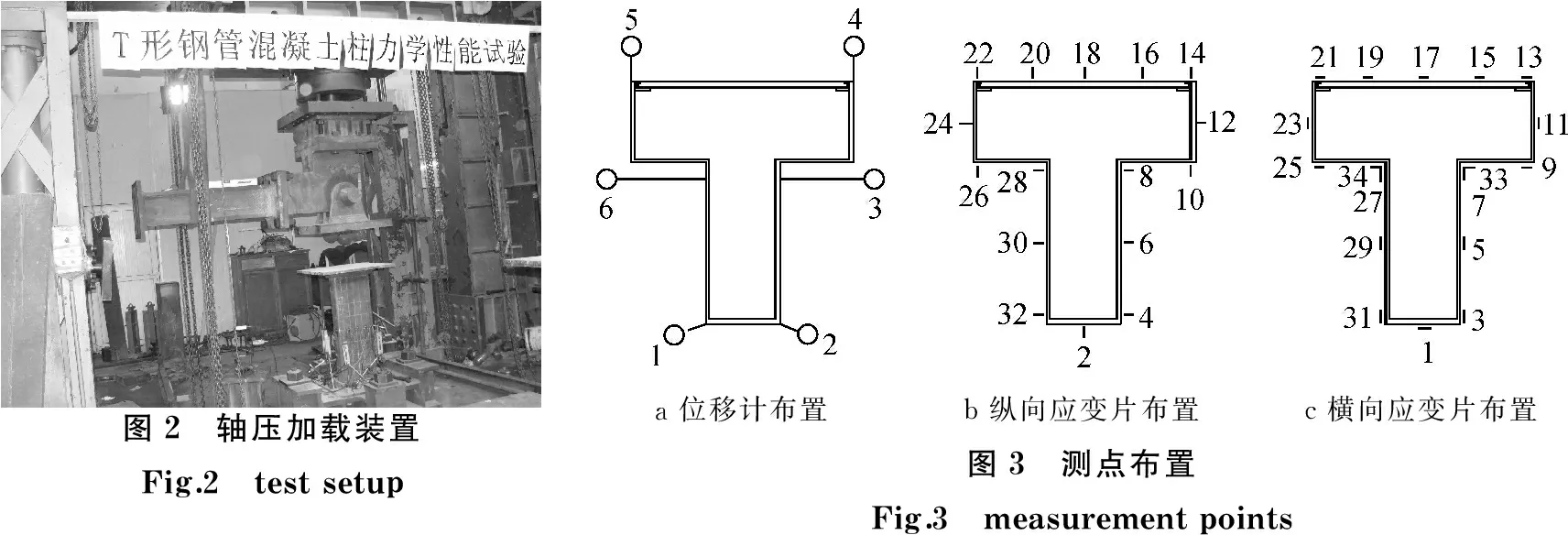
图2 轴压加载装置Fig.2 testsetupa位移计布置b纵向应变片布置c横向应变片布置图3 测点布置Fig.3 measurementpoints
2试验结果分析与讨论
2.1试验破坏模式及现象分析
通过试验可以发现如下规律性的破坏现象:
(1)T形钢管混凝土短柱压溃时的破坏模式主要为钢管受压鼓曲破坏,同时该部位及阴角部位的混凝土压碎破坏;随着轴向位移率的增加,钢管在试件的高度上形成2个或3个鼓曲波;试件破坏时柱身整体呈腰鼓状,即面6和面7的交线、面3和面4的交线从垂直于面7和面3的方向看去呈腰鼓状,但面5和面6的交线及面5和面4的交线从垂直于面5的方向看去变化不明显.这说明阴角周边附近的阳角受阴角区域的影响,其钢管对混凝土的约束作用小于翼缘直边(面5)所在的阳角.
(2)试件的鼓曲波首先出现在柱身的宽面5,鼓曲波的首次出现主要受管壁宽厚比的影响,宽厚比越大,鼓曲波出现越早.随着宽厚比的减小,鼓曲波的出现有在峰值荷载前、峰值荷载左右、峰值荷载后改变的规律,即:T300-5的B/t=60.00,当荷载上升到峰值荷载的89.2%时,面5在柱高45~65 cm区域中部出现轻微鼓曲;T300-6A的B/t=50.00,当荷载上升至峰值荷载的99.2%时,面5在柱高25~35 cm的区域出现微鼓;T300-6B的B/t=50.00,当荷载上升到峰值荷载的99.7%时,面5在柱高75~85 cm区域出现轻微鼓曲; T250-6的B/t=41.71,当荷载下降到峰值荷载的96.3%时,面5在柱高60 cm附近出现轻微鼓曲;T300-8的B/t=37.50,当荷载下降到峰值荷载的92.5%时,面5在柱高75~85 cm区域出现轻微鼓曲;T250-8的B/t=31.25,当荷载下降到峰值荷载的86.5%时,面5在柱高50 cm附近出现微鼓.
(3)即使首次鼓曲波出现在峰值荷载前,试件承载力也有较大的增加趋势;试件在整个破坏过程表现出较好的延性.
(4)在峰值荷载后,随着轴向位移的增加, 其他各面也相继鼓曲,尤其是阴角部位处的面2和面8较其他面率先出现鼓曲(但其出现鼓曲晚于面5),面5、面2、面8出现连续鼓曲波.
(5)在峰值荷载后,阴角区域的两面交线(面2与面3的交线、面7与面8的交线)在柱高中部附近出现明显向外鼓凸的现象.当试件T300-6的试验完成后,在其他试件的阴角竖直线上距柱高中部上下各10 cm处布置了沿阴角角平分上的水平向位移计,水平位移计的位移监测结果说明,从加载一开始阴角线即出现向外的鼓凸变形.这说明阴角区域的钢板和混凝土有分离的现象,阴角区域的钢板不对混凝土产生约束作用.
(6)在试件钢管出现鼓曲波的部位以及试件的阴角部位核心混凝土已严重压碎,而在未出现鼓曲波的部位核心混凝土的破坏不很明显.试件的典型破坏形态如图4所示.
2.2试验结果分析
2.2.1轴力-纵向名义应变关系
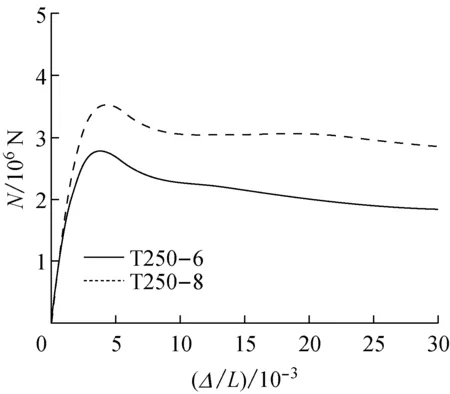
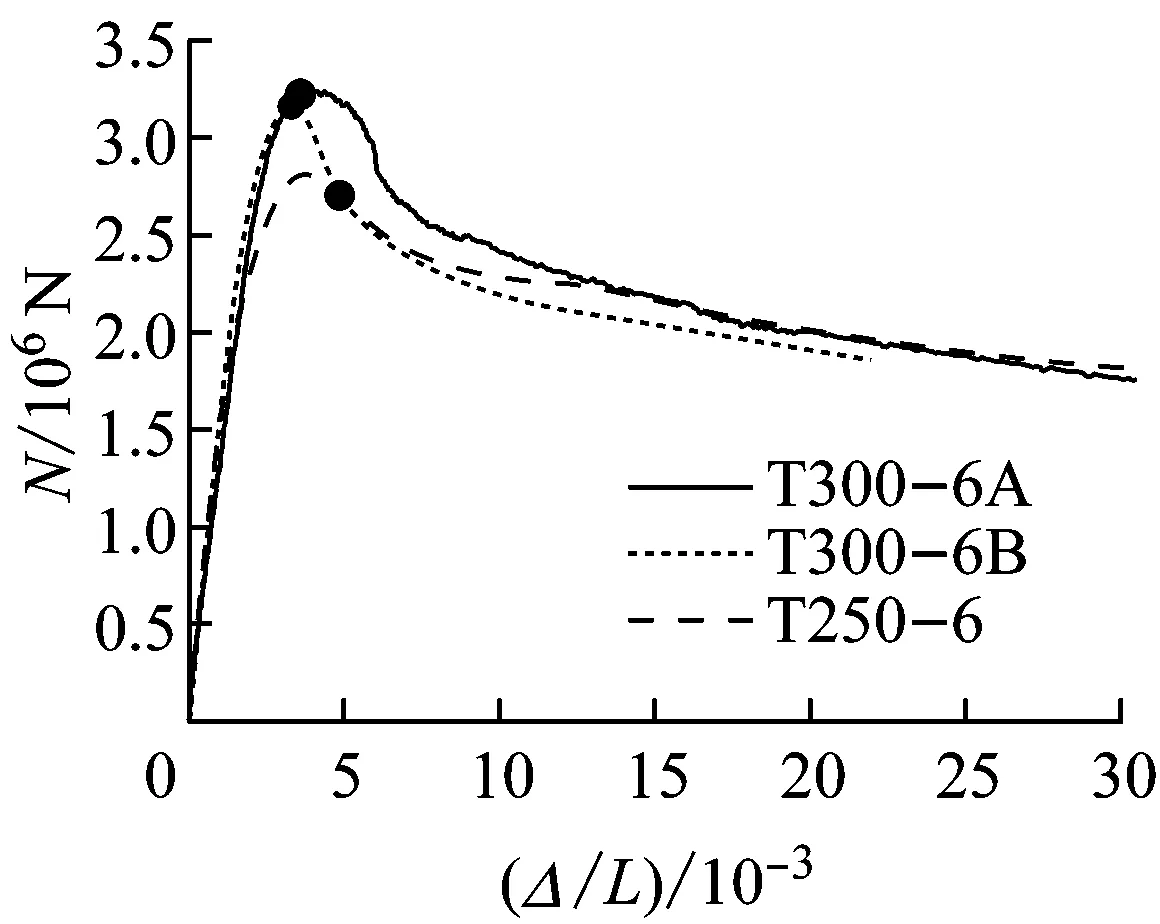
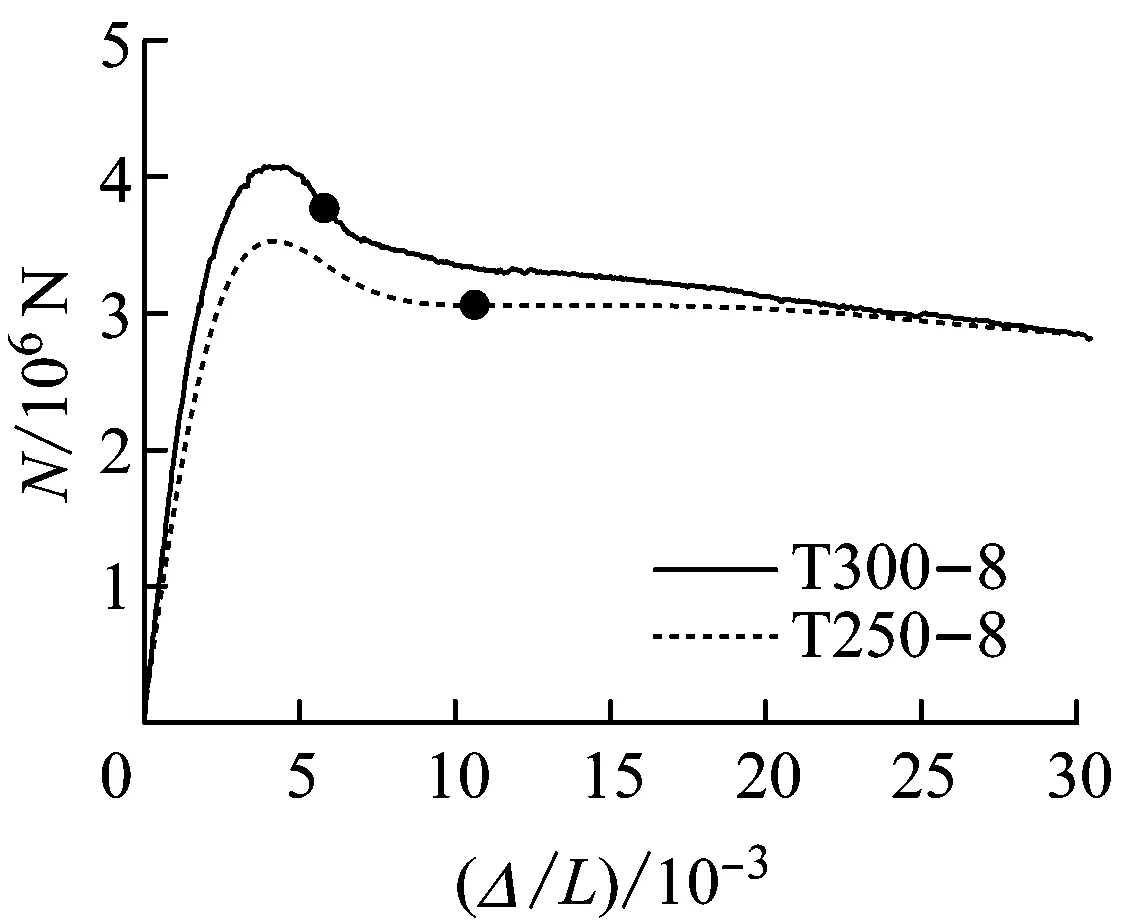
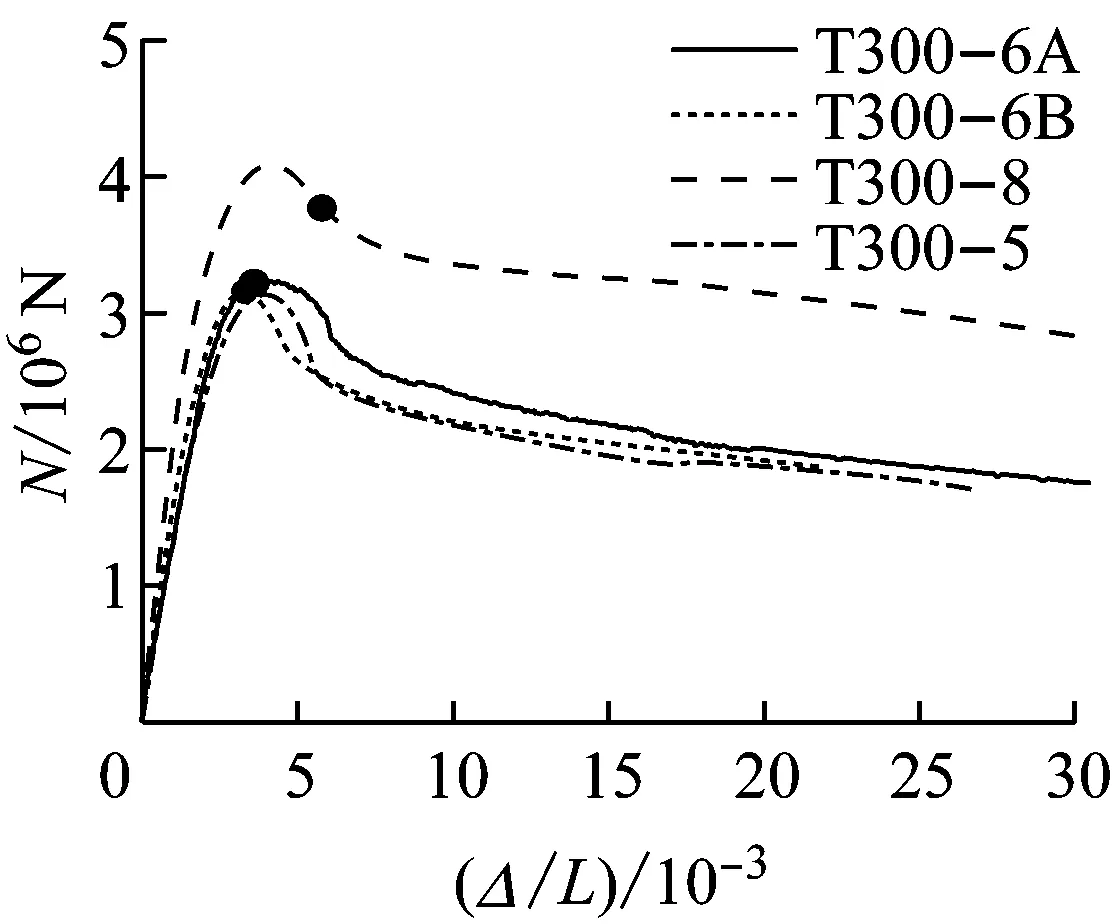
从图5可以看出,T形钢管混凝土短柱的轴向荷载-纵向名义应变(纵向名义应变为竖向平均位移除以柱高)曲线基本都呈直线上升、曲线偏转上升与下降、平缓下降的特征,反映规律如下:
(1)荷载达到峰值荷载的70%~80%前,荷载-纵向名义应变曲线基本呈直线.此阶段构件处于弹性受荷状态,钢管与混凝土一般各自独立承担外荷载.
(2)随着外荷载的增加,纵向变形加速增长,荷载纵向名义应变曲线出现偏转,直到达到峰值荷载后出现曲线下降.此期间由于T形钢管混凝土柱截面钢管宽厚比的不同,宽面钢管首先出现向外微鼓的荷载时刻有所差异:宽厚比大于等于50的试件,在峰值荷载前宽面5均出现了向外微鼓,但外荷载仍可继续增加;宽厚比小于50的试件,宽面的首次微鼓出现在峰值荷载后.

a整体腰鼓b面5鼓曲c阴角外鼓

d面5钢管鼓曲e阴角部位压碎

a T300系列
b T250系列
(3)在峰值荷载后,随着纵向位移的继续增加,钢管各面陆续出现鼓曲,曲线出现下降.此后都有一个较长的平缓段,而且宽厚比越小,下降段越平缓,显示了T形钢管混凝土短柱具有一定的延性.
(4)从表1可以看出,在管壁厚度、钢材强度相同的情况下,管壁宽厚比越大(对应含钢率越小),构件达到极限承载力时对应的峰值应变就越小:T300-6A和T300-6B的峰值应变小于T250-6试件,且T300-8试件的峰值应变小于T250-8试件.从T300-6A,T300-6B,T300-5,T300-8试件的峰值应变对比可以看出,尽管T300-5试件的管壁厚度小于T300-6A和T300-6B试件,但其峰值应变却与T300-6A试件的峰值应变相近,因此试件的峰值应变还受钢材屈服强度的影响.从而T形钢管混凝土柱达到极限承载力时的峰值应变可归结为约束效应系数影响.约束效应系数越大,峰值应变就越高.
图6给出了不同参数影响下的荷载-纵向名义应变曲线,图中圆点所示为各试件管壁发生初始局部鼓曲时对应的轴力-纵向名义应变点.从图6a和6b可以看出,截面宽厚比越小,初始鼓曲的应变值就越大.从图6c可以看出,初始鼓曲的应变值与钢材屈服强度没有关系,而只与管壁宽厚比有关,管壁宽厚比越小,初始鼓曲出现得越晚.
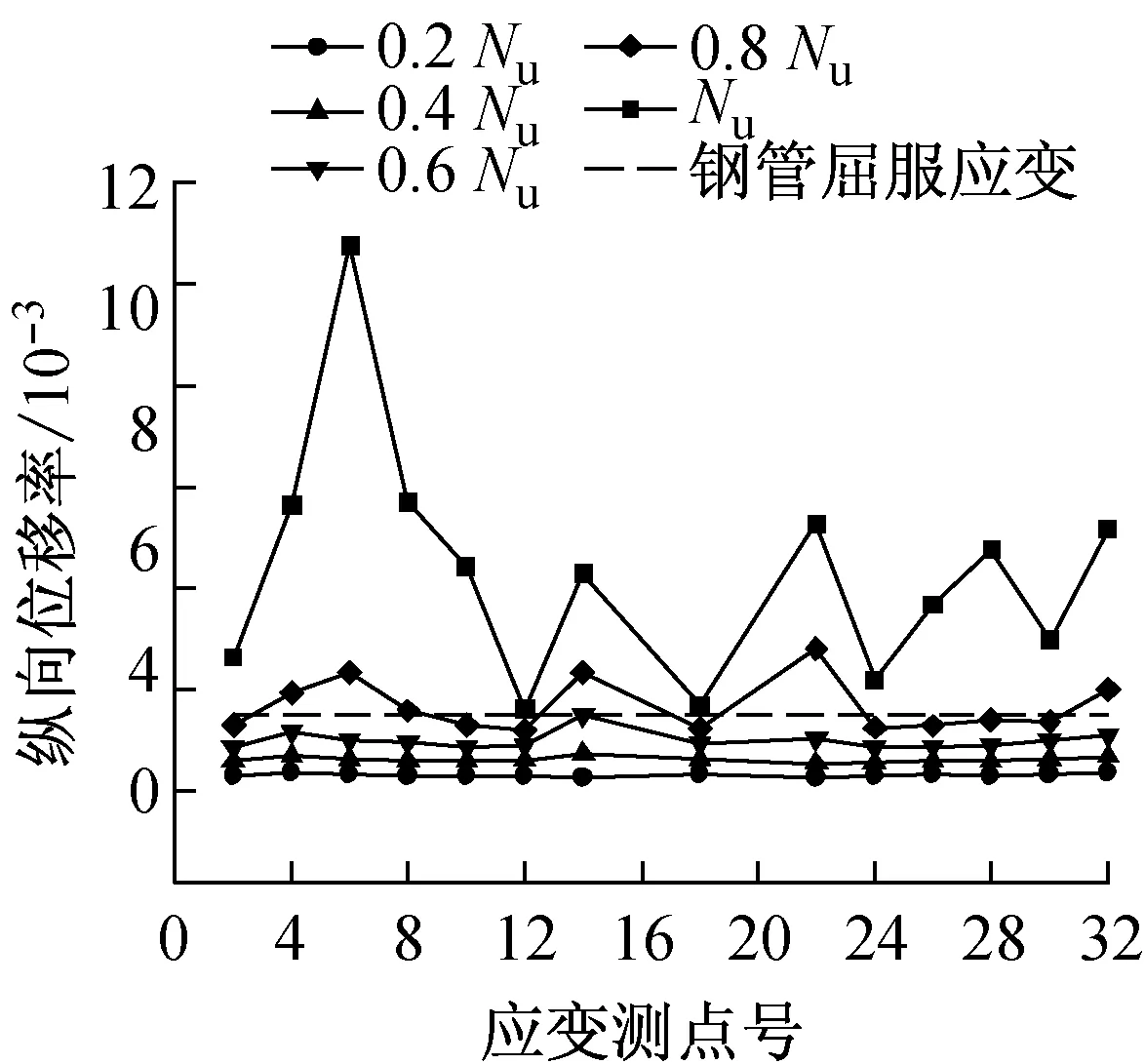
2.2.2荷载-纵向应变关系
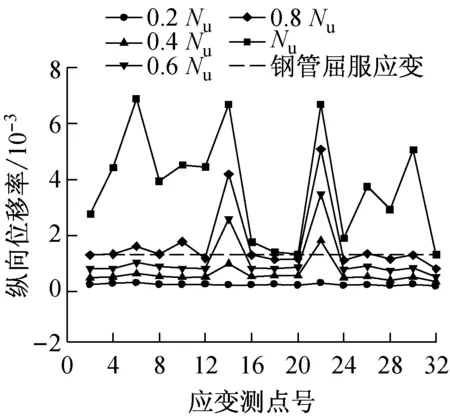
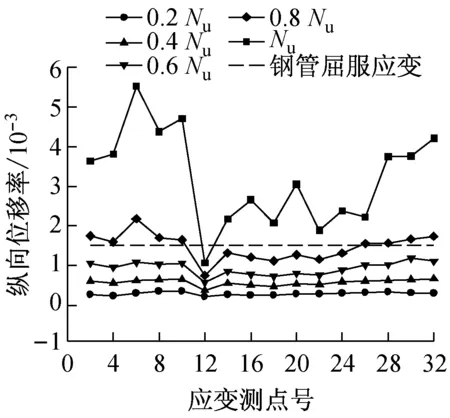
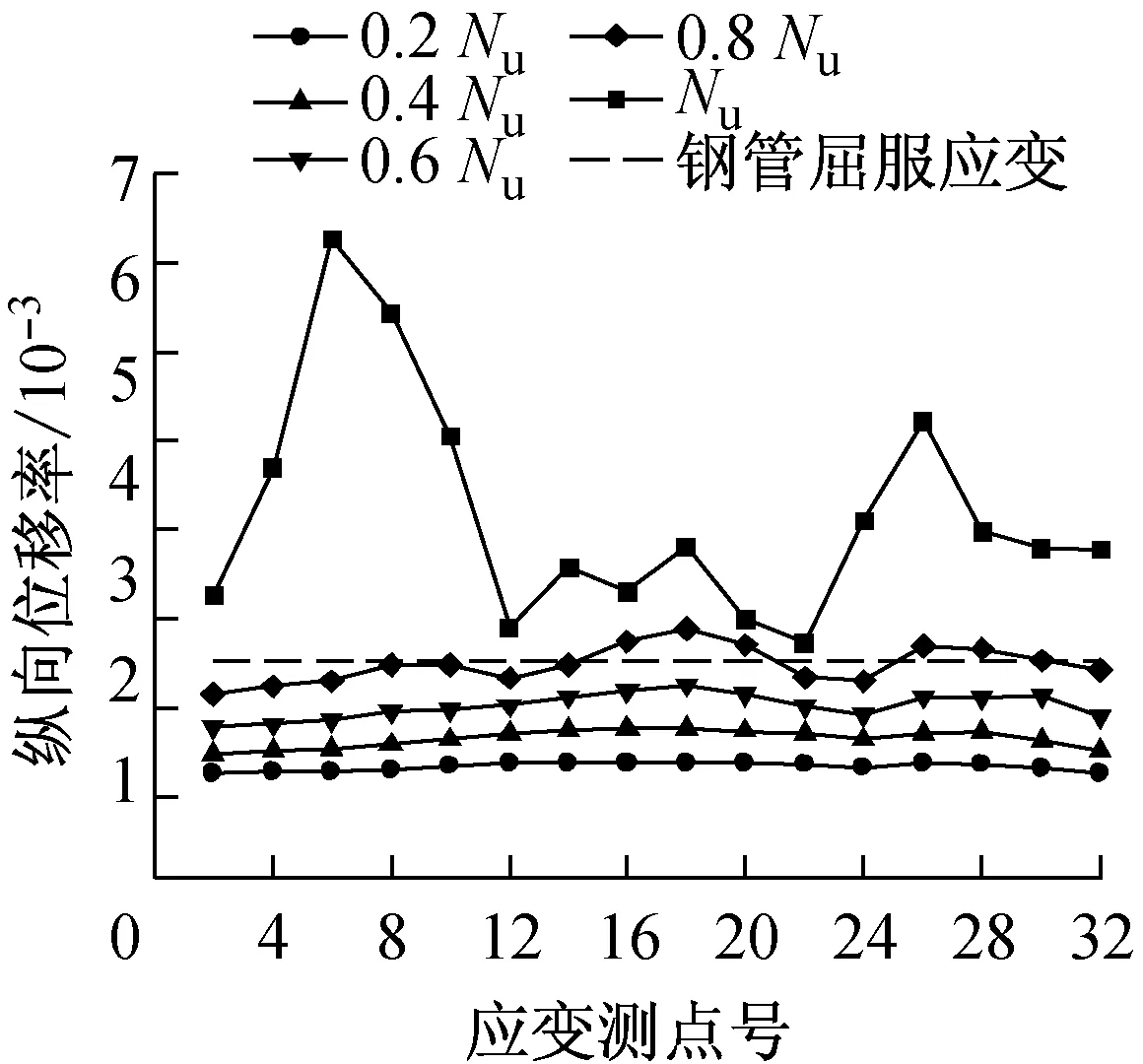
图7给出了0.2,0.4,0.6,0.8和1.0倍极限承载力(Nu)时各测点的纵向应变,测点布置如图3所示.由图7可知:当荷载达到峰值荷载的80%前,整个截面的应变分布在各荷载阶段是比较均匀的;而且在达到0.6Nu时,各荷载阶段之间的应变差基本接近,说明此期间构件处于弹性阶段.荷载达到0.8Nu时,0.6Nu~0.8Nu之间的应变差已大于0~0.2Nu,0.2Nu~0.4Nu,0.4Nu~0.6Nu各阶段的应变差,这说明此区间构件已开始向弹塑性发展.荷载超过0.8Nu后,应变随着外荷载的增加而明显迅速增加,达峰值荷载时,钢管全截面的应变分布已完全不均匀,相当多的测点应变远大于钢管的屈服应变,这是由于这些点处于管壁鼓曲处,试验结束时该部位呈现鼓曲状.同时说明,对于屈服强度小于305 MPa的钢材与混凝土立方体抗压强度大于等于38.2 MPa的混凝土组成的T形钢管混凝土柱,能够保证在试件达到承载力前钢管截面出现全截面屈服.
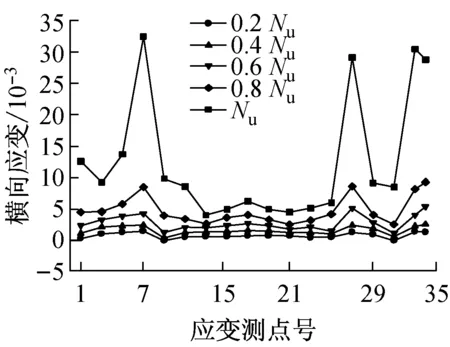
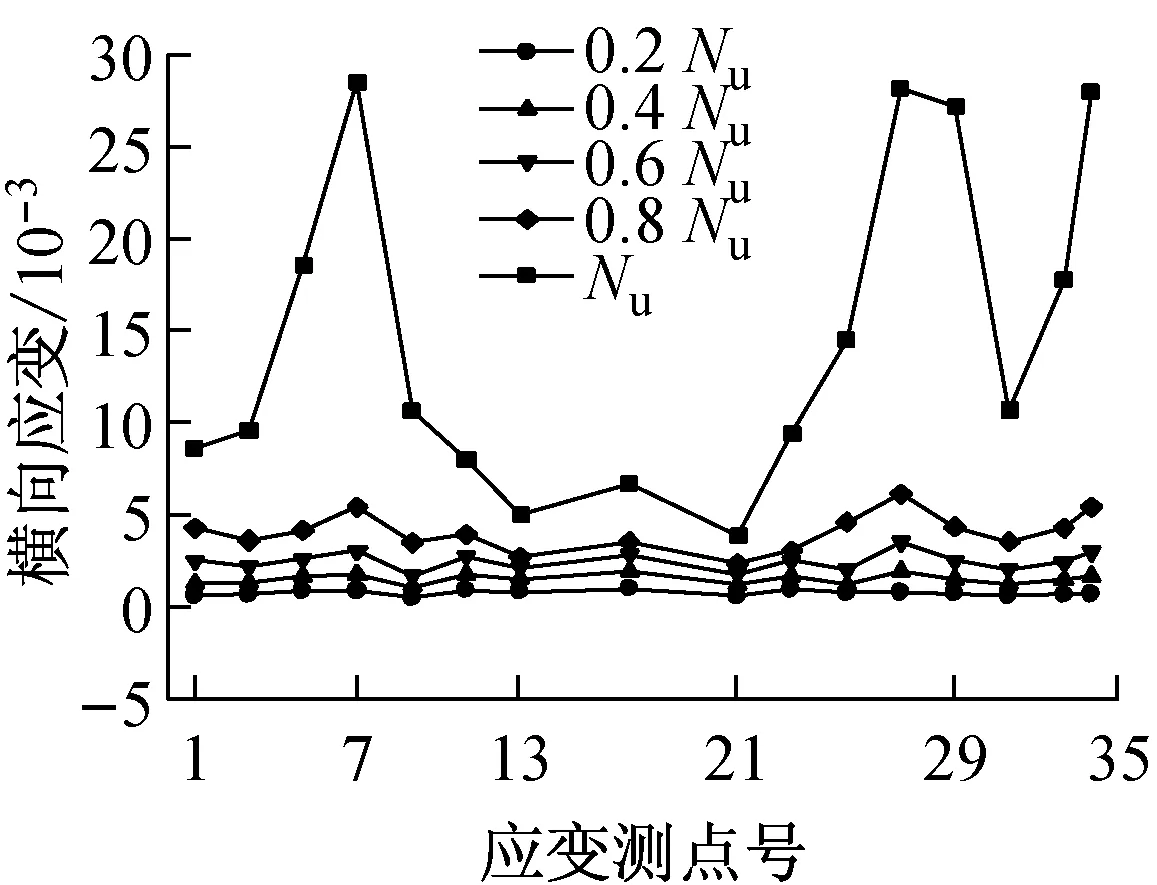
2.2.3荷载-横向应变关系
a 管壁厚6 mm
b 管壁厚8 mm
c 不同管壁厚及钢材屈服强度
a T300-6A

b T300-6B
c T300-8
d T300-5

e T250-6
f T250-8
图8给出了0.2,0.4,0.6,0.8和1.0倍极限承载力时各测点的横向应变分布.从图8可看出,在荷载达到0.6Nu前,截面上的应变分布比较均匀,而且应变数值相对较小,这说明钢管和混凝土各自单独工作承担外荷载.之后,由于混凝土进入塑性,发生塑性流动,泊松比变大,体积膨胀,挤压钢管壁,导致钢管壁的横向应变增加.与此对应,钢管约束混凝土的膨胀变形对混凝土产生套箍效应.同时,由于截面的不规则性,横向应变存在较大的不均匀性.值得指出的是,对于所有的试件,其阴角处的横向应变(应变片7,27,33,34)远大于其他部位,其原因在于阴角处两板件的相互支撑作用不强,轴向荷载作用下阴角处存在较大的外鼓变形,因而对于T形钢管混凝土柱,其阴角部位是一约束作用相对较小的弱约束区或对混凝土的无约束区.另外,板件中部的应变大于板件角部的应变(应变片5的应变大于应变片3的应变,应变片29的应变大于应变片31的应变),在面5上,板件中部的应变大于角部的应变这一规律对于所有试件似乎不是很明显,但对于钢管混凝土柱T300-8,T300-5,T250-6这3个试件这一规律得到了明显的验证,应变值从17号应变片向左右两侧的15,13, 19和21号应变片逐渐减小,其主要原因在于,角部板件受到相邻板件的支约束,其刚度大于中央板件,因此板件中部由于存在鼓曲变形或者有鼓曲的趋势而使得其横向应变大于角部的横向应变,从而板件中部相对于板件角部而言,对混凝土的约束作用相对较弱.

a T300-A

b T300-6B
c T300-8

d T300-5
e T250-6

f T250-8
2.2.4试件延性分析
延性反映了结构和构件吸收能量的能力,表1给出了所有试件的延性指数.基于荷载和竖向位移的延性指数定义为
(1)
式中:Δu为荷载下降到峰值荷载85%时的轴向位移;Δy为荷载位移曲线对应屈服点的位移,由等能量法确定(图9),即:OA为荷载位移曲线过原点的切线,直线AC使阴影部分OAB的面积等于阴影部分BCB的面积.图9中Δ为位移,Δp为峰值荷载时的轴向位移;P为施加的荷载;Py为屈服时的荷载;Pmax为峰值荷载.从表1和图5可看出T形钢管混凝土短柱在轴压下具有较好的延性.柱的延性受宽厚比影响较大,从截面宽度为300 mm的柱的延性值可看出,钢管宽厚比越小,钢材强度越高,则约束效应越强,构件的延性越好;从不同翼缘宽度的钢管混凝土柱(T300-8,T250-8)的延性可以看出,随着管壁宽厚比的减小,约束效应增大,柱的延性总体上呈增大的趋势.
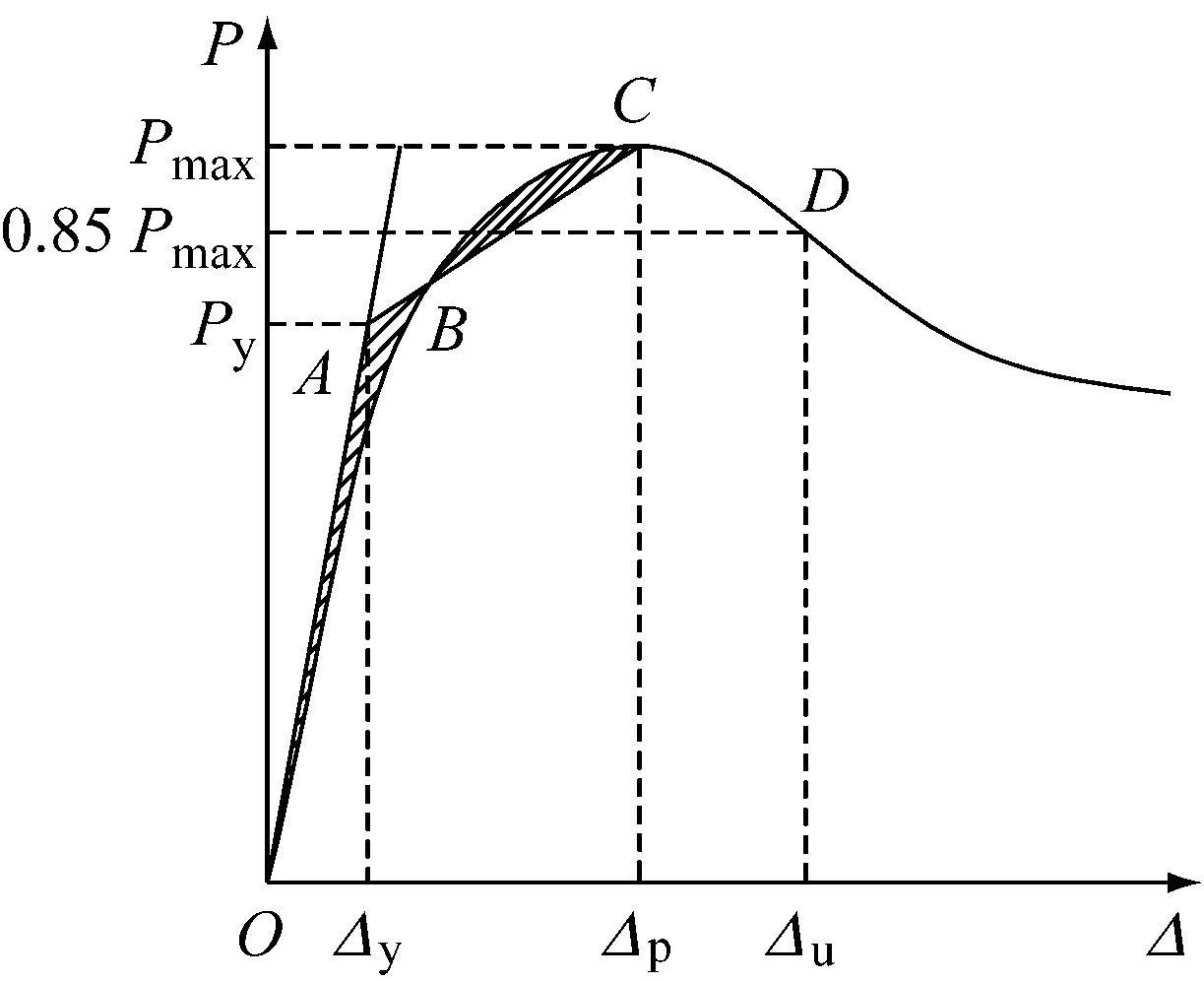
图9 延性指数的确定
3不同规范计算比较
国内外目前关于钢管混凝土的设计规范或规程主要针对圆形、方形、矩形钢管混凝土,尚无有关异形钢管混凝土柱的设计条文.本文暂用具有代表性的美国ACI、欧洲EC4、日本AIJ、我国的《矩形钢管混凝土结构技术规程》(CECS159—2004)来评价其对T形钢管混凝土短柱的轴压承载力的适用性,上述规范公式相应为:
Nu-ACI=0.85[0.85fcAc+fyAs]
(2)
(3)
Nu-AIJ=0.85Acfc+AsF
(4)
(5)
(6)
式中:γc和γs为系数;f和fu分别为钢材的设计强度和抗拉强度.
表2和表3给出了各规程计算值与试件承载力试验值的比值的计算结果.从表2可见,ACI和AIJ认为试件达到极限承载力时,截面上混凝土的应力为0.85fc,较低地估计了该类柱混凝土的峰值强度,ACI 还考虑了荷载初偏心的影响,乘以0.85的折减系数,从而二者都较为保守估计了T形钢管混凝土试件的承载力;而EC4和CECS159较好地估算了试件的承载力.
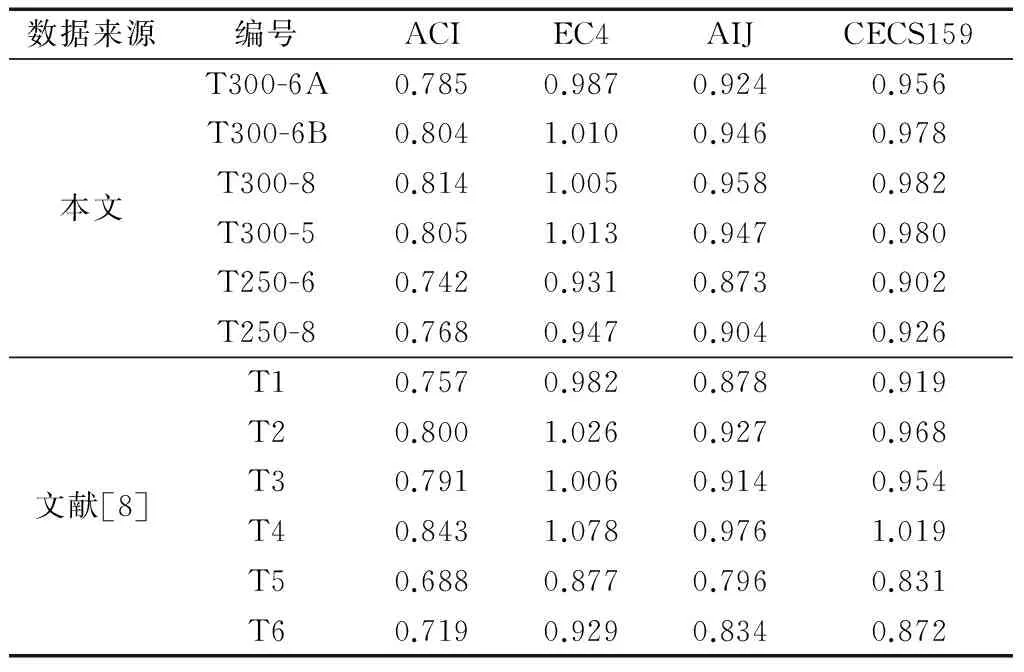
表2 不同规程计算值与试验值的比值

表3 不同规程计算数据的平均值与标准差
4结论
根据6根T形钢管混凝土短柱的试验过程、试件的破坏形态、试验结果分析可以得到以下结论:
(1)T形钢管混凝土轴压短柱压溃时的破坏属于鼓曲破坏以及该部和阴角区域混凝土压碎破坏.板面鼓曲首先出现在钢管板面的宽面,之后其他各面也相继鼓曲,试验结束时沿柱高形成连续鼓曲波.首次鼓曲的时间随板面宽厚比的减小而延后,管壁宽厚比大于等于50的试件,首次鼓曲均出现在峰值荷载前,而宽厚比小于50的试件,首次鼓曲出现在峰值荷载后.
(2)从荷载-纵向名义应变曲线可以看出:在荷载达峰值荷载的70%~80%前,荷载-纵向名义应变曲线呈直线,构件处于弹性阶段受荷.之后曲线偏转,试件进入弹塑性状态;在峰值荷载后,经历了下降段,曲线有较长的平缓段,显示T形钢管混凝土短柱有一定的延性.约束效应系数越高,延性越好,同时,约束效应系数越大,达到峰值荷载时的应变也越大.
(3)从试件在不同阶段的纵向应变分布图可见,在0.8Nu前,试件截面应变发展均匀;在0.8Nu后,纵向应变分布逐渐不均匀,在峰值荷载时,钢管截面相当多的测点应变远大于钢材屈服应变.
(4)从试件在不同阶段的横向应变分布图可以看出,荷载在0.6Nu前,横向应变较小且基本均匀,钢管与混凝土独立工作;之后,横向应变逐渐增大且不均匀,钢管对混凝土产生约束,混凝土对钢板起侧向支撑作用,阻止钢管板面的向内鼓曲变形,钢管和混凝土产生相互作用,共同承担外荷载.试件截面的阴角及宽厚比较大的板面中部是非约束区或弱约束区,板面阳角部位为强约束区.
(5)约束效应系数越大,混凝土强度提高系数越大.
参考文献:
[1]Chen Z Y, Shen Z Y. Behavior of L-shaped concrete-filled steel stub columns under axial loading: Experiment [J]. Advanced Steel Construction, 2010, 6(2): 688.
[2]林震宇. L形钢管混凝土构件力学性能若干关键问题研究[D]. 上海:同济大学,2009.
LIN Zhenyu. Study on some key problem on behavior of L-shaped concrete-filled steel tubular columns [D]. Shanghai: Tongji University, 2009.
[3]左志亮,蔡健,钱泉,等. 带约束拉杆T形钢管混凝土短柱轴压性能的试验研究[J].土木工程学报, 2011, 44(11): 43.
ZUO Zhiliang, CAI Jian, QIAN Quan,etal. Experimental study on T-shaped CFT stub columns with binding bars subjected to axial compression [J]. China Civil Engineering Journal, 2011, 44(11):43.
[4]左志亮, 蔡健, 刘明峰,等. 带约束拉杆T形钢管混凝土短柱偏压试验研究[J]. 建筑结构学报, 2011, 32(8): 79.
ZUO Zhiliang, CAI Jian, LIU Mingfeng,etal. Experimental study of T-shaped CFT stub columns with binding bars subjected to eccentric load [J]. Journal of Building Structures, 2011, 32(8): 79.
[5]Zuo Z L, Cai J, Yang C. Axial load behavior of L-shaped CFT stub columns with bind bars [J]. Engineering Structures, 2012, 37(5): 88.
[6]Zuo Zhiliang, Cai Jian, Yang Chun,etal. Eccentric load behavior of L-shaped CFT stub columns with binding bars[J]. Journal of Constructional Steel Research, 2012,72(5):105.
[7]杜国锋, 徐礼华, 徐浩然, 等. 钢管混凝土组合T形短柱轴压力学性能研究[J]. 西安建筑科技大学学报:自然科学版, 2008, 40(4): 549.
DU Guofeng, XU Lihua, XU Haoran,etal. Study on behavior of composite T-shaped concrete filled steel tubular short columns under axial compression [J]. Journal of Xi’an University of Architecture & Technology: Natural Science Edition, 2008, 40(4): 549.
[8]杜国锋, 徐礼华,徐浩然,等. 钢管混凝土T形短柱轴压力学性能试验研究[J]. 华中科技大学学报:城市科学版, 2008, 25(3):188.
DU Guofeng, XU Lihua, XU Haoran,etal. Experiment research on behaviour of T-shaped concrete-filled steel tube stubs [J]. Journal of Huazhong University of Science and Technolog:Urban Science Edition, 2008, 25(3):188.
[9]Yang Y L, Yang H, Zhang S M. Compressive behavior of T-shaped concrete filled steel tubular columns [J]. International Journal of Steel Structures, 2010, 10(4): 419.
[10]赵毅, 静行. T形钢管混凝土短柱轴压性能研究[J].武汉理工大学学报, 2011,33(9): 87.
ZHAO Yi, JING Xing. Experimental study of T-shaped concrete-filled steel tube columns under axial compression loading[J]. Journal of Wuhan University of Technology, 2011, 33 (9):87.
[11]王丹, 吕西林. T形、L形钢管混凝土柱抗震性能试验研究[J]. 建筑结构学报, 2005, 26(4):39.
WANG Dan, LV Xilin. Experimental study on seismic behavior of concrete-filled steel T-section, L-section columns[J]. Journal of Building Structures, 2005, 26(4):39.
[12]Shen Z Y, Lei M, Li Y Q,etal. Experimental study on the seismic behavior of concrete-filled L-shaped steel tube columns [J]. Advances in Structural Engineering, 2013, 16(7):1235.
[13]雷敏. T形钢管混凝土构件力学性能若干关键问题研究[D]. 上海:同济大学,2014.
LEI Min. Study on some key problem on behavior of T-shaped concrete-filled steel tubular columns [D].Shanghai: Tongji University, 2014.
[14]徐礼华,杜国锋,温芳,等. 组合T形截面钢管混凝土柱正截面受压承载力试验研究[J]. 土木工程学报,2009,42(6):14.
XU Lihua, DU Guofeng, WEN Fang,etal. Experimental study on normal section compression bearing capacity of composite T-shaped concrete-filled steel tubular columns [J]. China Civil Engineering Journal, 2009,42(6):14.
[15]屠永清, 刘林林,叶英华. 多室式钢管混凝土T形中长柱轴压性能研究[J]. 土木工程学报,2012,45(9):27.
TU Yongqing, LIU Linlin, YE Yinghua. Study on the properties of multi-cell T-shaped concrete-filled steel tubular intermediate long columns under axial load [J]. China Civil Engineering Journal, 2012,45(9):27.
收稿日期:2015-12-02
基金项目:国家自然科学基金(51208375)
通讯作者:雷敏(1977—),男,工学博士,主要研究方向为组合结构. E-mail:leimin77@163.com
中图分类号:TU317.1;TU392
文献标志码:A
Experimental Investigation on Concrete-filled T-shaped Steel Tube Stubs Subjected to Axial Compression
CHEN Yu1, SHEN Zuyan1,2, LEI Min3, LI Yuanqi1,2
(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2.State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China; 3.School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract:Tests were conducted on six concrete-filled T-shaped steel tube (CFTST) stubs to investigate the characters of the deformation, failure modes and the bearing capacity of this kind of composite columns. The parameters taken into consideration in the test included the depth to thickness ratio of steel plates, the cross sectional depth to width ratio of the specimens. Experiment indicated that the bearing capacities of CFLST columns were not improved effectively, but the ductility were increased considerably, due to the fact that the local buckling mode of steel tubes were altered by the core concrete. It was also observed that the outward corners of steel tubes gave the greater confinement to concrete, and the inner corners almost failed to confine the core concrete due to the separation between the steel plate and the core concrete; hence CFTST stub columns failed in the local buckling of the wider steel plate and the crushing of concrete in the region of local buckling and inner corner. Test results showed that the decrease of the depth to thickness ratio of the flange plates of the steel tubes could postpone the occurrence of the initial local bucking in the wider steel plate, strengthen the confinement effects of steel tubes on concrete, and enhance the bearing capacity and ductility of the CFTST columns. Finally, the applicability of the methods in current specifications or codes, national and abroad, for calculating the bearing capacity of specimens was discussed.
Key words:concrete-filled T-shaped steel tube; axial compression; stub; depth to thickness ratio of steel tube; local buckling; bearing capacity
第一作者: 陈雨(1976—),男,博士生,主要研究方向为钢结构. E-mail:carton716257@163.com

