大尺寸抛物线形超声变幅杆频率的瑞利修正

张宁宁

(渭南师范学院 物理与电气工程学院,陕西 渭南 714000)



大尺寸抛物线形超声变幅杆频率的瑞利修正

张宁宁

(渭南师范学院 物理与电气工程学院,陕西 渭南 714000)

摘要:利用瑞利能量法对大尺寸抛物线形超声变幅杆的共振频率进行修正,得到了修正频率表达式．通过数值计算得出大尺寸抛物线形超声变幅杆频率修正结果,并利用有限元软件对一组大尺寸抛物线形变幅杆进行模态分析．将修正结果与一维的理论值进行对比分析,可得修正后的频率值更接近于有限元模拟仿真值．

关键词:大尺寸抛物线形超声变幅杆;共振频率;瑞利修正;有限元模拟

0引言

超声变幅杆在功率超声振动系统中非常重要,其主要作用是放大质点机械振动的位移或速度,或将超声能量集中在较小的面积上．在超声变幅杆领域中，指数形变幅杆、圆锥形变幅杆、悬链线形变幅杆、阶梯形变幅杆等单一及各种复合振动变幅杆的特性得到众多学者的研究[1-5]．单一变幅杆中,圆锥变幅杆的因数最大,但放大系数最小．文献[6]研究了一种抛物线形变幅杆,与圆锥形变幅杆相比较,抛物线形变幅杆具有放大系数较大,形状因数可比的优点．传统变幅杆设计一般按照一维理论,当变幅杆横向尺寸小于1/4波长时,可以忽略横向振动对纵向频率造成的影响．但在许多需要大功率、高声强的功率超声应用领域中,通常需要一种横截面积大的变幅杆来获得较大的功率和声强．而此时,由于泊松效应的影响,横向的振动不可忽略,传统设计理论的结果将会出现较大的误差．文献[7-10]分别修正了大尺寸的指数形、悬链型和有孔圆锥变幅杆的频率,理论计算与模拟结果较符合.文献[11]分析了大尺寸矩形截面抛物线型变幅杆,对固有频率进行修正,但是局限在矩形截面的块状振动体上,对于大截面的回转体变幅杆很难用解析法来分析,特别是对圆截面抛物线型变幅杆未见研究．本文利用瑞利能量法推导出圆截面大尺寸抛物线形变幅杆的频率修正结果,通过有限元软件Ansys进行模态分析．结果表明,利用瑞利能量法修正得到的频率,与一维理论值相比较,更接近于有限元模拟仿真值．

1频率方程

对于均匀各向同性材料构成的变截面变幅杆,不考虑机械损耗,并设横截面上应力分布均匀[1],则所求动力学方程为

(1)

(2)

(3)

由式(3)可得其应变分布的函数为

(4)

(5)

根据式(5)可计算变幅杆一维纵振动频率．

2共振频率的瑞利修正

在大尺寸匀质超声变幅杆做纵向振动时,由于泊松效应的影响,必然存在横向振动,且横向振动较为强烈不可忽略,并对纵向振动有明显的影响,而且横向尺寸越大对纵向振动的影响越大．从振动能量角度进行分析,传统的一维设计理论只考虑了纵向振动下变幅杆的势能和动能,而在大尺寸变幅杆中,较强的横向振动会引起振动系统动能增加,从而增加系统的惯性,使变幅杆的等效分布参数发生变化,最终引起纵向振动的波速减慢,共振频率降低．采用瑞利能量法的近似理论假设,可认为形变前后在同一截面的质点仍旧处在同一平面上,即纵向位移ξx和半径r关;径向形变是均匀的,即径向位移与半径成正比,且两种振动是同相位的．因此可以得到,变幅杆在径向上的应变方程为

(6)

其中σ是泊松系数,εr是径向应变,εx是纵向应变,且ξx是纵向位移.又由于其应变均匀,即径向的位移ξr=rεr,则其径向位移的函数为

(7)

其径向振速的函数为

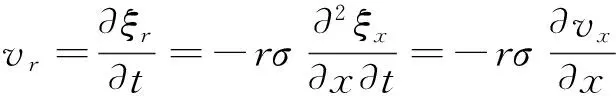
(8)

由于圆截面上变幅杆质点振动位移关于中心轴是对称的,因此轴对称上环带微元的质量可表示为

dm=ρdrds=2πρrdrdz.

(9)

由动能定理环带微元的纵向振动引起的能量为

(10)

由于横向振动的影响,该振动系统所引起的横向的能量为

(11)

设系统在一维纵振过程中的等效质量为me,由于横向振动的影响,动能增加后的等效质量的增量为Δme,则有

(12)

由式(12)可得,当考虑变幅杆在横向振动时,该振动系统所对应的等效的质量就会增大．由于共振频率和系统对应的等效质量平方根的大小成反比,则得

(13)

对于抛物线形变幅杆由式(3)及(4)可知,在两端自由的条件下，纵向振速vx及其对x的一阶偏导为

(14)

(15)

其中A是常数,且φ是初相位．

将式(14)，(15)及R(x)=R1(l-ax)2带入式(10)，(11),并令初相位φ=0，可得

(16)

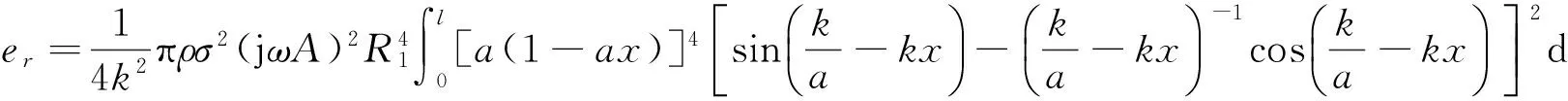
(17)

将式(16)，(17)代入式(13)可得修正后频率方程．若给定变幅杆的各项尺寸和材料参数,可由式(5)计算出纵振动频率,再由修正后的频率方程计算可得修正后的频率．

3有限元模拟

随着计算机和数值计算方法的高速发展,应用有限元法来预测复杂振动系统的振动特性变得越来越重要．有限元法能够对超声振动系统进行精确建模,利用Ansys有限元分析软件可以简化从建模到提取参数的一系列过程,不仅可以分析系统的振动模式和共振频率,而且可以给出振动系统在任意位置及时刻的应力和应变状态以及位移分布[12-15]．为了验证本文中所得结论的精确性,取变幅杆材料为45号钢,其杨氏模量E=2.06×1011,泊松系数σ=0.28,密度ρ=7.84×103kg·m-3．表1为抛物线形变幅杆的理论值与Ansys有限元模拟值的比较．其中N为变幅杆大小端面积比,R1,R2分别为大小端半径,f1为一维纵振动频率,f2为修正后的理论计算频率,f3为有限元模拟频率,Δf1，Δf2分别为纵振动频率及修正后的理论频率与有限元模拟结果的百分误差．

表 1　抛物线形超声变幅杆的理论值和模拟值的比较

由表1可以得出,当径长比R1/l较小时,其理论频率值和有限元模拟值的差异较小,若其径长比增大,则误差也随之增大．通过能量法修正后的值比一维理论值更接近于有限元模拟值,误差比较可以看出,修正后的频率误差相对较小．但在其径长比超出一定的范围时,其修正后的值与模拟仿真值之间的误差也比较大.所以当径长比超出一定值时,瑞利近似理论将不再适用．文中在有限元模态分析中发现当R1>66.67mm，即径长比大于0.5时, 得到的振动模态中伴随有弯曲振动,当R1再增大时,其弯曲振动及扭转振动所呈现的效果将越明显,此时瑞利能量法的近似理论不再适用．当取R1=60 mm 时,没有发现明显的弯曲振动或者扭转振动的现象,因此取径长比R1/l<0.5．

4结束语

通过瑞利能量法对大尺寸抛物线形变幅杆的共振频率进行修正,得出了大尺寸抛物线形变幅杆的纵振频率修正公式．对比分析可知,考虑横向振动的影响，修正后的结果比一维理论值更接近有限元模拟值,且变幅杆的尺寸越大其修正的效果越明显.但当径长大于0.5时瑞利近似理论不再适用.其结果为超声加工振动系统的设计及频率调节提供参考依据．

参考文献(References):

[1]林仲茂.超声变幅杆的原理及设计[M].北京:科学出版社,1987:53-196.

LIN Zhongmao.Principle and design of ultrasonic amplitude transformer[M].Beijing:Science Press,1987:53-196.

[2]刘战锋,李培繁,王天琦.超声复合变幅杆的设计与研究 [J].现代制造工程,2008,35(2):102-104.

LIU Zhanfeng,LI Peifan,WANG Tianqi.The design and research of ultrasonic composite solid horn[J].Modern Manufacturing Engineering,2008,35(2):102-104.

[3]贺西平,胡时岳.复合超声纵振型变幅杆的简化设计[J].兰州大学学报:自然科学版,2002,38(5):24-26.

HE Xiping,HU Shiyue.Simplified design methods for composite ultrasonic longitudinal vibration horn[J].Journal of Lanzhou University:Natural Science Edition,2002,38(5):24-26.

[4]伍利群.变幅杆的外形结构对超声纵向振动性能参数的影响[J].机械设计与制造,2010(4):212-213.

WU Liqun.The influence of horn shape size change on the performance of ultrasonic longitudinal vibration[J].Mechinery Design and Manufacture,2010(4):212-213.

[5]陈秀梅,林书玉,鲜晓军.抛物线型超声变幅杆的探讨[J].声学技术,2007,26(5):1295-1299.

CHEN Xiumei,LIN Shuyu,XIAN Xiaojun.Study on a new parabolic transformer[J].Technical Acoustics,2007,26(5):1295-1299.

[6]张宁宁.余弦型扭转振动变幅杆的负载特性[J].纺织高校基础科学学报,2014,27(2):233-235.

ZHANG Ningning.Load characteristic of cosine-torsional vibration horn[J].Basic Sciences Journal of Textile Universities,2014,27(2):233-235.

[7]桑永杰,林书玉.基于能量修正法进行大尺寸指数型超声变幅杆准确设计[J].应用声学,2007,26(4):193-196.

SANG Yongjie,LIN Shuyu.Precise design of large dimension exponential ultrasonic amplitude transformer based on energy modification method[J].Applied Acoustics,2007,26(4):193-196.

[8]张鹏利,付志强,林书玉.悬链线形超声变幅杆共振频率的瑞利修正[J].陕西师范大学学报:自然科学版,2009,37(5):35-37.

ZHANG Pengli,FU Zhiqiang,LIN Shuyu.Rayleigh modification on the resonance frequency of catenary horn[J].Journal of Shaanxi Normal University:Natural Science Edition,2009,37(5):35-37.

[9]付志强,林书玉.大尺寸余弦形超声变幅杆的设计[J].声学技术,2008,27(5):765-768.

FU Zhiqiang,LIN Shuyu.Design of cosine type ultrasonic transformers[J].Technical Acoustics,2008,27(5):765-768.

[10]刘洋,郑建新,刘传绍.大截面超声珩磨圆锥型变幅杆设计[J].机械设计,2013,30(9):62-65.

LIU Yang,ZHENG Jianxin,LIU Chuanshao.Design of conical horn with large section used in ultrasonic horning[J].Journal of Machine Design,2013,30(9):62-65.

[11]高健,张鹏利,林书玉.大尺寸抛物线型变幅杆的研究[J].声学技术,2009,28(2):53-54.

GAO Jian,ZHANG Pengli,LIN Shuyu.Study on a large dimension of parabolic transformer[J].Technical Acoustics,2009,28(2):53-54.

[12]梁召峰,周光平,张亦惠.ANSYS在功率超声领域中的应用[J].机械与电子,2005(8):10-13.

LIANG Zhaofeng,ZHOU Guangping,ZHANG Yihui.Application of ANSYS in the field of power ultrasound[J].Mechinery and Electronics,2005(8):10-13.

[13]朱伯芳.有限单元法原理与应用[M].北京:水利电力出版社,1979:82-96.

ZHU Bofang.Principle and application of finite element method[M].Beijing:Water Conservancy and Electric Power Press,1979:82-96.

[14]廖伯瑜,周新民,尹志宏.现代机械动力学及其工程应用[M].北京:机械工业出版社,2004:86-92.

LIAO Boyu,ZHOU Xingmin,YIN Zhihong.Modern mechanical dynamics and its application in engineering[M].Beijing:Machinery Industry Press,2004:86-92.

[15]李皓月,周田朋,刘相新.ANSYS工程计算应用教程[M].北京:中国铁道出版社,2003:65-78.

LI Haoyue,ZHOU Tianpeng,LIU Xiangxin.ANSYS engineering calculation application tutorial[M].Beijing:China Railway Press,2003:65-78.

编辑、校对：师琅

文章编号:1006-8341(2016)02-0217-05

DOI：10.13338/j.issn.1006-8341.2016.02.014

收稿日期：2015-10-28

基金项目:陕西省教育厅自然科学专项基金资助项目(2013JK0615);渭南师范学院科研育苗项目(15YKP009)

作者简介:张宁宁(1978—),女,陕西省西安市人,渭南师范学院讲师,研究方向为功率超声及应用. E-mail:zhangning7892@163.com

中图分类号：TB 556

文献标识码：A

Rayleigh correction of the frequency of large size parabolic ultrasonic horn

ZHANGNingning

(Physical and Electrical Engineering Institute, Weinan Teachers University,Weinan 714000,Shaanxi,China)

Abstract:The resonance frequency of large size parabolic ultrasonic horn was corrected by using the Rayleigh energy method, and the expression of modified frequency parabolic horn was obtained.By numerical calculation,large size parabolic horn frequency correction results was obtained,and by finite element analysis software, a group of large size parabolic horn was simulated. The modified results and one-dimensional theoretical values were compared and analyzed,it shows that and the frequency is adjusted close to the finite element simulation results.

Key words:large size parabolic ultrasanic horn; resonant frequency; Rayleigh correction; the finite element simulation

引文格式：张宁宁.大尺寸抛物线形超声变幅杆频率的瑞利修正[J].纺织高校基础科学学报,2016,29(2)：217-221.

ZHANG Ningning.Rayleigh correction of the frequency of large size parabolic ultrasonic horn[J].Basic Sciences Journal of Textile Universities,2016,29(2):217-221.