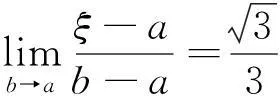拉格朗日中值定理中值点的确定与渐进性*

李治远

(云南大学 数学与统计学院，云南 昆明 650500)



拉格朗日中值定理中值点的确定与渐进性*

李治远

(云南大学 数学与统计学院，云南 昆明 650500)

摘要:文章先对几类初等函数的拉格朗日中值定理中值点进行讨论，然后又过渡到对一般的连续可导函数中值点的渐进性讨论.

关键词:拉格朗日中值定理；中值点；渐进性

拉格朗日中值定理的使用非常普遍，但是它只肯定了中值点的存在性，中值点的位置并没有被具体确定.本文总结了几类初等函数的拉格朗日中值定理中值点的确定方法，并在此基础上探讨了从低阶可导到高阶可导函数的拉格朗日中值点的渐进性质.这让我们对拉格朗日中值定理有了更深一步的认识与理解.中值点的确定方法以及渐进性质在实际应用中也是非常重要的.

1初等函数拉格朗日中值定理中值点确定

定理1对任意的幂函数f(x)=xn(n>0),x∈[a,b]，其中0

推论1对任意的幂函数f(x)=xn(n<0),x∈[a,b]，其中0

定理2对任意的指数函数f(x)=μx(μ>0,μ≠1)，其中x∈[a,b].若θ满足

定理4对任意三角函数f(x)=sinx，x∈[a,b]，若θ满足

2拉格朗日中值定理中值点的渐进性

证明由泰勒公式，得

f(b)=f(a)+f'(a)(b-a)+

由拉格朗日中值定理，有

f'(ξ)(b-a)

f(x)=f(a)+f'(a)(x-a)+

f(b)=f(a)+f'(a)(b-a)+

由拉格朗日中值定理有

证明由泰勒公式和定理条件，得

f(x)=f(a)+f'(a)(x-a)+

于是有

f(b)=f(a)+f'(a)(b-a)+

由拉格朗日中值定理，得

参考文献：

[1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2002.

[2]吴良森.数学分析习题精解[M].北京:科学出版社,2001.

[3]吉米多维奇.数学分析习题集题解[M].济南:山东科学技术出版社,2001.

(责任编辑:陈衍峰)

DOI:10.13877/j.cnki.cn22-1284.2016.06.010

*收稿日期：2015-10-12

基金项目：国家自然科学基金“复杂数据下众数回归模型的变量选择及统计诊断研究”(11561075)

作者简介：李治远,河南信阳人,云南大学数学与统计学院在读硕士.

中图分类号：O171

文献标志码：A

文章编号：1008-7974(2016)03-0027-02