双旋静稳定弹的共振不稳定研究

张衍儒 肖练刚 邱 奕 周 华

北京航天自动控制研究所，北京 100854



双旋静稳定弹的共振不稳定研究

张衍儒 肖练刚 邱 奕 周 华

北京航天自动控制研究所，北京 100854

由于双旋弹的鸭舵和弹体相对旋转，非对称固定翼鸭舵方位角的改变干扰了双旋弹角运动的周期，如果这个干扰的频率与弹体自由摆动的频率相同就会发生共振，共振的出现使攻角突增或发散，造成飞行不稳，这种不稳定称为共振不稳定。本文分析了双旋静稳定弹角运动方程，讨论了共振不稳定的特性。研究可知，攻角运动的振幅与固定翼鸭舵的转速和双圆运动的两个频率有关，固定翼鸭舵转速的不合理可能引起攻角运动的发散，而保持固定翼鸭舵转速远离双圆运动2个频率可以有效避免双旋弹的共振不稳定。

双旋静稳定弹；共振不稳定；固定翼鸭舵；双圆运动

近年来，由于制导武器的低成本和小型化需要，双旋静稳定弹被作为一个主要的研发方向，进行了多次实弹研发。例如，MGK型120mm双旋制导迫击炮弹[1]、RCFC型81mm双旋制导迫击炮弹[2]、RCFC型120mm双旋制导迫击炮弹[2]和RCFC型挂飞制导炸弹[3]。

图1 双旋静稳定弹的实弹示例

上述双旋静稳定弹的飞行稳定性可以通过弹体外形的静稳定特性实现，但是攻角的变化规律与鸭舵转速的对应关系缺少理论方面的介绍，本文探索并研究了攻角运动振幅与固定翼鸭舵转速的对应关系，最终提出了有效避免双旋弹共振不稳定[4]的控制方案。

1 双旋静稳定弹的控制原理

传统基于十字鸭舵的6自由度控制方式，虽然可以精确实现横法向过载修正，但是整体设计成本较高，为了降低成本，改装鸭舵为固定翼鸭舵，固定翼鸭舵由2对固定舵角的舵片组成，其中1对舵片的偏转方向相反，用于提供鸭舵反向旋转所需的外部气动导转力矩，如图2中滚转舵片1和3；另一对舵片的偏转方向相同，用于提供弹体姿态调整的气动控制力矩矢量，如图2中俯仰舵片2和4。

图2 双旋弹的绕质心运动

固定翼鸭舵通过内部的轴承绕弹体纵轴旋转，当固定翼鸭舵的滚转角速度为0时，固定翼鸭舵相对弹体纵轴静止。此时固定翼鸭舵的俯仰舵片产生鸭舵气动控制力，考虑绕质心运动，可以得到鸭舵气动控制力矩。由于双旋弹为静稳定弹，因此弹体压心在质心后，考虑弹体绕质心的动力学方程，可知弹体静力矩和鸭舵气动控制力矩能够满足力矩平衡条件，使双旋弹产生相应的合成攻角。考虑全弹质心运动的动力学方程，可知弹体纵轴向鸭舵气动力矢量方向移动，根据上述原理实现双旋弹的制导飞行控制。

2 推导双旋弹攻角运动方程

双旋弹制导飞行时，主要有鸭舵旋转和鸭舵静止2个状态，其中鸭舵旋转状态用于双旋弹的导航姿态初始化[5]，与共振不稳定相关，鸭舵静止状态用于制导飞行控制，与静稳定特性相关。

为了方便攻角运动方程推导，引入以下符号：

(1)

(2)

弹体纵轴相对理想弹道的高低角和方向角分别为φpc=φpg-θ和εpc=εpg，简化绕质心运动的动力学方程为：

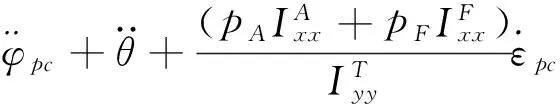
(3)

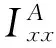
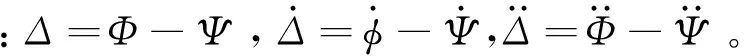
将式(2)写为复数形式，忽略重力侧向力(gsinθΨ=0)可得：

(4)

将式(3)写为复数形式可得：

(5)

由式(4)求导数可得：

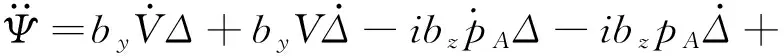
(6)

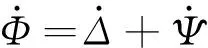
(7)

(8)

(9)

(10)

利用上述符号，简化合成攻角Δ关于弧长s的表达式为：

(11)

3 固定翼鸭舵旋转时攻角变化规律

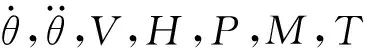
Δ=ΔPA+ΔPg+ΔPF

(12)

二圆角运动的齐次方程通解为：

ΔPA=C1eiω1s+C2eiω2s

(13)

式中：系数C1和C2由初始条件决定；ω1和ω2为齐次方程的特征根，也是双圆运动的频率，即弹体的自由摆动的频率，忽略小量PT和T可得：

(14)

考虑由固定翼鸭舵引起的角运动，由式(11)可知角运动方程可写为：

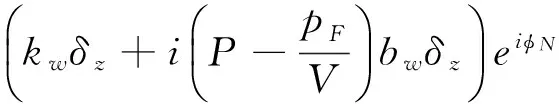
(15)

假设固定翼鸭舵转速pF为常值，不考虑起始滚转角所造成的差异，当pF(s)=pF/V而不等于齐次方程特征频率ω1,2时，式(15)的非齐次特解可写为如下形式：

ΔPF=KφNe-ipF(s)s

(16)

将式(16)带入式(15)中，可解出：

(17)

略去数值较小的马格努斯力矩项T和阻尼项H，同时注意到kwδz≫(P-pF(s))bwδz，KφN可近似为：

(18)

因此，当固定翼鸭舵以转速pF匀速旋转时，攻角受迫运动规律可近似为等幅周期运动，幅值大小为KφN，周期为pF(s)。

4 共振不稳定仿真试验

仿真验证攻角运动振幅与固定翼鸭舵转速的对应关系，即式(18)是否正确。分别测试pF为-2π(°)/s，-π(°)/s时实际攻角T_alpha的幅值与通过式(18)计算得到的估计幅值KφN是否一致，仿真结果如图3所示。

图3 攻角估计值K与实际攻角T_alpha幅值的对比曲线

由图3可知，实际攻角T_alpha幅值变化规律与理论值吻合较好，合成攻角的幅值可以通过式(18)求取的估计值K近似得到。

图4 双旋静稳定弹的攻角双圆运动

图5 实际攻角T_alpha幅值随固定翼鸭舵转速变化趋势

由图5可知，合成攻角T_alpha的幅值会在pF(s)与ω1,2趋于一致时不断增大，呈现出发散的趋势，从而产生共振不稳定。

通过上述分析可知，可以调节固定翼鸭舵的滚转角速度pF实现合成攻角T_alpha的幅值变化，该项技术可用于固定翼鸭舵的姿态初始化过程中。需要注意的是，固定翼鸭舵消旋进入X轴陀螺仪量程范围的过程中，应该快速通过双旋弹的共振频率，避免引起双旋弹的共振不稳定，如图6所示。

图6 有效避免双旋弹共振不稳定的过程

由图6可知，固定翼鸭舵转速通过共振不稳定转速频率时，攻角会有一个增大的过程，固定翼鸭舵的滚转控制算法应使鸭舵转速快速通过共振区域，从而有效避免双旋弹的共振不稳定。

5 结论

通过双旋静稳定角运动方程研究固定翼鸭舵制导炮弹的共振不稳定性，通过数学推导与仿真分析，得出固定翼鸭舵的转速及双圆运动频率影响攻角运动，其中，固定翼鸭舵转速是关键，设计时使其远离双圆频率可以避免共振不稳定性。

[1] Kelly Hanink. Mortar Guidance Kit (MGK) [R]. America: 2010 Joint ArMaments Conference, 2010.

[2] Yousef Habash. Roll Control Guided Mortar (RCGM) [R].America: NDIA Joint ArMaments Conference, 2012.

[3] Asad Khan. Project Overview-Precision Air Dropped Guided Munition(PADGM) [C]. America: 46th Annual Gun & Missile Systems Conference & Exhibition, 2011.

[4] 韩子鹏. 弹箭外弹道学[M].北京: 北京理工大学出版社，2008：261-273.(Han Zipeng. Rocket Exterior ballistics [M].Beijing Institute of Technology press, 2008:261-273.)

[5] 张衍儒, 肖练刚. 旋转控制固定鸭舵的导航初始化与控制算法研究[J].航天控制, 2014, 32(6):35-39.(Zhang Yanru, Xiao liangang. Navigaion Initialization and Control Algorithm of Roll Control Fixed Canards[J]. Aerospace Control, 2014, 32(6):35-39.)

Research on Resonance Instability of Dual-Spin Static Stability Projectile

Zhang Yanru, Xiao Liangang, Qiu Yi, Zhou Hua

Beijing Aerospace Automatic Control Institute, Beijing 100854，China

Duetotherelativerotationbetweenthecanardsandthebodyofthedual-spinprojectile,theangularperiodicdisturbanceofthedual-spinmotionisformedbytherotationoffixedcanards.Ifthefrequencyisthesameasthebodyvibrationfrequency,theresonanceoccursandthentheangleofattackisincreasedbyresonancewhichresultsinflightinstability,therefore,thisinstabilityiscalledresonanceinstability.Inthispaper,thecharacteristicsofresonantinstabilityareresearchedbyanalyzingtheangularmotionequationofdual-spinstaticstabilityprojectile.Astheresearchreveals,theamplitudeoftheangleofattackisrelatedtothespeedofthefixedcanardsandthetwofrequenciesoftwo-circlemovementandthedivergenceoftheattackangleiscausedbytheunreasonablespinspeedoffixedcanards,andwhenthespinspeedofthefixedcanardsisfarfromthetwofrequenciesoftwocircularmotion,theresonanceinstabilitycanbeavoidedeffectively.

Dual-spinstaticstabilityprojectile;Resonantinstability;Fixedcanards;Twocirclemovement

2015-09-21

张衍儒(1985-)，男，哈尔滨人，博士，工程师，主要研究方向为制导弹药控制系统综合；肖练刚(1973-)，男， 四川资中人，博士，研究员，主要研究方向为导航、制导与控制；邱 奕(1990-)，男，四川重庆人，硕士，助理工程师，主要研究方向为导航、制导与控制；周 华(1989-)，男，湖南衡阳，硕士，助理工程师，主要研究方向为导航、制导与控制。

TJ412.+1

A

1006-3242(2016)03-0031-05