深基坑格形地连墙支护结构变形与土压力研究

王　飞，刘亚文，苏静波，冯　斌，贾　顺，梁进军

(1.解放军理工大学野战工程学院，江苏 南京　210007；2．河海大学港口海岸与近海工程学院，江苏 南京　210098；3.南京重大路桥建设指挥部，江苏 南京　210000)



深基坑格形地连墙支护结构变形与土压力研究

王飞1，刘亚文1，苏静波2，冯斌3，贾顺3，梁进军1

(1.解放军理工大学野战工程学院，江苏 南京210007；2．河海大学港口海岸与近海工程学院，江苏 南京210098；3.南京重大路桥建设指挥部，江苏 南京210000)

摘要：为了对格形地连墙的受力和变形特征进行系统研究，针对南京某基坑工程的格形地连墙支护结构，建立有限元分析模型，其中岩土材料采用Mohr-Coulomb弹塑性本构模型；通过数值模拟研究分步开挖时此类基坑的变形和土压力分布规律，并与实测数据和朗肯土压力进行对比；最后分析后墙及隔墙深度、后墙宽度、前墙厚度和内坑加固等因素的影响。分析表明：格形地连墙的侧向变形类似于悬臂梁变形，最大侧向变形位于墙顶，这一变形形态与常见多道支撑支护结构的变形规律存在差异，且前墙厚度和内坑被动区加固对此类支护结构性状的影响比较显著。

关键词：深基坑；格形地连墙；有限元分析；变形；土压力

0引言

随着对地下结构功能要求越来越高，常用的支护结构已经无法满足这些基坑工程的要求，近些年格形地连墙作为一种新型支护结构开始应用到基坑工程中。格形地下连续墙，简称格形地连墙，由前墙、后墙和隔墙组成，隔墙连接前、后墙构成的格形结构，和其区间土体形成半重力式结构，作为基坑支护结构时集挡土、止水和承重三效合一，同时其兼有地下连续墙刚度大、抗渗性能好、可以更好地限制基坑的变形，以及可以作为永久支护结构承担上部结构的竖向荷载等优点。

格形地连墙是一种自立式支护结构，起初被应用于大型船坞的永久性坞墙，随着技术的日臻成熟，逐渐被运用到建筑物地下结构、地铁、隧道、码头、护岸的挡土墙和防渗墙等领域[1]。然而在我国现行的国家规范JGJ 120—2012《建筑基坑支护技术规程》[2]中，均采用针对常规基坑支护结构的板式支护体系的弹性地基梁法，由于格形基坑本身的几何特性，该方法无法运用到以格形地连墙为支护结构的基坑工程的计算和设计中；同时，相对于格形地连墙应用于实际工程的时间来讲，其理论形成和研究仍处于起步阶段。仇建春等[3]以具体基坑工程为背景，建立有限元数值模型，模拟基坑施工过程，分析研究双排格形地连墙的空间变形特性，并得出地连墙的变形随着基坑开挖深度的增大而增大；周广柱等[4]通过离心模型试验模拟了分步开挖基坑时格形地连墙和软土的相互作用，并把测定结果与朗肯土压力进行比较，总结出格形地连墙墙体每个侧面的土压力基本上都呈线性分布，且随深度增加而增大的规律；梅英宝[5]对部分采用格形地连墙围护的某船坞基坑格形地连墙的实测水平变形进行了较为详细地分析，总结了格形地连墙围护结构水平变形的一些规律，指出了自立式格形地连墙变形计算存在的不足，提出了格形地连墙围护设计中仍需进一步研究的问题；夏建国[6]对格形地连墙结构的设计与施工方案进行验证，得出格形地连墙技术可行，使用前景广阔；时爱祥等[7]应用ABAQUS有限元软件，通过三维有限单元法模拟某基坑开挖过程，研究得出格形地连墙与一般地连墙的位移分布特征不同，墙顶位移较小，墙底位移最大；梁穑稼等[8]结合实际工程，采用离心模型试验和现场监测方法对格形地连墙侧向变形规律、设计参数对墙体位移的影响以及围护结构最大侧向位移与开挖深度的关系进行了分析，结果表明，墙顶水平位移较大，墙体发生重力式位移，前、后墙的变形规律相似。这些成果对于后续研究具有重要的参考和借鉴价值，然而在采用格形地连墙的工程中，其受力和变形特征还未得到系统的研究。本文以南京某基坑工程为背景，建立空间有限元分析模型并模拟实际分步开挖，通过数值模拟研究分步开挖时以格形地连墙为支护结构的基坑的变形和土压力分布规律，并与实测数据以及朗肯土压力进行对比，最后分析后墙及隔墙深度、后墙宽度、前墙厚度和内坑加固等因素的影响。

1工程实例

南京青奥轴线地下交通系统J匝道基坑长约110 m，宽约10.55 m，开挖深度为14.55～17.15 m，施工方法为明挖顺作法，施工现场位于长江夹江东南岸，属长江古河道漫滩地貌区，地层以灰褐色粉质黏土、粉土及淤泥质土为主。本次计算所取地质资料数据，根据勘察单位提供的地质报告如表1所示。基坑开挖采用大放坡加悬臂直立开挖的形式，先放坡开挖至-0.5 m(地面标高为7.5 m)，再进行直立开挖至坑底。基坑左侧采用格形地连墙支护结构，格形地连墙的具体尺寸如图1所示，右侧采用800@1 000钻孔灌注桩支护结构。基于工程典型断面监测数据建立动态反演系统获得土体弹性模量。基坑开挖时坑内采用了深井降水，施工过程中待格形地连墙达到设计强度后再开始基坑开挖，地面超载10 kPa。

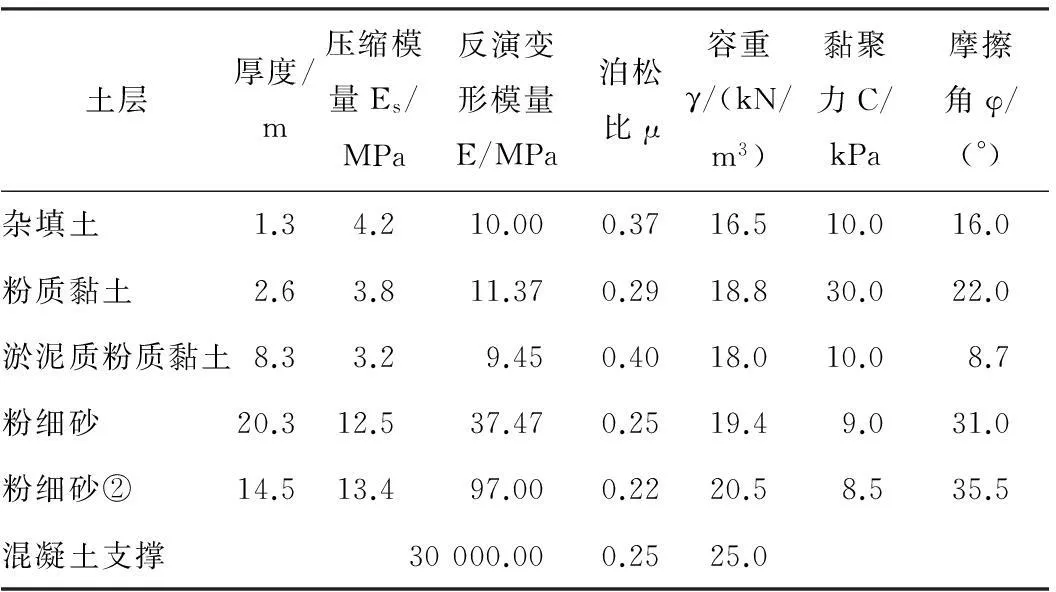
表1　土层、支撑物理力学性能指标

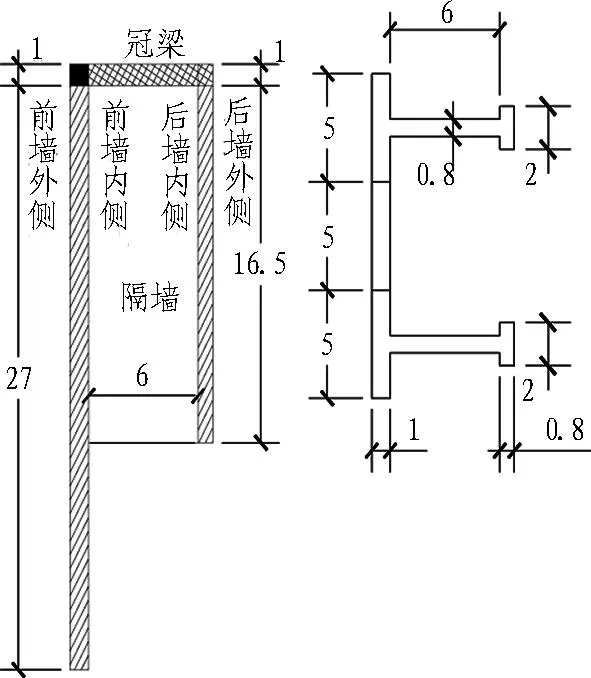
图1　格形地连墙详图(单位：m)

2有限元模型

鉴于以格形地连墙为支护结构的基坑在开挖过程中的受力和变形情况，现有的解析方法很难得出比较准确的解，本文采用MIDAS/GTS软件建立三维数值模型并综合考虑各种施工措施进行数值研究。

2.1基本假设

1)初始地应力场不考虑格形地连墙槽段施工所引起的地应力释放[1]。

2)假定在同一土层中，土是均匀的、连续的、各向同性的。格形地连墙等支护结构均按各向同性弹性材料考虑，土体采用Mohr-Coulomb弹塑性模型，格形地连墙以及各土层采用三维实体单元模拟。

3)基坑开挖期间不考虑降水、渗流和固结的影响[9]。

2.2模型建立

格形地连墙作为基坑的支护结构，自身具有明显的三维几何特征，平面应变有限元方法无法反映其前墙、后墙和隔墙组成的格形结构的空间效应。本文在综合考虑格形地连墙自身几何特征和工程影响范围的基础上建立空间三维模型。模型自前墙向后延伸35 m，自坑底向下延伸32 m，共划分37 626个单元(见图2)。模型边界条件为：左、右边界X方向位移为0；下边界X、Y、Z方向位移均为0；前、后边界Y方向位移为0；其他边界位移自由。

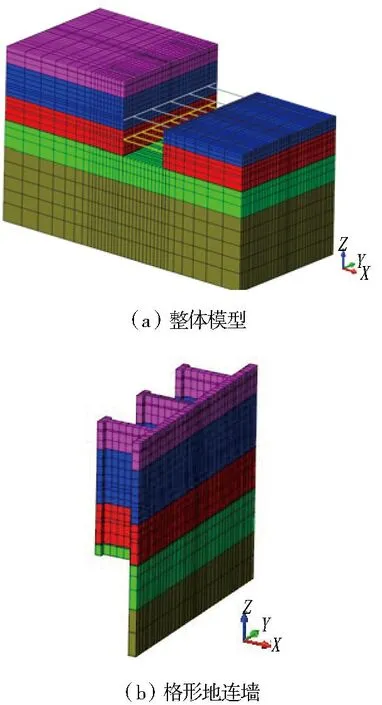
图2　三维有限元模型

2.3工况模拟

深基坑开挖需进行分步开挖以求得基坑工程在不同开挖深度下的变形效应，为此将整个基坑开挖过程分为4个计算工况。各工况定义如下：1)放坡开挖至3.9 m(地面标高为7.5 m)，即开挖深度为3.6 m；2)放坡开挖至外坑坑底-0.5 m处，即开挖深度为8.0 m，同时施作混凝土支撑；3)直立开挖至-5.1 m处，即开挖深度为12.6 m，同时架设第1道钢支撑；4)直立开挖至内坑坑底-8.5 m处，即开挖深度为16 m。在MIDAS/GTS软件中通过“激活”和“钝化”单元组的形式模拟各工况。

3有限元计算结果分析

3.1格形地连墙的变形性状分析

不同工况下格形地连墙的变形情况见图3。由图3(a)、(b)可知，在放坡开挖阶段，仅依靠格形地连墙承担坑外土压力；因此，格形地连墙的侧向变形类似于悬臂梁变形，最大侧向变形位于墙顶，这一变形形态与常见多道支撑支护结构呈“两头小、中间大”式的“大肚”状的变形规律[10]存在差异，在整个开挖过程中前、后墙沿着深度产生相对水平变形，但由于格形地连墙整体性较好，其相对变形较小。前墙在墙顶以下1/5墙体深度内的位移基本上接近墙顶最大位移,往下逐步减小；而后墙的侧向变形略小于前墙,且在墙顶即开始往下减小。随着开挖深度加大,前、后墙的水平位移变化规律和幅度基本一致。

(a) 前墙水平位移

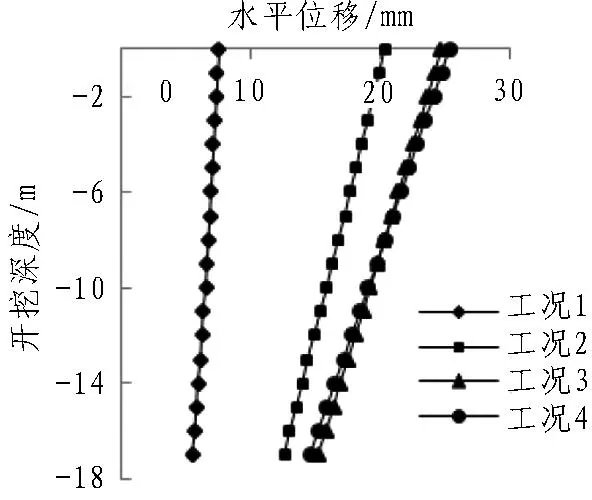
(b) 后墙水平位移

(c) 格形地连墙最大侧向变形与开挖深度的关系

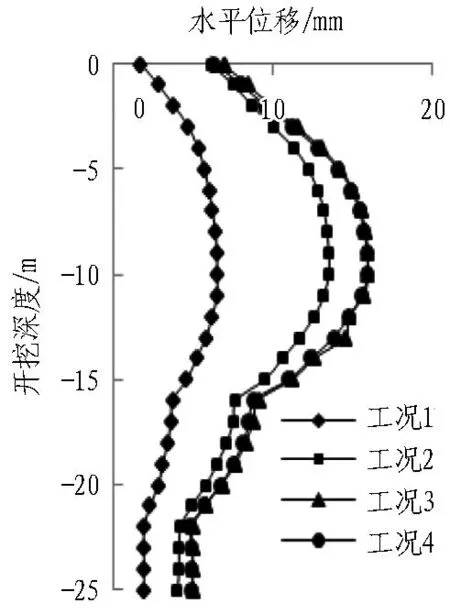
(d) 坑后15 m处土体水平位移

图3(c)表示格形地连墙的最大侧向变形δ与基坑开挖深度H的关系。工况1(H=3.6 m)时，格形地连墙最大侧向变形为9.5 mm，δ/H≈0.26%；工况2(H=8 m)时，格形地连墙最大侧向变形为20 mm，δ/H=0.25%；工况3(H=12.6 m)时，格形地连墙最大侧向变形为24.7 mm，δ/H≈0.2%；工况4(H=16 m)时，格形地连墙最大侧向变形为25.4 mm，δ/H≈0.16%。可见随着开挖深度的增大，格形地连墙最大侧向变形亦不断增大，但最大侧向变形与开挖深度的比值却不断减小。将各工况下格形地连墙最大侧向变形的实测值与计算值作线性拟合，得到模型计算的最大侧向变形与开挖深度呈δ=0.183 9%H，而实测的最大侧向变形与开挖深度呈 δ=0.154%H，产生这种差异的主要原因是实际施工过程中充分考虑土体“时空效应”影响，采用分区开挖，及时架设支撑、浇筑各分区的基坑底板等，从而有效地减小了格形地连墙的最大侧向变形。

图3(d)为各工况下坑后15 m处土体水平位移沿深度变化情况，随着离基坑的距离增大，坑后土体的水平位移在减小，此时土体变形与常见多道支撑支护结构呈“两头小、中间大”式变形规律类似，究其原因可能是：距离格形地连墙较远，受其空间效应的影响较小，此时格形地连墙的作用类似于常规“一”字型地连墙。

3.2格形地连墙的受力性状分析

图4为不同工况下前、后墙的主动和被动土压力分布情况。随着工程的展开，坑外土体不断向坑内产生水平位移，主动区土体水平应力不断释放，致使前、后墙主动土压力随着开挖深度的增加而不断减小，其数值均小于静止土压力；但前、后墙的被动区土体随着开挖深度的增加而不断增大，且均大于静止土压力。由于前、后墙的相对变形较小导致格形结构内部的墙芯土体基本呈整体平动状态，受挤压作用较小，因此随着开挖深度的增加，后墙被动土压力、前墙主动土压力变化相对较小，这与侯永茂[1]的研究规律一致。此外前、后墙交界处由于应力集中导致前墙两侧的土压力均产生了突变。

3.3与实测数据的比较

在基坑开挖过程中，地连墙的变形与基坑、周边建筑物、地下管线的稳定和安全息息相关，必须使其最大位移不超过最大安全容许值。因此施工过程中在支护结构周边设置了测斜管，以监测支护墙和地基土体在各深度的水平位移。现将工况2、4的计算值与实测值作对比(见图5)，由图5可知各工况下各测点处侧向变形均呈悬臂状态，最大侧向变形位于墙顶，这与前述分析结果吻合；但实测结果较计算结果略小,主要原因可能是基坑中已作基底加固、搅拌桩止水帷幕及结构基础桩等，而计算中未考虑这些因素的影响。

由于我国文化、经济、政治在不同时期的发展都呈现出了不同的趋势，因此机关事业单位在展开工作时，其也应该重视会计理论体系的建设，也只有这样才能满足社会发展的需要。通常情况下，在实际工作中机关事业单位领导可以从单位的实际运行情况入手，然后结合社会发展现状来展开调整，可以在原有的基础上进行适当改革，目的是为了制定出一份满足单位实际发展需求的理论体系，并把其落实到每一个岗位上，为管理会计的应用提供一定的理论支持。

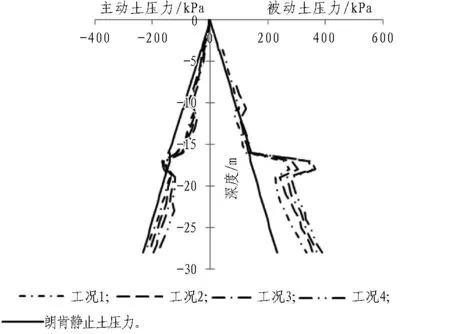
(a) 前墙两侧土压力

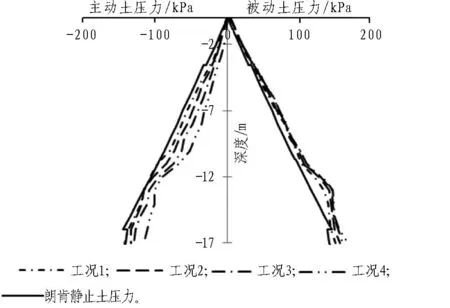
(b) 后墙两侧土压力

图5　计算值与实测值对比

Fig.5Comparison between calculated horizontal deformation and measured horizontal deformation

4参数敏感性分析

以前述参数建立的源模型为参考，进一步分析后墙及隔墙深度、后墙宽度、前墙厚度和内坑土体加固等因素对格形地连墙性状的影响。下述讨论中选用工况4计算结果作为比较。

4.1后墙及隔墙深度h的影响

假设其他因素保持不变，分别考虑后墙及隔墙的深度h为17.5、12.5、7、0 m(常规地连墙)4种情况，计算结果与源模型结果对比如图6所示。基坑开挖过程中h取不同值时格形地连墙变形特性相同，基本呈悬臂侧移，最大侧向变形均位于墙顶。随着h的减小在墙顶下1/6墙体深度内墙体的水平位移略有增大，而1/6～1/2墙深范围内墙体水平位移变化较大。说明增大后墙及隔墙的深度h对减小基坑土体位移有一定作用。由图6(b)可知，h=0时最大水平位移显著增加，说明相对于常规地连墙，格形地连墙空间整体性的优势更加明显。减小h后，作用在后墙上部区域的主动土压力不断减小，但在后墙的下部区域土压力却不断增大，恰似组成了抵抗格形地连墙翻转的力矩；因此，可以认为后墙发挥着向后拉拽前墙的作用，以减小前墙向基坑方向的倾斜，这与周广柱等[4]基于离心试验所得结论相同。

(a) 前墙水平位移的变化规律

(b) 最大水平位移随h的变化规律

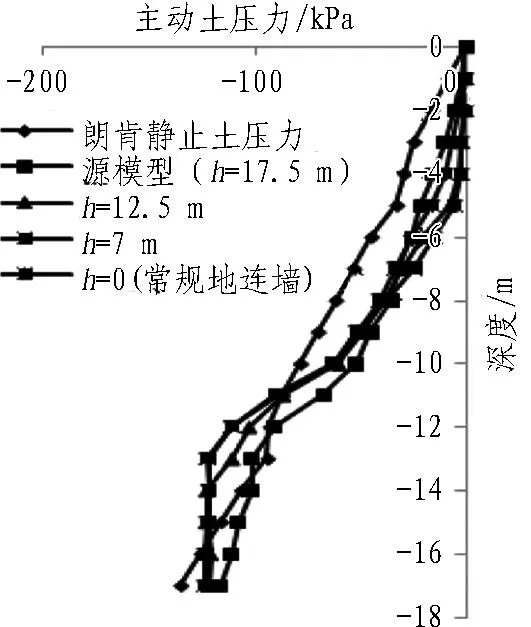
(c) 后墙主动侧土压力变化规律

Fig.6Effects of depth of backwall and separating wall on deformation of underground diaphragm wall

4.2后墙宽度b的影响

后墙宽度b分别取6、4、0 m(当b=0时，格形地连墙仅由隔墙和前墙组成，此时应视为T型地连墙[11-12])，将计算结果与源模型结果作对比(见图7)。由图7(a)可知，增加后墙宽度，墙体水平位移略微减小。现定义ξ=Δδ/Δb(Δδ为最大水平位移的增量；Δb为后墙宽度的增量)，以b=0为参考，计算可得ξ分别为 0.185%(b=2 m)、0.133%(b=4 m)和0.108%(b=6 m)。结合图7(b)可知，后墙宽度的增加，可以减小支护结构水平变形，但其作用效果却在不断降低。在实际工程中为减小支护结构水平变形，可以适当增加后墙的宽度，但需结合工程造价优化设计采用最优后墙宽度。增加后墙宽度，作用在后墙的土压力随之略有增大。

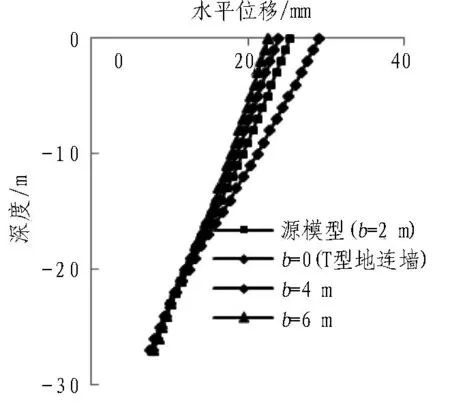
(a) 前墙水平位移的变化规律

(b) 最大水平位移随b的变化规律

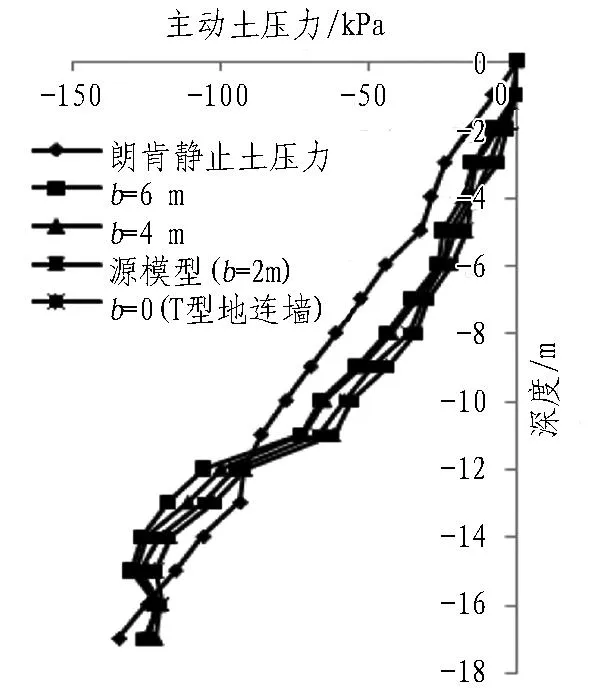
(c) 后墙主动土压力变化规律

Fig.7Effects of width of backwall on deformation of underground diaphragm wall

4.3前墙厚度t的影响

南京地区常用的地连墙厚度为0.6、0.8、1.0 m，在参数敏感性分析中再加入厚度0.9 m。计算过程中仅前墙厚度t改变，其他因素保持不变，计算结果见图8。随着t的增大，墙体刚度变大，墙体水平位移呈现不断减小的趋势，最大水平位移由t=0.6 m时的36.5 mm减小到t=1 m的25.4 mm，减小30.4%。可见前墙厚度对支护结构水平变形的影响十分明显，在设计中合理地选择前墙厚度、在施工中重视施工质量可以明显改善基坑支护效果。随着前墙厚度的减小，作用在后墙的主动土压力明显减小。

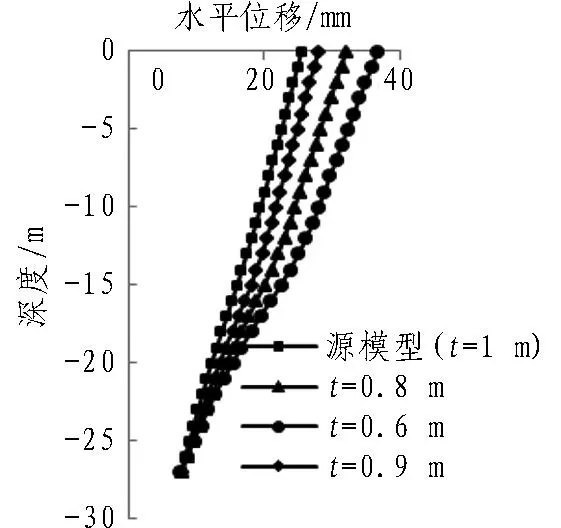
(a) 前墙水平位移的变化规律

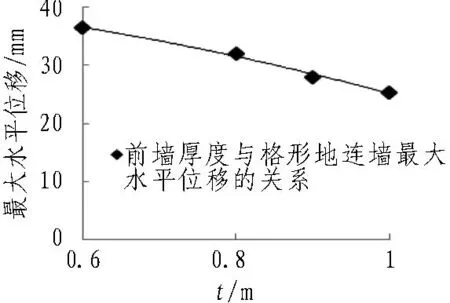
(b) 最大水平位移随t的变化规律

(c) 后墙主动土压力变化规律

Fig.8Effects of width of frontwall on deformation of underground diaphragm wall

4.4内坑被动区加固的影响

在内坑被动区用水泥搅拌桩加固能够改善被动区的土体性质，被动区加固体按弹性体考虑，加固区土体弹性模量E分别取40、60、80、100 MPa。图9表示内坑被动区5.5 m深度范围内土体用水泥搅拌桩加固后支护结构的变形和土压力变化情况，由图9可以看出，内坑加固对墙体水平变形产生较大影响，随着加固土体的弹性模量增大，墙体水平位移不断减小，最大水平位移由E=20 MPa时的25.4 mm减小到E=100 MPa时的19.9 mm。由图9(b)可知，随着被动区土体弹性模量的增大，墙身侧向变形进一步减小，但幅度趋向缓和，因此在实际工程中为达到较高的性价比，宜通过计算来选择确定加固区深度和程度[13-15]。随着内坑的加固，作用在后墙下部区域的主动土压力明显增大，说明后墙下部土体对后墙嵌固作用的加强，有助于开挖时保持整个支护结构的稳定，这与文献[3]研究所得规律吻合，且土体弹性模量E取不同值时相互之间的土压力变化较小。

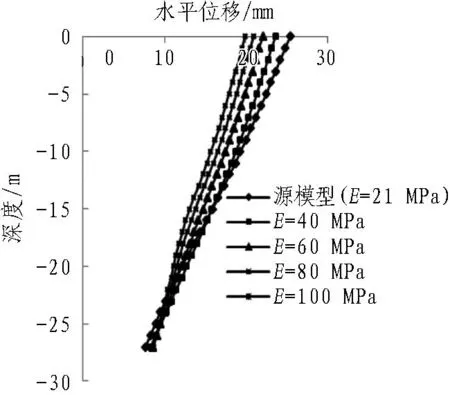
(a) 前墙水平位移的变化规律

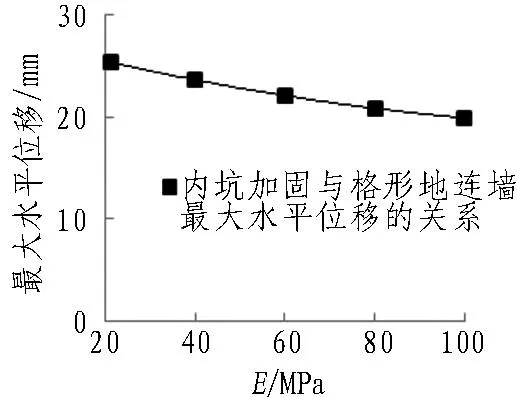
(b) 最大水平位移随弹性模量E的变化规律

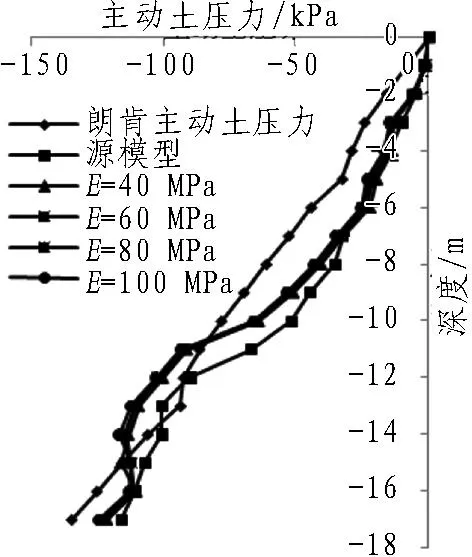
(c) 后墙主动土压力变化规律

Fig.9Effects of width of reinforcement of foundation pit on deformation of underground diaphragm wall

5结论与讨论

本文以南京某基坑工程的格形地连墙支护结构为背景，利用有限元方法建立三维模型，研究此类支护结构基坑工程的变形和受力特征，并对格形地连墙的几何尺寸(后墙和隔墙深度、后墙宽度、前墙厚度)、内坑加固等因素进行分析探讨，研究表明：

2)随着工况的展开，前、后墙主动土压力随着开挖深度的增加而不断减小，其数值均小于静止土压力，但前、后墙的被动土压力随着开挖深度的增加而不断增大，且均大于静止土压力。

3)减小后墙和隔墙深度h在墙顶下1/6墙体深度内墙体水平位移略有增大，1/6～1/2墙深范围内墙体水平位移变化较大，说明增大h对减小基坑土体位移有一定作用。

4)减小前墙厚度对支护结构水平变形的影响十分明显，且作用在后墙的主动土压力明显减小。

5)后墙宽度的增加，可以减小支护结构水平变形，但其作用效果却在不断降低。

6)随着被动区土体弹性模量的增大，墙身侧向变形明显减小，作用在后墙下部区域的主动土压力明显增大，且不同土体弹性模量E之间的土压力变化不大。

本文在研究过程中未能考虑时间因素的影响，特别是对于格型地连墙这种自立式支护结构，开挖过程中暴露的时间对基坑变形影响较大，后续研究可以考虑时间因素对以格型地连墙为支护结构的深基坑受力变形的影响。

参考文献(References):

[1]侯永茂.软土地层中格形地下连续墙围护结构性状研究[D].上海:上海交通大学,2010.(HOU Yongmao.Behavior of cellular diaphragm wall in soft deposit[D].Shanghai:Shanghai Jiaotong University,2010.(in Chinese))

[2]建筑基坑支护技术规程：JGJ 120—2012[S].北京:中国建筑工业出版社,2012.(Technical specification for retaining and protection of building foundation excavations:JGJ 120—2012[S].Beijing:China Architecture &Building Press,2012.(in Chinese))

[3]仇建春,时爱祥,夏友超,等.双排格形地下连续墙的空间变形三维有限元分析[J].水利水电技术,2014,45(8)：78-82.(QIU Jianchun,SHI Aixiang,XIA Youchao,et al.3-D finite element analysis on spatial deformation of double-row cellular continuous diaphragm wall[J].Water Resources and Hydropower Engineering,2014,45(8):78-82.(in Chinese))

[4]周广柱,徐伟,陈宇.格形地连墙与软土相互作用的离心试验研究[J].岩土力学,2011,32(增刊1):134-140,252.(ZHOU Wenzhu,XU Wei,CHEN Yu.Centrifugal model test study of interaction of gridding concrete retaining wall and soft soil[J].Rock and Soil Mechanics,2011,32(S1):134-140,252.(in Chinese))

[5]梅英宝.自立式格形地下连续墙围护基坑变形实测分析[J].岩土工程学报,2010,32(增刊1):463-467.(MEI Yingbao.Measured deformation of self-supporting lattice concrete diaphragm walls[J].Chinese Journal of Geotechnical Engineering,2010,32(S1):463-467.(in Chinese))

[6]夏建国.格形地连墙结构的设计与施工方案探讨[J].水运工程,2004(11):88-91.(XIA Jianguo.Design and construction schemes of cellular diaphragm wall[J].Port &Waterway Engineering,2004(11):88-91.(in Chinese))

[7]时爱祥,邓祥吉,仇建春,等.格形地连墙的三维有限元分析[J].南水北调与水利科技,2015,13(3):571-574.(SHI Aixiang,DENG Xiangji,QIU Jianchun,et al.Three-dimensional finite element analysis of cellular diaphragm wall[J].South-to-North Water Transfers and Water Science &Technology,2015,13(3):571-574.(in Chinese))

[8]梁穑稼,徐伟，陈宇.格形地下连续墙基坑施工阶段侧向变形[J].西南交通大学学报,2015,50(1):150-155,172.(LIANG Sejia,XU Wei,CHEN Yu.Lateral deformation of cellular diaphragm wall at excavation stage[J].Journal of Southwest Jiaotong University,2015,50(1):150-155,172.(in Chinese))

[9]杨永文.杭州软土地区排桩墙与T型地连墙深基坑变形性状研究[D].杭州:浙江大学,2012.(YANG Yongwen.Study of characteristics of deep excavation utilizing pile wall and T-diaghram wall in Hangzhou soft clays[D].Hangzhou：Zhejiang University,2012.(in Chinese))

[10]刘燕,刘国彬,孙晓玲,等.考虑时空效应的软土地区深基坑变形分析[J].岩土工程学报,2006,28(增刊):1433 -1436.(LIU Yan,LIU Guobin,SUN Xiaoling,et al.Analysis of deformation laws by using the rule of time-space effect in soft soil excavation[J].Chinese Journal of Geotechnical Engineering,2006,28(S):1433-1436.(in Chinese))

[11]胡曦刚.倒“T”型变截面地下连续墙在基坑支护工程中的应用[J].土工基础,2004,18(6):29-31.(HU Xigang.Application of the type of “Inverted T” diaphragm in foundation pit of a mansion[J].Soil Engineering and Foundation,2004,18(6):29-31.(in Chinese))

[12]何良德,杨艺平,胡家顺,等.T型桩基地连墙组合式码头结构受力特性研究[J].水道港口,2012,33(6):523-531.(HE Liangde,YANG Yiping,HU Jiashun,et al.Research on stress characteristic of wharf structure combined with T-section pile and diaphragm wall[J].Journal of Waterway and Harbor,2012,33(6):523-531.(in Chinese))

[13]罗战友,刘薇，夏建中.基坑内土体加固对围护结构变形的影响分析[J].岩土工程学报,2006,28(增刊):1538-1540.(LUO Zhanyou,LIU Wei,XIA Jianzhong.Effect of improvement soils on lateral deformation of foundation pits[J].Chinese Journal of Geotechnical Engineering,2006,28(S):1538-1540.(in Chinese))

[14]刘建航,侯学渊.基坑工程手册[M].北京:中国建筑工业出版社,1997:2-30.(LIU Jianhang,HOU Xueyuan.Excavation engineering manual[M].Beijing:China Architecture &Building Press,1997:2-30.(in Chinese))

[15]俞建霖,龚晓南.基坑工程变形性状研究[J].土木工程学报,2002,35(4):86-90.(YU Jianlin,GONG Xiaonan.Research on deformation of foundation-pit engineering[J].China Civil Engineering Journal,2002,35(4):86-90.(in Chinese))

Study of Soil Stress and Deformation of Support Structure of Gridding Underground Diaphragm Wall of Deep Foundation Pits

WANG Fei1,LIU Yawen1,SU Jingbo2,FENG Bin3,JIA Shun3,LIANG Jinjun1

(1.School of Field Engineering,PLA University of Science and Technology,Nanjing 210007,Jiangsu,China;2.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,Jiangsu,China;3.Nanjing Major Road and Bridge Construction Headquarters,Nanjing 210000,Jiangsu,China)

Abstract:The finite element model of support structure gridding underground diaphragm wall of a deep foundation pit in Nanjing is established;and Mohr-Coulomb elastoplastic constitutive model is adopted for rocks and soils.The finite element method is used to analyze the deformation of the deep foundation pit and the distribution rules of soil stress;and the results are compared with measured data and Rankine soil stress.The influencing factors,i.e.depth of backwall and separating wall,width of backwall,thickness of frontwall and foundation reinforcement,are analyzed.The analytical results show that:1) The lateral deformation of gridding underground diaphragm wall is similar to that of cantilever beam.2) The lateral deformation of wall roof is the largest,which shows that the deformation rules of the above-mentioned underground diaphragm wall are different from that of conventional multiple-supported structure.3) The influencing factors of thickness of frontwall and reinforcement of foundation pit are obvious.

Keywords:deep foundation pit;gridding underground diaphragm wall;finite element analysis;deformation;soil stress

收稿日期：2015-12-15;修回日期:2016-02-03

基金项目：南京重大路桥建设指挥部科学研究项目(编号20140212)

第一作者简介：王飞(1991—)，男，安徽合肥人，解放军理工大学桥梁与隧道工程专业在读硕士，研究方向为基坑工程。E-mail：wfeihome@126.com。

DOI:10.3973/j.issn.1672-741X.2016.06.011

中图分类号：U 45

文献标志码：A

文章编号：1672-741X(2016)06-0721-07