轮毂驱动电动汽车悬架创新设计与优化

聂高法,时培成,孙阳敏,彭闪闪,张 军

(安徽工程大学机械与汽车工程学院,安徽芜湖 241000)



轮毂驱动电动汽车悬架创新设计与优化

聂高法,时培成∗,孙阳敏,彭闪闪,张 军

(安徽工程大学机械与汽车工程学院,安徽芜湖 241000)

摘要:为了改善轮毂驱动电动汽车悬架垂向振动特性,建立轮毂驱动电动汽车1/4车辆动力学模型,在Matlab/Simulink中进行仿真分析．首先,对比原车悬架,研究轮毂电机转矩波动对车辆垂向振动特性的影响．其次,将轮毂电机利用弹簧阻尼器与轮毂弹性连接,使轮毂电机变成类簧载质量,并优化悬架参数．最后,对优化前后的1/4车辆动力学模型进行对比分析．仿真表明,优化后的悬架系统使得车身垂向振动特性优于电机与轮毂刚性连接的悬架,研究结果为改善轮毂电机电动汽车垂向振动特性提供了依据．

关 键 词:电动汽车;轮毂电机;悬架;优化

轮毂电机驱动形式被业界称为电动车辆终极驱动形式,由于其四轮驱动力矩独立可控、转矩转速易于测得,因此,在稳定性、主动安全控制和节能方面相比于现有传统电动汽车(只有一个集中大电机驱动方式)具有显著的优势,也是研究新一代车辆控制技术、探索车辆动力学性能的理想载体,已成为世界各大汽车公司和科研院所的研究热点[1-2]．

但轮毂驱动在实际应用中还存在诸多挑战:第一,轮毂电机与轮毂结合增加了车辆非簧载质量,恶化了车辆行驶平顺性和安全性;第二,因电机直接或经过减速机构与车轮固连,易受路面激励而产生较大振动,既可能加剧定子与转子间的磁隙波动,也将缩短电机结构的工作寿命;第三,因省去传统内燃机驱动车辆的传动系统,电机力矩波动直接作用于车轮,可能引起悬架前后方向共振以及整个驱动系统的振动问题．因此,开展轮毂驱动电动汽车垂向振动机理及抑制方法研究具有重要意义,相关研究成果将为轮毂驱动电动汽车的开发提供设计理论与方法[3-4]．

采用低速外转子轮毂电机,建立轮毂电机驱动电动车1/4车辆动力学模型,在Matlab/Simulink中进行仿真,分析轮毂电机转矩波动对簧载质量垂向振动的影响,创新设计轮毂电机减振系统并进行参数优化,以改善轮毂电机转矩波动对车辆平顺性的影响．

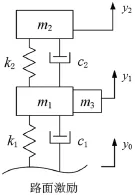
图1 轮毂驱动汽车1/4车辆垂向振动模型

1 轮毂驱动汽车垂向动力学模型

1．1 1/4车辆垂向振动模型的建立

轮毂驱动汽车动力学模型由车辆悬架模型和轮毂电机转矩输入两部分组成．经过简化的含有轮毂电机的1/4车辆垂向振动模型如图1所示．由图1可知,m1为非簧载质量(不含轮毂电机质量);m2为簧载质量;m3为轮毂电机质量;k1、c1为轮胎刚度和阻尼;k2、c2为车辆悬架刚度和阻尼;y0、y1和y2为路面不平度、车轮和车身的位移;Ft为轮胎接地力的波动量;Fn为簧载质量的振动输入．依据图1,车辆垂向振动动力学方程为:

车辆垂向振动模型参数初步选取数值如表1所示．

表1 1/4车辆垂向振动模型参数

1．2 轮毂电机转矩波动动力学模型

采用永磁同步电机作为驱动单元,考虑电流传感器的直流偏移误差．

在ABC坐标系中,电机三相电流方程式为:

在正弦分布电机磁场下,电磁转矩表达式为:

电机转矩波动为:

1．3 路面随机输入仿真模型

国际道路不平度试验中规定,沿着车辆的行驶方向,路面不平度定义为行驶道路表面相对于理想平面的偏离[5]．路面功率谱密度函数能够表示路面不平度能量在空间频域的分布,其拟合表达式为:

式中,n为空间频率(m－1),是波长λ的倒数;n0为参考空间频率,n0＝0．1 m－1;Gq(n0)为参考空间频率n0下的路面功率谱密度,称为路面不平度系数,其值取决于道路的路面等级;W为频率指数,为双对数坐标上斜线的频率,它决定路面功率谱密度的频率结构．

路面一般分为8个等级．在8个等级中,B级路面更接近现实路面,故选择B级路面作为测试路面,根据式(8)在Simulink中建立B级路面谱仿真模型如图2所示．

2 悬架垂向振动仿真

2．1 轮毂电机转矩波动输入下的仿真分析

根据式(7)在Matlab中建立轮毂电机转矩波动模型进行仿真,设直流偏移误差4A．得到电机转矩波动时域特性如图3所示．

以轮毂驱动电动汽车1/4车辆动力学模型为研究对象,采用表1参数,在轮毂电机转矩波动输入下对系统进行激振仿真,探究由于轮毂电机的引入对悬架垂向振动造成的影响,仿真结果如图4所示．

非簧载质量为45 kg(m1＋m3)时,悬架在B级路面随机波和轮毂电机转矩波动双重激励下车身垂向振动加速度¨y2的功率谱密度对比图如图4所示．由图4可知,在轮毂电机转矩波动影响下,车身垂向振动加速度¨y2在9～18 Hz明显增大,峰值从49 m2/s3上升到61 m2/s3,幅值在9 Hz左右的峰值增加将近24．5%．综上所述,轮毂电机转矩波动对车辆的垂向振动有较大影响,必须采取改进悬架结构或者优化参数,以改善轮毂驱动电动汽车的平顺性．

图2 B级路面谱Simulink仿真模型

图3 轮毂电机转矩波动时域特性

图4 车身垂向振动加速度¨y2功率谱

2．2 改进的含有轮毂电机的1/4车辆垂向振动模型

在电机与车轮和车身之间加入弹簧阻尼减振系统,得到的1/4车辆垂向振动模型如图5所示．其动力学方程为:

图5 改进的轮毂电机驱动1/4车辆垂向振动模型

由图5可知,m1为非簧载质量(不含轮毂电机质量);m2为簧载质量;m3为轮毂电机质量;k1、c1为轮胎刚度和阻尼;k2、c2为车辆悬架刚度和阻尼;y0、y1和y2分别为路面不平度、车轮和车身的位移;y4为电机位移;k3、c3为电机与车身间弹簧阻尼减振系统的弹簧刚度和阻尼系数;c4、k4为电机与车轮间弹簧阻尼减振系统的弹簧刚度和阻尼系数．

2．3 悬架参数优化

以车身垂向振动加速度、悬架动挠度和车轮动载荷这3个指标的均方根之和为优化目标[6],具体的目标函数为:

其中,车身垂向振动加速度的均方根值表达式为:

悬架动挠度的均方根表达式为:

车轮相对动载荷的均方根表达式为:

式中,Gq(n0)为路面谱均值,单位是m3;u是车辆速度,单位是m/s．

车辆垂向振动模型参数的初值如表2所示．选取电机与车轮和车身之间弹簧阻尼减振系统的弹性刚度K3、K4,阻尼系数C3、C4为优化变量[7-8]．考虑实际情况,选用17英寸的轮毂,由于将轮毂电机和制动系统集成在轮毂上,对电机大小和安装位置需要较高的尺寸要求．若电机外径为350 mm,电机与车轮的相对位移限定在10 mm内,则约束条件为σy3－y1≤0．00 316 mm．

在Matlab中编写程序,利用优化工具patternsearch函数对上述模型进行仿真,优化结果如表3所示．由表3可知,优化后的轮毂电机减振系统为电机与车轮之间保留弹簧阻尼减振系统,轮毂电机与车身之间不设减振单元．经优化后的轮毂电机驱动1/4车辆垂向振动模型如图6所示．

表2 1/4车辆垂向振动模型参数

表3 车辆垂向振动模型悬架参数优化结果

图6 优化后的轮毂电机驱动1/4车辆垂向振动模型

2．4 轮毂电机悬架优化模型的对比分析

把未安装轮毂电机的车辆垂向振动模型设为构型1,将电机与车轮直接刚性连接的振动模型设为构型2,将优化改进的轮毂电机驱动1/4车辆垂向振动模型设为构型3．分别对车轮相对动载荷、车身悬架动挠度和车身垂向振动加速度¨y2对B级路面激励的传递特性进行仿真,对比结果如图7、图8和图9所示．

由图7和图8仿真结果可知,加入轮毂电机的振动模型2的车轮相对动载荷和车身悬架动挠度均大于原始车辆悬架的振动模型1,使振动峰值大幅增加,且振动峰值频率从13～14 Hz降低到7～8 Hz．经过改进优化的振动模型3与电机和车轮直接刚性连接的振动模型2相比,车轮相对动载荷、车身悬架动挠度均明显降低了．

由图9仿真结果可知,对比常规车辆悬架的构型1与电机与车轮直接刚性连接的振动构型2可以看出,轮毂电机与轮毂的刚性连接增加了悬架非簧载质量,振动幅值大幅增加．在7 Hz左右,地面激励对车身振动的传递明显增大．通过对悬架参数的优化,由经过改进优化的振动构型3可以看出,将轮毂电机质量转化为类簧上质量后, 在7 Hz左右的幅值显著下降,并且在4～30 Hz之间的幅值均小于模型1和模型2．由此可见,改进的悬架构型使得轮毂电机驱动轮的垂向振动特性优于电机与轮毂刚性连接的悬架振动特性,并且在超过7 Hz的频率区域内比无电机的原车辆悬架垂向振动幅值更小,明显改善了车辆的平顺性．

图7 车轮相对动载荷对B级路面激励的传递特性

图8 车身悬架动挠度对B级路面激励的传递特性

图9 车身垂向振动加速度对B级路面激励的传递特性

3 结论

对车辆1/4悬架振动模型进行仿真,分析轮毂电机转矩波动对汽车平顺性的影响．仿真结果表明,轮毂电机转矩波动对车身垂向振动加速度¨y2功率谱密度有明显影响．在轮毂电机转矩波动影响下,车身垂向振动加速度¨y2在9～18 Hz明显增大,幅值在9 Hz左右的峰值增加将近24．5%．改进设计的轮毂电机车辆悬架结构,在轮毂电机与车轮和车身之间加入弹簧阻尼减振器,将轮毂电机的非簧载质量转化为类簧载质量,并优化轮毂电机弹簧减振系统参数,使得车辆悬架系统在大于7 Hz的频率区域内的振动幅值都明显降低,能改善车辆的行驶平顺性．

参考文献:

[1] 余卓平,冯源,熊璐．分布式驱动电动汽车动力学控制发展现状综述[J]．机械工程学报,2013,8:105-114．

[2] 童炜,侯之超．轮毂驱动电动汽车垂向特性与电机振动分析[J]．汽车工程,2014,4:398-403,425．

[3] 李程祎,左曙光,段向雷．考虑转矩波动的电动汽车悬架NVH性能参数优化[J]．汽车工程,2013,4:303-306,316．

[4] 莫旭辉,赵宇航,钟志华,等．基于6σ稳健性方法的汽车行驶平顺性优化[J]．中南大学学报:自然科学版,2012,11: 4 286-4 292．

[5] 马英,邓兆祥,谢丹．轮毂电机悬架构型分析与优化[J]．中南大学学报:自然科学版,2014,9:3 008-3 014．

[6] K Nam,H Fujimoto,Y Hori．Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors[J]．IEEE Transaction on Vehicular Technology,2012,61(5):1 972-1 985．

[7] 罗玉涛,谭迪．一种带新型内置悬置系统的电动轮结构研究[J]．汽车工程,2013,12:1 105-1 110．

[8] 林程,王刚,曹万科,等．基于LO-EKF算法的分布驱动电动汽车状态估计的研究[J]．汽车工程,2014,36(11):1 316-1 320．

Innovative design and optimization of suspension of in-wheel-motor-driven electric vehicles

NIE Gao-fa,SHI Pei-cheng∗,SUN Yang-min,PENG Shan-shan,ZHANG Jun
(College of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu 241000,China)

Abstract:To improve vertical performance of suspension of in-wheel-motor-driven electric vehicle,a quarter-car dynamic model of a electric vehicle drived by in-wheel motor was established and simulated in Matlab/Simulink．First,compared with the original vehicle＇s suspension,the effect of torque ripple to performance of vertical vibration of in-wheel motor was studied．Second,with in-wheel motor connected, by wheel hub elastically(using spring-damper)and turned into similar sprung mass,the suspension parameters were optimized．Finally,the quarter-car dynamic model before-and-after optimization was compared．The simulation results showed that the suspension after optimization was superior to the suspension with rigid connection between the motor and wheel hub in performance of vertical vibration．The results provided the basis for improving performance of vertical vibration of the in-wheel-motor-driven electric vehicle．

Key words:electric vehicle;in-wheel motor;suspension;optimization

中图分类号:U461．4

文献标识码:A

收稿日期:2015-11-03

基金项目:国家自然科学基金资助项目(51575001)

作者简介:聂高法(1988-),男,安徽阜阳人,硕士研究生．

通讯作者:时培成(1976-),男,安徽六安人,教授,博士．