用向量法解决立体几何中的探索性问题
北京市延庆第一中学 付冬雪
用向量法解决立体几何中的探索性问题
北京市延庆第一中学付冬雪

在直角坐标系中引入空间向量,为解决立体几何问题提供了一个有效的代数工具.
立体几何中的探索性问题一般描述的是动态过程,需要一定的空间想象能力,而向量可以使复杂的问题简单化,降低思维难度,可操作性强,能有效提高数学学习效率.
下面列举几种常见的用向量法解决立体几何中探索性问题的类型与方法.
一、与平行有关的探索性问题
问题1:如图1,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.若SD⊥平面PAC,问:侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求线段CE:ES的值.若不存在,说明理由.
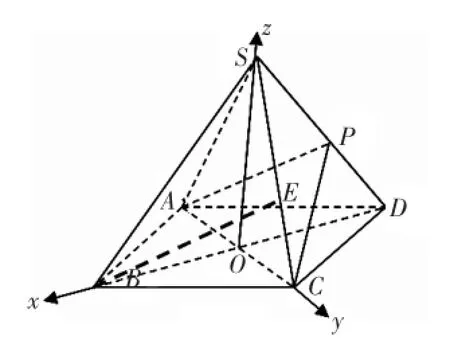
图1
假设在侧棱SC上存在一点E使BE∥平面PAC.连BD,设AC交于BD于O,由题意知,SO⊥平面ABCD,以O为原点建立如图1所示的空间直角坐标系O-xyz,设OB=1,则B(1,0,0),D(-1,0,0),S(0,0,),C(0,1,0).
因为BE不在平面PAC内,故BE∥平面PAC.
二、与垂直有关的探索性问题
问题2:如图2,四边形ABCD是边长为1的正方形,MD⊥面ABCD,NB⊥面ABCD,且MD=NB=1,E为BC中点,问:在线段AN上是否存在一点S,使ES⊥平面AMN?若存在,求线段AS的长;若不存在,说明理由.
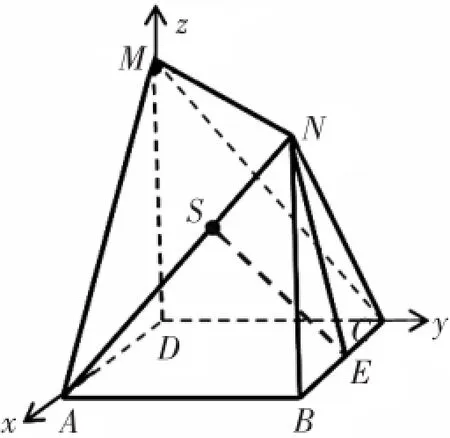
图2
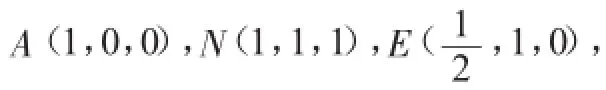
点评:空间中的线线、线面、面面垂直都可转化为两向量的垂直来解决,本问题也可以利用向量与平面AMN的一个法向量共线来求得S的位置.
三、与角有关的探索性问题
问题3:已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.问:线段PD上是否存在一个动点M,使得直线GM与平面EFG所成角为,若存在,求线段PM的长度,若不存在,说明理由.
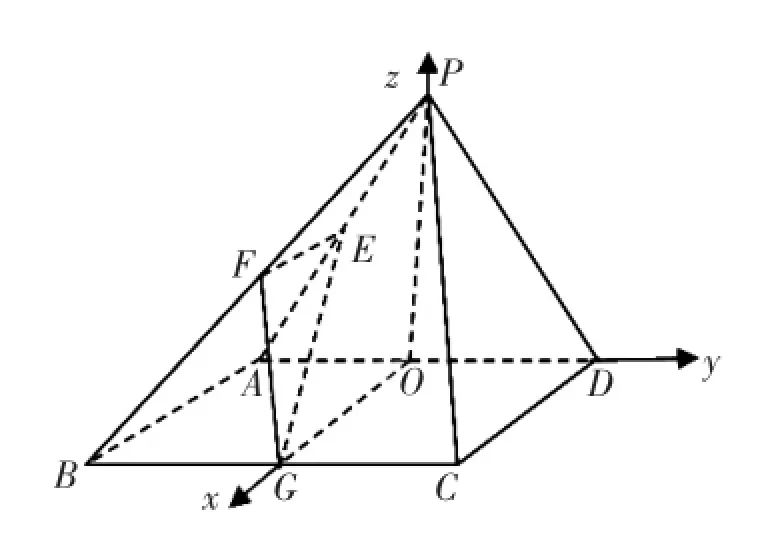
图3
解析:取AD中点O,连结PO
∵平面PAD⊥平面ABCD,PO⊥AD,∴PO⊥平面ABCD
如图3,以O点为原点,建立空间直角坐标系O-xyz,则O(0,0,0),A(0,-2,0),B(4,-2,0),C(4,2,0),D(0,2,0),
从以上问题可以看出,向量是“数”与“形”相互转化的桥梁和纽带,既能体现“数”的运算性质,又具有“形”的直观特征,能融数形于一体.因此,向量是解决立体几何中平行、垂直、角和距离的有效工具.用向量法解决立体几何中的探索性问题时,要恰当地建立空间直角坐标系,合理地等价转化所求问题,就能将几何问题代数化,将复杂问题简单化,将逻辑推理运算化.
编辑/王一鸣
E-mail:51213148@qq.com

