基于大字典的LZW压缩算法的降熵改进

陆振龙　张　箐

1(中国科学院遥感与数字地球研究所　北京 100094)2(中国科学院大学　北京 100094)



基于大字典的LZW压缩算法的降熵改进

陆振龙1,2张箐1*

1(中国科学院遥感与数字地球研究所北京 100094)2(中国科学院大学北京 100094)

摘要在分析压缩算法LZW的基础上，针对LZW算法在字典规模增大时出现的压缩后数据平均信息熵快速增大的不足，提出一种改进的压缩算法。利用数据中普遍存在的空间相关性，在保存大字典的同时缩小每次压缩实际使用的字典范围，以此减小压缩后数据的信息熵。给出改进算法与LZW压缩算法的性能对比，实验结果表明改进算法在减小压缩后数据的信息熵方面取得了2%～16.9%的优化。

关键词数据压缩算法信息熵数据相关性

0引言

遥感技术增强了人类观察和探索世界的能力，扩展了人类可以观测的范围，缩短了观察宏观现象所需的时间，同时使得因自然条件恶劣无法实地观察的环境也能用遥感技术得以观察。人以眼睛进行观察活动时，可以快速处理观察到的图像并作出响应。应用遥感技术时，若能提高快速响应能力，将大大增强遥感技术的效果。但是，提高系统响应速度的一个巨大挑战来源于在带宽一定的条件下不断增大的遥感数据量和远距离的传输。数据压缩技术在发送端通过去除数据冗余而减少实际传输的数据量，从而缩短了数据传输时间。

基于字典的数据压缩算法在许多应用领域取得了良好的压缩效果。文献[1]提出的TCP自适应压缩传输方案中自适应压缩器采用基于字典的压缩方法与Huffman编码相结合的压缩编码方案。文献[2]对三大类共10种压缩的全文自索引方法进行了分析和比较，基于字典的LZ压缩算法的全文自索引算法在索引建立、定位和提取几个方面有明显的优势。

基于字典的数据压缩算法是一类无损压缩算法，其基本思想是，在数据中普遍存在着结构冗余，数据中的某些“词组”会重复出现。因此，基于字典的压缩算法使用滑动窗口或者显式的字典，用于存储已经压缩的数据中可能会在将来重复出现的“词组”，当发现再次出现的词组时，就发送字典的索引代表词组本身。当用于表示字典索引的数据量少于表示词组所需的数据量时，能够取得好的压缩效果。在基于字典的数据压缩算法中，字典容量大小与压缩效果有着密切的联系。本文对此进行研究，并提出了改进方法。

1基于字典的压缩算法LZW及相关改进算法分析

1.1应用LZW算法的数据压缩系统介绍

应用LZW算法[3]的压缩系统的编码过程一般可以用图1所示。

图1应用LZW的压缩系统编码流程

LZW

压缩部分(即Ⅰ过程)在编码端完成两项工作：其一是在字典中查找当前的词组是否存在。如果存在，则继续查找是否存在更长的词组；否则，用对应字典索引替代当前词组作为编码输出。其二是将当前字典不存在的词组作为新词组加入字典，完成字典的更新。传统

LZW

算法每次形成并加入长度增加一个符号的新词组；

LZMW

[4]

和

LZAP

等算法

[5]

在如何形成新词组方面做出改进，改进算法使字典适应输入数据的速度加快。

1.2应用LZW的压缩系统前后数据特性分析

如图1所示，应用LZW算法的压缩系统有过程Ⅰ和过程Ⅱ两个处理阶段。过程Ⅰ将值域为[Pmin,Pmax]的待压缩数据X处理形成值域为[Vmax-1]的数据Y，其中Vmax是LZW的字典容量大小。例如，用8bit表示一个像素点的灰度图像使用字典容量为216的LZW算法经过程Ⅰ处理，是将值域为[0,28-1]的数据流X处理形成值域为[0,216-1]的数据流Y。

过程Ⅱ将数据流Y用信道符号集{α1,α2,…,αr}编码成适应信道传递的符号流Z。例如，二元离散信道符号集为{0,1}，即α1=0，α2=1。则过程Ⅱ将值域为[0,216-1]的数据流Y按照单一可译的原则编码成{0,1}的比特流。

(1)

其中，H(S)表示信源信息熵，即数据流Y的信息熵，r表示信道符号种类。这里以符号集为{0,1}的信道为例，因此上式改写为：

(2)

对于单一可译码平均码长的下界，可以通过扩展信源或采用优秀的编码算法如Huffman，算术编码的方式使平均码长接近这个下界[6]。Gzip压缩软件的一个核心部分就是LZ压缩算法与Huffman编码的组合。因此，本文用数据流Y(经过程Ⅰ处理后的数据)的信息熵作为衡量指标来比较在待压缩数据源X相同的情况下，过程Ⅰ使用不同的压缩算法产生的数据流Y可以达到的最短平均码长。

1.3LZW改进算法分析

DTLZW算法[8]提出传统LZW是基于平稳遍历信源的假设，但是实际信源多为局部平稳。因此提出双串表，也可以看作是双字典的改进算法，利用信源是局部平稳的特点，在当前字典不能很好符合当前局部时(表现为在当前串表中找到匹配的概率降低)，快速切换至另一个串表，从而保证压缩效率能维持在较高的水平上。

LZSWH算法[9]利用LZ77和LZ78两类压缩算法对于不同类型的数据压缩性能不同，将这两类算法的代表LZSS和LZW结合，并加入了H参数，控制LZSWH向LZSS和LZW的偏向程度，得到了对于不同类型数据比单一算法更好的适应性。

文献[10]提出一种综合了LZW远距离记忆性好和LZSS对于信源特性的快速适应特性优点的压缩算法，每轮压缩均先后使用LZW与LZSS进行编码，并采用能搜索到更长匹配的编码方式进行输出，同时用1bit来标示采用的编码方式是LZW还是LZSS。另外因为小序号字典项输出时占用bit数少，但是常常被命中率低的字典项占用，提出将命中率低的字典项，主要是生成较长的字典项过程中产生的中间字典项，逆序加入字典，分配较大的字典序号，从而提高小序号字典项的命中率，增加了压缩效率。

LZC算法将字典的初始容量预设得较小，因此初始阶段，Y的平均码长将比较小。当字典装满时，将字典容量动态增长为2倍，此时生成数据Y的平均码长也增加1。如此重复，直至字典的大小达到预设的最大容量。LZC对字典采用动态增长的手段，降低了Y数据流的平均码长。例如，最大字典容量为216的LZW和LZC算法，LZW产生的数据流Y采用定长编码的平均码长为16bit，LZC字典中项数少于初始容量512项时，产生的数据平均码长为9bit；当字典逐渐装满，达到512项时，字典容量增长为2倍，产生数据的平均码长为10bit；如此重复，直至字典达到216项，产生数据的平均码长为16bit。因此LZC产生的数据Y的平均码长短于LZW产生的数据的平均码长。

LZT算法的一个特点是对数据流Y用phased-in码[11]进行编码，这将节约开始阶段的bit数，降低平均码长，但随着字典的装满，这部分的作用将逐渐变小。

通过实验结果分析，如表1所示，LZW或现有的各改进算法在字典容量增大时都会出现对数据流Y进行过程Ⅱ编码时平均码长快速增大的现象，这是不利于使用LZW的压缩系统的压缩效果的。字典容量越大，数据流Y的信息熵越大，使平均码长的下限越长。

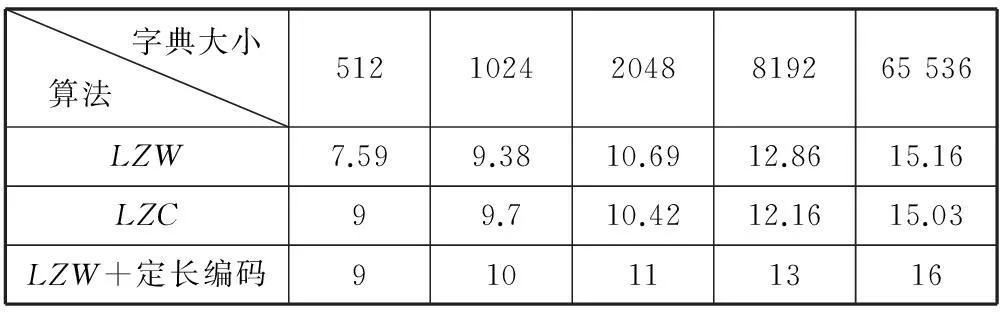
表1　不同字典大小的LZW及其改进算法产生的数据Y的

但同时也不能过度限制字典容量的大小，因为大字典可以保存更多的词组，从而能找到更多的匹配，有利于压缩。因此，需要在保持大字典容量的情况下，在降低数据流Y的信息熵方面改进，以取得更低的平均码长。

2改进算法的提出

LZW算法的大字典容量能保存更多词组，找到更多的匹配，所以，需要在保持大字典容量的前提下降低经过程Ⅰ处理的数据流Y的信息熵。

对不同图像进行观察，发现图像内部普遍存在空间周期性，即某个图像特征往往会重复出现，如图2所示。图3所示为某图像按行扫描后的像素曲线图，图中B段图像曲线与已经发生的A段曲线极为相似，说明这两段图像代表相似的图像模式。若B中当前的一个词组在A中F处找到匹配，说明当前区域B与区域A中有一部分特征相同，则B与A将以高概率属于相似的图像模式，即B中下一个词组也将以高概率落在这个图像模式中。因此在每次找到较长的字典项匹配后，我们可以记录下此次匹配的位置，即区域A中的F处，下轮搜索时就在F处的附近进行。

图2　图像的空间周期性

图3　图像像素曲线图

因此，本文提出以下改进处理。首先，将字典设计成能够保存图像空间周期性的结构，即空间上相邻的词组在字典中的位置也相邻。为了使字典具有这种性质，在将新词组写入字典时，用下式确定写入字典的位置：

Indexi=[(Index(i-1)+1)MOD(Vmax)]+Vstart

(3)

其中Indexi代表第i个词组加入字典的位置，MOD为模运算，Vmax代表大字典的容量，Vstart代表LZW改进算法中不能被新字典项覆盖的部分，一般用字典的[0,Vstart-1]写入所有可能的单个信源符号，对于用8bit表示一个像素点的灰度图像来说，Vstart为256。式(3)可以简单解释为“循环写入”，例如，对于字典容量为216项的改进字典，若上一项词组位置为4096，则下一项写入位置4097；若上一项位置为65 535，则下一项写入位置256。

这种改进字典中各项的相对位置如实反映了数据中存在的空间相关性。改进算法利用这种保存在字典中的空间相关性做如下操作，在每次搜索及输出之前，结合上次在字典中找到匹配的位置，做出是使用全部字典还是使用局部字典的决定，相应的处理如下：

If(上轮搜索在大字典中F位置找到长度大于2的匹配)

{

本轮搜索时选择F位置前后L范围作为局部字典进行搜索

如果在局部字典中找到匹配，则输出该匹配在局部字典中的相对位置

}

else{

在大字典中搜索

如果在大字典中找到匹配，则输出该匹配在大字典中的位置

}

因此，利用图像中的空间周期性，很多数据都可以在局部字典中找到；而在局部字典中找到的匹配可以用该匹配在局部字典中的相对位置代替匹配在整个大字典中的绝对位置作为输出。如果使用LZW，过程Ⅰ输出匹配在大字典中的绝对位置，因此数据流Y的值域为[0,Vmax-1]。而用本文提出的改进算法，如果上个词组在字典中找到匹配，则输出当前词组在局部字典中的相对位置，相对位置的值域为[0,2L-1]。虽然改进算法编码后产生的数据流Y的值域相同，但分布不同。改进算法将一些分散在字典中各位置的输出集中在一个相对小的范围中，主要成分变为了[0,Vstart+2L]，各成分概率分布更加不均匀，从而降低了数据流Y的信息熵。

综上所述，本文提出的改进算法的流程如图4所示。

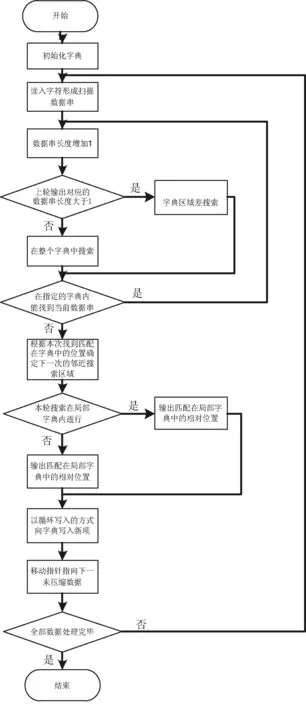
图4　基于大字典的压缩算法LZW降熵改进算法流程图

3改进算法实验

本文首先对一948×450的图像用LZW和本文提出的改进算法分别进行压缩(即图1中的过程Ⅰ)，并对使用不同算法产生的数据流Y中各符号概率分布进行统计，并对出现频数取log得到直方图对比，即图5所示。由图5左侧直方图可以看出，在过程Ⅰ中用LZW处理后产生的数据流Y中各符号近似于均等分布，此时数据流Y的信息熵较大；由右侧直方图看出，若运用本文提出的改进算法，此时数据流Y的分布更加集中，因此信息熵更低。因此，用改进算法更加有利于过程Ⅱ取得更短的平均码长。

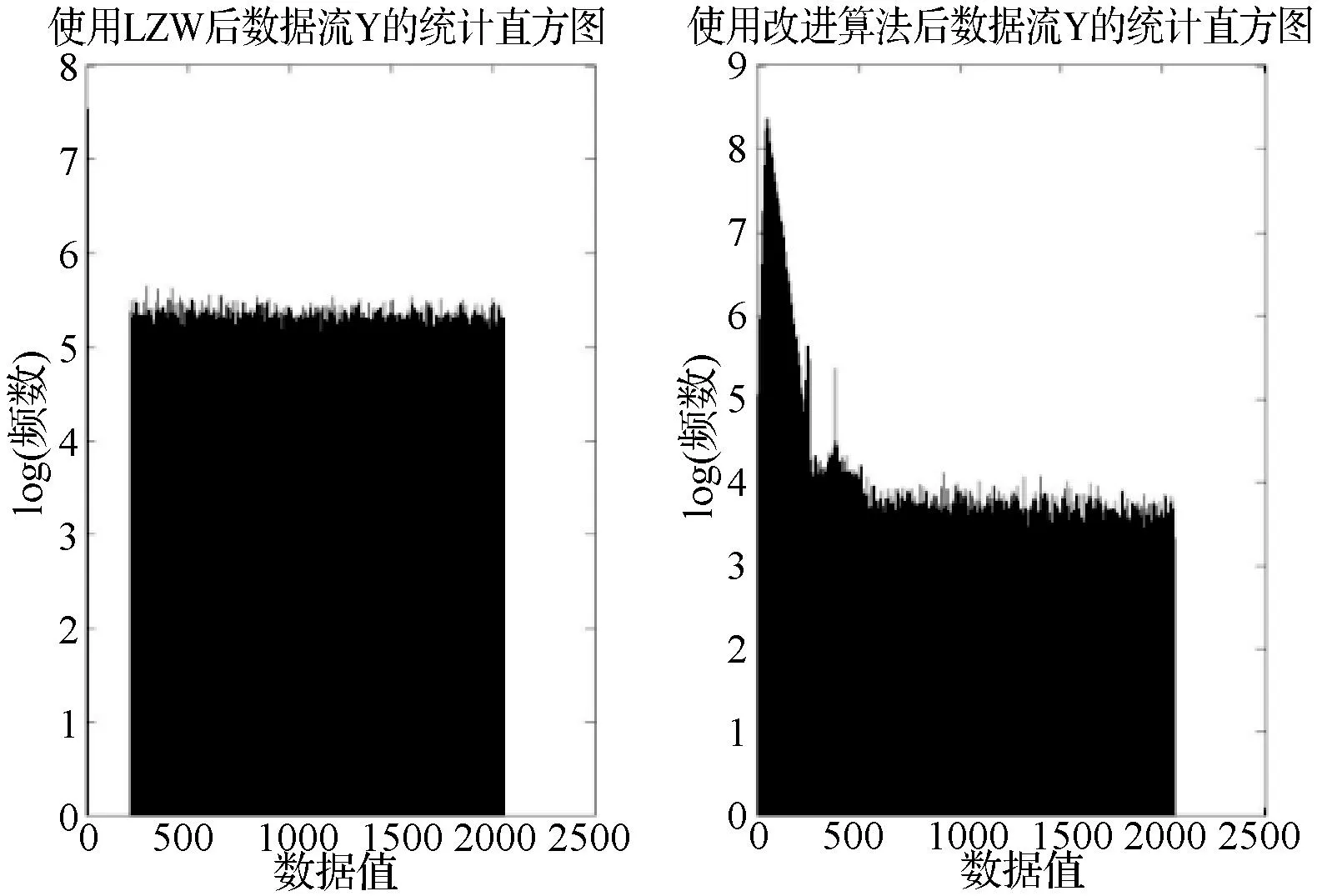
图5　采用LZW和本文改进算法后的数据流各符号概率分布对比

然后对此948×450的图像在图1的过程Ⅰ中采用不同字典容量，不同算法分别进行压缩，并计算产生的数据流Y的信息熵或最短平均码长，得到表2所示。从表2看出，改进算法在不同字典容量都能取得比LZW和LZC更加低的信息熵，在大字典容量时取得的降熵效果更加明显。

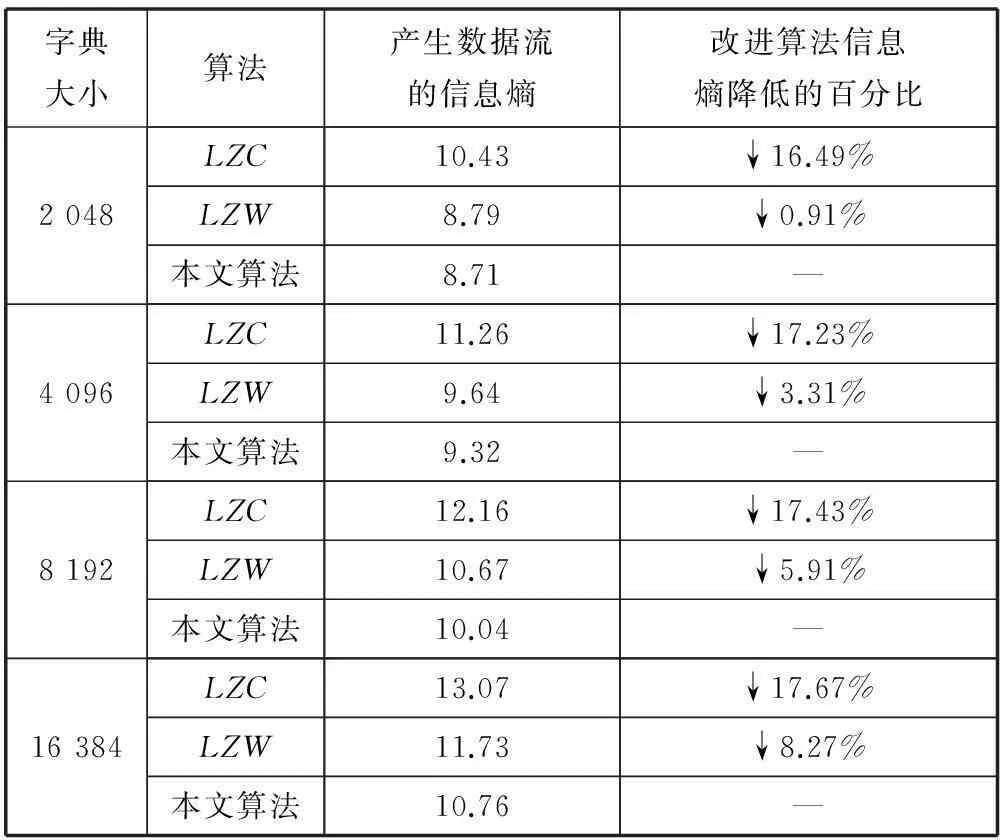
表2　相同数据采用不同字典容量的算法处理后的数据流的信息熵

最后对53幅图像数据分别用相同容量的LZW，LZC和本文实现的改进算法加以压缩，将压缩后数据的平均信息熵进行比较，得到图6所示。改进算法相较采用动态增长字典的LZC取得了7.47%～20.3%的优化；相比LZW与熵编码的组合能取得2%～16.9%的降熵，说明在过程Ⅰ中采用改进算法能取得较好的降熵效果。图6同时说明改进算法较LZW算法能对不同特性的数据取得普遍的降熵效果，说明了本文提出的改进算法的有效性。

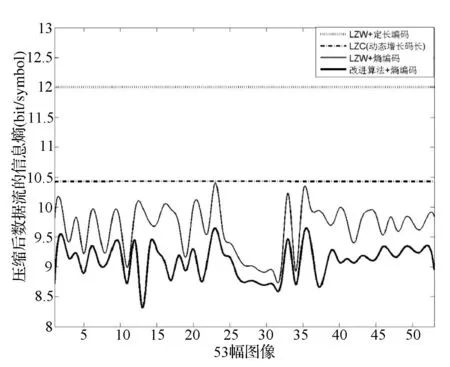
图6　采用LZW和本文改进算法后的数据流信息熵曲线对比

4结语

本文对基于字典的压缩算法LZW进行了研究。研究结果显示：基于大容量字典的LZW压缩算法的相比基于小字典的LZW算法在压缩后数据的平均信息熵方面显著增大，这对于后续进行熵压缩编码不利。通过实验发现，数据中存在普遍的空间周期性，这为提出基于大容量字典的降熵压缩算法提供了可能性。本文使用在大容量字典中自动选取的局部字典进行实际压缩和编码，使压缩后数据流Y中各成分的概率分布更加集中，降低了平均信息熵。经实验验证，改进后的算法在降低压缩后数据的平均信息熵方面取得了2%～16.9%的优化。

今后的研究将集中在以下两个方面，其一，根据本文采用的局部字典选择策略和已有的实验结果，对局部字典选择算法进一步改进，以达到能在选择出的局部字典中以更大概率找到匹配。再配合以本文提出的改进算法本身具有的低平均信息熵特性，从而取得更好的压缩效果。其二，针对本改进算法使用局部字典进行搜索和输出的特性进一步设计字典的数据结构，优化本改进算法的运行效率。同时进一步分析本改进算法产生的数据流的分布特性，为下一步使用其他压缩算法提供先验知识，从而提升工程运用本改进算法的系统整体处理速度。

参考文献

[1] 牟璇,王俊峰,王敏,等.TCP自适应压缩传输方案研究[J].计算机应用与软件,2013,30(11):279-282.

[2] 路炜,刘燕兵,王春露,等.压缩的全文自索引算法研究[J].计算机应用与软件,2014,31(3):11-15,35.

[3]TerryAWelch.ATechniqueforHigh-PerformanceDataCompression[J].IEEEComputer,1984,17(6):8-19.

[4]MillerVSMN.WegmanIEEEInternationalConferenceonDigitalTechnology[C]//SpanningtheUniverse:Communications,1988.Berlin,Springer,1988:131-140.

[5]SalomonDavid,MottaGiovanni.Handbookofdatacompression[M].London:Springer,2010.

[6] 姜丹.信息论与编码[M].安徽:中国科学技术大学出版社,2004.

[7] 吴乐南.数据压缩[M].北京:电子工业出版社,2012.

[8] 吴宇新,余松煜.对LZW算法的改进及其在图象无损压缩中的应用[J].上海交通大学学报,1998,32(9):112-115.

[9] 华强.LZ77和LZ78在数据压缩中的组合带参运用[J].小型微型计算机系统,2000,21(2):100-104.

[10] 崔业勤,高建国.基于“虚段”方法的LZ混合无损压缩算法[J].计算机应用与软件,2007,24(3):140-141.

[11]BellTimothyC,JohnJCleary,IanHughWitten.TextCompression[M].EnglewoodCliffs:Prentice-Hall,1990.

IMPROVEMENT OF ENTROPY REDUCTION FOR LZW COMPRESSION ALGORITHMBASEDONBIGDICTIONARY

Lu Zhenlong1,2Zhang Jing1*

1(Institute of Remote Sensing and Digital Earth,Chinese Academy of Sciences,Beijing 100094,China)2(University of Chinese Academy of Sciences,Beijing 100094,China)

AbstractBased on the analysis of compression algorithm LZW, this paper puts forward an improved compression algorithm aimed at the deficiency of LZW that the average information entropy block of compressed data grows dramatically along with the increase of dictionary scale. This algorithm utilises the spatial correlation commonly existed in data, while saving the big dictionary it also narrows the range of the dictionary that actually used in each compression, so as to reduce the information entropy of the compressed data. The paper provides performance comparison between the improved algorithm and LZW compression algorithm, the result of experiment indicates that the improved algorithm achieves an optimisation by 2%～16.9% in the aspect of data information entropy after the compression is reduced.

KeywordsData compressionAlgorithmsEntropy of informationData correlation

收稿日期：2015-01-09。陆振龙，硕士，主研领域：数据压缩。张箐，教授级高工。

中图分类号TP391.7

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.06.068