城市交通中左转禁限的双层规划模型
张 珊, 樊慧敏
(长春工业大学 基础科学学院, 吉林 长春 130012)
城市交通中左转禁限的双层规划模型
张珊,樊慧敏*
(长春工业大学 基础科学学院, 吉林 长春130012)
摘要:研究了左转禁限对交通路网的影响,并应用双层规划建立数学模型,通过遗传算法对模型进行求解,从而得到最优解。
关键词:交叉口; 左转禁限; 双层规划; 遗传算法
0引言
交通网络是一个城市的血脉,它与居民的生活息息相关,所以交通拥堵成为急需解决的一个问题,我国很多学者基于交通网络提出了转弯禁限措施,并对其进行建模求解。例如,陈宽民[1]等对交通流中左转车流在交叉口的冲突特点做了详细的分析;王伟娟[2]等对交叉口的禁左限制做了深入研究;龙科军[3]和龙建成[4]等对交通网络中左转禁限问题建立了双层规划模型,并研究了如何用遗传算法对双层规划模型求解。但是这些研究理论以及其在实践中的应用并不十分完善,也存在着许多问题[5]。例如,我们通常都是在平面交叉口[6]的前提下考虑左转禁限问题的,而对于其他形式的交叉口并没有考虑,或者是在对转弯禁限研究的过程中忽略了行人对交通网络的影响。文中以交叉口是否设置左转禁限为变量,建立了双层规划模型,上层规划以交通路网中车流运行的总时间最小为目标函数,下层规划以静态用户均衡模型作为目标函数,通过改进的遗传算法对模型进行求解,从而得到最适合进行左转禁限的交叉口。
1双层规划模型的建立
1.1前提假设
为了方便考虑和建立模型,不妨假设[7]:
1)在交通网络中,每条道路的通行能力都是一定的。
2)城市的交通网络在实施左转禁限后,路网中的车道划分以及信号灯的调整符合新的交通运行情况。
1.2交叉口的选择
在左转禁限问题中交叉口的选择至关重要,如果交叉口选择不当,不仅耗费大量的人力物力,而且会给出行者带来极大的不方便。如何备选合适的交叉口可以依据以下几点考虑:
1)观察与交叉口相邻的道路,如果交叉口与其相邻的道路关系单一,呈放射性形状,那么由于此交叉口的独立性不适宜设置禁限;如果交叉口与其相邻的道路关系复杂且充分冗余,呈网状形状,那么此交叉口处可以考虑设置禁限。
2)一般选择车流量大的交叉口进行设限,而对于车流量小的交叉口不予考虑[8]。
1.3模型的建立
1.3.1上层规划模型
(1)
(2)
(3)
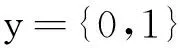
(4)
式中:xab----路段a转向到路段b的车流量;
tab----车辆由路段a转向到路段b时的时间函数;
xa----路段a的车流量;
ta----车辆通过路段a的时间函数;
y----0-1变量,当y=1时,表示禁止左转,当y=0时,表示左转;
Sa----路段a的饱和度;
Sab----交叉口ab处的饱和度;


ca----路段a的通行能力;
cab----交叉口ab处的通行能力;
A----所有路段的集合;
xa,xab----y的隐函数。
目标函数表示的是整个路网所有车辆运行的时间总和最小。
1.3.2下层规划模型
1952年著名学者Wardrop提出了交通网络平衡定义的第一原理和第二原理,奠定了交通流分配的基础。许多研究学者根据这一原理分析了交通网络流的平衡问题[9-11],下层规划模型可采用用户均衡分配模型[12-13]。
目标函数表示整个路网上的交通流量最小。
(5)
(6)
(7)
(8)
(9)
式中:R----出发点的集合;
S----目的地的集合;
qrs----连接O-D对r-s的出行需求;



1.4模型的求解
双层规划问题是一个NP-hard问题,这使得对双层规划模型的求解十分困难。由于文中所建立的双层规划模型包含了大量的二进制变量,而且需要处理大量的数据寻求全局最优解,所以,文中决定选用遗传算法[14-16]来求解双层规划模型。
求解步骤如下:
1)编码。选定n个交叉口并按顺序排列,随机产生一个长度为n的二进制串表示一个个体,其中每一位对应一个交叉口。编码1表示对应的交叉口禁左,编码0表示不禁左。
2)产生初始种群。一般随机产生20~50个群体。
3)适度函数
式中:G0----没有禁左的情况下交通网络的总阻抗。
4)选择。根据优胜劣汰的法则采用轮盘赌对种群进行选择,选出的优良个体作为父代繁殖子孙。
5)将种群中的个体配对。随机选定一个交叉位,将所有配对的染色体组该位置的基因互换。
6)变异。随机在基因串上选取一个位置,使该位置上的数字逻辑相反,即“1”变成“0”,“0”变成“1”。
7)终止条件

Fmax----所有个体中的最大适应值。
2实例论证
选取太原市某一区域路段为研究对象,应用文中模型对其制定禁限方案。道路路网如图1所示。

图1道路路网
把图中的交叉口按顺序进行编码,得到备选方案集h,种群数取50,交叉率为pc=0.5,变异率为pm=0.1,迭代50次。交叉口交通运行情况见表1。

表1 交叉口运行情况表
借助Matlab对模型求解得最优解为h={0011110000100000}。
3结语
研究了城市交通路网中交叉口设置左转禁限的问题,根据交通路网中交通流的特性建立了双层规划模型,并通过遗传算法对其求解。以太原市某一局域网为例,根据文中所建立的模型通过Matlab工具得出了相应的禁限路口。
参考文献:
[1]陈宽民,罗志忠.平面交叉口左转车流的特性分析及对策研究[J].公路交通技术,2006,4(2):114-118.
[2]王娟.网络变结构控制在交叉口流向禁限管理中的应用[D].上海:同济大学,2008.
[3]龙科军.道路网路交叉口禁左交通组织优化[J].北京工业大学学报,2011,6(6):876-881.
[4]龙建成.城市道路交通拥堵传播规律及消散控制策略研究[J].上海理工大学学报,2011,33(6):701-710.
[5]张红军.基于交通瓶颈的动态交通分配模型[J].系统工程理论与实践,2006,26(4):125-129.
[6]卢明宇,王兴.交叉口交通拥堵分析与对策[J].长春工业大学学报,2015,36(3):327-332.
[7]高自友,任华玲.城市动态交通流分配模型与算法[M].北京:人民交通出版社,2005.
[8]胡致涌,杨荣华.城市交通控制中的智能计算[J].长春工业大学学报:自然科学版,2013,34(6):681-685.
[9]刘法胜,吴大为,傅白白.组合式Wardrop条件下的交通网络流平衡[J].中国公路学报,2000,13(1):98-99.
[10]徐建闽,许伦辉.交通分配问题中用户优化平衡模型的算法研究[J].中国公路学报,1998,11(4):93-99.
[11]杜先汉.基于单向和禁左的区域交通组织研究[D].西安:西安交通大学,2009.
[12]李江.交通工程学[M].北京:人民交通出版社,2002.
[13]张红军.城市道路交叉口转弯禁限研究[D].兰州:兰州交通大学,2013.
[14]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997.
[15]张文修,梁怡.遗传算法的数学基础[M].西安:西安交通大学出版社,2003.
[16]王小平,曹立明.遗传算法----理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
Bi-levelprogrammingmodelforleftturnrestrictioninurbantraffic
ZHANGShan,FANHuimin*
(SchoolofBasicSciences,ChangchunUniversityofTechnology,Changchun130012,China)
Abstract:Theimpactofleftturnonthetrafficnetworkisstudied,andamathematicalmodelisestablishedwiththebi-levelprogramming.Thegeneticalgorithmisusedtoobtaintheoptimalsolutionforthemodel.
Keywords:intersection;leftturnprohibition;bi-levelprogramming;geneticalgorithm.
收稿日期:2015-12-05
基金项目:国家自然科学基金资助项目(11126239,11401046)
作者简介:张珊(1980-),女,汉族,吉林松原人,长春工业大学副教授,博士,主要从事最优化理论与算法方向研究,E-mail:zhangshan@ccut.edu.cn. *通讯作者:樊慧敏(1990-),女,汉族,山西原平人,长春工业大学硕士研究生,主要从事最优化理论与算法方向研究,E-mail:409847404@qq.com.
DOI:10.15923/j.cnki.cn22-1382/t.2016.3.02
中图分类号:U121
文献标志码:A
文章编号:1674-1374(2016)03-0217-04

