基于向量夹角余弦的IGOWLA算子组合预测模型

姚　成，　　袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠　233000)



基于向量夹角余弦的IGOWLA算子组合预测模型

姚成，袁宏俊

(安徽财经大学 统计与应用数学学院，安徽 蚌埠233000)

摘要：将向量夹角余弦和诱导广义有序加权对数平均(IGOWLA)算子相结合，构建了基于向量夹角余弦的IGOWLA算子的组合预测模型，并给出了优性组合预测的概念；最后，根据实例验证了该组合预测模型是科学的和有效的，且此模型是优性组合预测.

关键词：向量夹角余弦；诱导广义有序加权对数平均算子；组合预测；优性预测

鉴于各个预测方法的优劣，在对指标数据进行预测的过程中，仅使用一种方法，势必会影响预测精度.基于这一问题，Bates和Granger提出了组合预测的概念[1].在此之后，组合预测方法被广泛应用到各个领域，同时越来越多的学者将组合预测方法作为自己的研究重点，并获得了很多有价值的成果[2-7].Yager提出有序加权平均(OWA)算子[8]，但传统的组合预测方法仍存在对不同单项预测方法取固定权系数的问题，基于此，学者们从改善某种拟合误差的角度，提出了一系列基于不同算子的组合预测方法.例如，陈华友等在文献[9-11]中在以误差平方和为准则的条件下，分别依据不同的算子建立了组合预测模型，并给出了确定权系数的数学规划模型；江立辉等[12]创新性的给出了诱导广义有序加权对数平均算子(IGOWLA)的概念，并构建了根据IGOWLA算子的点预测的组合预测模型.传统的组合预测方法大都是以不断改善拟合误差平方和为基础来建立模型，从而求出权重系数，程玲华和陈华友[13]给出了依据向量夹角余弦的加权调和平均组合预测模型.本文在此基础上，结合IGOWLA算子，从向量夹角余弦出发，建立基于向量夹角余弦的IGOWLA算子最优组合预测模型，并给出了针对该模型的优性组合预测的概念，最后，根据实例验证了该组合预测模型是科学的和有效的.

1基本概念及组合预测模型

1.1IGOWLA算子

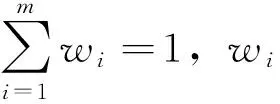
定义2[14]设〈v1,a1〉,〈v2,a2〉,…,〈vm,am〉为m个二维数组，令

(1)

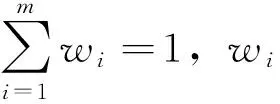
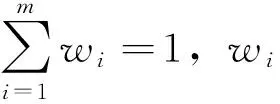
(2)

在此称GOWLAw是m维广义有序加权对数平均算子，记为GOWLA算子，将a1,a2,…am由大到小进行排序，其中第i个数即为bi，λ∈(-∞,0)∪(0,+∞).

(3)

则称函数IGOWLAw是m维广义有序加权对数平均算子，简称IGOWLA算子，其中v-index(i)是v1,v2,…,vm中第i大的元素所对应的下标，v1,v2,…,vm称为诱导变量，λ∈(-∞,0)∪(0,+∞).特殊地，若λ=1时，IGOWLA算子退化成IOGWA算子.

1.2基于向量夹角余弦的IGOWLA算子组合预测模型

假设某指标数据的实际值为xt(t=1,2,…,N)，此指标数据可以通过m种单项预测方法进行预测，xit是第i种预测方法t时刻相应的预测值(i=1,2,…,m;t=1,2,…,N).

定义5称vit为在第t时刻第i种预测方法相应的预测精度，满足

(4)

由(4)式知vit∈[0,1]，将vit记为xit的诱导值，因此，第t时刻可以得到预测精度和其对应的预测值的m个二维数组〈v1,x1〉,〈v2,x2〉,…,〈vm,xm〉.

设W=(w1,w2,…wm)T为IGOWLA算子中m种不同预测方法的加权向量，将第t时刻m种预测精度数据列v1,v2,…,vm由大到小进行排序，记v-index(i)是第i个预测精度的下标，根据定义4，可得预测精度序列v1,v2,…,vm所产生的IGOWLA算子组合预测值，记为：

在诱导广义有序加权对数平均算子的组合预测模型中，为了方便测算，对其时间序列取对数λ次幂.

对(5)式两边取对数λ次幂，得到：

(6)

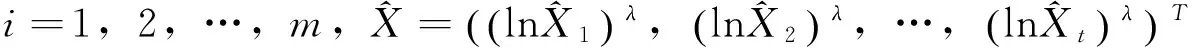
定义6令τi和τ分别为：

(7)

(8)

(9)

根据(9)式，(8)也可表示为：

(10)

τi和τ分别是第i种预测方法预测值数据列、组合预测值数据列与实际值数据列的向量夹角余弦.显然τi，τ∈[0,1],且向量夹角余弦值越大表示组合预测精度越高.

式(9)表明基于IGOWLA算子组合预测值序列与实际观察值序列的向量夹角余弦是组合预测方法的权重系数w1,w2,…wm的函数，且向量夹角余弦越大，表示组合预测方法效果越好.

因此，基于向量夹角余弦的IGOWLA算子组合预测模型表示为式(10)的最优化模型：

(11)

定义7如果τ>τmax，在此将权重w1,w2,…wm决定的组合预测模型称为优性组合预测；如果τmin≤τ≤τmax，在此将此组合预测模型称为非劣性组合预测；如果τ<τmin，在此将此组合预测模型称为劣性组合预测.

定义7说明当各个单项预测值数据列与实际值数据列的向量夹角余弦最大值低于组合预测值数据列与实际值数据列向量夹角余弦值时，将此组合预测模型称为优性组合预测模型.

2实例分析

为了验证本文提出的组合预测模型的优越性，选出五种误差对模型精度进行评价：

其中，i=1,2,…,m，表示第i种单项预测方法.

本文利用文献[16]的数据进行基于向量夹角余弦的IGOWLA算子组合预测模型的分析，实际值和预测值数据见表1.

表1　实际值与预测值数据

依据(4)式测算出2种预测方法在11个时刻的预测精度，见表2.

表2　预测精度

将表2的数据代入模型(11)中，分别取λ为1、2、3，得到基于向量夹角余弦的IGOWLA算子组合预测模型的最优权重系数，见表3所示.

表3　最优权重系数

将最优权重系数代入(12)式的基于向量夹角余弦的IGOWLA算子组合预测模型:

(12)

可以计算出不同参数λ对应的基于向量夹角余弦的IGOWLA算子组合预测值，数据见表4所示.

表4　实际值及基于向量夹角余弦的IGOWLA算子组合预测值

利用文中给出的基于向量夹角余弦的IGOWLA算子组合预测模型的精度评价指标体系，可以分别计算出两种单项预测方法和基于不同参数λ对应的IGOWLA组合预测方法的对应的预测误差，如表5所示.

表5　预测误差

由表5可以看出，在λ取1、2、3这三个值时，两种预测方法的预测误差值远大于本文给出的组合预测模型的误差值，表明了本文提出的组合预测方法好于以上两种预测方法，可以给出精度更高的预测结果.

此外，通过(7)式能够测算出两种预测方法的预测值数据列与实际值数据列的向量夹角余弦，当λ取1时，得τ1=0.999981，τ2=0.999882；当λ取2时，τ1=0.999929，τ2=0.999571；当λ取3时，τ1=0.999849,τ2=0.999107.基于向量夹角余弦的IGOWLA算子组合预测模型测算出的预测值数据列与实际值数据列的向量夹角余弦，在λ取1、2、3时分别为0.999982、0.999931、0.999850，均大于max(τ1,τ2)，故根据定义7的表述可知本文给出的组合预测模型是优性组合预测.

综上所述，可以得出基于向量夹角余弦的IGOWLA算子组合预测模型能够很好地提高预测精度，是一种行之有效的预测方法.

3结语

本文将向量夹角余弦和诱导广义有序加权对数平均(IGOWLA)算子相结合，建立了基于向量夹角余弦的IGOWLA算子的最优组合预测模型，并给出了优性组合预测的概念，最后，根据实例验证了该组合预测模型是科学的和有效的，且此模型是优性组合预测.然而本文对基于向量夹角余弦的IGOWLA算子的最优组合预测模型的一些性质，例如优性组合预测的存在性等理论问题缺乏具体的讨论，这些问题有待更深入的研究.

参考文献：

[1]Bates J M,Granger C W J.Combination of forecasts[J].Operations Research Quarterly,1969(4):45l-468.

[2]Xu Z S,Da Q L.The ordered weighted geometric averaging operators[J].International Journal of Intelligent Systems,2002(17):709-716.

[3]唐小我,马永开,曾勇,杨桂元.现代组合预测和组合投资决策方法及应用研究[M].北京:科学出版社,2003.

[4]陈华友,盛昭瀚,刘春林.基于向量夹角余弦的组合预测模型的性质研究[J].管理科学学报,2006(2):1-8.

[5]陈华友.基于相关系数的优性组合预测模型研究[J].系统工程学报,2006(4):353-360.

[6]袁宏俊,杨桂元.基于最大—最小贴近度的最优组合预测模型[J].运筹与管理,2010(2):116-122.

[7]杨桂元,罗阳,高俊.我国房地产价格组合预测模型探讨[J].统计与决策,2014(12):17-20.

[8]Yager R R.On ordered weighted averaging aggregation operators in multicriteria decisionmaking[J].Systems,Man and Cybernetics,IEEE Transactions on,1988(1):183-190.

[9]陈华友,刘春林.基于IOWA算子的组合预测方法[J].预测,2004(6):61-65.

[10]Yager R R.Generalized OWA aggregation operators[J].Fuzzy Optimization and Decision Making,2004(1):93-107.

[11]陈华友,盛昭瀚.一类基于IOWGA算子的组合预测新方法[J].管理工程学报,2006(4):36-39.

[12]江立辉,陈华友,丁芳清，等.基于IGOWLA算子的最优组合预测模型及应用[J].统计与决策,2015(4):82-85.

[13]程玲华,陈华友.基于向量夹角余弦的加权调和平均组合预测模型的有效性[J].数学的实践与认识,2008(10):102-109.

[14]Yager R R.Induced aggregation operators[J].Fuzzy Sets and Systems,2003(1):59-69.

[15]Zhou L G,Chen H Y.Generalized Ordered Weighted Logarithm Aggregation Operators and Their Applications to Group Decision Making[J].International Journal of Intelligent Systems,2010(7):683-707.

[16]杨蕾,陈华友,王宇.基于贴近度的诱导广义OWA算子最优组合预测模型[J].统计与决策,2013(5):24-26.

Combination Forecasting Model Based on Vectorial Angle Cosine and IGOWLA Operator

YAO Cheng，YUAN Hong-jun

(AnhuiUniversityofFinanceandEconomics,Bengbu,Anhui233000)

Abstract：An optimal combination forecasting model is proposed based on the combination of vectorial angle cosine and the induced generalized ordered weighted logarithmic averaging(IGOWLA)operator．The conception of superior combination forecasting are given.And it is shown that the model can improve the accuracy of combination forecasting effectively by an example calculation.

Key words：vectorial angle cosine；induced generalized ordered weighted logarithmic averaging(IGOWLA)operator；combination forecasting；superior forecasting

收稿日期：2016-03-21

基金项目：教育部人文社会科学研究青年基金项目：区间型组合预测创新方法及其有效性的研究(12YJC630277)；安徽财经大学重点科研基金资助项目：广义信息集成算子的构成及其应用的研究(ACKY1612ZDB).

作者简介：姚成，1990年生，男，安徽亳州人，硕士研究生，研究方向：经济统计；

中图分类号：O224

文献标识码：A

文章编号：1671-9743(2016)05-0025-05

袁宏俊，1978年生，男，安徽庐江人，副教授，硕导，研究方向：组合预测.