煤层钻孔有效抽采半径数值模拟研究
魏风清, 程沛栋, 张钧祥, 杜晓奇
(1.河南理工大学 安全科学与工程学院, 河南 焦作 454003;2.河南理工大学 能源科学与工程学院, 河南 焦作 454003)
煤层钻孔有效抽采半径数值模拟研究
魏风清1,程沛栋1,张钧祥2,杜晓奇1
(1.河南理工大学 安全科学与工程学院, 河南 焦作454003;2.河南理工大学 能源科学与工程学院, 河南 焦作454003)
摘要:在煤层瓦斯流动理论和弹性力学基础上,考虑煤体渗透率变化对瓦斯流动的影响,建立了含瓦斯煤岩渗流-应力耦合数学模型,根据该模型对COMSOL Multiphysics数值模拟软件进行二次开发,以某突出矿井为例建立了煤层钻孔瓦斯抽采模型,并进行求解计算,结果表明煤层瓦斯压力、煤体渗透率均随抽采时间的增加而逐渐降低,钻孔有效抽采半径随抽采时间的增加而逐渐扩大,但均具有一定的时效性;采用压力法进行现场测试,实测结果与模拟结果基本一致,证明了含瓦斯煤岩渗流-应力耦合数学模型的正确性及采用数值模拟方法计算煤层钻孔有效抽采半径的可行性。
关键词:煤层钻孔; 瓦斯抽采; 有效抽采半径; 含瓦斯煤; 渗流-应力耦合; 数值模拟
网络出版地址:http://www.cnki.net/kcms/detail/32.1627.TP.20160705.1458.007.html
0引言
煤层瓦斯抽采是煤矿防治瓦斯事故的根本性措施,在瓦斯灾害防治方面可起到较好的防突和综合治理效果[1]。钻孔的有效抽采半径是煤层瓦斯抽采的一个重要参数,直接关系到钻孔的设计、布置和抽采时间。钻孔煤层透气性、煤体孔隙压力等都会对钻孔有效抽采半径及抽采效果产生影响,因此,准确测定钻孔有效抽采半径对煤层消突效果具有重要的现实意义[2]。
目前国内外学者不断完善了煤层瓦斯流动理论[3]研究,并在此基础上,将基于计算机数值模拟的钻孔有效抽采半径确定方法应用到实际中,如采用瓦斯压力[4-5]、瓦斯流量衰减[6]、瓦斯含量[7]等指标现场测定钻孔有效抽采半径;刘军等[8]通过数值模拟方法计算钻孔有效抽采半径,但未对钻孔有效抽采半径的变化规律进行研究。本文以某突出矿井为例,建立考虑煤体孔隙压力、吸附膨胀应力的渗流-应力耦合模型,利用COMSOL Multiphysics多物理场软件模拟建立钻孔模型,并对其求解计算,模拟研究抽采过程中钻孔周围瓦斯流动规律,确定钻孔有效抽采半径并分析其变化规律,最后采用瓦斯含量指标法进行现场验证。
1瓦斯流动模型
1.1瓦斯渗流场方程
由于气体在多孔介质内的流动符合气相质量守恒定律,所以在单位时间内,控制体流入、流出的质量差等于控制体的质量变化,则瓦斯流动连续性方程为
(1)
式中:Q为单位体积含瓦斯煤岩中的瓦斯质量,kg/m3;t为时间,s;ρ为煤层瓦斯密度,kg/m3;V为瓦斯渗流速度,m/s。
煤层内瓦斯以游离态和吸附态2种方式存在。游离态瓦斯符合理想气体状态方程,吸附态瓦斯满足朗格缪尔等温吸附方程。根据参考文献[9]的煤层瓦斯含量方程和参考文献[10]的有效应力方程可得煤层瓦斯流动方程:
(2)
式中:β为煤层瓦斯的压缩因子,kg/(m3·Pa);p为瓦斯压力,Pa;φ为煤体孔隙率;a为单位质量煤的极限吸附量,m3/kg;b为煤的吸附常数,MPa-1;c为单位体积煤中可燃物的质量,kg/m3;pn为标准状况下瓦斯压力,Pa;k为煤体渗透率,m2;μ为瓦斯的动力黏度,Pa·s;m为Klinkenberg系数,Pa。
1.2煤体渗透率模型
渗透率是煤层内瓦斯流动难易程度的重要指标,也是瓦斯抽采的一项重要参数。含瓦斯煤体是一种多孔介质,在瓦斯抽采过程中,煤体孔隙压力降低、煤基质解吸效应及有效应力的改变会影响渗透率的变化[11]。考虑渗流场内瓦斯压力、瓦斯解吸和应力场煤体体积应变的影响,可得到参考文献[12]中的孔隙率方程。根据Kozeny-Carman方程可得到孔隙率与渗透率的关系,进而得到煤体渗透率方程:
(3)
式中:k0为煤体初始渗透率,m2;εv为煤体体积应变;φ0为煤体初始孔隙率;Δp为瓦斯压力变化,Pa;ks为煤体体积模量,Pa;ρs为煤体视密度,kg/m3;R为普氏气体常数,R=8.314 5 J/(kg·K);T为煤体温度,K;Vm为气体摩尔体积,m3/mol;p0为初始瓦斯压力,Pa。
1.3应力场方程
在煤层瓦斯抽采过程中,煤体多属于压缩变形。若忽略温度影响,煤体变形可认为是由地应力、瓦斯压力及瓦斯吸附膨胀产生的膨胀应力共同作用影响[13]。由含瓦斯煤体的有效应力平衡方程、煤体变形在线弹性变形阶段遵循的广义胡克定律、参考文献[14]中的煤体膨胀应力的计算公式、参考文献[12]中的煤体体积应变张量表示形式,可得出应力场煤体变形控制方程:
(4)
式中:G为剪切模量,GPa;ui,uj分别为水平方向和垂直方向的位移分量,m;υ为含瓦斯煤岩泊松比;α为Biot系数;p′为瓦斯压力分量,Pa;F为体应力,N/m3。
式(3)、式(4)共同构成了含瓦斯煤岩渗流-应力耦合模型。
2计算机数值模拟
2.1几何模型建立
计算机数值模拟以理论数学模型为基础,根据建立的含瓦斯煤岩渗流-应力耦合模型,通过对COMSOL Multiphysics软件进行二次开发,根据某突出矿井实际情况建立抽采钻孔模型,如图1所示。煤层边界为100 m×80 m,煤层中布置孔径为94 mm的抽采钻孔,孔深70 m,抽采负压为13 kPa。
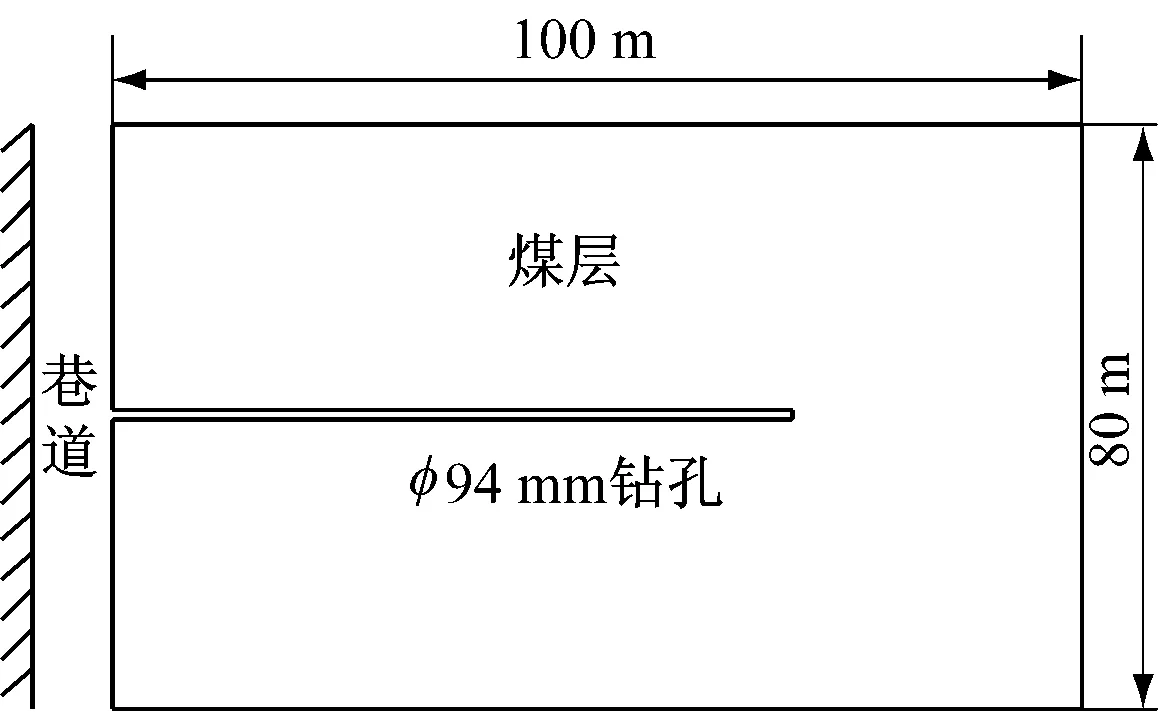
图1 抽采钻孔模型
煤层内初始瓦斯压力为1.5 MPa,应力场初始位移为0。假设瓦斯仅在煤层中流动,煤层顶底板为不透气岩层,煤层四周为自由边界。模型主要计算参数见表1。
2.2瓦斯压力模拟结果分析
图2为仿真得到的瓦斯压力分布曲线。可看出随着抽采时间的增加,煤层瓦斯压力不断降低,且与钻孔的距离越近,煤层瓦斯压力下降速率越大;随着与钻孔距离的增加,瓦斯压力逐渐增大,至煤层深部恢复至初始瓦斯压力1.5 MPa。这是由于煤层钻孔施工破坏了原始煤体的应力状态,钻孔周围形成一个卸压区域范围,该范围内煤层透气性系数增大,在抽采初期高瓦斯压力的影响下,抽采效果显著;随着时间的推移,钻孔周围的应力集中带逐渐向深部转移,煤体中孔隙被压缩,煤体渗透率减小,抽采难度加大,导致瓦斯抽采量降低。

表1 模型主要计算参数
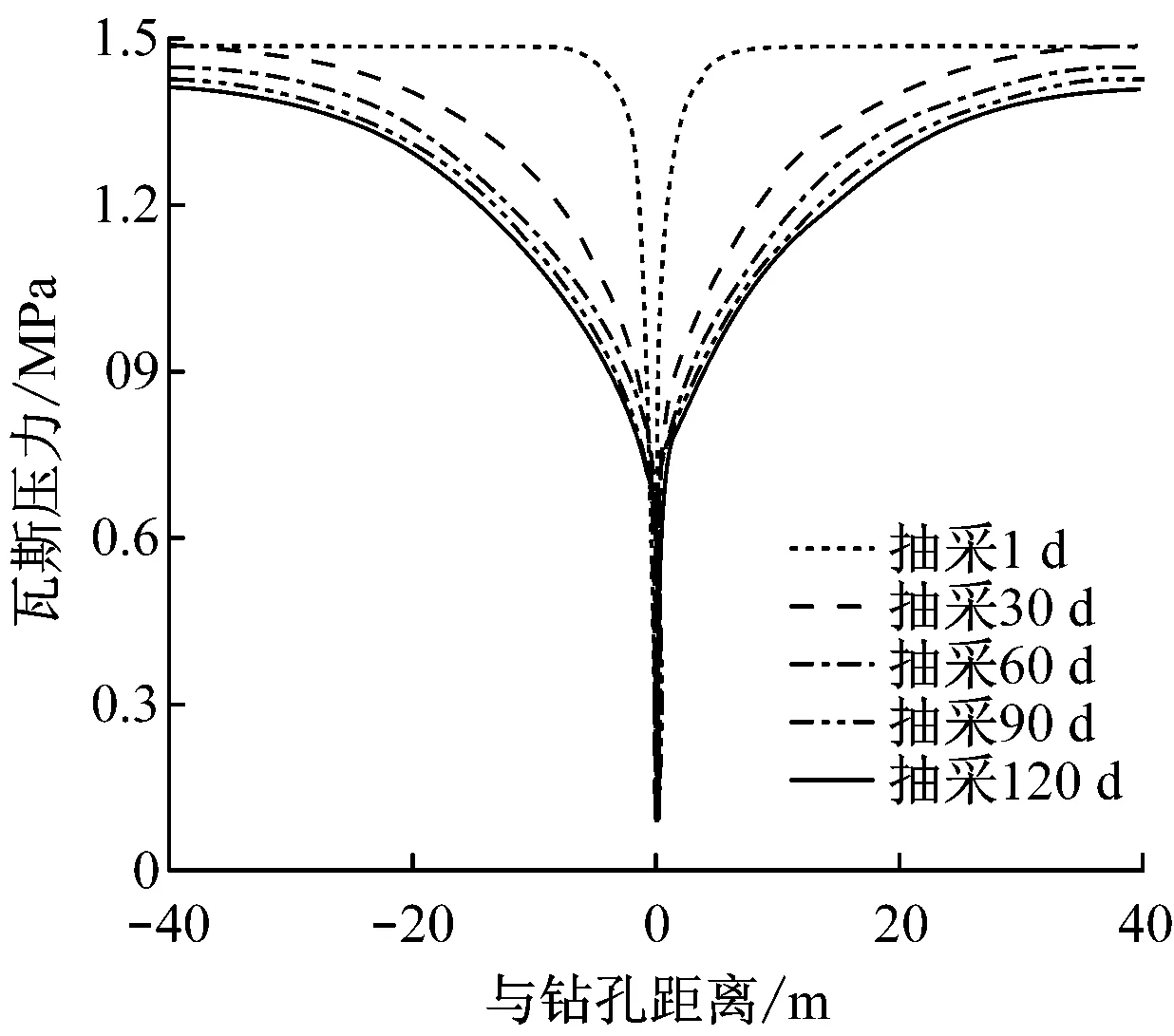
图2 瓦斯压力分布曲线
2.3煤体渗透率模拟结果分析
图3为距钻孔3 m处一点煤体渗透率变化曲线。可看出随着抽采时间的增加,煤体渗透率不断降低,且降低速率也逐渐减小。这是因为随着抽采工作的进行,煤层内瓦斯压力持续降低,煤体受到的有效应力增大,导致煤体受压,煤体内孔隙逐渐闭合。可知在实际瓦斯抽采工作中,随着抽采时间的增加,虽然煤层中瓦斯压力继续降低,但由于煤体渗透率降低,导致瓦斯压力变化量逐渐减小,钻孔瓦斯抽采量也趋于稳定。
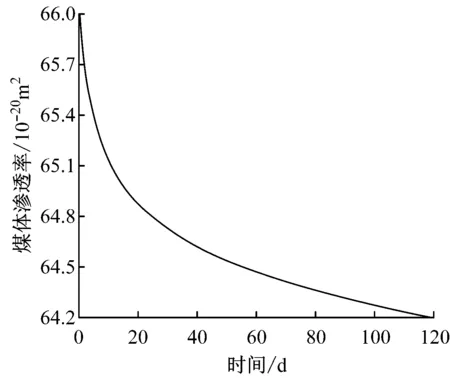
图3 煤体渗透率变化曲线
2.4有效抽采半径的确定
在瓦斯抽采工作中需要确定钻孔间距,就必须确定煤层钻孔的有效抽采半径。依据《煤矿瓦斯抽采达标暂行规定》,预期的防突效果达标瓦斯压力或瓦斯含量按煤层始突深度处的瓦斯压力或瓦斯含量取值;没有考察出煤层始突深度处的煤层瓦斯压力或瓦斯含量时,分别按照0.74 MPa、8 m3/t取值[15]。因此,本文将煤层内距钻孔最远处残余瓦斯压力小于0.74 MPa的范围确定为钻孔有效抽采半径。钻孔有效抽采半径模拟结果如图4所示。

(a) 抽采30 d

(b) 抽采60 d

(c) 抽采90 d
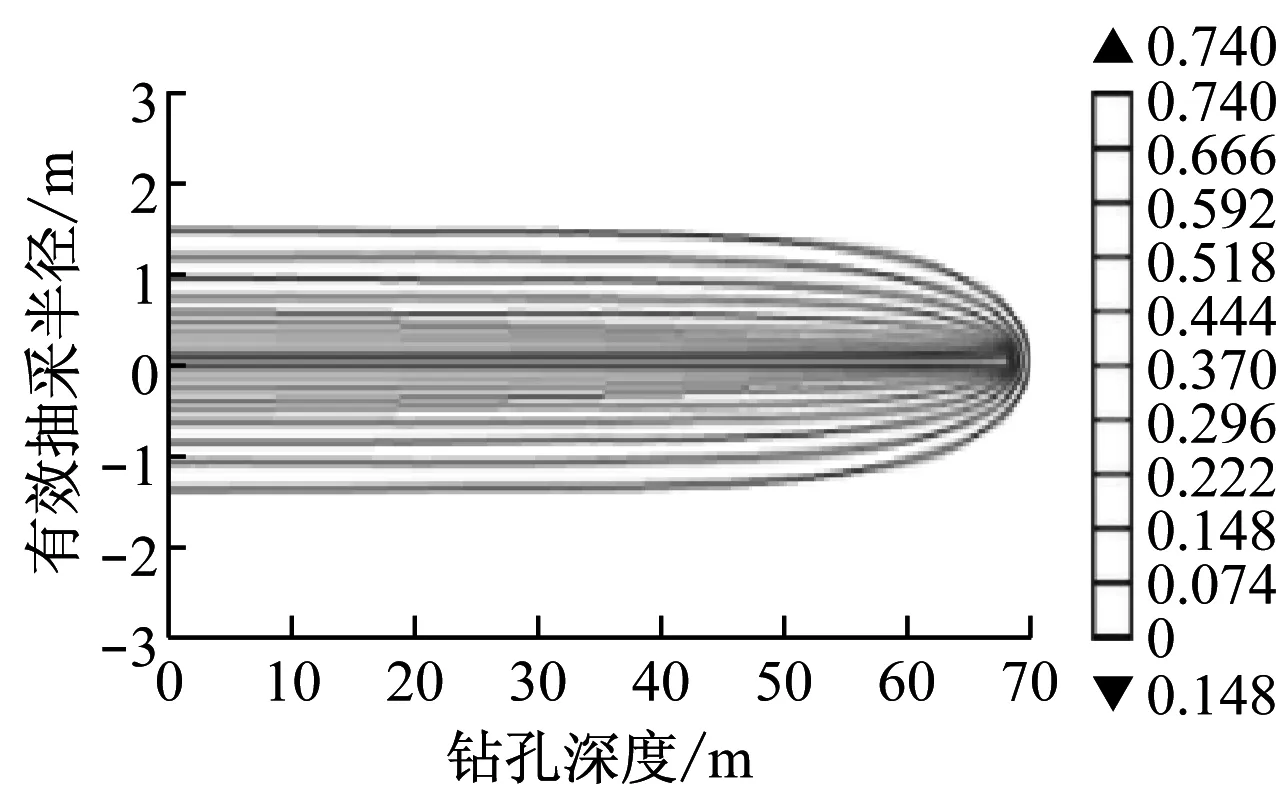
(d) 抽采120 d
从图4可看出,钻孔有效抽采半径随抽采时间的增加而增大,在抽采30,60,90,120 d条件下,钻孔有效抽采半径分别为0.52,0.96,1.27,1.41 m。为了得到有效抽采半径与抽采时间的变化规律,对模拟结果进行曲线拟合,如图5所示。可知在一定抽采时间内,有效抽采半径与抽采时间呈正比,之后随着抽采时间的增加,钻孔有效抽采半径增幅逐渐降低。结合图3可知,由于煤体渗透率随抽采时间增加而降低,钻孔抽采量不断降低,钻孔抽采瓦斯的效果会逐渐减弱,每个钻孔的控制范围也趋于稳定。
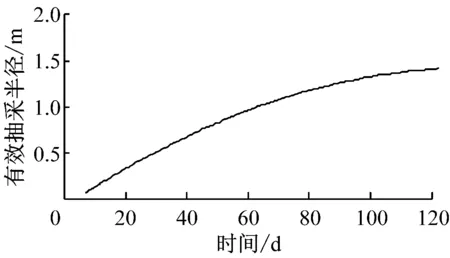
图5 钻孔有效抽采半径曲线拟合结果
3现场实测考察
3.1测试方案
测试地点位于豫南某突出矿井回采工作面。该矿仅有二1煤层全区可采,无保护层可采。煤层瓦斯含量随埋深递变规律明显,由于煤体为强破坏—全粉煤破坏类型,本煤层局部地区有可能形成高压瓦斯聚集区域。在回采工作面掘进过程中,实测煤层初始瓦斯含量最大值为7.88 m3/t,煤层原始瓦斯压力最大值为1.5 MPa。
为确保回采工作的安全进行,采用本煤层顺层钻孔抽采煤层瓦斯的区域防突措施。采用钻孔流量法对钻孔有效抽采半径进行测试,测试钻孔布置如图6所示。共布置3个测试钻孔,其中2号钻孔为抽采孔,1号、3号钻孔为观测孔,封孔深度为18 m,煤层倾角为16°,钻孔施工深度为20 m。钻孔施工完成后,每天记录数据。
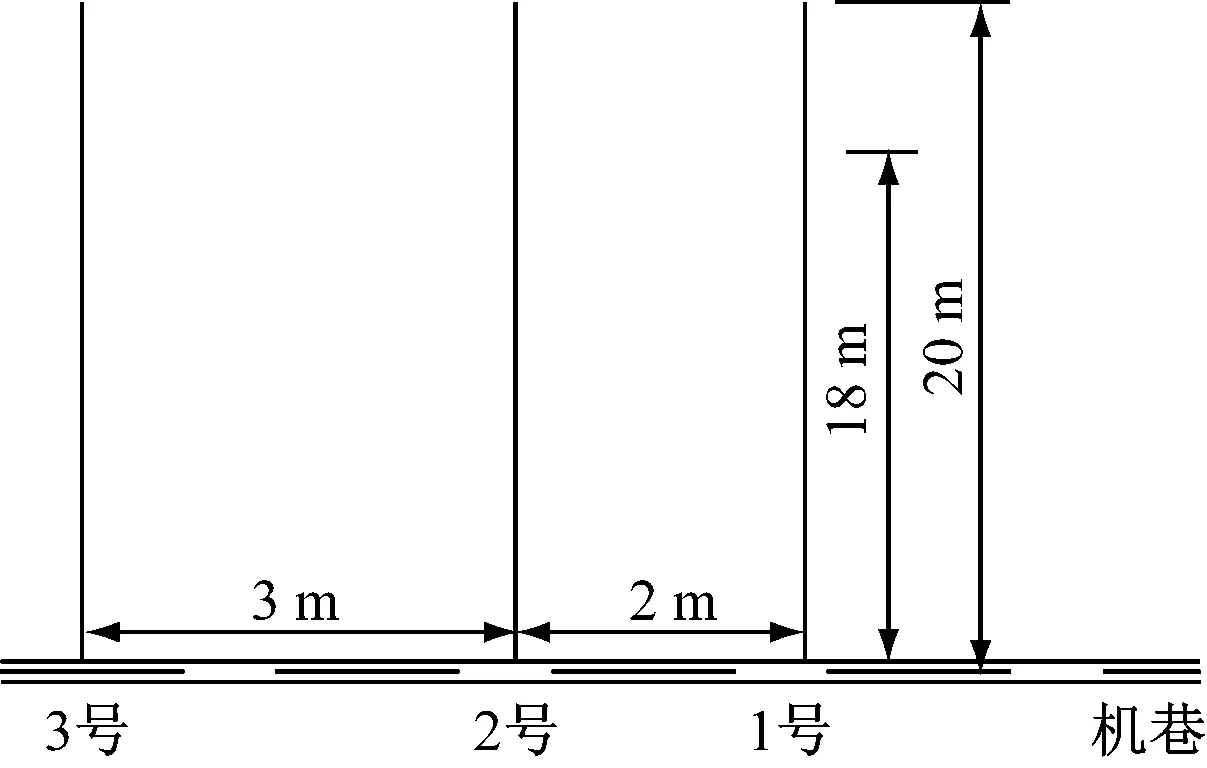
图6 测试钻孔布置
3.2数值模拟与实测结果
采用钻孔流量法对钻孔有效抽采半径进行考察,实测结果见表2。
抽采半径为94 mm、抽采负压为13 kPa时,钻孔瓦斯流量的模拟值与实测值对比如图7所示。可看出模拟值与实测值具有很好的一致性,验证了本文建立的含瓦斯煤岩渗流-应力耦合模型的正确性及采用COMSOL Multiphysics软件模拟计算煤层钻孔有效抽采半径的可行性。

表2 1号钻孔瓦斯流量测试数据
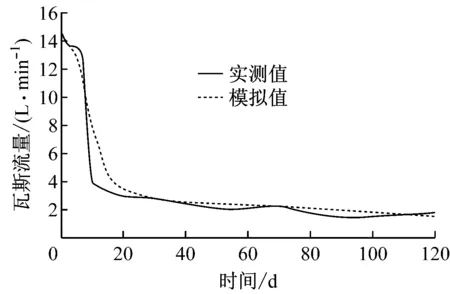
图7 钻孔瓦斯流量的模拟值与实测值对比
4结语
(1) 在瓦斯流动理论及弹性力学的基础上,考虑煤体渗透率的动态变化,建立了含瓦斯煤岩渗流-应 力耦合模型,根据该模型对COMSOL Multiphysics计算机模拟软件进行二次开发,以某突出矿井为例,建立了煤层钻孔瓦斯抽采模型。
(2) 数值模拟结果表明,煤层瓦斯压力、煤体渗透率均随抽采时间的增加而逐渐降低,钻孔有效抽采半径随抽采时间的增加而逐渐扩大,但存在一定的时效性。根据模拟结果,确定抽采120 d后钻孔的抽采范围趋于稳定,得出钻孔有效抽采半径为1.41 m。
(3) 基于瓦斯流动理论的数值模拟方法与压力法实测结果基本吻合,说明了数值模拟的准确性。因此,可通过掌握煤层瓦斯相关参数及煤层概况,方便、准确地确定煤层钻孔有效抽采半径。
参考文献:
[1]李艳增,王耀锋,高中宁,等.水力割缝(压裂)综合增透技术在丁集煤矿的应用[J].煤矿安全,2011,42(9):108-110.
[2]李建兵,陈向军.瓦斯抽采钻孔有效影响半径测定[J].能源技术与管理,2012(3):10-11.
[3]韩颖,张飞燕,余伟凡,等.钻孔瓦斯动态涌出规律的实验研究[J].煤炭学报,2011,36(11):1874-1878.
[4]孙培德.径向流场瓦斯压力分布[J].山东科技大学学报(自然科学版),1989(4):33-39.
[5]马宏宇,王兆丰,杨宏民,等.寺家庄矿下向穿层钻孔有效抽放半径研究[J].煤炭工程,2011(5):96-98.
[6]余陶,卢平,孙金华,等.基于钻孔瓦斯流量和压力测定有效抽采半径[J].采矿与安全工程学报,2012,29(4):596-600.
[7]刘三钧,马耕,卢杰,等.基于瓦斯含量的相对压力测定有效半径技术[J].煤炭学报,2011,36(10):1715-1719.
[8]刘军,孙东玲,孙海涛,等.含瓦斯煤固气耦合动力学模型及其应用研究[J].中国矿业,2013(11):126-130.
[9]张力,何学秋,李侯全.煤层气渗流方程及数值模拟[J].天然气工业,2002,22(1):23-26.
[10]HU Guozhong, WANG Hongtu, TAN Haixing, et al. Gas seepage equation of deep mined coal seams and its application[J]. Journal of China University of Mining and Technology, 2008, 18(4):483-487.
[11]魏建平,秦恒洁,王登科,等.含瓦斯煤渗透率动态演化模型[J].煤炭学报,2015,40(7):1555-1561.
[12]郭平,曹树刚,张遵国,等.含瓦斯煤体固气耦合数学模型及数值模拟[J].煤炭学报,2012,37(增刊2):330-335.
[13]李传亮,孔祥言,徐献芝,等.多孔介质的双重有效应力[J].自然杂志,1999,21(5):288-292.
[14]吴世跃.煤层气与煤层耦合运动理论及其应用的研究[D].沈阳:东北大学,2006.
[15]国家安全生产监督管理总局,国家煤矿安全监察局.防治煤与瓦斯突出规定[M].北京:煤炭工业出版社,2009.
Study on numerical simulation of effective drainage radius of drilling hole in coal seam
WEI Fengqing1,CHENG Peidong1,ZHANG Junxiang2,DU Xiaoqi1
(1.School of Safety Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China;2.School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China)
Abstract:A seepage-stress coupling model of coal containing gas was established considering effect of coal permeability changing on gas flow based on coal seam gas flow theory and elastic mechanic. The second development of COMSOL Multiphysics numerical simulation software was taken according to the model. A model of gas drainage model of drilling hole in coal seam was established taking a gas outburst mine as an example and resolved with numerical solution. The results show that coal seam gas pressure and coal permeability decrease gradurally with time extending, meanwhile effective radius of drilling hole increases gradually, and both have certain timeliness. The field test is taken by use of a pressure testing method with a result in accordance with the simulated one basically, which verifies correctness of the seepage-stress coupling model of coal containing gas and feasibility of calculating effective drainage radius of drilling hole by numerical simulation method.
Key words:drilling hole in coal seam; gas drainage; effective drainage radius; coal containing gas; seepage-stress coupling; numerical simulation
文章编号:1671-251X(2016)07-0025-05
DOI:10.13272/j.issn.1671-251x.2016.07.007
收稿日期:2015-12-30;修回日期:2016-05-12;责任编辑:李明。
基金项目:长江学者和创新团队发展计划资助项目(IRT1235)。
作者简介:魏风清(1966-),男,河南新乡人,教授级高级工程师,博士,主要从事瓦斯防治技术方面的研究及教学工作,E-mail:wfq@hpu.edu.cn。
中图分类号:TD713
文献标志码:A网络出版时间:2016-07-05 14:58
魏风清,程沛栋,张钧祥,等.煤层钻孔有效抽采半径数值模拟研究[J].工矿自动化,2016,42(7):25-29.

