双凹摩擦摆支座的设计验证及应用
夏俊勇,宁响亮,吴 滔,封 溢,王伟强,李世珩(株洲时代新材料科技股份有限公司,湖南株洲 412007)
双凹摩擦摆支座的设计验证及应用
夏俊勇,宁响亮,吴滔,封溢,王伟强,李世珩
(株洲时代新材料科技股份有限公司,湖南株洲412007)
摘要介绍了双凹摩擦摆支座结构组成及特点,分析了其适用场合。通过设计制造一个双凹摩擦摆支座,对其进行有限元分析及实体支座试验,证明了双凹摩擦摆支座经典理论基本正确,优化的屈服后刚度计算公式更准确。在制造及试验过程中发现双凹摩擦摆支座可能发生滑动面交替滑动的现象。双凹摩擦摆支座从位移最远处返回平衡位置的前半程(1 /8周期),实测滞回曲线与有限元计算得到的滞回曲线相差较大。这与以往摩擦单摆支座不同,用常规的有限元方法难以充分模拟。本文给出了相应的解释。
关键词双凹摩擦摆支座;有限元分析;试验;公式优化;应用
1 双凹摩擦摆支座
采用摩擦摆支座(Friction Pendulum Bearings,简称FPB)的基础隔震结构,在受到地震力作用产生水平位移时,FPB的刚度中心有自动与隔震结构质心重合的趋势,能在最大程度上消除结构的扭转运动,使隔震层在FPB的滑移过程中保持水平状态。FPB不仅与平面滑移隔震装置一样,对地震激励频率具有低敏感性和高稳定性,其特有的圆弧滑动面还具有自复位功能,无需附设阻尼向心机构,在实际应用中更简便可靠。近年来,越来越多的国家制定了专门的规范与规程推荐采用FPB结构隔震设计。
双凹摩擦摆相较摩擦单摆支座是一种较为新型的隔震支座,其结构见图1。
图1中,SS1为上滑动板滑动面;SS2为下滑动板滑动面;B为2个凹滑动面在竖直方向的最大间距;L为滑动板截面圆弦长;l为滑动耐磨板投影直径。
双凹摩擦摆支座主要由上下滑动板,滑动、转动耐磨板,凹球、凸球滑块组成。上下滑动板滑移面镀铬或贴覆镜面不锈钢钢板,与上下滑动耐磨板组成滑动摩擦副;凸球滑块凸球面镀铬或贴覆镜面不锈钢钢板,与转动耐磨板组成转动摩擦副,其中,上下滑动板与滑动耐磨板结构尺寸相同。
经查阅文献,发现目前国内关于双凹摩擦摆的文献大多集中于其功能与应用的理论研究,而关于双凹摩擦摆的具体结构设计验证及应用的文献较少。本文根据实际案例对此进行阐述。
2双凹摩擦摆支座的性能特点及应用
当支座上部结构发生热胀冷缩时或在地震环境下,会产生水平力。由于上下2个滑动摩擦副完全相同,根据作用力与反作用力平衡理论,双凹摩擦摆的一个滑动面滑移的位移量为S时,在另一个滑动面上将产生相同的位移量S,此时支座总的滑动位移量为2S。当承载重心发生变化时,支座上部结构会发生一定程度的挠曲变形,转动摩擦副可以消除上部结构在支座处的应力集中,这一点与摩擦单摆支座无异。
可见,双凹摩擦摆最大的特点是由2个滑动面同时提供滑动位移。在支座设计滑动位移相同时,又比摩擦单摆支座的尺寸显著减小,从而可以节省安装空间,降低造价及对安装空间的要求。
此外,根据滑动板截面圆的二次函数特性,厚度与滑动位移为正比例关系。在需要提供大位移时,摩擦单摆结构的滑动板过于厚重,双凹摩擦摆结构具有更轻的自重及更好的经济性。
因此,双凹摩擦摆特别适用于需要大位移的隔震桥梁或建筑,在西部一交通枢纽建筑上就应用了该类型支座,如图2所示。

图2 西部一交通枢纽建筑及双凹摩擦摆支座
3双凹摩擦摆支座的结构设计
3. 1材质选择
双凹摩擦摆支座在材质的选择上与摩擦单摆基本一致,对于钢材主要考虑强度与低温性能,有特别要求时考虑耐候性。
对于耐磨板,依据文献[8],转动摩擦副摩擦系数越小越好,应选择摩擦系数小的材质,且适宜涂硅油脂润滑。而对滑动摩擦副,根据实际需求选择摩擦系数适当的耐磨板,一般不适宜涂抹硅油脂。
3. 2尺寸设计
双凹摩擦摆支座中转动、滑动耐磨板,凹球、凸球滑块的尺寸设计可直接参考摩擦单摆。支座的屈服后刚度K以及等效刚度Ke均由滑动板的球半径确定,对于屈服后刚度,一般按式(1)进行计算。

式中:W为设计竖向载荷;R1,R2分别为上下滑动板面球半径,对双凹摩擦摆支座而言,R1= R2。
根据最新的摩擦摆支座等效质心理论,可按优化的屈服后刚度公式进行计算。
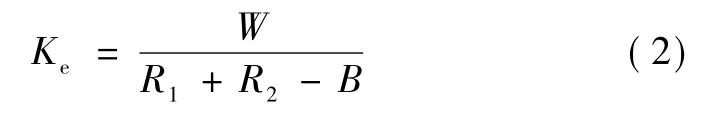
支座最大设计滑动位移D由滑动板截面圆弦长L与滑动耐磨板投影直径l共同确定。

式中,C为安全常量。
其他力学强度设计可以参考文献[9]。
4 双凹摩擦摆的设计验证
4. 1有限元仿真分析验证
1)有限元分析的基本条件
根据以上结构设计计算方法,以型号为SAB-500DX-E400-3的双凹摩擦摆支座为例验证设计方案。该双凹摩擦摆支座为多向型,设计竖向承载力为500 kN,转动摩擦系数为0. 01~0. 02,滑动摩擦系数为0. 09±15%,最大滑动位移为±400 mm,隔震等效半径为2 240 mm(对应屈服后刚度为2 232 kN/mm),支座转角为0. 02 rad。
多向型支座在正常情况(非地震)下,允许在水平任意方向发生位移。当地震发生时,多向摩擦摆支座允许在任意方向发生更大的摆动与位移。此时,多向型支座的工况覆盖了一般状态下的工况,若在地震情况下满足设计要求,则在正常使用情况下亦满足要求。因此只对地震情况进行有限元分析。
2)多向型支座地震情况下的有限元分析
采用ABAQUS 6. 10有限元分析软件对双凹摩擦摆支座进行数值模拟分析,支座铁件包括上下滑动板,凹球、凸球滑块。
铁件的材料为Q345(屈服强度345 MPa,弹性模量210 GPa,泊松比为0. 3);滑动耐磨板采用高分子量聚酯耐磨板(拉伸强度≥70 MPa,抗压强度≥120 MPa,弹性模量2. 6 GPa,泊松比为0. 4);转动耐磨板采用改性超高分子量聚乙烯(拉伸强度≥30 MPa,抗压强度≥90 MPa,弹性模量为0. 8 GPa,泊松比为0. 46)。铁件采用C3D8R六面体单元格,耐磨板采用C3D8单元格。支座共划分38 384个单元,支座有限元网格划分如图3所示。
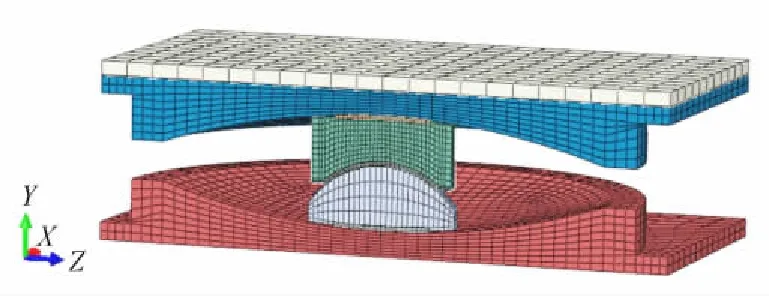
图3 支座有限元网格划分
限制上滑动板的转动自由度和下滑动板的所有自由度,对上滑动板加载500 kN竖向载荷以及±400 mm水平往复位移,记录水平力与位移的曲线,得到支座的滞回曲线。根据有限元分析结果,支座在极限位移时零部件应力最大,与预期情况一致。
支座水平滑移到转动极限位置即将向平衡位置滑移时的应力云图见图4。各零部件应力均小于材料许用强度,其中铁件受力较小,最大应力<40 MPa;转动耐磨板应力相对较大,最大应力<60 MPa,发生在转动耐磨板中心位置附近;滑动耐磨板受力最均衡,最大应力<30 MPa。
上滑动板转动0. 02 rad且滑移至最大位移时为极限状态,各零部件应力无明显增大的趋势,仍在许用强度范围内;各零部件运动无干涉,且滑块未转入转动耐磨板覆盖面,运动状况与预期情况一致。
4. 2试验验证
中车株洲电力机车研究所有限公司新材料检测中心通过了中国计量认证(China Metrology Accreditation)和中国合格评定国家认可委员会(China National Accreditation Service for Conformity Assessment)认证,试验在该中心桥梁支座专用检测2 500 t压剪试验机上进行,如图5(a)所示。竖向承载检测试验按照国标《桥梁球型支座》(GB /T 17955—2009)附录A进行。减隔震性能试验按《铁路桥梁球型支座》(TB /T 3320—2013)附录G进行,取3个滞回曲线。试验结束后拆开支座观察,如图5(b)所示。各零部件无可视变形及损坏。
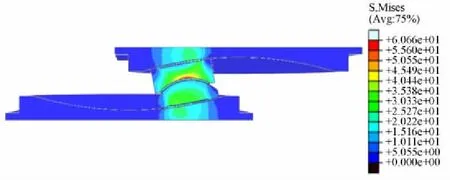
图4 支座应力云图(单位:MPa)

图5 双凹摩擦摆支座试验
4. 3试验数据分析
滞回曲线是反映双凹摩擦摆支座性能的核心数据,根据计算理论、有限元分析(FEA,Finite Element Analysis)及试验得到的滞回曲线如图6所示。
由图6可知:
1)FEA值、理论式(1)和理论式(2)的计算值十分接近,计算的屈服后刚度分别为0. 232,0. 208,0. 223 kN/mm;FEA值与理论式(1)计算值的误差为11. 5%,与理论式(2)计算值的误差为4. 0%。显然理论式(2)计算值比理论式(1)计算值更接近FEA值,说明理论式(2)具有更好的准确性。
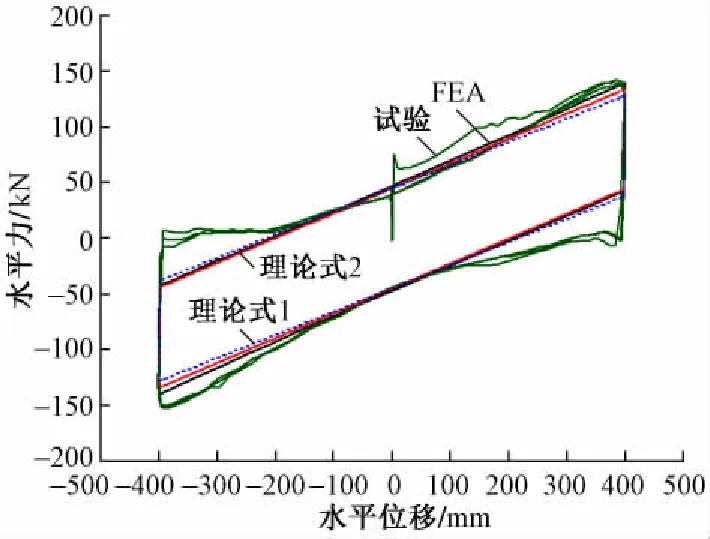
图6 双凹摩擦摆支座滞回曲线
2)实际试验滞回曲线与FEA值、理论式(1)及理论式(2)计算值比较接近,整体比较饱满。最大位移处水平反力比计算值有所增大,平均值为146 kN(不考虑水平力的方向,下同);平衡位置水平力稍小,平均值为42 kN,在平衡点处计算摩擦系数为0. 084。双凹摩擦摆支座从位移最远处返回平衡位置的前半程(1 /8周期)实测滞回曲线与理论滞回曲线相差较大,造成了滞回环面积更大,理论上耗能能力更好。合理减少这段滞回曲线的影响,计算得到实测屈服后刚度为0. 243 kN/mm,处于合理的偏差范围内。
值得注意的是,从位移最远处返回平衡位置的前半程(1 /8周期)双凹摩擦摆支座实测滞回曲线与理论滞回曲线的偏差,与摩擦单摆支座相比要明显增大。这主要是因为双凹摩擦摆支座的零部件更多,存在装配间隙,造成双凹摩擦摆支座在试验机上从最远位移处返回平衡位置过程中的实际自由度更高。
另外,在实际的试验过程中,双凹摩擦摆支座与摩擦单摆支座相比更易出现锯齿形的滞回曲线。这是因为实际制造过程中,难以保证2个滑动摩擦副的性能完全一致,2个滑动面可能交替滑动,而非预期的同时滑动。当滑动面SS1开始滑动时,滑动面SS2可能还处在静摩擦状态,直至滑动面SS1的滑动摩擦力与水平刚度提供的总水平力大于滑动面SS2提供的静摩擦力,滑动面SS2才开始滑动。因滑动面SS2从静摩擦状态突然转向动摩擦状态,水平力会突然减小,滑动面SS1会停止滑动,滑动面SS2滑动的水平力因水平刚度的存在逐渐增大,水平力-位移曲线会呈锯齿状。如此反复,每小段上升曲线实际是一个摩擦单摆的曲线。
要保证双凹摩擦摆支座曲线的连续平滑,对其2个滑动表面(包括半径尺寸、轮廓度、表面粗糙度等)的一致性都提出了远高于摩擦单摆支座的要求。因此,需要支座厂家具有很高的生产过程控制能力,但制造成本也会相应增加。
5 结论
1)双凹摩擦摆支座的结构理论,通过FEA及试验实测均能得到良好验证。在大位移工程中可以采用双凹摩擦摆支座,其具有较好的经济性,尤其适用于对支座安装空间有限制的工程。但其相对复杂的结构特性,对制造过程提出了相比摩擦单摆支座更加严苛的要求,从而提高了制造难度与成本,须综合考虑实际情况来选用这2种支座。
2)经验证,双凹摩擦摆支座屈服后刚度计算公式,在算例中精确度更高,可为业内人员提供参考。
参考文献
[1]焦驰宇,胡世德,管仲国. FPS抗震支座分析模型的比较研究[J].振动与冲击,2007,26(10):113-117.
[2]龚健,周云.摩擦摆隔震技术研究和应用的回顾与前瞻(Ⅰ)——摩擦摆隔震支座的类型与性能[J].工程抗震与加固改造,2010,32(2):1-10.
[3]XIA J Y,NING X L,TAN P,et al. Impact of the Equivalent Center of Mass Separating from the Sliding Surface on the Isolation Performance of Friction Pendulum Bearings[J]. Earthquake Engineering and Engineering Vibration,2015,14(4):695-702.
[4]冷新云,夏俊勇,郭红峰,等.摩擦摆支座结构设计及验证[J].铁道建筑,2013(5):45-48.
[5]刘昕铭,王少华,严情木,等.摩擦摆隔震支座阻尼特性研究[J].铁道建筑,2012(4):10-13.
[6]邓雪松,龚健,周云.双凹摩擦摆隔震支座理论分析与数值模拟研究[J].广州大学学报(自然科学版),2008,9(4):71-77.
[7]夏俊勇,郝红肖,胡宇新,等.摩擦摆支座球面曲率对摩擦副等效摩擦系数的影响[J].铁道建筑,2013(10):37-39.
[8]European Committee for Standardization. EN 15129 Anti-seismic Devices[S]. Brussels:European Committee for Standardization,2009.
[9]European Committee for Standardization. EN 1337-7:2001 Structural Bearings—Part 7:Spherical and Cylindrical PTFE Bearings[S]. Brussels:European Committee for Standardization,2001.
(责任审编郑冰)
Design Verification and Application of Double Concave Friction Pendulum Bearing
XIA Junyong,NING Xiangliang,WU Tao,FENG Yi,WANG Weiqiang,LI Shiheng
(Zhuzhou Times New Material Technology Co.,Ltd.,Zhuzhou Hunan 412007,China)
AbstractT he structural composition of double concave friction pendulumbearing was introduced and its application occasions were analyzed in this paper. T he FEA(Finite Element Analysis)and solid bearing test were carried out by designing and making a double concave friction pendulum bearing,which proved that the classical theory of double concave friction pendulum bearing was basically right and the optimized post-yield stiffness calculation formula was more accurate. W hile in the process of making and testing the bearing,it is found that the sliding surfaces of the bearing might slide alternatively. In the former range of the displacement(1 /8 of the cycle),when the double concave friction pendulum bearing come back to the equilibrium position from the most remote displacement point,the actual measured hysteretic curve is largely different from that deduced through FEA,which is different from friction simple pendulum bearing and very difficult to simulate thoroughly with conventional FEA,so this paper also makes explanations for these phenomena.
Key wordsDouble concave friction pendulum bearing;Finite element analysis;T es;Optimized formula;Application
中图分类号U443. 36
文献标识码A
DOI:10. 3969 /j. issn. 1003-1995. 2016. 06. 06
文章编号:1003-1995(2016)06-0023-04
收稿日期:2015-11-20;修回日期:2016-01-22
作者简介:夏俊勇(1984—),男,工程师。

