大跨径连续刚构桥合龙顶推力计算分析

李彦兵　李少杰（中交公路规划设计院有限公司贵州分公司，贵州　贵阳　550000）



大跨径连续刚构桥合龙顶推力计算分析

李彦兵李少杰
（中交公路规划设计院有限公司贵州分公司，贵州贵阳550000）

摘要：结合重庆南川至贵州道真高速公路某连续刚构桥工程实例，阐述了该桥型合龙过程中所受到的影响因素，分析了桥梁墩顶偏位与顶推力之间的关系，并推演出相应的顶推力计算过程，为今后类似桥型的合龙施工提供了参考。

关键词：连续刚构桥，顶推力，合龙施工，计算模型，位移

随着交通事业的发展，预应力混凝土连续刚构桥由于其在纵向拥有很好的抗弯刚度和横向的抗扭刚度，并且其悬臂施工方便，行车平顺，逐渐成为了大跨径桥梁施工的首选方案。

但由于连续刚构墩梁固结的特点，在产生竖向挠度的同时，也会使主墩产生一定的水平位移。在合龙施工过程中，考虑到后期收缩徐变及现场合龙温度与设计温度差值的影响，应在合龙段两侧施加顶推力，以消除上述两者所产生的水平位移。

1　工程概况

重庆南川至贵州道真高速公路某大桥为大跨度预应力混凝土刚构桥，其跨径布设为85 m +148 m +85 m，该桥左右幅桥分幅设置，两幅桥间距0.5 m，单幅桥桥面总宽12 m，桥面行车道宽11 m，两侧各设0.5 m宽的防撞护栏。跨中合龙段梁高3.3 m，0号块根部梁高9.20 m，单“T”构从中跨跨中渐变至箱梁根部，以1.75次抛物线变化。结合实际施工现场及工程进度要求，主梁悬臂浇筑梁段长度共划分为4.0 m，4.7 m两种节段，合龙段为2 m。

2　合龙顶推力计算分析

2.1墩顶偏位与顶推力关系

在结构有限元计算模型中（见图1），采用施加纵向水平集中荷载P的方式，在中跨合龙前（即最大悬臂状态下）对桥跨结构进行模拟顶推，来进一步判断墩顶水平位移的大小。

在最大悬臂端分别施加0 kN，100 kN，200 kN，300 kN的顶推力，两个主墩墩身对应在0号块中心的节点（28号、76号节点）处的水平位移见表1。

表1　顶推力下主墩水平位移（合龙温差为0）　mm

从表1中可以看出，控制截面节点的水平位移变化基本与顶推力呈线性规律，即每增加100 kN的顶推力，1号墩对应0号块中心处水平偏位为7.50 mm，2号墩对应0号块中心处水平偏位为6.05 mm。有了上述节点位移量与顶推力的关系，即可开展顶推力优化计算。

2.2顶推力计算

1）收缩徐变对顶推力的影响。在确定桥梁在运营一段时间后因收缩徐变影响所需的实际水平方向偏位量时，需要从以下两个因素考虑：

a.理论上的顶推量应为桥梁长期收缩徐变后纵向水平位移的累积，建立的有限元分析模型是对桥梁自身结构理想状态的模拟，而实际情况下的桥梁边跨支座位移肯定会受到摩阻力的影响。

b.桥梁从成桥状态到收缩徐变过程的完成需要较长的时间，假如预先顶推全部收缩徐变效应值，桥梁结构在合龙完成后的运营阶段，将会产生由于顶推作用而引起的反向过大位移，并且在此期间将有活荷载的作用，将会对运营期的桥墩产生较大的不利弯矩，更有可能引起开裂。另外双薄壁墩一般采用柔性墩，设计上考虑容许一定的纵向位移。

根据相关工程经验，一般只需预顶实际收缩徐变量的60%。考虑桥梁运营十年后，主墩对应0号块中心处节点位移如表2所示。

表2　桥梁运营十年后纵向位移　mm

在顶推力Pi作用下，各节点的水平位移量可按式（1）计算：

δi=δ1 - i×Pi（1）

δi=60%×δ10（2）

即：Pi=δi/δ1 - i（3）

其中，δi为各节点顶推产生的水平位移；δ1 - i为单位顶推力作用下各节点水平位移；Pi为顶推力；δ10为桥梁运营十年后节点累计水平位移。

通过表1，表2及式（3），可计算出：

P28=δ28/δ1 -28=27.60/7.50 =368 kN；

P76=δ76/δ1 -76=27.1/6.05 =448 kN。

中跨合龙前对两悬臂端顶推时，为了便于施工，两个中跨合龙段的顶推力应保持相等，即|P28| = P76。因此顶推力P1=（|P28| + P76）/2 =408 kN。

2）合龙温度对顶推力的影响。在实际的施工环境中，当时的合龙温度往往与设计合龙温度有一定差值，由于桥梁合龙后升温情况相比较降温情况对结构受力更为有利，故尽量选择低温环境合龙。

为分析在设计温度情况下合龙后，降温对结构的有利影响，选取计算了5个降温值工况对主墩相对应的0号块中心节点水平位移的影响，结果见表3。

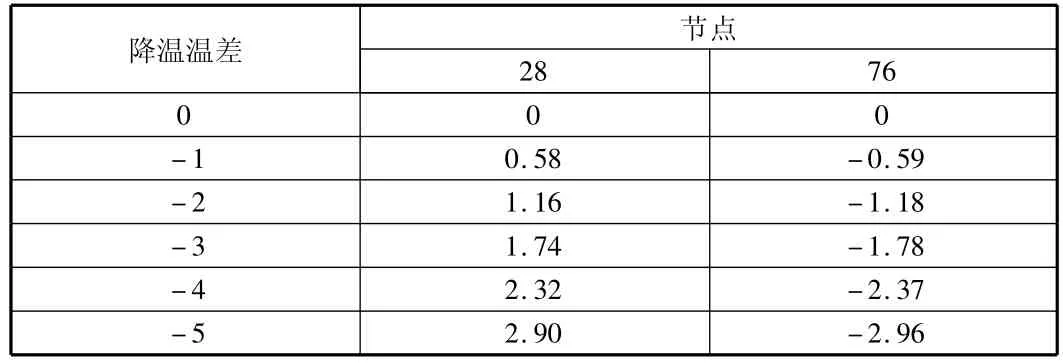
表3　合龙后降温作用下对应节点水平位移　mm

根据表3高温合龙下相对应的水平位移，则可计算出单独考虑高温温差所需采用的顶推力值，见表4。

表4　高温合龙下考虑温差对应顶推力值

3）最终顶推力的确定。

综合考虑到混凝土收缩徐变、合龙温度、结构体系转换等影响因素下，最终顶推力值如下：

P = P1+ PΔT。

值得注意的是，当桥梁在低于设计温度合龙时，相应的顶推力也应由两者的代数和来确定，不能一味地相加或者相减。

3　结语

大跨径连续刚构桥合龙过程中的顶推力施工环节尤为重要，不仅对后期跨中竖向下挠起到缓解的作用，同时平衡主墩水平偏位，改善桥梁的受力分布，从而增强了后期结构的安全性。

参考文献：

［1］范立础.桥梁工程（上册）［M］.北京：人民交通出版社，2001.

［2］徐君兰.大跨度桥梁施工控制［M］.北京：人民交通出版社，2000.

［3］邹毅松，单荣相.连续刚构桥合龙顶推力的确定［J］.重庆交通学院院报，2006（2）：13-15.

［4］李亚林，周玮.连续刚构桥顶推力计算方法及受力性能分析［J］.交通科技与经济，2006（5）：7-8.

［5］杨虎根，陈云海.公路桥梁结构设计系统在施工控制中的应用浅析［J］.公路交通科技，2006（1）：15-16.

On calculation and analysis of jacking force at closure of large-span continuous rigid bridges

Li Yanbing Li Shaojie
（Guizhou Branch，CCCC Highway Consultants Co.，Ltd，Guiyang 550000，China）

Abstract：Combining with some continuous rigid bridge project along Nanchuan-Daozhen Expressway，the paper illustrates the factors in the closure process of the bridge，analyzes the relationship between the pier top deviation and jacking push of the bridge，and deduces the calculation process of the jacking push，so as to provide some reference for the closure construction of similar bridges.

Key words：continuous rigid bridge，jacking push，closure construction，calculation model，displacement

中图分类号：U445.4

文献标识码：A

文章编号：1009-6825（2016）06-0168-02

收稿日期：2015-12-15

作者简介：李彦兵（1986-），男，硕士，工程师