时延情形下的分布式随机无梯度优化算法

任芳芳，李德权

(安徽理工大学理学院，安徽　淮南　232001)



时延情形下的分布式随机无梯度优化算法

任芳芳，李德权

(安徽理工大学理学院，安徽淮南232001)

摘要：由于多个体系统在信息交流的过程中存在通信时延，系统会出现接收信息滞后的情况，从而影响优化算法的收敛速度。为了解决时延对优化算法产生的影响， 提出了时延情形下的多个体系统分布式随机无梯度优化算法。假定系统中每个个体仅知道其自身的局部目标函数，利用系统中个体间交互时延信息来寻求这些局部目标函数之和的最小值， 通过系统扩维将有时延的优化问题转化为无时延的优化问题。由于个体的局部目标函数有可能非凸故其次梯度不一定存在或很难计算，因而采用分布式随机无梯度方法。理论分析表明只要个体间的通信时延有上界，所提算法依然收敛。

关键词：多个体系统；分布式优化；随机无梯度；通信时延

近年来，多个体分布式凸优化问题及其优化算法引起了人们的广泛关注，而多个体分布式优化算法是在集总式算法的基础上发展起来的。所谓集总式算法是指在多个体系统中，不是所有个体都发挥同样的作用，只有某个个体处于中心地位，负责处理其他个体的数据，并将数据反馈给其他个体。和集总式算法不同，分布式算法则是指多个体系统中的每个个体都对应着一个局部凸目标函数，并且个体之间进行信息交流，最终求得凸目标函数的最小值。和以往的集总式算法相比，分布式算法有很多优点，尤其在许多大规模的优化问题中占有很大优势，并且在生物工程、人工智能等许多领域有广泛应用，因此研究多个体的分布式优化算法有很大的意义。

随着计算机的广泛应用，人们进入了大数据云计算的时代，因此对多个体分布式优化的研究也越来越深入。但这些方法主要是标准次梯度和一致性算法的结合。标准次梯度算法是将总的最优化任务分解，同时每个个体需要将自身的信息与周围邻居个体的信息进行加权组合，再根据自身的次梯度信息进行最优化，经过一系列的迭代运算，使得所有个体的状态都达到一致。事实上，一致性算法也是广泛研究的一个课题，即个体间通过信息交流使所有个体的状态最终达到一致并使结果达到最优。文献[1]最早给出了标准次梯度方法并分析了其收敛性。文献[2]922介绍了约束一致性和优化算法。在此基础上，文献[3]则介绍了基于随机投影的次梯度算法，文献[4]1715给出一种基于一致性算法的原始对偶次梯度方法。在文献[4]1720的启发下，文献[5-6]提出了一种分布式对偶平均算法(DDA)以及基于Push-sum的DDA算法。上述研究都是适用于多个体系统中的每个个体对应的局部目标函数存在凸函数且次梯度的情况。而文献[7-8]研究的是个体的局部目标函数是非凸的、次梯度不存在或很难计算的情况，因此文献[9]提出了一种分布式随机无梯度优化算法。

然而，以上都是假设在任何时刻每个个体都可以即时的和周围个体之间进行信息交流。而在文献[10-12]1108中，由于有限的带宽，随机的传输延迟以及不确定的连接拓扑，个体之间的信息交流可能出现延时的情况。为此，文献[12]1139给出了时延情形下的分布式次梯度优化算法以及具有通信时延的二阶系统一致性。

本文主要研究时延情形下的分布式随机无梯度优化算法。

1符号说明

2问题描述

考虑如下由n个个体组成的多个体系统分布式凸优化问题：

(1)

这里h(x)为目标函数，x∈Rm是一个全局决策向量，hi∶Rm→R是个体i(i∈V)的自身目标函数并仅为个体i知道，同时假设其是Lipschitz连续的且Lipschitz常数为G0(hi)，X⊆Rm是非空闭凸集。式(1)表明整个系统的目标函数可以分解成系统中各个个体自身目标函数之和。

设式(1)的最优值h*是一个确定的有限值，并记最优解集为X*，

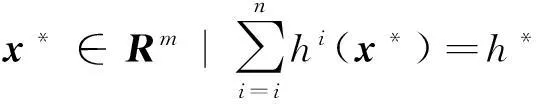
(2)

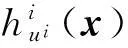
(3)

3算法介绍

3.1DRGF法

在实际情况中，由于多个体在信息交流的过程中存在通信时延，为此提出如下的时变时延情形下的分布式随机无梯度优化算法(DRGF法)。

1) 初始化

① 选择一个随机向量xi(0)∈X，∀x∈X；

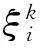
2) 迭代

② 计算xi(k+1)=ΠX[θi(k+1)-ηkgui(xi(k))]，这里ΠX[x]代表向量x到集合X上的投影，通过投影将约束集中的个体与其他个体分开，只讨论在约束集中的个体。

这里的ηk>0是迭代步长，且步长满足：

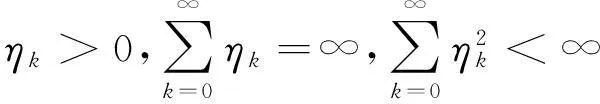
随机无梯度的预测值可表示为：

gui(xi(k))=

采样电路主要是由3个电流采样电路和4个电压采样电路构成。采样方式方面选择信号隔离的采样的方式。电压信号的采样在此选用微型精密电压互感器ZMPT107。电流采样方面选用微型精密电流互感器ZMCT101B。实验装置中电流的最大值不到 1 A,测量电阻选用Ro=500 Ω,输出电压峰峰值为 1.0 V。由于开关管的高频动作,采样信号中存在很大的高频谐波分量,采用一个截止频率fc=10 kHz,阻尼系数ζ=1.45的巴特沃斯滤波器进行滤除。

3.2系统扩维

为了方便研究时延情形下的分布式随机无梯度优化算法的收敛性，下面将介绍如何利用系统扩维把有时延的优化问题转化为无时延的优化问题。在网络图G(k)中增加一些虚拟节点(见图1)，这些节点的作用只是为了消耗信息在系统传递中的时延，自身没有自环。和增加的虚拟节点相比，网络中真实存在的点不仅可以传递信息，自己也可以处理信息。因此可以看出，虚拟节点只起到信息传递的作用，而不参与算法的迭代。

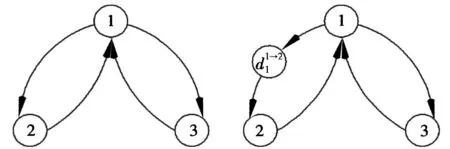
图1

4收敛性分析

首先，做出如下假设：

假设1对于有向图G以及任意有向边上的时变时延cij(k)，有：

1)有向图G是强连通图，其所对应的邻接矩阵Φ(k)是行随机的，而不一定是双随机的；

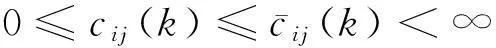
为了方便分析DRGF算法的收敛性，给出下列引理：

引理1[7]1 122对每一个i∈V有以下结论成立：

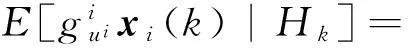
3)随机无梯度的预测值gui(xi(k))满足：

引理2[2]777令Ψ(k·s)=[Φ(k)Φ(k-1)，…Φ(s)]，则可得以下结论：

定理1在假设1，引理1成立的情况下，用上述DRGF法生成一个序列{xi(k)}k≥0，这里假设每一个hi都是Lipschitz连续的， 则对每一个t≥1和 j∈V，有：

(4)

证明首先定义一个迭代更新xi(k+1)，则有：

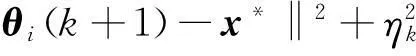
(5)

欧几里得投影满足：

‖ΠX(a)-ΠX(b)‖≤‖a-b‖，则有：

E[‖xi(k+1)-x*‖2︳Hk]≤‖θi(k+1)-

x*‖2+ηk2E[‖gui(xi(k)‖2︳Hk]-

η0E[‖gui(xi(k)‖2︳Hk]T(θi(k+1)-x*)≤

(6)

则由引理1中的1～3三条可得：

(7)

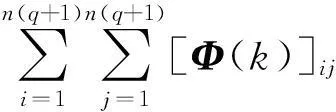
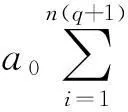
(8)

另外一方面：

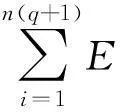
其中Ωk=E[‖xj(k)-xi(k)‖]

再有：

(9)

这里的hi是lipschitz连续的，最后可得：

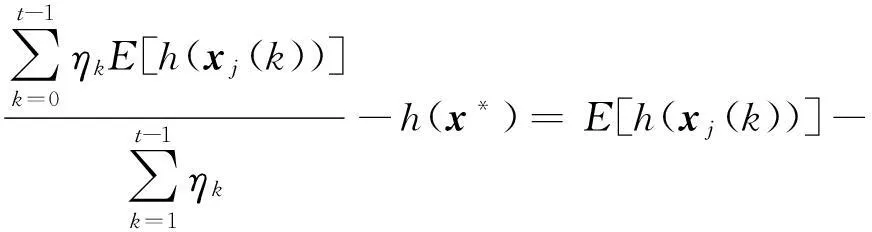
(10)

定理1给出了目标函数的期望值E和最优值h(x*)之间的误差，不难看出，该误差和个体数n，系统扩维后增加的节点数nq，迭代步长η和Lipschitz常数有关。由定理1看出只要通信时延cij有上界，算法依然收敛。当cij=0时，则转化为无时延的情况。此外，还可以看出，时延情形下的迭代误差比无时延的迭代误差大，这表明若个体在信息交流的过程中存在通信时延，则会对个体间协同解决优化问题造成一定的影响。

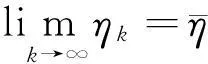
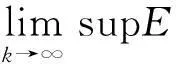
(11)

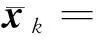
证明首先，介绍一个辅助序列：

通过循环迭代可以得到：

另一方面，由权重矩阵Φ(k)的性质和引理2可得：

(12)

进一步可得：

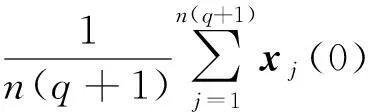
(13)

由引理3，对于意k≥s，有：

︳[Φ(k∶s)]ij-φj(s)1︳≤

(14)

定义φj(τ)=‖ΠX[θj(τ+1)-

γτgμj(xj(τ))]-θj(τ+1)‖≤ητ‖guj(xj(τ))‖

由引理1中E[‖gμj(xj(τ))‖︳Fτ]≤(m+4)G0(fj)

可得：

(15)

故推论1得证。

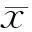
(16)

证明首先易得：

(17)

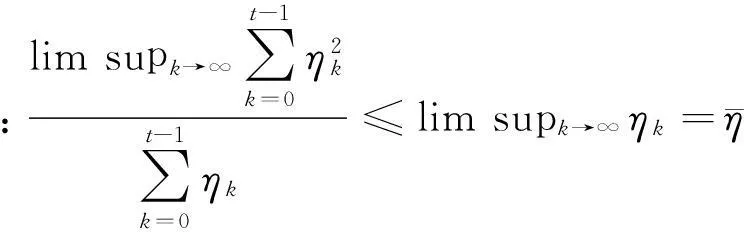
则

(18)

将推论1中的结论带入式(18)得

(19)

利用定理1，将式(18)～式(19)带入式(10)，最终可得：

(20)

事实上，定理2表明误差值lim supt→∞

6结束语

在文献[2，7]的基础上，本文研究了时延情形下的分布式随机无梯度优化算法。首先给出时延情形下的分布式随机无梯度方法，然后通过系统扩维将时延优化问题转化为无时延优化问题，并利用转移矩阵的相关结论分析并证明了其收敛性。当然，还有一些问题有待解决，比如在无向图网络拓扑下中有时延的随机无梯度算法以及切换网络下的优化算法。

参考文献：

[4]DY，SX，HZ.DistributedPrimal—DualSubgradientMethodforMultiagentOptimizationviaConsensusAlgorithms[J].IEEETransactionsonSystemsMan&CyberneticsPartBCybernetics， 2011，41(6)：1 715-1 724.[5]DUCHIJ，AGARWALA，WAINWRIGHTM.DualAveragingforDistributedOptimization：ConvergenceAnalysisandNetworkScaling[J].IEEETransactionsonAutomaticControl， 2012， 57(3)：592-606.

[6]TSIANOSKI，LAWLORS，RABBATMG.Push-SumDistributedDualAveragingforconvexoptimization[C]//IEEEConferenceonDecision&Control， 2012.

[7]NESTEROVY.Randomgradient-freeminimizationofconvexfunctions[J].GeneralInformation，internationalassociationforresearchandteaching， 2011， 36(16)：1 112-1 142

[8]LIJ，WUC，WUZ，etal.Gradient-freemethodfornonsmoothdistributedoptimization[J].JournalofGlobalOptimization， 2015， 61：325-340.

[9]YUAND，HODWC.RandomizedGradient-FreeMethodforMultiagentOptimizationOverTime-VaryingNetworks[J].IEEETransactionsonNeuralNetworks&LearningSystems， 2015， 26：1 342-1 347.

[10]TSIANOSKI，RABBATMG.Distributedconsensusandoptimizationundercommunicationdelays[C]//49thAnnualAllertonConferenceonCommunication，Control，andComputing， 2011：974-982.

[11]李德权，张晓倩. 时延情形下的分布式Push-sum次梯度优化算法的研究[J].安徽理工大学学报(自然科学版)，2015，35(2)：6-12.

[12]刘德进， 刘成林. 具有通信时延的离散时间二阶多个体网络的一致性问题[J]. 控制理论与应用， 2010， 27(8)：1 108-1 158.

[13]ABONDYJ，SRMURTYU，ABONDYJ，etal.GraphTheorywithApplications[J].AmericanElsevierPublishingCo.inc.newYork，1976，62(419)：379-381.

(责任编辑：何学华)

Randomized Gradient-free for Distributed Optimization Algorithm with Communication Delay

REN Fang-fang，LI De-quan

(School of Science, Anhui University of Science and Technology, Huainan Anhui 232001, China)

Abstract:Considering the delay of information communication among agents, which affect the convergence speed of the algorithm, the randomized gradient-free method for multi-agent optimization with communication delay was proposed, where it's assumed that every agent only knows its own local objective function. The optimization goal is to minimize a sum of local objective functions through the interaction of delay information among agents in the system. Firstly, the optimization problem with delay was converted into the optimization problem without delay through augmenting delay nodes. Because the local objective function of agent is likely to be nonconvex, its subgradient does not exist or it is hard to be calculated, the distributed randomized gradient-free method was used. The theoretical analysis showed that the proposed algorithm is still convergent if the communication delays are upper bounded.

Key words:multi-agent system; distributed optimization; randomized gradient-free, communication delay

收稿日期：2015-05-16

基金项目：国家自然科学基金资助项目(61472003)，国家自然科学青年基金资助项目(11401008)，安徽省教育厅自然科学研究重点资助项目(KJ2014A067)

作者简介：任芳芳(1990-)，女，安徽宿州人，在读硕士，研究方向：分布式优化理论与应用。

中图分类号：TP13

文献标志码：A

文章编号：1672-1098(2016)01-0034-06