可靠性多学科优化在重型车车架设计中的应用研究
郝 琪,吕 鹏,吴胜军,汪 波,吕 钧
(1.湖北汽车工业学院 汽车工程学院,湖北 十堰 442002;2.湖南大学 机械与运载工程学院,湖南 长沙 410205;3.十堰市精密制造有限公司,湖北 十堰 442060)
可靠性多学科优化在重型车车架设计中的应用研究
郝琪1,吕鹏2,吴胜军1,汪波3,吕钧3
(1.湖北汽车工业学院 汽车工程学院,湖北 十堰442002;2.湖南大学 机械与运载工程学院,湖南 长沙410205;3.十堰市精密制造有限公司,湖北 十堰442060)
摘要:文章选取车架生产中主要不确定量热轧钢板厚度为随机设计变量,基于Hammersly 采样法对40 t重型车主要承载构件车架进行静态强度、刚度和动态振动特性的多学科可靠性计算分析;结合多学科和可靠性优化理论,采用基于自适应面的SORA(sequential optimization and reliability assessment)可靠性单层循环优化方法对该车架进行基于可靠性的多学科优化设计,使得可靠度由原设计方案的50%左右提高到95%、车架质量减少2.3%。
关键词:车架;可靠度;多学科;SORA方法;Hammersly采样法
重型车的车架是主要承载部件,载荷大是其主要使用特点。传统的车架优化设计存在的问题如下:① 前期的优化设计基本属于车架不同性能学科的串行研究,割裂了多学科之间的相互作用,优化获得的往往是局部的最优解,很有可能失去全局最优解;② 前期研究基本为确定性优化设计,然而车架的大批量生产存在大量不容忽视的不确定因素,如材料参数的不确定性、结构尺寸的不确定性以及载荷条件的不确定性等,这些不确定因素往往将设计结果推向失效区域的边缘,设计变量的微小变动都有可能导致产品失效。
本文针对车架的主要性能指标(静态强度、刚度性能及动态一阶振动特性)进行多学科轻量化设计,综合考虑车架的可靠性优化设计问题。
1可靠性设计
1.1可靠性设计的基本定义及计算方法
单失效模态下结构的失效概率定义为:
(1)
其中,G(x)为结构功能函数;x={x1,x2,…,xn}为结构基本随机变量;fx(x)为随机变量x的联合概率密度函数。在系统概率密度函数已知且结构功能函数连续可导时,可靠度计算往往是一个多元函数多重积分问题。由于被积函数和积分边界比较复杂,用解析法或数值积分法求积分极为困难,由此发展了近似方法,如一阶可靠性计算方法(FORM)、二阶可靠性计算方法(SORM)和响应面法(RSM)等[1-4]。
对于大型复杂工程结构通常很难给出结构功能函数的显式表达,功能函数不能或不便求导,解决此类问题最直接的方法是采样统计法。应用采样统计产生系统性能的累积分布函数不受分布和性能函数的限制,如Monte Carlo模拟法、重要抽样模拟法等[5-6]。
1.2采样方法
在采样统计法中,采样方式是决定统计精度和效率的主要因素。随机采样(Monte Carlo法)在样本量巨大时是一种无偏估计[7],但其计算工作量太大,尤其是针对工程上的小概率失效问题,要得到精确的收敛结果,Monte Carlo法需要的抽样次数[8]为102~104,因此一般用作结构可靠性近似计算方法的结果校核和精度检验。
拉丁超立方(LH)采样能用较少的样本精确估计输出统计结果。它首先根据所需样本点的个数N,将m个随机设计变量的取值范围均划分成N个等概率无重复子区间,在每个子区间中按其概率分布随机选取一点,将m个随机设计变量的N个选取点随机组合。这种分层抽样的优点在于所选的随机变量数值能均匀地分布在各个随机变量的取样区间中,且考虑了随机变量的概率密度函数;但由于在m维空间采样点是随机组合的,因此m维空间的均匀性是该方法的局限[9]。
Hammersly采样基于r 进制小数构造最佳一致分布点集,均匀地在一个立方体中进行抽样,其优点在于可以用较少的样本提供对输出统计结果的可靠估计,相比于LH法,能在n维超立方体上取得很好的均匀分布。
LH法与Hammersly法采样点的对比如图1所示。本文采用Hammersly法进行采样分析。

图1 不同采样法的点集比较
2基于可靠性的多学科优化
2.1多学科优化
多学科设计优化(multidisciplinary design optimization,MDO)的实质是按照面向设计的思想集成各个学科的分析模型和工具,通过利用各个学科间的相互作用所产生的协同效应,以尽可能高的效率获得工程系统整体最优解,实现各个学科之间的并行设计[10]。MDO问题一般可以用非线性规划作如下数学描述:
min f(x,u(x));
(2)
其中,x为设计变量;u(x)为系统分析方程确定的状态方程;f(x,u(x))为目标函数;hj(x,u(x))为等式约束;gi(x,u(x))为不等式约束;N为多学科优化子系统的数目;S(x,u(x))为系统分析方程。多学科分析方程中的N个子系统方程确定了学科和交叉学科之间的耦合关系。
本文在车架优化设计时分别考虑了车架静态工况的强度、刚度以及车架动态振动特性2个学科的影响。各学科分析代码各异,多学科优化需要完成分析软件模块之间和学科组织系统与软件系统之间的数据接口的统一,在交互式计算过程中对耦合信息进行组织和管理。
2.2多学科可靠性优化
可靠性设计优化的数学模型为:
min f(xs,x,d);
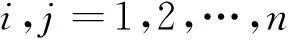
(3)
其中,f为目标函数;xs为确定性设计变量;x为不确定性设计变量;d为不确定设计变量x的数学期望;yij为学科i输出作为学科j输入的耦合变量;g为可靠性约束;n为学科数;k为概率约束个数。与单学科可靠性设计优化相比,多学科可靠性设计优化必须考虑学科间的耦合关系所带来的不确定性,即一个学科通过耦合变量传递到另一学科中的不确定性。
可靠性优化方法分为双循环方法和单循环方法[11-12]。双循环方法中,可靠性分析在优化循环中嵌套,每次优化迭代需执行多次可靠性分析来计算每个概率约束,其中可靠性计算占主体。单循环方法中,可靠性分析和优化分级执行,同时可以不断修正原始问题的约束,使其尽快接近要求的可靠性约束。本文采用计算效率较高的单循环SORA(sequential optimization and reliability assessment)方法。
2.3SORA 方法

min f(xs,x,d);
(4)

3重型车车架多学科可靠性优化
3.1原车架结构性能计算
某40 t重型自卸车为双后桥结构,前桥承载7 t,双后桥承载33 t,双后桥通过平衡悬架与车架横梁相连。此重型车车架由纵梁、纵梁加强板及6根横梁、横梁接头及横梁加强板组成,结构如图2所示。前桥安装于第2横梁和第3横梁之间,双后桥安装于第5横梁处,第5横梁由一对靠背槽钢、2层加强板及3层连接板构成。车架总长7.2 m、轴距4 m、轮距0.9 m、质量0.88 t,车架材料为厚度2.5~12.0 mm的低合金热轧大梁钢DL610,材料屈服应力大于550 MPa。

图2 车架结构
计算车架对应40 t满载工况强度和扭转刚度的2种静载工况,对于40 t满载、弯曲工况,将车架所承受的发动机、油箱等载荷简化为集中载荷作用于连接中心位置,载荷按前、后轴轴荷分配均布于车架。约束纵梁前悬前吊耳处3个平动自由度,后吊耳处约束除沿纵梁方向外的2个自由度[9];约束中、后桥平衡悬架连接处除沿纵梁方向外的2个自由度以及与平衡悬架底座连接处的垂向自由度。满载工况时最大Von Mises应力值243 MPa出现在飞机梁与平衡悬架连接处,静载安全系数为2.0~2.5,强度指标位于设计边缘;次大处出现在第2横梁连接处。扭转工况时,约束后悬连接处自由度,在前悬中心施加一对等值反向力,加载点加载方向上最大位移为3.74 mm,考虑轴距,扭转刚度为2.21×104N·m2/(°)。刚度值在同类车中处于标准水平[15]。车架的一阶频率为10.33 Hz,振型为一阶扭转,能避开8缸机的怠速激振频率。
3.2原车架的可靠性分析
车架的材料性能参数及材料尺寸为车架制造过程中带入的随机变量,根据文献[16],板料的实际厚度会偏离其公称厚度,热轧大梁钢厚度的制造误差在原尺寸的10%以内。本文以车架材料厚度尺寸为不确定变量,参考基本性能计算结果,为简化可靠性计算模型,选取影响车架性能的关键部件厚度t1、t2、t3、t4、t5为第2横梁接头、第2横梁、第5横梁、纵梁、纵深加强板厚度的不确定设计变量。由于钢板的厚度是独立变化的,可以认为不确定变量之间的相关性为0。
由于5个随机变量为多学科的共有设计变量,需要完成耦合代码的转换和相关性连接。通过提取不同工况设计变量,按对应的计算文件格式建立代码形成临时计算文件。同时,对各工况相同设计变量进行关联。
选取的随机变量服从正态分布,其分布特征的参数均值及标准差分别为(6.0,0.6)、(5.0,0.5)、(8.0,0.8)、(9.5,1.0)、(5.0,0.5)。建立强度、刚度、一阶频率3个结构功能响应函数,考虑原方案的安全域度不大,功能函数约束值取上述原车架计算对应的243 MPa、3.74 mm及10.33 Hz。采用Hammersly采样法,采样次数为100。通过采样统计,生成各响应的柱状图、概率密度函数(PDF)和累计分布函数(CDF)曲线如图3所示。

图3 3个响应的柱状图概率分布函数和累积分布函数
由图3可以看出,在应力响应的CDF图尾部仍有一定的上升趋势,较高应力区280 MPa以上仍有7频次出现,应力的均值在244 MPa附近,PDF图出现较长的平线段,没有明显的波峰,这说明强度的可靠度会有较大的波动;位移约束相对在低位移区出现频次较高,CDF图后部平缓,PDF图后端下降较明显,这对提高可靠度是有利的;CDF图上,频率响应表现为9.8 Hz以下的低频区上升相对较平缓,尾部高频区上升趋势较明显,有利于可靠度的提高,但PDF图出现2个波峰,分别在10.2 Hz和10.6 Hz附近,位于一阶频率10.33 Hz两侧,10 Hz以下相对频次较少。
原设计方案可靠度计算结果如图4所示,强度、刚度及频率约束的可靠度只有48%、57%、52%,由此可见厚度的波动极有可能引起车架的性能问题。

图4 不同响应的可靠度
3.3车架可靠性多学科优化
以轻量化为目标,先进行多学科确定性优化设计,仍取上述车架5个关键部件厚度为确定性设计变量,对应上述原车架强度、刚度、一阶频率3个性能响应参数值进行确定性多学科优化,设计变量的厚度值基本没有改变。由此可见,原车架基本性能之间的多学科协同轻量化设计结果较好。
在此基础上考虑可靠性对设计的影响,仍取车架5个原有厚度尺寸作为本次不确定性优化设计变量的均值,随机变量服从3.2节所述的正态分布,基于可靠性进行结构厚度参数的不确定性优化。采用基于自适应面的SORA可靠性优化算法,各学科约束可靠度为95%,根据(3)式,其多学科不确定性数学模型如(5)式,即
var(t1,t2,t3,t4,t5);
obj:min(m);
(5)
其中,目标函数车架质量m为5个不确定设计变量及其期望的函数。可靠性优化结果见表1所列。
由可靠性轻量化设计结果可知,5个随机设计变量中横梁5(飞机梁)及纵梁加强板厚度减小,自身尺寸较长的纵梁厚度增加,同时出现较大应力的第2横梁及接头厚度增加。通过设计变量厚度值的再设计,降低了应力、位移在设计区域范围内最大值,使得设计变量尺寸远离设计失效区。基于可靠性的优化设计与原设计相比,满载最大应力降低2.8%,扭转最大位移降低15.2%,一阶频率提高3.3%,可靠性提高到95%,且质量减少2.3%,较好地完成了可靠性轻量化设计的目标。

表1 可靠性优化结果
4结束语
本文通过Hammersly采样方法计算了原车架的可靠度,但可靠度不高,说明该车架及许多产品优化设计初期可靠性考虑得较少。
将可靠性分析引入车架的多学科优化设计中,对于没有明确极限状态函数的多学科不确定性分析,采用基于自适应面的SORA方法,提高了可靠性优化设计的效率,在保证可靠度的同时减轻了车架质量。该方法对于车架的前期综合设计有一定的指导作用。
[参考文献]
[1]Hasofer A M,Lind N C.Exact and invariant second-moment code format[J].Journal of the Engineering Mechanics Division,1974,100(1):111-121.
[2]Du X,Sudjianto A.First order saddlepoint approximation for reliability analysis[J].AIAA Journal,2004,42(6):1199-1207.
[3]冯世琪,廖林清,杨翔宇.非概率稳健可靠性理论及其发展趋势[J].重庆工学院学报:自然科学版,2007,21(2):45-50.
[4]Mahadevan S,Shi P.Multiple linearization method for nonlinear reliability analysis[J].Journal of Engineering Mechanics,2001,127(11):1165-1173.
[5]刘德顺,岳文辉,杜小平.不确定性分析与稳健设计的研究进展[J].中国机械工程,2006,17(17):1834-1841.
[6]梅刚.基于非线性随机有限元的结构可靠度问题研究[D].北京:清华大学,2005.
[7]Law A M,Kelton W D.Simulation modeling and analysis[M].New York:McGraw-Hill Company,1982:70-86.
[8]赵洁.机械可靠性分析的响应面法研究[D].西安:西北工业大学,2006.
[9]卓小君.改进Kriging模型及其在隧道围岩稳定可靠度计算中的应用[D].长沙:湖南大学,2011.
[10]范钦满,吴永海,徐诚.复杂产品设计与多学科设计优化综述[J].机械设计,2009,26(8):6-11.
[11]张代雨,宋保维,王鹏,等.两级系统多学科可靠性设计合成优化方法[J].西北工业大学学报,2012,30(6):808-813.
[12]刘云平,张俊,张冰,等.基于BLISS和PMA的多学科可靠性设计优化[J].航空学报,2013,34(10):2349-2356.
[13]陈仁伍,谷良贤,龚春林.一种基于SORA方法的多学科可靠性设计方法[J].机械强度,2008,30(1):37-40.
[14]夏青,蔡洪,张士峰.可靠性优化方法在飞航导弹多学科设计优化中的应用[J].弹箭与制导学报,2010,30(1):40-42.
[15]谷正气.轿车车身设计[M].北京:人民交通出版社,2002:461-462.
[16]GB/T 3273-2005,汽车大梁用热轧钢板和钢带[S].
(责任编辑胡亚敏)
Application of reliability-based multidisciplinary design optimization in heavy truck frame design
(1.Department of Automotive Engineeraing,College of Automotive Engineering,Hubei University of Automotive Technology,Shiyan 442002,China;2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410205,China;3.Shiyan Precision Manufacture Co.,Ltd.,Shiyan 442060,China)
Abstract:Taking the thickness of hot-rolled coil which is the main uncertain parameter in frame production as stochastic design variable,the multidisciplinary reliability of 40 t heavy truck frame is calculated by Hammersly sampling method in view of static strength,stiffness and dynamic vibration characteristic. The reliability of original frame is about 50%. Based on the multidisciplinary and reliability optimization theories,the frame is optimized by adopting single circulating sequential optimization and reliability assessment(SORA)method,and the reliability achieves 95% and the mass decreases 2.3%.
Key words:frame;reliability;multidisciplinarity;sequential optimization and reliability assessment(SORA)method;Hammersly sampling method
收稿日期:2015-02-27;修回日期:2015-06-30
基金项目:湖北省自然科学基金资助项目(2013CFA092)
作者简介:郝琪(1973-),女,山西祁县人,湖北汽车工业学院教授,硕士生导师.
doi:10.3969/j.issn.1003-5060.2016.06.004
中图分类号:U463
文献标识码:A
文章编号:1003-5060(2016)06-0736-05

