基于云遗传算法的关键链项目调度方法研究

周力，王杰

（东华大学　旭日工商管理学院，上海　20051）



基于云遗传算法的关键链项目调度方法研究

周力，王杰

（东华大学旭日工商管理学院，上海20051）

［摘要］针对资源约束下的项目调度问题，在前人研究的基础上，设计基于云模型的遗传算法用于求解关键链项目调度问题，利用调度问题库PSPLIB中标准实例j301_1验证算法的可行性。

［关键词］资源约束；关键链；项目调度；云遗传算法；PSPLIB

1　引言

关键链项目调度问题以资源约束项目调度问题为基础，是项目调度问题中的重要组成部分，该问题求解困难，多属于NP-hard问题，是项目管理学者研究的重点。

近年来，学者们设计了各种智能算法求解关键链项目调度问题。2006年，刘士新等提出了一种基于启发式规则的关键链调度方法；2013年，金敏力等在研究关键链项目调度的优化问题模型基础上，提出一种遗传算法求解单模式关键链项目调度问题；2014年，张琦、廖良才等提出一种自适应遗传算法对关键链项目调度模型进行求解。

本文在关键链项目管理思想的基础上，设计基于云模型的遗传算法求解单模式关键链项目调度问题，取调度问题库PSPLIB标准算例j301_1进行仿真试验，验证云遗传算法在求解关键链项目调度问题上的性能。

2　问题描述

本文在建立关键链优化调度问题模型时，采用以下问题简化方式。将问题分为三个阶段：①在以项目工期最短为调度目标时，不考虑非关键链上的输入缓冲区对工期的影响，考虑基于关键链上关键活动计算的项目缓冲区对项目工期的影响，寻找最优关键链；②基于关键链计算项目缓冲区，插入到项目结束活动之后；③采用刘士新等提出的方法，查找非关键链，并计算和插入输入缓冲区。

单执行模式资源受限项目优化调度问题的描述，如果同时考虑资源约束和活动工期的不确定性，那么该问题就转变为单模式关键链问题。

则可以建立基于关键链的单模式资源约束项目调度问题模型如下：

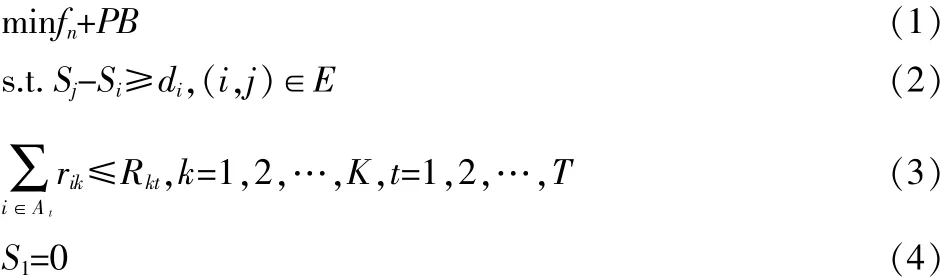
本文以标准问题库PSPLIB中问题j301_1项目为例，如表1所示。

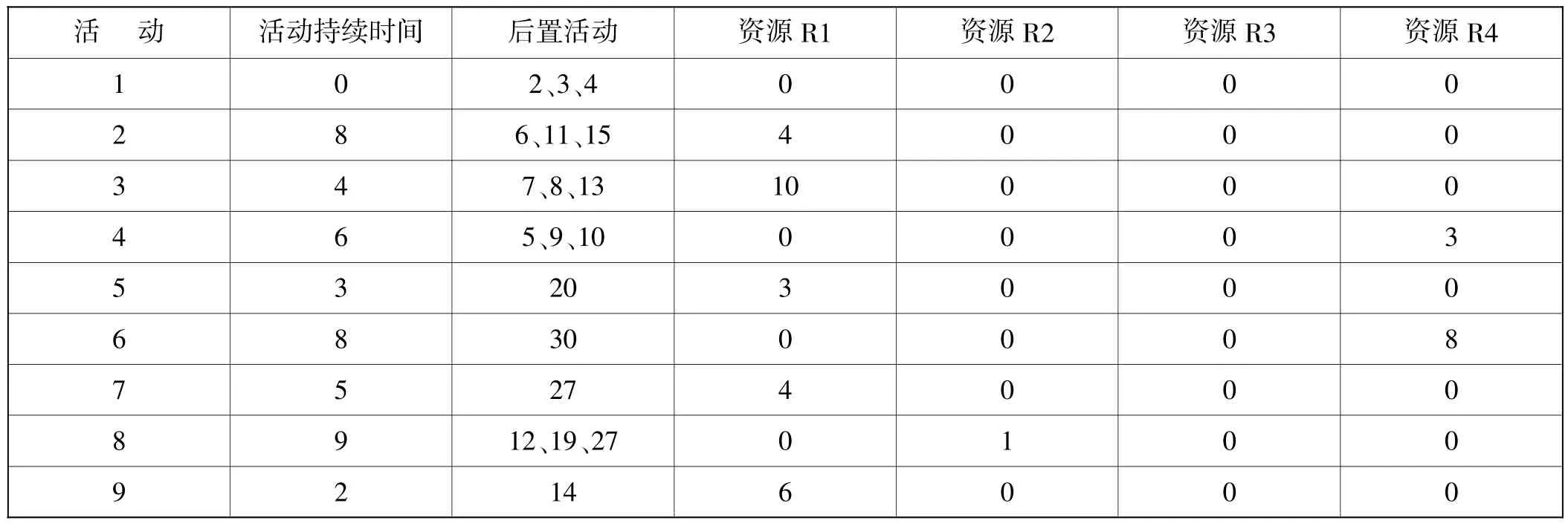
表1　项目实例表

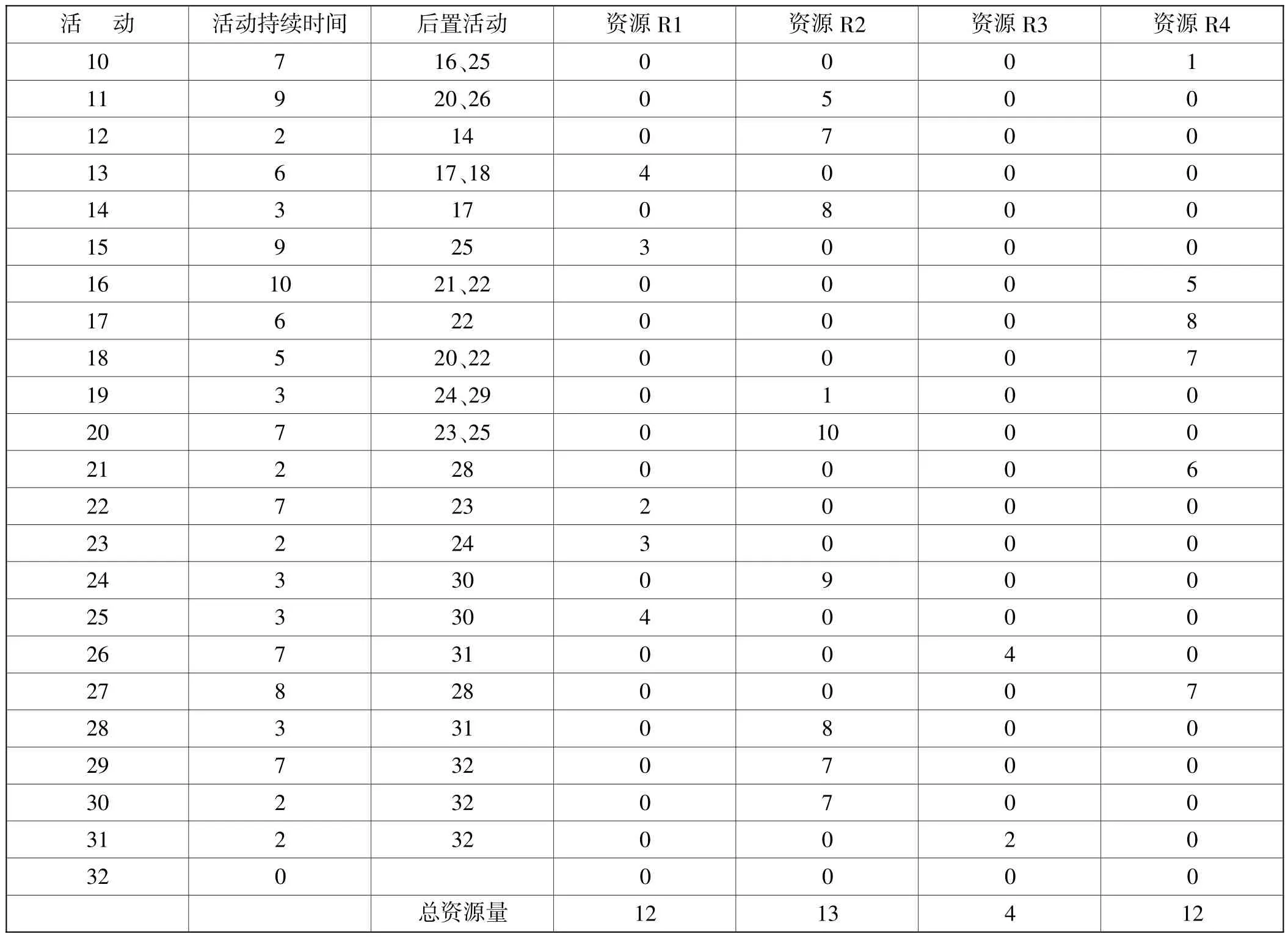
续表

3　云遗传算法设计

在云遗传算法中，把问题的解表示成“染色体”，首先给出可行的解，即初始种群，然后按照适者生存的自然进化法则，从中选择出适应值较高的个体，在新一代种群中再进行复制、交叉和变异，在新一代种群中按照相同的原则进行选择，直到进化到迭代代数为止。本文所采用的方式是利用最优保留和轮盘赌相结合的方式，在每一代种群中选择相对于种群规模的一定比例（10％）的最优个体直接进入到下一代中，这样既有利于最优个体的保留，也不破坏种群的多样性，更有利于产生更优秀的个体。同时采用父代和子代相互竞争的策略，在选择的过程中，子代与父代有相同的权利在轮盘赌的过程中被复制到下一代中。算法以识别单模式关键链为目标，随机生成初始种群，以迭代次数为终止条件，以适应度为评价准则。

3.1云遗传算法

对于一些改进的自适应遗传算法，其交叉概率和变异概率自适应于适应度，原理可以描述为：高于种群平均适应度的个体，随着其适应度的增加，为了对较优个体进行保护，交叉和变异概率逐渐减小；而低于种群平均适应度的个体采用最大交叉变异概率，使其产生较优个体。

云遗传算法结合遗传算法思想，沿用传统遗传算法的交叉、变异操作概念，由正态云模型的X条件云生成算法生成迭代过程中的交叉操作和变异概率。由于正态云模型具有随机性和稳定倾向性的特点，随机性可以保持个体多样性从而避免搜索陷入局部极值，而稳定倾向性又可以很好地保护较优个体从而对全局最值进行自适应定位。从而满足快速寻优的能力，并根据其随机性能避免陷入局部最优。其主要算法如下：

3.2适值函数与交叉变异操作

设i是当前种群第i个个体，F（i）是适应值函数，f（i）是第i个个体的目标值（即项目持续时间），fmax和fmin分别是当前种群的最大目标值和最小目标值。将目标值转化成适应值的转换公式如下：

式（7）中，C是属于［0，1］的正实数，在这里取0.5。

本文选择算子使用最优保持策略和轮盘赌方式结合的方式来产生下一代群体。把上一代群体中适应值最大的10％的个体不进行交叉和变异操作，而直接进入下一代群体中。另外的个体经云遗传算法的思想产生交叉和变异概率，通过pc和pm，选择参与交叉和变异的个体，通过交叉和变异操作生成下一代种群。

交叉操作选择随机地从父代1中选择若干个基因位置，将这些基因的值遗传给子代中相应的位置，子代中空缺的位置由父代2，由左到右，依次填补完整。通过变异算子使解空间向深度搜索。变异操作实质上是基于局部搜索的变异，对于一个染色体，随机产生一个基因，其邻域是确定的。变异算子随机产生在［1，n］内两个互异的整数i和j，交换这两个位置的基因信息，生成一个新的染色体。在一个种群的进化过程中由于变异产生部分个体。

4　算法比较与分析

由于初始种群是随机产生的。为了尽可能的消除不确定性，选取不同的种群规模，迭代次数进行仿真，对选用的j301_1的项目进行多次测试，以项目调度时间最短作为选择标准，选择最优个体作为比较对象。算法参数：种群规模取400和1 000，迭代次数为50。仿真结果如下：

当种群规模P=400，迭代次数n=50时，仿真结果如表2所示。当种群规模P=1 000，迭代次数n=50时，仿真结果如表3所示。

表2　种群规模4OO仿真结果表

表3　种群规模1 OOO仿真结果表

本文选取解的平均方差、最大方差、可行解比例三个指标来统计算法的有效性，结果如表4所示。

表4　j3O1_1测试表

由仿真结果得知，当迭代次数确定的时候，种群规模越大，平均方差越小，求解效果越好。当种群规模P=1 000时，求解效果最好。对应工作安排产生的最短工程时间为46，仿真结果如图1所示。

根据建立基于关键链的单模式资源约束项目调度问题模型Ftime=fn+PB即可求出项目调度时间Ftime。为了更好地理解云模型遗传算法去求解单执行模式关键链项目调度问题中的有效性和性能，本文选取调度问题库PSPLIB算例，分别与本文的遗传算法和其他智能算法（包括遗传算法等）进行比较。从仿真结果看，本文云遗传算法更有效（如表5所示）。

5　结语

在关键链项目管理思想基础上，设计云遗传算法求解单模式关键链项目调度问题，用标准问题库PSPLIB的问题进行求解，通过求解结果进行比较分析该算法的可行性、有效性和优越性。但是，关键链项目管理实施是一个非常复杂的过程，还需要考虑缓存机制、调整关键链等等一系列问题。同时多模式关键链项目调度问题也是需要研究的项目管理NP问题。

图1　云遗传算法仿真图

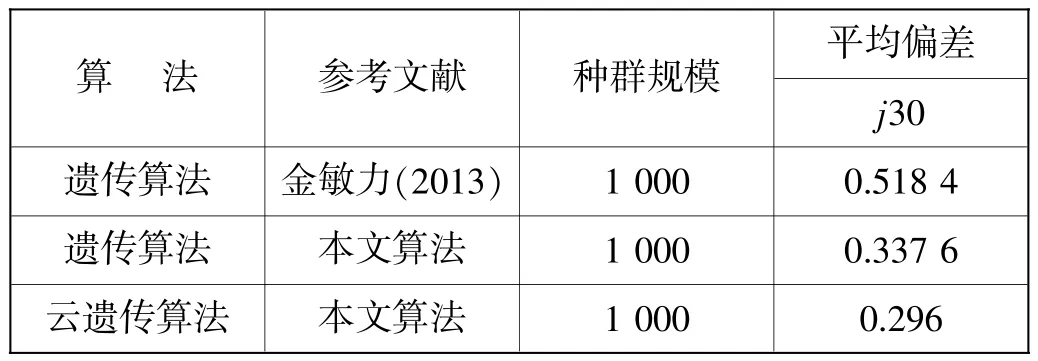
表5　仿真结果比较表

主要参考文献

［1］GoIdratt F M.CriticaI Chain［M］.Great Barrington：The North River Press PubIishing Corporation，1997.

［2］田文迪，崔南方.关键链项目管理中关键链和非关键链的识别［J］.工业工程与管理，2009，14（2）：88-93.

［3］李俊亭，王润孝，杨云涛.基于资源冲突调度的关键链项目进度研究［J］.西北工业大学学报.2010，28（4）：547-552.

［4］刘士新，宋健海，唐加福.资源受限项目调度中缓冲区的设定方法［J］.系统工程学报，2006，21（4）：381-386.

［5］刘娟.关键链单项目进度管理方法研究［D］.武汉：华中科技大学，2008.

［6］金敏力，冯玉强.遗传算法的关键链项目调度基准计划问题研究［J］.沈阳理工大学学报，2013，32（2）：12-17.

［7］张琦，廖良才，王卫威.基于改进遗传算法的关键链项目进度计划优化［J］.2014，24（4）：24-28.

［8］彭武良，王成恩.关键链项目调度模型及遗传算法求解［J］.系统工程学报，2010；25（1）：123-131.

［9］廖良才，张琦.基于混合遗传算法和关键链的多资源多项目进度计划优化［J］.科学技术与工程，2014，14（6）.

［10］李俊亭，王润孝，杨云涛.关键链多项目整体进度优化［J］.计算机集成制造系统，2011，17（8）：1772-1779.

［11］彭武良，金敏力，纪国焘.多模式关键链项目调度问题及其启发式求解［J］.计算机集成制造系统，2012，18（2）.

doi:10.3969/j.issn.1673 - 0194.2016.03.043

［中图分类号］TP301.6

［文献标识码］A

［文章编号］1673-0194（2016）03-0089-03

［收稿日期］2015-09-23