棒棒糖图的优美性

2016-07-16 07:12童细心

广东第二师范学院学报 2016年3期

童细心

(汕头职业技术学院自然科学系, 广东汕头 515041)

棒棒糖图的优美性

童细心

(汕头职业技术学院自然科学系, 广东汕头 515041)

摘要:给出了棒棒糖图Cn+Pl在n=4k,4k-1,4k+1时的优美标号，得到了棒棒糖图Cn+Pl在n=4k,4k-1,4k+1时是优美图的结论．

关键词:棒棒糖图；优美标号；优美图．

0引言

优美图是图论中一个十分有趣且重要的内容,它的提出始于1963年G.Ringel[1]的一个猜想,目前其研究成果已经被广泛应用于射电天文学、X-射线衍射晶体学、密码设计、通信网络编址、导弹控制码设计、同步机码设计、交通物流控制等领域,至今关于优美图的研究已得到了很多结果[1-8].由于缺乏一个系统和有力的工具,迄今,只能对一些特殊图探索其优美性.本文研究了棒棒糖图Cn+Pl的优美性,得到如下结论:

定理1当n=4k时,棒棒糖图Cn+Pl是优美图.

定理2当n=4k-1时,棒棒糖图Cn+Pl是优美图.

定理3当n=4k+1时,棒棒糖图Cn+Pl是优美图.

定义1[9]对于简单图G=(V,E),若∀v∈V,存在单射f(v)∈{0,1,2,…,|E|}(f(v)称为顶点v的标号),且导出的边标号g(e)=g(uv)=|f(u)-f(v)|是E到{1,2,3,…,|E|}的一个一一对应,则称图G是优美图,称f为图G的优美标号.

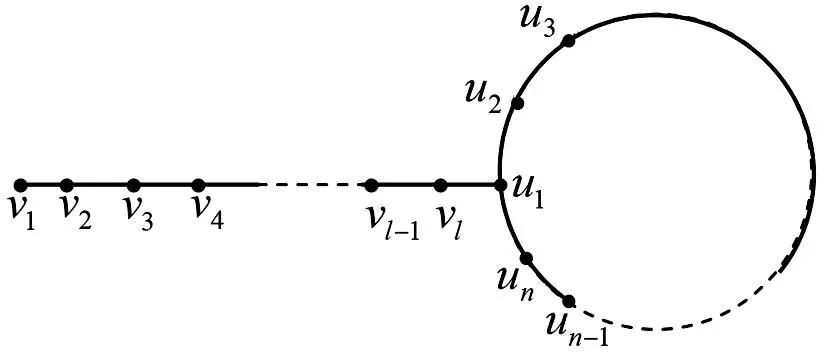
图1　棒棒糖图Cn+Pn

定义2[10]从圈Cn上的一个顶点ui悬挂一条长为l的路Pl所得到的图类,称为棒棒糖图,记为Cn+Pl.如图1所示,我们记圈Cn的顶点为ui,i=1,2,…,n.路Pl的顶点为vi,i=1,2,…,l.

本文所讨论的图均为无向简单图,v表示顶点v,uv表示以u,v为顶点的边,f(v)表示点v的标号,简记为v=f(v);同理,f(uv)表示边uv的标号,也简记为uv=f(uv).其他未加说明的定义和符号均来自文[11].

1定理1的证明

1.1情形1当n=4k,l=2t-1时,棒棒糖图Cn+Pl是优美图.

当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t-1,边数为n+l=4k+2t-1.给出棒棒糖图Cn+Pl的各顶点的标号递推算法A如下:

(ⅰ)v2i-1=i-1,i=1,2,…,t.

(ⅱ)v2i=4k+2t-i,i=1,2,…,t-1.

(ⅲ)u2i-1=4k+t-i+1,i=1,2,…,2k.

(ⅳ)u2i=t+i-1,i=1,2,…,k;u2i=t+i,i=k+1,k+2,…,2k.

按照算法A可得以下结果:

引理1当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-1}构成单射.

证明当n=4k,l=2t-1时,记M是棒棒糖图Cn+Pl的所有顶点标号集合,由算法A的(ⅰ)～(ⅳ)易知:

M1={v2i-1}={i-1|i=1,2,…,t}={0,1,…,t-1};

M2={v2i}={4k+2t-i|i=1,2,…,t-1}={4k+t+1,4k+t+2,…,4k+2t-1};

M3={u2i-1}={4k+t-i+1|i=1,2,…,2k}={2k+t+1,2k+t+2,…,4k+t};

M4={u2i}={t+i-1|i=1,2,…,k}∪{t+i|i=k+1,k+2,…,2k}=

{t,t+1,…,t+k-1}∪{t+k+1,t+k+2,…,t+2k}.

由此易验证,Mi∩Mj=∅,i≠j且i,j=1,2,3,4.即当n=4k,l=2t-1时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合M=M1∪M2∪M3∪M4中最小数是0(在M1中),最大数是4k+2t-1(在M2中),即当n=4k,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-1}构成单射.

引理2当n=4k,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-1}构成一一对应.

证明由算法A知,各顶点的标号最小为零,最大为4k+2t-1,故边的标号均不超过4k+2t-1.我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:4k+3≤v2i-1v2i≤4k+2t-1,其中i=1,2,…,t-1;4k+2≤v2iv2i+1≤4k+2t-2,其中i=1,2,…,t-1;v2t-1u1=4k+1.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅱ)易知,在圈u1u2…u4ku1中,边的标号范围为:2k+2≤u2i-1u2i≤4k,其中i=1,2,…,k;1≤u2i-1u2i≤2k-1,其中i=k+1,k+2,…,2k;2k+1≤u2iu2i+1≤4k-1,其中i=1,2,…,k;2≤u2iu2i+1≤2k-2,其中i=k+1,k+2,…,2k-1;u4ku1=2k.

由边的标号范围及奇偶性知,在圈u1u2…u4ku1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k,l=2t-1时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k,l=2t-1时, 棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-1}构成一一对应.

由引理1、引理2及定义1知,情形1成立,即当n=4k,l=2t-1时,棒棒糖图Cn+Pl是优美图.

1.2情形2当n=4k,l=2t时,棒棒糖图Cn+Pl是优美图.

当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t,边数为n+l=4k+2t.给出棒棒糖图Cn+Pl的各顶点的标号递推算法B如下:

(ⅰ)v2i-1=i-1,i=1,2,…,t.

(ⅱ)v2i=4k+2t-i+1,i=1,2,…,t.

(ⅲ)u2i-1=t+i-1,i=1,2,…,2k.

(ⅳ)u2i=4k+t-i+1,i=1,2,…,k;u2i=4k+t-i,i=k+1,k+2,…,2k.

按照算法B可得以下结果:

引理3当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t}构成单射.

证明当n=4k,l=2t时,记N是棒棒糖图Cn+Pl的所有顶点标号集合,由算法B的(ⅰ)～(ⅳ)易知:

N1={v2i-1}={i-1|i=1,2,…,t}={0,1,2,…,t-1};

N2={v2i}={4k+2t-i+1|i=1,2,…,t}={4k+t+1,4k+t+2,…,4k+2t};

N3={u2i-1}={t+i-1|i=1,2,…,2k}={t,t+1,…,t+2k-1};

N4={u2i}={4k+t-i+1|i=1,2,…,k}∪{4k+t-i|i=k+1,k+2,…,2k}=

{3k+t+1,3k+t+2,…,4k+t}∪{2k+t,2k+t+1,…,3k+t-1}.

由此易验证,Ni∩Nj=∅,i≠j且i,j=1,2,3,4.即当n=4k,l=2t时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合N=N1∪N2∪N3∪N4中最小数是0(在N1中),最大数是4k+2t(在N2中).即当n=4k,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t}构成单射.

引理4当n=4k,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t}构成一一对应.

证明由算法B知,各顶点的标号最小为零,最大为4k+2t,故边的标号均不超过4k+2t.我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:4k+2≤v2i-1v2i≤4k+2t,其中i=1,2,…,t;4k+3≤v2iv2i+1≤4k+2t-1,其中i=1,2,…,t-1;v2tu1=4k+1.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

由边的标号范围及奇偶性知,在圈u1u2…u4ku1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k,l=2t时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t}构成一一对应.

由引理3、引理4及定义1知,情形2成立,即当n=4k,l=2t时,棒棒糖图Cn+Pl是优美图.

定理1当n=4k时,棒棒糖图Cn+Pl是优美图.

证明由情形1、情形2可知,定理1成立.

2定理2的证明

2.1情形3当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl是优美图.

当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t-2,边数为n+l=4k+2t-2.此时给出棒棒糖图Cn+Pl的各顶点的标号递推算法C如下:

(ⅰ)v2i-1=i-1,i=1,2,…,t.

(ⅱ)v2i=4k+2t-i-1,i=1,2,…,t-1.

(ⅲ)u2i-1=4k+t-i,i=1,2,…,k;u2i-1=4k+t-i-1,i=k+1,k+2,…,2k.

(ⅳ)u2i=t+i-1,i=1,2,…,2k-1.

按照算法C可得以下结果:

引理5当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-2}构成单射.

证明当n=4k-1,l=2t-1时,记P是棒棒糖图Cn+Pl的所有顶点标号集合,由算法C的(ⅰ)～(ⅳ)易知:

P1={v2i-1}={i-1|i=1,2,…,t}={0,1,…,t-1};

P2={v2i}={4k+2t-i-1|i=1,2,…,t-1}={4k+t,4k+t+1,…,4k+2t-2};

P3={u2i-1}={4k+t-i|i=1,2,…,k}∪{4k+t-i-1|i=k+1,k+2,…,2k}=

{3k+t,3k+t+1,…,4k+t-1}∪{2k+t-1,2k+t,…,3k+t-2};

P4={u2i}={t+i-1|i=1,2,…,2k-1}={t,t+1,…,t+2k-2}.

由此易验证,Pi∩Pj=∅,i≠j且i,j=1,2,3,4.即当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合P=P1∪P2∪P3∪P4中最小数是0(在P1中),最大数是4k+2t-2(在P2中),即当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-2}构成单射.

引理6当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-2}构成一一对应.

证明由算法C知,各顶点的标号最小为零,最大为4k+2t-2,故边的标号均不超过4k+2t-2.由算法C知,我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:4k+2≤v2i-1v2i≤4k+2t-2,其中i=1,2,…,t-1;4k+1≤v2iv2i+1≤4k+2t-3,其中i=1,2,…,t-1;v2t-1u1=4k.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅱ)易知, 在圈u1u2…u4k-1u1中,边的标号范围为:2k+1≤u2i-1u2i≤4k-1,其中i=1,2,…,k;2≤u2i-1u2i≤2k-2,其中i=k+1,k+2,…,2k-1;2k+2≤u2iu2i+1≤4k-2,其中i=1,2,…,k-1;1≤u2iu2i+1≤2k-1,其中i=k,k+1,…,2k-1;u4k-1u1=2k.

由边的标号范围及奇偶性知,在圈u1u2…u4k-1u1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-2}构成一一对应.

由引理5、引理6及定义1知,情形3成立,即当n=4k-1,l=2t-1时,棒棒糖图Cn+Pl是优美图.

2.2情形4当n=4k-1,l=2t时,棒棒糖图Cn+Pl是优美图.

当n=4k-1,l=2t时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t-1,边数为n+l=4k+2t-1.此时给出棒棒糖图Cn+Pl的各顶点的标号递推算法D如下:

(ⅰ)v2i-1=i-1,i=1,2,…,t.

(ⅱ)v2i=4k+2t-i,i=1,2,…,t.

(ⅲ)u2i-1=t+i-1,i=1,2,…,k; u2i-1=t+i,i=k+1,k+2,…,2k.

(ⅳ)u2i=4k+t-i,i=1,2,…,2k-1.

按照算法D可得以下结果:

引理7当n=4k-1,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-1}构成单射.

证明当n=4k-1,l=2t时,记Q是棒棒糖图Cn+Pl的所有顶点标号集合,由算法D的(ⅰ)～(ⅳ)易知:

Q1={v2i-1}={i-1|i=1,2,…,t}={0,1,…,t-1};

Q2={v2i}={4k+2t-i|i=1,2,…,t}={4k+t,4k+t+1,…,4k+2t-1};

Q3={u2i-1}={t+i-1|i=1,2,…,k}∪{t+i|i=k+1,k+2,…,2k}=

{t,t+1,…,t+k-1}∪{t+k+1,t+k+2,…,t+2k};

Q4={u2i}={4k+t-i|i=1,2,…,2k-1}={2k+t+1,2k+t+2,…,4k+t-1}.

易验证,Qi∩Qj=∅,i≠j且i,j=1,2,3,4.即当n=4k-1,l=2t时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合Q=Q1∪Q2∪Q3∪Q4中最小数是0(在Q1中),最大数是4k+2t-1(在Q2中),即当n=4k-1,l=2t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t-1}构成单射.

引理8当n=4k-1,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-1}构成一一对应.

证明由算法D知,各顶点的标号中最小为零,最大为4k+2t-1,故边的标号均不超过4k+2t-1.由算法D知,我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:4k+1≤v2i-1v2i≤4k+2t-1,其中i=1,2,…,t;4k+2≤v2iv2i+1≤4k+2t-2,其中i=1,2,…,t-1;v2tu1=4k.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅱ)易知,在圈u1u2…u4k-1u1中,边的标号范围为:2k+1≤u2i-1u2i≤4k-1,其中i=1,2,…,k;2≤u2i-1u2i≤2k-2,其中i=k+1,k+2,…,2k-1;2k+2≤u2iu2i+1≤4k-2,其中i=1,2,…,k-1;1≤u2iu2i+1≤2k-1,其中i=k,k+1,…,2k-1;u4k-1u1=2k.

由边的标号范围及奇偶性知,在圈u1u2…u4k-1u1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k-1,l=2t时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k-1,l=2t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t-1}构成一一对应.

由引理7、引理8及定义1知,情形4成立,即当n=4k-1,l=2t时,棒棒糖图Cn+Pl是优美图.

定理2当n=4k-1时,棒棒糖图Cn+Pl是优美图.

证明由情形3、情形4可知,定理2成立.

3定理3的证明

3.1情形5当n=4k+1,l=2t-1时,棒棒糖图Cn+Pl是优美图.

当n=4k+1,l=2t-1时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t,边数为n+l=4k+2t.分k≥t和k

当k≥t时,

(ⅰ)v2i-1=2k+t+i-1,i=1,2,…,t.

(ⅱ)v2i=2k+t-i,i=1,2,…,t-1.

(ⅲ)u1=2k;u2i-1=4k+2t-i+2,i=2,3,…,k+t+1; u2i-1=4k+2t-i+1,i=k+t+2,k+t+3,…,2k+1.

(ⅳ)u2i=i-1,i=1,2,…,2k.

当k

(ⅴ)v2i-1=2k+t+i-1,i=1,2,…,k;v2i-1=2k+t+i,i=k+1,k+2,…,t.

(ⅵ)v2i=2k+t-i,i=1,2,…,t-1.

(ⅶ)u1=2k,u2i-1=4k+2t-i+2,i=2,3,…,2k+1.

(ⅷ)u2i=i-1,i=1,2,…,2k.

按照算法E可得以下结果:

引理9当n=4k+1,l=2t-1时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t}构成单射.

证明当n=4k+1,l=2t-1时,记R是棒棒糖图Cn+Pl的顶点标号集合.当k≥t时,由算法E的(ⅰ)～(ⅳ)易知:

R1={v2i-1}={2k+t+i-1|i=1,2,…,t}={2k+t,2k+t+1,…,2k+2t-1};

R2={v2i}={2k+t-i|i=1,2,…,t-1}={2k+1,2k+2,…,2k+t-1};

R3={u1}∪{u2i-1|i=2,3,…,k+t+1}∪{u2i-1|i=k+t+2,k+t+3,…,2k+1}=

{2k}∪{4k+2t-i+2|i=2,…,k+t+1}∪{4k+2t-i+1|i=k+t+2,…,2k+1}=

{2k}∪{3k+t+1,3k+t+2,…,4k+2t}∪{2k+2t,2k+2t+1,…,3k+t-1};

R4={u2i}={i-1|i=1,2,…,2k}={0,1,…,2k-1}.

当k

R1={v2i-1}={2k+t+i-1|i=1,2,…,k}∪{2k+t+i|i=k+1,k+2,…,t}=

{2k+t,2k+t+1,…,3k+t-1}∪{3k+t+1,3k+t+2,…,2k+2t};

R2={v2i}={2k+t-i|i=1,2,…,t-1}={2k+1,2k+2,…,2k+t-1};

R3={u1}∪{u2i-1|i=2,3,…,2k+1}={2k}∪{4k+2t-i+2|i=2,3,…,2k+1}=

{2k}∪{2k+2t+1,2k+2t+2,…,4k+2t};

R4={u2i}={i-1|i=1,2,…,2k}={0,1,…,2k-1}.

不论k≥t还是k

引理10当n=4k+1,l=2t-1时,n=4k+1,l=2t-1的边集与集合{1,2,3,…,4k+2t}构成一一对应.

证明由引理9知,各顶点的标号中最小为零,最大为4k+2t,故边的标号均不超过4k+2t.

当k≥t时,由算法E,我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:1≤v2i-1v2i≤2t-3,其中i=1,2,…,t-1;2≤v2iv2i+1≤2t-2,其中i=1,2,…,t-1;v2t-1u1=2t-1.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅱ)易知,在圈u1u2…u4k+1u1中,边的标号范围为:u1u2=2k;2k+1≤u2i-1u2i≤4k+2t-1,其中i=2,3,…,k+t+1;2t+2≤u2i-1u2i≤2k-2,其中i=k+t+2,…,2k;2k+2≤u2iu2i+1≤4k+2t,其中i=1,2,…,k+t;2t+1≤u2iu2i+1≤2k-1,其中i=k+t+1,…,2k;u4k+1u1=2t.

由边的标号范围及奇偶性知,在圈u1u2…u4k+1u1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.同理,当k

首先,由(Ⅲ)易知,在路v1v2…vlu1中,边的标号范围为:1≤v2i-1v2i≤2k-1,其中i=1,2,…,k;2k+2≤v2i-1v2i≤2t-2,其中i=k+1,k+2,…,t-1;2≤v2iv2i+1≤2k-2,其中i=1,2,…,k-1;2k+1≤v2iv2i+1≤2t-1,其中i=k,k+1,…,t-1;v2t-1u1=2t.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅳ)易知,在圈u1u2…u4k+1u1中,边的标号范围为:u1u2=2k;2t+3≤u2i-1u2i≤4k+2t-1,其中i=2,3,…,2k;2t+2≤u2iu2i+1≤4k+2t,其中i=1,2,…,2k;u4k+1u1=2t+1.

由边的标号范围及奇偶性知,在圈u1u2…u4k+1u1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k+1,l=2t-1时,不论k≥t还是k

由引理9、引理10及定义1知,情形5成立,即当n=4k+1,l=2t-1时,棒棒糖图Cn+Pl是优美图.

3.2情形6当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl是优美图．

当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl的顶点数为n+l=4k+2t+1,边数为n+l=4k+2t+1.给出棒棒糖图Cn+Pl的各顶点的标号递推算法F如下:

(ⅰ)v2i-1=2k+t-i+2,i=1,2,…,k; v2i-1=2k+t-i+1,i=k+1,k+2,…,t.

(ⅱ)v2i=2k+t+i+1,i=1,2,…,t.

(ⅲ)u1=2k;u2i-1=4k+2t-i+3,i=2,3,…,2k+1.

(ⅳ)u2i=i-1,i=1,2,…,2k.

按照算法F可得以下结果:

引理11当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t+1}构成单射.

证明当n=4k+1,l=2t且k≤t时,记S是棒棒糖图Cn+Pl的顶点标号集合,由算法F的(ⅰ)～(ⅳ)易知:

S1={v2i-1}={2k+t-i+2|i=1,2,…,k}∪{2k+t-i+1|i=k+1,k+2,…,2t}=

{k+t+2,k+t+3,…,2k+t+1}∪{2k+1,2k+2,…,k+t};

S2={v2i}={2k+t+i+1|i=1,2,…,t}={2k+t+2,2k+t+3,…,2k+2t+1};

S3={u2i-1}={u1}∪{u2i-1|i=2,3,…,2k+1}=

{2k}∪{4k+2t-i+3|i=2,3,…,2k+1}=

{2k}∪{2k+2t+2,2k+2t+3,…,4k+2t+1};

S4={u2i}={i-1|i=1,2,…,2k}={0,1,…,2k-1}.

易验证,Si∩Sj=∅,i≠j且i,j=1,2,3,4.即当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl中各顶点的标号均不相同.又所有顶点标号的集合S=S1∪S2∪S3∪S4中最小数是0(在S4中),最大数4k+2t+1(在S3中).所以,当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl的顶点集与集合{0,1,2,…,4k+2t+1}构成单射.

引理12当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t+1}构成一一对应.

证明由算法F知,各顶点的标号中最小为零,最大为4k+2t+1,故边的标号均不超过4k+2t+1.我们把边的标号分为两大类来考虑.

首先,由(Ⅰ)易知,在路v1v2…vlu1中,边的标号范围为:1≤v2i-1v2i≤2k-1,其中i=1,2,…,k;2k+2≤v2i-1v2i≤2t,其中i=k+1,k+2,…,t;2≤v2iv2i+1≤2k-2,其中i=1,2,…,k-1;2k+1≤v2iv2i+1≤2t-1,其中i=k,k+1,…,t-1;v2t-1u1=2t+1.

由边的标号范围及奇偶性知,在路v1v2…vlu1中各边的标号不相等.

其次,由(Ⅱ)易知,在圈u1u2…u4k+1u1中,边的标号范围为:u1u2=2k;2t+4≤u2i-1u2i≤4k+2t,其中i=2,3,…,2k;2t+3≤u2iu2i+1≤4k+2t+1,其中i=1,2,…,2k;u4k+1u1=2t+2.

由边的标号范围及奇偶性知,在圈u1u2…u4k+1u1中各边的标号不相等.

最后,由上易知,两类边的标号范围互不重叠,故也互不相等.

综上所述,当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl各边的标号均不相同.即当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl的边集与集合{1,2,3,…,4k+2t+1}构成一一对应.

由引理11、引理12及定义1知,情形6成立,即当n=4k+1,l=2t且k≤t时,棒棒糖图Cn+Pl是优美图.

定理3当n=4k+1时,棒棒糖图Cn+Pl是优美图.

证明由情形5、情形6及定义1可知,定理3成立.

参考文献：

[1]RINGELG.Problem25,in:theoryofgraphsanditsapplication[J].ProcSymposiumSmolenice, 1963,1263: 162-167.

[2]GALLIANJA.Adynamicsurveyofgraphlabeling[J].TheElectronicJournalofCombinatorics, 2009, 16(6): 6-27.

[5] 林育青.一类图的优美性[J].云南师范大学学报(自然科学版),2004,24(4):15-19.

[6] 林育青.Cn与1Cn的优美标号[J].安徽大学学报(自然科学版),2007,32(2):13-16.

[7] 张玲瑛,林育青,钟发胜,等.关于图2×Cn的标号[J].北华大学学报(自然科学版),2014,15(2):174-178.

[9] 马克杰.优美图[M].北京:北京大学出版社,1991：54-55.

[10] 陈暑波,夏方礼,龙韬，等.棒棒糖图的Merrifield-Simmons和Hosoya指数[J]. 湖南城市学院学报(自然科学版),2008,17(3):39-41.

[11]BANDYJA,MURTYUSR.Graphtheorywithapplication[M].NewYork:AmericanElsevierPublishingCoInc, 1976.

收稿日期：2015-10-11

基金项目:汕头职业技术学院2015年院级科研课题(SZK2015Y23).

作者简介:童细心,男,湖南岳阳人,汕头职业技术学院自然科学系讲师.

中图分类号：O157.5

文献标识码：A

文章编号：2095-3798(2016)03-0048-09

The Gracefulness of Lollipop Graphs

TONG Xi-xin

(Department of Natural Sciences, Shantou Polytechnic, Shantou, Guangdong, 515041, P.R.China)

Abstract:Graceful labeling algorithm of lollipop graphs Cn+Plare given when n=4k,4k-1,4k+1, and the conclusion is obtained that lollipop graphs Cn+Plare Graceful graph when n=4k,4k-1,4k+1.

Key words:lollipop graphs; graceful labeling; graceful graph

广东第二师范学院学报2016年3期

广东第二师范学院学报的其它文章: 基于OAuth 2.0扩展的访问控制委托架构; 基于医学生能力培养的创新型PBL教学模式探索与实践; 校园无线局域网非法接入及数据安全问题研究; 勿让信息技术遮蔽数学教师教学基本功; 高校学报女性编辑的 SWOT 分析及发展策略探讨