多属性双边匹配模型及其应用研究

段歆玮　詹文杰　杨　洁

(1. 华中科技大学管理学院； 2. 武汉纺织大学会计学院)



多属性双边匹配模型及其应用研究

段歆玮1詹文杰1杨洁2

(1. 华中科技大学管理学院； 2. 武汉纺织大学会计学院)

摘要：针对婚配问题中序数满意值信息无法衡量偏好强度关系，以及经典双边匹配Gale-Shapley算法只能求解男/女单方最优稳定解这两个问题，首先通过分析在线相亲网站上的会员信息，分别建立了男/女基数满意值的多属性评价模型，然后提出了基于满意值基数信息的双边匹配线性规划模型及其相应算法，最后通过一个算例比较了新算法与已有算法的差异。结果显示，所提出的新算法明显优于其他算法。

关键词：双边匹配； 婚配问题； 多属性决策； 满意度； 基数信息

随着“剩男剩女”的大量出现，男女婚配问题已经成为一个亟待解决的社会问题。在现实生活中，凡是涉及两组不同利益主体，每个主体尽量匹配到其满意的另一边主体，并使双方满意度最大，都属于双边匹配问题。男女婚配就是典型的双边匹配问题，除此之外，买方与卖方匹配、员工与岗位匹配、大学招生录取等问题都属于双边匹配的范畴[1]。通常，在双边匹配过程中，需要考虑双边主体的偏好信息。

目前，针对偏好序数信息的双边匹配问题的研究受到了国内外学者的关注[2～14]。GALE等[2]最早提出了稳定匹配的概念，并在男女双方对异性有着严格偏好序的条件下，给出了获取男方(或女方)最优稳定匹配解的Gale-Shapley算法(简称G-S算法)；MCVITE等[3]基于双边偏好序数信息提出了“Breakmarriage Operation”的递归算法，该算法可以求出双边匹配问题中全部稳定匹配解；ROTH[4,5]针对美国医学院毕业生和医院的双边匹配问题，在双方严格偏好序的条件下，给出了Hospital-Resident算法进行匹配；KNOBLAUCH[6]探讨了男女双方偏好序值信息随机分布情况下G-S算法的性质；MCVITE等[7]研究了男女双方人数不相等的婚姻匹配问题，并给出了求解该问题下的稳定匹配算法；VATE等[8]运用基于偏好序数信息，构建了一个线性规划模型来求解双方均衡的稳定双边匹配结果；樊治平等[9]和乐琦等[10]考虑双边主体的最高可接受偏好序，给出了一种严格双边匹配决策方法及其相应求解算法以及同时考虑整体序值和最大及中介收益最大情况下构建双边匹配模型。针对不完全偏好序数信息的双边匹配问题，MANLOVE等[11]给出了求解偏好信息不完全和序数信息不严格情况下的双边匹配问题的一种二次逼近算法；IWAMA等[12]探讨了同时在考虑双方主体不完全偏好信息以及序数不严格情形下，双边稳定匹配算法的复杂性；乐琦等[13]针对基于不完全序数信息的双边匹配问题，从完全双边匹配的视角提出了一种新的决策方法；梁海明等[14]在主体弱偏好序信息条件下，构建了同时考虑满意度和稳定性的双边匹配模型。

总之，现有的研究成果主要基于序数偏好信息和G-S算法及其改进。然而，基于序数偏好信息的做法，实质上假设主体对于匹配结果的满意程度与偏好序值呈逆线性关系，这在一些现实匹配问题中显得不尽合理[15]。因为序数偏好信息并不能反映男女双方满意程度的强度差异，偏好序值的增加(减少)与满意程度的降低(增加)之间不一定呈线性关系。例如，某男士对排名第1与排名第2的两位女士之间满意程度的差距可能要比排名第2和排名第3的两位女士之间的差距要大。此外，基于稳定匹配的G-S算法是从单边主体最优的视角提出的，即求解男方最优稳定解或女方最优稳定解，不能使匹配主体双方的满意程度都尽可能大[13]。有鉴于此，本研究首先通过分析在线相亲网站上的会员信息，分别建立了男/女基数满意值的多属性评价模型，然后提出了基于满意值基数信息的双边匹配线性规划模型及其相应算法。

1满意度评价指标体系

1.1评价指标及量化

近年来，有学者尝试把基数偏好信息引入双边匹配模型。樊治平等[15]认为序数偏好信息与主体满意值之间存在倒数关系，将序数信息转化为基数满意值，来求解双边匹配中的“既稳定，又满意”解；李铭洋等[16]将偏好序值信息转化为主体心理感知效用，建立双边匹配模型；QI[17]将语言评价信息转变为基数值，来求解双边匹配问题。与上述方法不同，本研究通过分析世纪佳缘网站上真实的会员信息，来获得婚配问题中的基数满意值信息。具体步骤如下：①通过指标的相关性分析及多指标综合评价加乘混合法，分别建立男/女满意度评价指标体系；②通过熵权法获得各指标权重；③通过比较主体的择偶条件与异性的自身条件之间的差异，得到每个主体在各项指标中的满意值以及整体满意值(详见下节)。

根据世纪佳缘网站会员的自身信息及择偶标准，本研究选取地区、年龄、身高、学历、民族、婚史状况等6个评价指标(见表1)。男女会员的注册信息构成如下4张表格：男性自身条件表(简称T1)；男性择偶条件表(简称T2)；女性自身条件表(简称T3)；女性择偶条件表(简称T4)。对于每一位男性来说，他对任意女性的满意值是该女性自身条件与其择偶条件的差值(即T3与T2的差值)，差值越小，表示女性越接近该男性的择偶条件，满意值也越高。同样，每位女性的满意值为男性自身条件与其择偶条件的差值(即T1与T4的差值)。

为了知道这6个指标对整体满意值的影响强度以及指标之间的组成关系，又从世纪佳缘网站上随机选取了男性和女性各500个样本作为研究对象，分别对男性/女性择偶条件表(T2/T4)中的6个指标进行相关性分析。在T2/T4表中，除了年龄和身高为区间型数值变量(相关性分析时取中值)外，其余4个指标均为字符型分类变量，需转化为数值型分类变量，具体处理方法见表1。

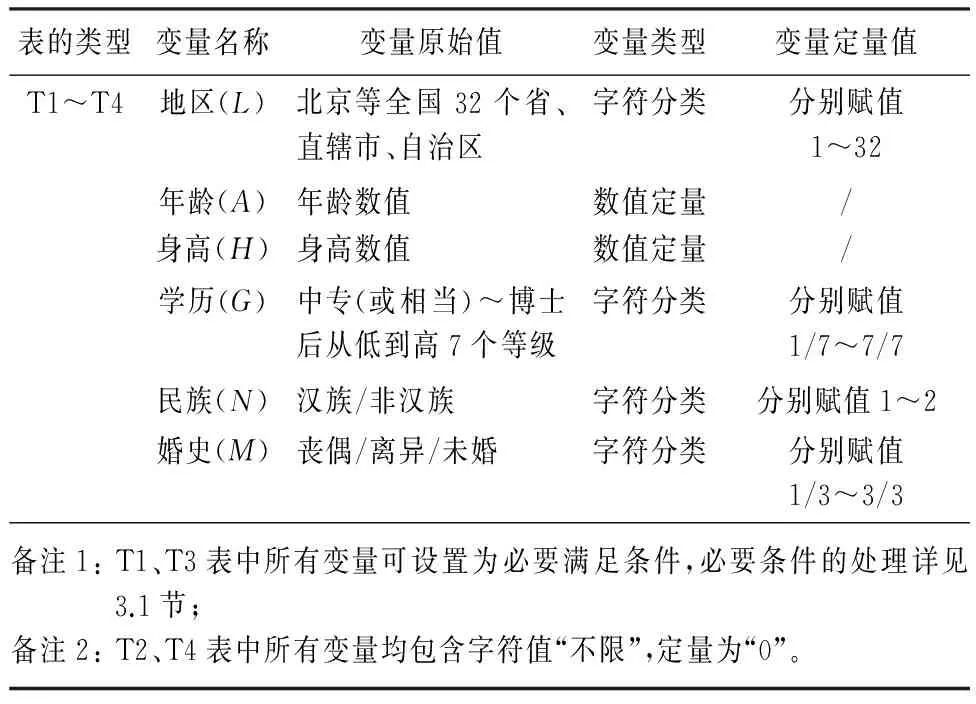
表1　指标定量处理

1.2男性择偶条件相关性分析

表2是对T2中6个指标进行相关性分析的结果。忽略相关性极弱或无相关(相关系数绝对值小于0.3)的相关关系，在男性择偶条件中，学历和婚史、民族和婚史之间在99%的置信区间上显著相关。

表2　男性样本择偶条件各指标相关性分析

注：**表示在0.01的显著水平上显著相关，下同。

根据多指标综合评价加乘混合法，本研究把相关性较为紧密的指标作为一类，做乘法处理，而把相关性不强的指标做加法处理，得到如下男性择偶满意度评价模型

(学历满意值×民族满意值×婚史满意值)，

(1)

式中，WML、WMA、WMH、WGGNM分别表示男性的地区、年龄、身高以及(学历×民族×婚史)的权重。然后，运用熵值法求出这4个权重值，分别是：WML= 0.248、WMA= 0.251、WMH=0.249、WMGNM= 0.252。

1.3女性择偶条件相关性分析

同理，表3是对T4中6个指标进行相关性分析的结果。研究发现，女性在进行择偶判断时，男性的年龄和身高、学历和婚史之间存在显著相关性，其余各指标之间相互独立。

表3　女性样本择偶条件各指标相关性分析

同样，根据多指标综合评价加乘混合法，得到如下女性择偶满意度评价模型

(2)

式中， WFL、WFAH、WFGM、WFN分别表示女性的地区、(年龄×身高)、(学历×婚史)以及民族的权重。然后，运用熵值法求出这4个权重值，分别是：WFL= 0.249，WFAH=0.249；WFGM=0.249，WFN= 0.253。

通过以上相关分析可以发现，男/女在择偶评价时存在显著差异：①对于年龄和身高两个生物属性指标，男性往往将它们单独考虑，而女性则放在一起考虑，说明女性比男性更强调生物指标的一致性，倾向于所谓“男才女貌”的理论解释；②对于学历、民族和婚史这3个社会属性指标，男性将它们一起考虑，而女性则单独考虑民族，说明男性在择偶时更强调异性社会属性的一致性，倾向于所谓“门当户对”的理论解释。

2满意度评价模型

2.1各项满意值计算

本研究计算各项满意值的基本思路是：通过比较男性(女性)的择偶条件与异性的自身条件之间的差异，即通过逐一比较T3与T2的6个指标的差值，得到每个男性对每个女性各项指标的满意值；同样，逐一比较T4与T1的6个指标的差值，得到每个女性对每个男性各项指标的满意值。但是，由于以上6个指标有的属于字符分类变量，有的属于区间数值变量，因此本研究采用如下处理方法来具体计算各项指标的满意值。下面以计算第i个男性(表示为Mi)对第j个女性(表示为Fj)的满意值为例，具体计算方法如下。

(1)地区满意值由表1可知，原始的字符型地区变量转化为1～32分类变量，分别代表我国32个省、直辖市、自治区。如果男性(或女性)在其择偶需求条件中不限地区，则变量取值为0。令LMi_T2表示男性择偶条件中的地区需求变量，LFj_T3表示女性自身条件中的地区变量，SLMi2Fj表示i男性对j女性的地区满意值，其计算方法见式(3)。具体如下：如果i男性在择偶需求条件中不限地区(即LMi_T2=0)，则无论LFj_T3的取值多少，该男性的满意值始终为1；如果LFj_T3=LMi_T2，表明j女性满足i男性的地区需求，则其满意值为1；如果LMi_T2≠0且LFj_T2≠LMi_T3，表明j女性不满足i男性的地区需求，则其满意值为0.5；如果i男性设定择偶条件地区需求为必要指标且LFj_T2≠LMi_T3，则对应地区满意值为0。由此可见，地区满意值取值范围为[0, 1]

(3)

(2)年龄满意值令[LAMi_T2,RAMi_T2]为男性择偶条件中的年龄需求区间，LO_AMi和UP_AMi分别表示该男性可以接受的女性年龄下限和上限，SAMi2Fj表示i男性对j女性的年龄满意值，其计算方法见式(4)。如果AFj_T3[LAMi_T2,RAMi_T2]，其满意值为1；如果AFj_T3(LO_AMi,LAMi_T2)或AFj_T3(RAMi_T2,UP_AMi)，满意值均在区间范围内呈线性变化；如果AFj_T3≤LO_AMi或AFj_T3≥UP_AMi，其满意值均为0；如果i男性设定择偶条件年龄需求为必要指标，且AFj_T3∉[LAMi_T2,RAMi_T2]，则对应年龄满意值为0

SAMi2Fj=

(4)

(3)身高满意值令[LHMi_T2,RHMi_T2]表示男性择偶条件中的身高需求区间，LO_HMi和UP_HMi分别表示该男性可以接受的女性身高下限和上限，SHMi2Fj表示i男性对j女性的身高满意值，具体计算方式与年龄满意值计算方式相似

SHMi2Fj=

(5)

(4)学历满意值由表1可知，原始的学历变量转化为1/7～7/7分类变量，由低到高分别表示中专(或相当学历)至博士后。如果不限学历，则该变量为0/7。令GMi_T2表示男性择偶条件中的学历需求下限，GFj_T3表示女性自身条件中的学历变量，SGMi2Fj表示i男性对j女性的学历满意值，其计算方法为

(6)

如果该男性认为女性学历为非必要条件，则满意值为女性自身学历与男性择偶需求差值(如果女性达到男性学历要求的下限，其学历满意值为负)；如果学历为必要条件且女性学历低于男性需求，则其对该女性学历的满意值为-6/7(=1/7-7/7。即学历满意值最差条件是女性自身学历为1/7，而男性需求条件为7/7)；如果学历为必要条件且女性学历达到男性需求下限，则满意值为女性自身学历与男性择偶需求差值。由此可见，学历满意值取值范围为[-6/7, 1]。

(5)民族满意值令NMi_T2表示男性择偶条件中的民族需求变量，NFj_T3表示女性自身条件中的民族变量，SNMi2Fj表示i男性对j女性的民族满意值，具体计算方式与地区满意值计算方式相似

(7)

(6)婚史满意值由表1可知，原始的婚史变量转化为1/3～3/3分类变量，由低到高分别表示丧偶、离异和未婚。令，GMi_T2表示男性择偶条件中的婚史需求下限，GFj_T3表示女性自身条件中的婚史变量，SGMi2Fj表示i男性对j女性的婚史满意值，其计算方法与学历满意值类似

(8)

婚史满意值取值范围为[-2/3, 1]。类似的，可以分别得到j女性对i男性的各项指标满意值。

2.2整体满意值计算及其归一化

假设参与婚配的男性的个数为NM(1≤i≤NM)，女性的个数为NF(1≤j≤NF)。首先，根据式(3)～式(8)分别计算得到i男性对j女性的各项指标满意值，然后根据式(1)分别求出i男性对每个女性的整体满意值

SMi2Fj=0.248SLMi2Fj+0.251SAMi2Fj+0.249SHMi2Fj+

(9)

(10)

类似的，首先仿照式(3)～式(8)分别计算得到j女性对i(1≤i≤NM)男性的各项指标满意值，然后根据式(2)分别求出j女性对每个男性(1≤i≤NM)的整体满意值

SFj2Mi=0.249SLFj2Mi+0.249(SAFj2MiSHFj2Mi)+

(11)

最后，分别找出j女性最满意和最不满意的男性，仿照式(10)对每个男性(1≤ i ≤NM)的整体满意值进行归一化处理。处理过后的满意值也转化为j女性对每个男性的满意值百分比。

3双边匹配模型

3.1模型建立

以男性和女性整体平均满意程度为目标建立双边匹配模型

(12)

在模型中，式(12)为目标函数，由男性平均满意程度与女性平均满意程度组成，其含义为尽可能使男女性平均满意程度最大。变量kij为决策变量，取值0或1，表示 i男性与j女性是否进行匹配。约束(13-1)、(13-2)、(13-3)、(13-4)均为匹配约束，分别规定一名男性最多只能匹配一名女性，一名女性也最多只能匹配一名男性，最终匹配数量为min(NM,NF)。约束(13-5)为稳定性约束，规定在得到的匹配解中，不存在不稳定情况，即任意两组匹配解(i男-j女；i′男-j′女)，i男对j′女的满意度以及j′女对i男的满意度不可能同时高于他们对现有对象的满意度；i′男对j女的满意度以及j女对i′男的满意度也不可能同时高于他们对现有对象的满意度。

3.2模型求解

由于上述匹配模型的目标函数和约束条件均为线性，所以匹配模型是线性规划问题，本研究采用C++编译程序求解该模型，算法的伪代码见图1。

设置 循环总数当time从1到循环总数循环随机匹配NM:NF名对象对于每一个男性i:如果他已匹配女性j 搜索所有其余女性j'如果女性j已匹配男性i'如果 (SMi2Fj

4算例分析

本研究从前面500个男/女会员中，随机选取了50名男性和50名女性进行匹配。令男/女性择偶需求条件可接受年龄下限LO_AMi=80%LAMi_T2，上限UP_AMi=120%RAMi_T2；可接受身高下限LO_HMi=95%LHMi_T2，上限UP_HMi=105%RHMi_T2。首先，根据男/女满意度评价模型，分别计算这50名男会员和50名女会员各自对异性的满意值百分比；然后，采用本研究提出的基数线性规划模型求解，并与其他算法的结果进行对比。需要说明的是，其他算法中只要求满意值的序数信息，本研究根据基数满意值百分比的大小进行了相应排序。

表4给出了基数线性规划模型与经典G-S算法的最终匹配结果，其中Fj列中的第1个数字表示基数线性规划模型中相应男性匹配的女性编号；第2个数字表示G-S算法中男方表白获得的与之匹配的女性编号(即man-optimal)；第3个数字表示G-S算法中女方表白获得的与该男性匹配的女性编号(即woman-optimal)。从表4中可以看出，不同的算法所得到的匹配结果有明显差异。例如，男1在基数线性规划模型下的匹配结果是女21，而在G-S算法下的匹配结果分别是女46(man-optimal)和女49(woman-optimal)；以此类推*在基于序数的匹配算法中，当满意值相同时本研究采取了随机排序，可能导致匹配结果的略微区别，因此表4中只给出了其中一种匹配结果，而图2给出了10次求解的平均满意值。。

表4　基数线性规划模型与G-S算法匹配结果

图2给出了本研究算法与其他算法在平均满意值方面的差异，可以看出：基数线性规划模型计算出来的匹配结果的平均满意值是最高的，超过0.85；其次，是序数线性规划模型，平均满意值在0.75附近波动；接下来，是樊治平等[15]提出一种将序数信息求倒数从而获得简单基数信息的算法(简称“樊治平模型”)，平均满意值在0.68～0.72区间波动；最后是经典G-S算法，其满意值在0.5～0.652区间波动。

图1　基数、序数线性规划模型与G-S算法、　　樊治平模型的平均满意值对比

5结论

本研究通过对在线相亲网站的会员信息数据分析，分别构建了男/女择偶满意度评价模型，并提出了基于满意值基数信息的双边匹配线性规划模型及其相应算法。研究结果显示，该方法在保证稳定匹配的条件下，整体满意度水平达到85%以上，在整体满意值和匹配结果的稳定性方面均优于已有算法。此外，本研究还发现男/女性择偶价值观念存在显著差异，男性较女性更强调社会属性的一致性，而女性较男性则更强调生物属性的一致性。

理论方面，本研究提出的基于基数信息的双边匹配模型和算法，弥补了基于序数信息的匹配算法中满意度为序数信息无法衡量偏好强度关系的缺点，丰富和发展了双边匹配模型。应用方面，婚姻中介可以利用此模型为约会双方事先安排好匹配对象，从而节约时间和提高匹配成功率；另外，该算法还可以应用到其他多属性双边匹配问题，如学校与新生的匹配、公司与员工的匹配、电子中介下的买卖双方的匹配等。

本研究也存在一些不足，需要在今后的研究中逐步完善：①受在数据来源以及量化方面的制约，本研究的满意度评价指标模型只考虑了6个因素，在后续的研究中，可以适当增加其他因素(如相貌、性格等)；②今后还可以和相关相亲网站合作，用真实的相亲匹配结果数据来进一步检验本研究模型的有效性。

参考文献

[1] 陈希, 樊治平. 双边匹配决策的研究现状与展望[J]. 管理评论, 2012, 24(1): 57～63

[2] GALE D, SHAPLEY L S. College Admissions and the Stability of Marriage[J]. The American Mathematical Minthly, 1962, 69(1): 9～15

[3] MCVITE D G, WILSON L B. The Stable Marriage Problem[J]. Communications of the Association for Computing Machinery, 1971, 14(7): 486～492

[4] ROTH A E. On the Allocation of Residents to Rural Hospitals: A General Property of Two-Sided Matching Markets[J]. Econometrica, 1986, 54(2): 425～427

[5] ROTH A E. Common and Confictiong Interests in Two-Sided Matching Markets[J]. European Economic Review, 1985, 27(1): 75～96

[6] KNOBLAUCH V. Marriage Matching and Gender Satisfaction[J]. Social Choice and Welfare, 2009, 32(1): 15～27

[7] MCVITE D G, WILSON L B. Stable Marriage Assignment for Unequal Sets[J]. Bit Numerical mathematics, 1970, 10(3): 295～309

[8] VATE V, JOHN H. Linear Programming Brings Marital Bliss[J]. Operations Research Letters, 1989, 8(3): 1～23

[9] 樊治平, 乐琦. 基于完全偏好序信息的严格双边匹配方法[J]. 管理科学学报, 2014, 17(1): 21～34

[10] 乐琦, 樊治平. 基于不完全序值信息的双边匹配决策方法[J]. 管理科学学报, 2015, 18(2): 23～35

[11] MANLOVE D F, IRVING R W, IWAMA K, et al. Hard Variants of Stable Marriage[J]. Theoretical Computer Science, 2002, 276(1/2): 261～279

[12] IWAMA K, MANLOVE D, MIYAZAKI S, et al. Stable Marriage with Incomplete Lists and Ties[C]//GIORGIO A, MARIANGIOLA D C, SIMONETHA R. Proceedings ICALP’ 99: The 26thInternational Colloquium on Automata, Languages, and Programming, Lecture Notes in Computer Science, Springer, Berlin, 1999, 1 644: 443～452

[13] 乐琦, 樊治平. 一种具有序值信息的双边匹配决策方法[J]. 系统工程学报, 2012, 27(2): 185～192

[14] 梁海明, 姜艳萍. 一种考虑中介交易态度的买卖双边匹配决策方法[J]. 运筹与管理, 2013, 22(5): 128～133

[15] 樊治平, 李铭洋, 乐琦. 考虑稳定匹配条件的双边满意匹配决策方法[J]. 中国管理科学, 2014, 22(4): 112～118

[16] 李铭洋, 樊治平, 乐琦. 考虑双方主体心理行为的稳定双边匹配方法[J]. 系统工程理论与实践, 2014, 34(10): 2 591～2 599

[17] QI Y. Two-Sided Matching Decision with Two-Granularity Uncertain and Incomplete Linguistic Terms[J]. International Journal of Multimedia & Ubiquitous Engineering, 2015, 10(2): 121～127

(编辑刘继宁)

Research of Marriage Matching Problem Based on Multiple-Attribute Two-Sided Matching Model

DUAN Xinwei1ZHAN Wenjie1YANG Jie2

(1. Huazhong University of Science and Technology, Wuhan, China;2. Wuhan Textile University, Wuhan, China)

Abstract：The ordinal information of satisfaction using in the marriage matching cannot measure the intensity of the preferences, and the classic Gale-Shapley algorithm can get one-sided optimal matching result only, i.e. man-optimal or woman-optimal. According to the above defects, this study firstly comes up with two cardinal satisfaction evaluation models for male and female respectively by analyzing the members data from an online dating website. Then, a linear programming model and its solution are given to solve the two-sided matching problem based on the cardinal satisfaction. Finally, a numerical example is presented to illustrate the feasibility and validity of the new model. It is found that the result is significantly better than that of other algorithms under the condition of stable matching.

Key words：two-sided matching; marriage problem; multiple-attribute decision making; degree of satisfaction; cardinal information

作者简介：KANJANA JANSUKPUM(1978～)，女，泰国人。武汉大学(武汉市430072)信息管理学院博士研究生。研究方向为旅游电子商务。E-mail：kanjana@whu.edu.cn

DOI编码：10.3969/j.issn.1672-884x.2016.06.013

收稿日期：2016-01-19

基金项目：湖北省人文社会科学重点研究基地资助项目(2013WZ005)

中图法分类号：C93

文献标志码：A

文章编号：1672-884X(2016)06-0899-07