辅助线在几何题中的重要性
赵利侠


摘 要: 几何是初中教学的一门重要学科,然而学生在几何证题的证明与计算时总是受到阻碍,此时若是解题思路顺畅就需要科学合理地添加必要的辅助线.辅助线在几何题的解答中起到了至关重要的作用,其主要表现在三个方面:第一,它作为解决问题的桥梁可以将已知与未知巧妙地联系在一起;第二,为了利用图形性质解题它将分散的条件集中化从而构成简单基本的图形;第三,它可以为几何体的解证创造条件使其隐藏着的条件明朗化从而促进解题顺利进行.
关键词: 初中几何教学 辅助线 几何题 重要性
如何作辅助线,在初中数学课程讲解中,是解证几何题中的一个非常重要的知识点.而在解证几何题时所作辅助线的优劣则影响了证明过程的难易程度.辅助线在平面几何图形中的添加,不仅要求学生熟练掌握各个图形的特征及性质,还要求学生有一定的思维创造性.因此科学正确地在几何证题中作出辅助线有一定的难度.
一、作辅助线的思路
在几何教学中,辅助线的添设对几何题的解答起着至关重要的作用,而如何巧设辅助线是解题中必不可少的一个条件.由于综合法和分析法是证明几何题时用到的两种基本方法.因此,在作辅助线时便有了两条思路可供选择,第一条是从综合法的方面考虑作辅助线.在使用综合法证题时,由于通过已知条件推证结论而思路受到阻断,此时便可以根据图形的特征巧妙地添加辅助线,从而利用图形特有的性质为后续推证提供便利.第二条是从分析法的方面考虑来作辅助线.而使用分析法的证题,则是从结论逆推条件,当形成结论的条件在推理中受到阻碍时可添设恰当的辅助线,从而使这一过程继续进行下去.无论是从命题给出的已知条件还是结论作分析时都应该结合图形的特点完成,不同的图形特点所要添设的辅助线位置也是不一样的,而正确位置的辅助线有利于我们快速简便地完成解题.
二、例题分析辅助线的重要性
(一)构建桥梁
例1:如图1所示,∠EOA=∠EOB=15°,EF∥OB,EC⊥OB,若CE=1,则EF=?
在解答这一试题时我们先要对题目进行分析:从已知的条件可以得出∠AOB=30°,那么此题的考点将与30度角的直角三角形的性质有关,∠EOA=∠EOB=15°那么就涉及了角平分线相关的问题,EF∥OB则涉及了平行的性质.要想求出EF=?,根据已知的条件不足以求解,那么此时就需要考虑巧设辅助线解答了.
解:过点E作EG⊥OA交于AF,
因为EF∥OB,所以∠OEF=∠COE=15°,
又因为∠EOA=15°,所以∠EFG=15°+15°=30°.
因为OE平分∠AOB,EC⊥OB,所以EG=EC=1,
所以EF=2EG=2×1=2
答:EF的长为2.
(二)简化图形
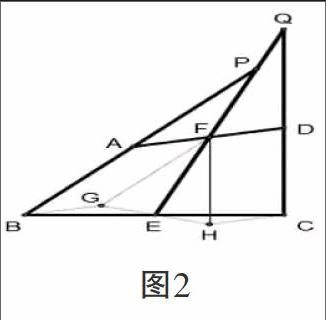
例2:如图2所示,已知在四边形ABCD中,AB=CD,点F和E分别为AD、BC边上的中点,延长BA、CD,分别交EF的延长线于P、Q,求证:∠APF=∠DQF
此题为求证性试题,已知结论的存在,对结论通过给出的条件做证明.而本题中与证明结论存在有关的条件较分散.因此需考虑到作辅助线的方法使已知条件做集中化处理,以此方便证题.
证明:如上图所示,过点F分别作FG∥AB,FH∥DC,过点B作BG∥AD交FG于点G,过点C作CH∥AD交FH于点H,连接GE与HE.
已知:FG∥AB,BG∥AD,得出四边形FGBA为平行四边形,
所以:FG=AB,FA=GB.
又因:FH∥DC,CH∥AD,得出四边形CDFH也为平行四边形,
所以:DF=CH,DC=FH.
因为:点F和E分别为AD、BC边上的中点且AB=CD
所以:FA=FD,EB=EC,FG=FH,则:GB=HC.
因为:BG∥AD,CH∥AD,则:BG∥CH.
所以:∠GBE=∠HCE,得出△BGE≌△CHE.
所以:GE=HE,则:△FGE≌△FHE(SSS).
所以:∠EFG=∠EFH.
因为:FG∥AB,得出:∠GFE=∠APF
又因:FH∥DC,得出:∠Q=∠EFH
所以:∠APF=∠DQF.
(三)明朗化隐含条件
例3:如图3所示,在△ABC中,BD、CE分别是AC、AB边上的高,M、N分别是DE、BC的中点,求证:MN⊥DE.
在分析这一证明题时我们可以得出其中隐含了中线在直角三角形斜边上的性质,为了将隐含的条件转化为直接条件,那么此时就必须考虑使用添设辅助线进行解证.
证明:连接NE与ND
已知:点N是BC的中点,BD、CE分别是AC、AB边上的高
所以:NE是Rt△BCE斜边上的中线
ND是Rt△BCD斜边上的中线
所以:根据直角三角形斜边上中线的性质得出NE=1/2BC,ND=1/2BC
所以:根据等量代换得出NE=ND
又因:点M是ED的中点
所以:根据等腰三角形三线合一的性质得出MN⊥DE
三、结语
在几何证题中辅助线的添加没有法则能够遵循,其添设方法因题而定.学生要通过作好辅助线提高解证几何题的能力就必须在平时练习中仔细分析,反复探究,不断地积累解题经验并做好总结.
参考文献:
[1]德力根仓.浅谈辅助线在几何证题中的应用[J].赤峰学院学报,2014(30).
[2]李淑华.浅谈辅助线在几何证题中的作用[J].承德民族师专学报,2009(29).
[3]李春英.谈平面几何辅助线的添加[J].新课程,2015(1).

