基于复杂网络的交互效应下多项目组合风险优化研究

王重阳，郑唯唯，刘　晨

(西安工程大学 理学院，陕西 西安　710048)



基于复杂网络的交互效应下多项目组合风险优化研究

王重阳，郑唯唯*，刘晨

(西安工程大学 理学院，陕西 西安710048)

摘要：针对区间形态的交互效应多项目组合风险优化问题，运用复杂网络统计特征分析多项目组合中各项目的重要性及在组合网络中的地位，依据项目的成功概率与对其余项目成功概率的贡献量对组合进行优化，构建交互效应下区间型多项目组合风险优化模型；并根据算法流程，利用复杂网络软件Gephi以及Matlab编程，提高了算法运行效率，并通过实验验证方法的有效性.

关键词：项目组合风险；交互效应；复杂网络理论

0引言

自1975年，Baker和Freeland[1]首次提出项目间存在交互效应的影响；1993年，Schmidt[2]系统的提出了项目间基于资源、技术以及收益的交互关系，并将其定量融合在项目组合选择模型.之后，关于交互效应对项目组合风险、收益及成本的影响逐渐引起了研究者的重视.文献[3,4]研究了在交互效应影响下，项目组合风险的度量及优化问题；文献[5-8]基于交互效应视角，研究了项目的最优组合选择问题.但现有关于项目组合交互效应的研究，较少涉及到交互效应影响下区间型多项目组合风险优化问题.2013年，杨瑞等[6]研究了三个或三个以上项目间存在交互效应的情况，提出了改进的多项目交互组合选择优化模型；杨颖等[7]采用关联性分配矩阵定量化描述了三个及以上项目共同作用时的相互依赖程度，综合考虑项目间的收益依赖、资源依赖和技术依赖等关联特征，构建研发项目组合选择问题的非线性规划模型.

而复杂网络研究的目的之一是为了了解网络结构与网络功能之间的相互关系与影响，文献[9]针对加权复杂网络的特点，在对节点重要度进行评估时考虑了边权对其的影响，提出了改进的加权网络的节点收缩方法；文献[10-11]利用节点接近度和节点在其邻域中的关键度对节点的重要度进行评估的方法，提出了利用节点重要度评价矩阵来确定关键节点，提高了节点重要度评估的效率和有效性；文献[12]利用节点的影响力来判断网络中的关键节点．由以上研究可知，关于交互效应下的多项目组合风险问题的研究与复杂网络具有相似性.2015年，管杜鹃等[13]基于复杂系统的视角，利用等级全息建模法(HHM)，从不同层级识别风险因素，建立交互效应下多项目组合风险网络；并依据复杂系统的脆性理论，得出了项目组合脆性风险的内因是由交互效应所构成的项目间的交互耦合结构引起的[14]；提出了基于贝叶斯网络的新的组合风险的度量方法[15].

鉴于此，本文运用复杂网络理论研究交互效应下区间型多项目组合风险优化问题，利用网络的统计特征分析项目的影响力及组合的稳定性，依据项目成功概率及对其他项目成功概率影响力的大小对项目组合进行优化，并得到组合网络中各项目的重要性，构建区间型多项目组合风险优化模型，得到了项目组合的最优风险.

1基于复杂网络的多项目组合风险适应性分析

1.1项目组合网络分析

复杂网络，即具有高度复杂性的网络，其节点具有多样性、数目巨大等特点，且网络结构复杂.而交互效应下的区间型多项目组合风险中的项目具有多样性，且随着项目数的增加，项目间的相互影响越来越复杂.基于此，可尝试利用复杂网络理论对多项目组合风险进行分析与优化，而复杂网络中分为无向无权、无向加权、有向无权与有向加权四种网络，根据多项目组合风险的具体情况，对项目组合网络分析如下：

(1)在组合中，若项目间存在相互影响，则认为项目间存在一条连边；若项目间不存在相互影响，则项目间无边相连.其连边上的数值，即权值，表示项目间相互影响的大小；

(2)当项目间存在交互效应的影响时，其影响值为一非零数，即权值不为零，从而研究交互效应影响下的多项目组合风险需要用加权网络，故本章中对无权无向及有向无权网络不进行讨论；

(3)当项目间存在相互影响，且其影响值大小相同时，可采用加权无向网络对项目组合进行描述，其影响值的大小表示为项目间相应连边的权重值；

(4)若项目间存在相互影响，且其相互影响是不对称的，则利用加权有向网络对其进行描述.项目间存在的不对称的相互影响及影响力的大小，使用网络中的有向边及相应边上的权值表示.

1.2项目组合网络统计特征分析

假设复杂网络G(V,E)，有N=|V|个节点，M=|E|条边.复杂网络常用的统计特征有：度(degree)，介数(Betweenness Centrality)，聚类系数(Clustering Coefficient)，平均路径长度(Average Path Length)，中心性等.其在多项目组合网络中的含义如下：

(1)项目节点v的度值d：表示与项目v存在交互效应影响的项目个数，即项目v对整个组合网络的影响范围；

(2)项目节点v的介数b：表示项目v对于网络中项目对之间沿着最短路径传输信息的控制能力，即项目v的介数越大，其对信息传输的控制能力越大；

(3)项目节点v的聚类系数C：表示各项目之间关联影响的密集程度，表示项目间相互影响的广度；

(4)网络的平均路径长度L：表示项目间相互影响的深度，体现网络弹性的大小，对外界信息变动的适应能力；当L值较小时，则说明组合网络对外界信息的变动的适应能力较强，能够及时应对突发情况；

本文运用复杂网络原理对区间型多项目组合风险进行优化，利用网络的度、介数及聚类系数来对项目组合风险进行分析及优化.

2区间型多项目组合风险优化模型

构建基于交互效应的项目成功概率的影响网络D1=(V,E,W1)，其中，W1表示两项目间成功概率影响值.因项目在执行过程中的不确定性，其成功概率的影响大小往往在一个范围内波动，故其数值呈现出区间数的形式，其数值构成的矩阵记为A ，如下：

其中，aii(i=1,2,…,N)表示项目单独实施时的成功概率，为一确定数，其数值由管理者根据以往同类项目的实施情况进行评估；aij(i≠j)表示交互效应下项目i对项目j成功概率的影响量.

利用交互效应下项目间成功概率的影响大小对组合网络进行优化，而在项目组合中，项目vi的成功概率P(vi)由项目本身所具有的成功概率aii及其他项目对其产生的影响Apt(vi)构成；即在交互效应影响下，组合中项目成功概率越高，其面临的风险越小.而在交互效应影响下当项目vi成功概率P(vi)较小，且vi对其他项目成功概率的影响Con(vi)较小或造成负影响时，则将项目vi从组合网络中剔除，从而达到对组合风险的优化.在有向加权网络D1(V,E,W1)中，项目vi受到的成功概率的影响量记为：

(j=1,2,…,N;i≠j)

(1)

同理，可得项目vi对组合中其余项目成功概率的影响量如下：

(j=1,2,…,N;i≠j)

(2)

由此可知，在交互效应影响下，组合网络中项目vi的成功概率为：

p(vi)=aii+Apt(vi),i=1,2,…,N

(3)

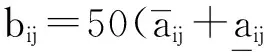
表1　项目组合优化

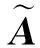
(4)

3风险分析

设原始项目组合网络的风险为R1，优化后的项目组合网络的风险为R2．分别计算网络原始组合网络D1与优化后的网络D2中各项目节点的聚类系数与介数.对单个项目在整个组合中的作用，及整个网络的风险进行分析，结果如下：

(1)当网络中项目vi的聚类系数Ci与介数bi均较大时，说明项目vi与其他项目的关系较紧密，对网络的影响范围较广，且处在关键通路的位置.一旦项目vi不能正常运行，其网络的整体风险会增大，从而当这种类型的项目进入组合时，需要管理者重点保护与扶持.

(2)当网络中项目vi的聚类系数Ci较大、介数bi较小时，说明项目vi与其他项目的关系较紧密，但没有处在关键通络的位置，因此管理者需保证项目vi能够正常运行，维持或者降低项目本身所具有的风险，并提供相应保护措施.

(3)当网络中项目vi的聚类系数Ci较小、介数bi较大时，说明项目vi与其他项目的关系一般，对组合风险产生的影响力较小，但其处在关键通路的位置上，部分信息必须通过项目vi才能传递到网络中的其他项目.因此管理者必须保证项目vi能够正常运行，以维持网络信息的传播.

(4)当网络中项目vi的聚类系数Ci、介数bi均较小时，说明项目vi与其他项目的关系一般，且不在关键通路的位置上，因此管理者可考虑不实施项目vi．

其算法流程图如图1所示.

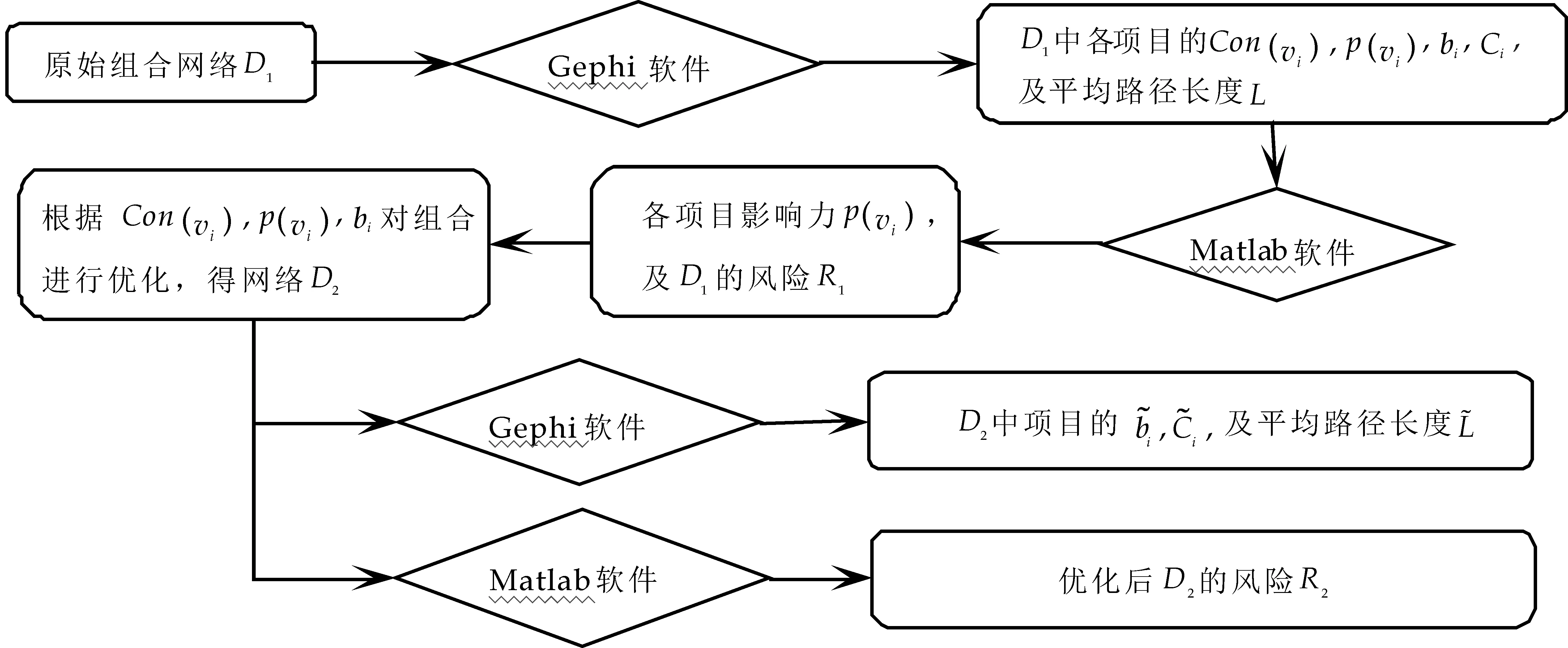
图1　算法流程图

4Matlab实现与算例分析

算法运行环境为：处理器Intel(R) Core(TM) i3-4030U CPU@1.90 GHz，内存4 G，硬盘465 G，操作系统为Windows 8，编程语言为Matlab R2012b．算法测试数据如下：假设有10个项目，构建交互效应下项目间成功概率的复杂度网络D1，各项目间成功概率的变化值记为矩阵A.

从而可得矩阵B为：

则项目间交互效应网络如图2所示.

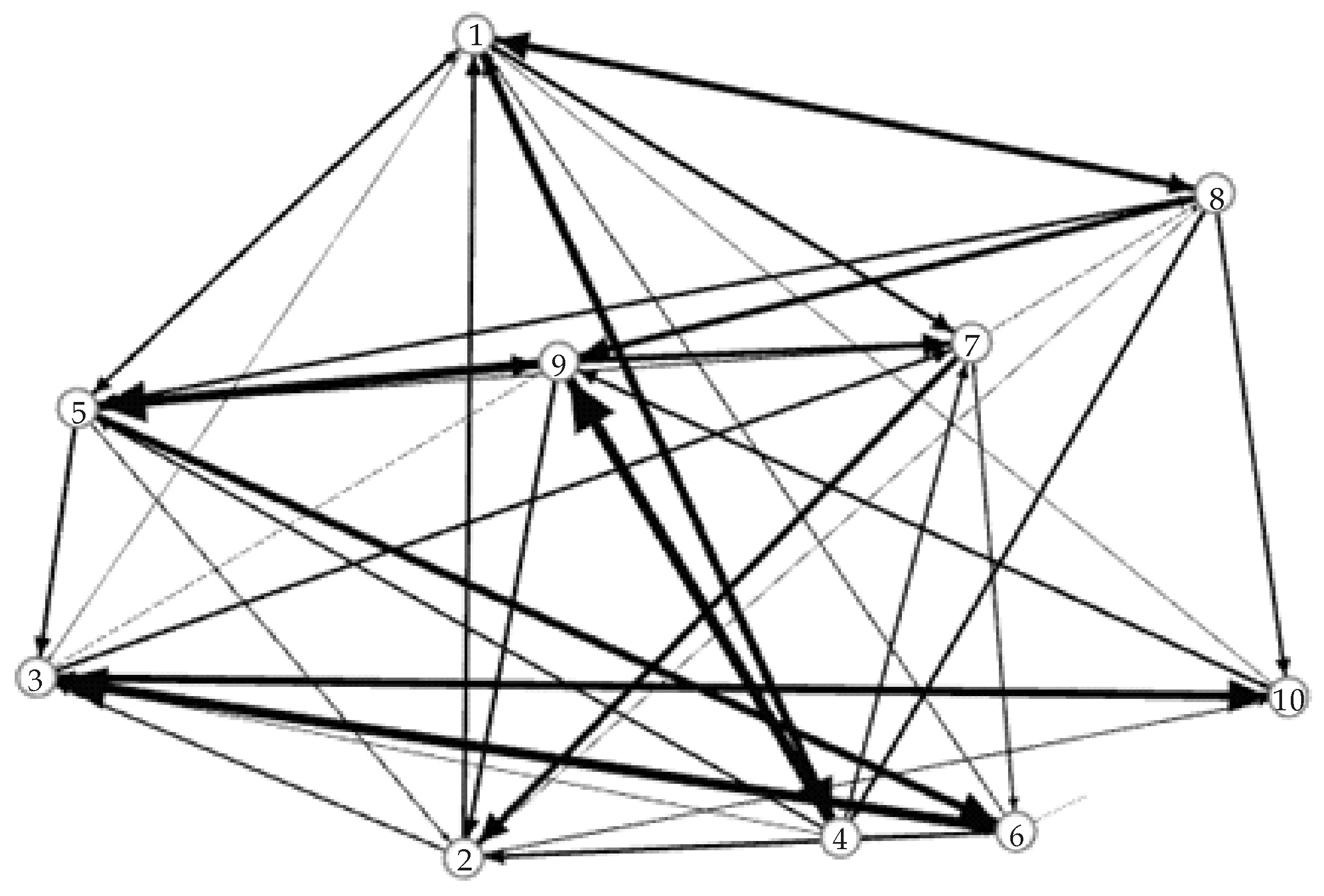
图2　交互效应下项目间成功概率影响网络

在图2中，项目间的连边越粗，则说明在交互效应影响下，相应项目间的影响越大；反之，则说明其影响越小.在网络D1中，若所有项目均实施，则将所需信息输入Matlab程序可得在交互效应下，各项目的成功概率P、组合风险值R1，并利用Gephi得到网络的平均路径长度L1、聚类系数C1和介数b1分别为：

P=([0.92,1.00],[0.90,0.97],[0.73,0.80],[0.93,0.99],[0.78,0.82],[0.85,0.99],[0.92,1.00],[0.59,065],[0.77,0.92],[0.95,0.98])

R1=[0.634 5,0.852 0];L1=1.444;

C1=(0.500,0.554,0.536,0.571,0.571,0.548,0.554,0.524,0.452,0.533);

b1=(5.750,3.533,5.083,2.833,3.783,3.083,4.533,3.950,5.333,2.117);

Con(v)=([0.28,0.4],-[0.04,0.05],[0.25,0.41],[0.01,0.07],[0.19,0.38],-[0.09,0.12],-[0.13,0.18]),[0.35,0.47],[0.10,024],[0.18,0.24])

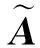
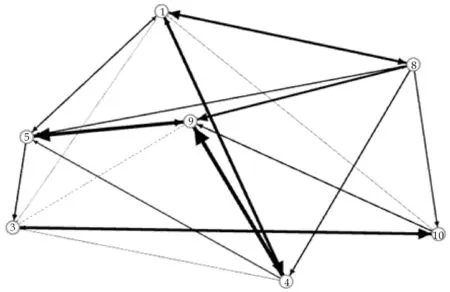
图3　优化后的交互效应下项目间成功概率影响网络

R2=[0.304 1,0.593 4];L2=1.452;

b2=(4.750,1.750,0.500,1.333,2.583,5.500,2.583);

C2=(0.40,0.55,0.60,0.55,0.55,0.40,050).

对组合网络D2进行风险分析可知如下结论：

(1)项目3、4、5的介数最小，但聚类系数最大，说明项目4对组合风险的影响较大，但不处在关键通路的位置，故需要管理者采取相应的措施进行保护与扶持；

(2)项目1和项目9的介数较大，但其聚类系数较低，处在关键通路的位置，故在执行过程中管理者需保证项目的正常运行；

(3)项目8、10的聚类系数和介数均较大，说明这些项目的组合风险的影响较大，且处在关键通路的位置，其实施情况对组合风险将产生较大影响，为控制组合风险，需要管理者重点保护与扶持；

(4)网络D2对外界信息变动的适应能力较优化前的组合网络D1无明显变化.

由以上分析可知，项目组合经过优化后，其优化后的风险较之前有较大降低；通过对项目节点的分析，得到对组合风险产生重要影响的项目，为管理者进行风险控制提供了有效的方法.

5结论

运用复杂网络理论研究了交互效应下区间型多项目组合风险优化问题，能够较直观的看到各项目间的相互影响及大小，利用复杂网络的统计特征分析各项目在组合网络中的重要性，并对组合网络进行优化，建立区间型多项目组合风险优化模型；利用计算机进行数值模拟，对比优化前后组合网络的风险值及对外界信息变动的适应能力，验证方法的有效性，提高运算效率，为管理者进行项目组合风险优化提供了一定的理论依据和方法.

参考文献

[1] Norman Baker,James Freeland.Recent advances in R&D benefit measurement and project selection methods[J].Management Science,1975,21(10):1 164-1 175．

[2] Robert L.Schmidt.A model for R&D project selection with combined benefit,outcome and resource interactions[J].IEEE Transaction Engineering Management,1993,40(4):403-410．

[3] 管杜鹃,郭鹏.交互效应及其影响度量下的项目组合关系分类[J].软科学,2014,28(10):125-129.

[4] 郭鹏,潘女兆,赵静.基于项目交互效应的高新技术项目组合风险研究[J].科学学与科学技术管理,2009,30(6):5-9.

[5] 赵静,郭鹏,贾颖颖.项目组合一致性风险测度及其选择决策研究[J].预测,2014,33(5):59-64.

[6] 杨瑞,王安民,张连营.改进的多项目交互组合选择优化模型[J].工程管理学报,2013,27(6):71-75.

[7] 杨颖,杨善林,马英,等.改进的基于多依赖性的R&D项目组合选择模型[J].系统工程学报,2011,26(6):834-841.

[8] Amir Hossein Ghapanchi,Madjid Tavana,Mohammad Hossein Khakbaz,et al.A methodology for selecting portfolios of projects with interactions and under uncertainty[J].International Journal of Project Management,2012(30):791-803.

[9] 朱涛,张水平,郭戎潇,等.改进的加权复杂网络节点重要度评估的收缩方法[J]. 系统工程与电子技术, 2009,31(8):1 902-1 905.

[10] 陈静,孙林夫.复杂网络中节点重要度评估[J].西南交通大学学报, 2009,44(3):426-429.

[11] 周漩,张凤鸣,李克武,等.利用重要度评价矩阵确定复杂网络关键节点[J].物理学报,2012,61(5):1-7.

[12] 刘欣,李鹏,刘璟,等.社交网络节点中心性测度[J].计算机工程与应用,2014,50(5):116-120.

[13] 管杜鹃,郭鹏.复杂系统视角下的项目组合风险构成及分析[J].管理现代化,2015,35(3):90-92.

[14] 管杜鹃,郭鹏.基于脆性联系熵的项目组合脆性风险分析[J].管理学报,2015,12(10):1 553-1 561.

[15] 管杜鹃,郭鹏.基于贝叶斯网络的项目组合风险度量[J].工业工程,2015,18(4):31-35.

【责任编辑：陈佳】

>The optimization research of multi-project portfolio risk based on the complex network under the interaction effect

WANG Chong-yang, ZHENG Wei-wei*, LIU Chen

(School of Science, Xi′an Polytechnic University, Xi′an 710048, China)

Abstract:In order to research the multi-project portfolio risk optimizing with the interval information and interaction effect.Used the statistical characteristics of complex network to analysis the importance and position of the project in the portfolio network,and used the probability of the project success and the amount of contribution to the other project success to optimize portfolio network, then constructed the interval multi-project portfolio risk optimization mode.According to the algorithm process, used the complex network software Gephi and Matlab programming design the process, improve the efficiency of the algorithm and validates the effectiveness of the method through the experiment.

Key words:project portfolio risk; interaction; complex network theory

*收稿日期:2016-04-30

基金项目：国家自然科学基金项目(71272049); 西安工程大学研究生创新基金项目(CX2015011)

作者简介:王重阳(1989-)，女，河南巩义人，在读硕士研究生，研究方向：最优化算法及其应用 通讯作者:郑唯唯(1962-)，女，福建莆田人，教授，博士，研究方向：生物数学、系统分析及优化，zww@nwpu.edu.cn

文章编号：1000-5811(2016)04-0187-06

中图分类号：O157.1;N945.15

文献标志码：A