基于扩孔理论的挤密砂桩桩身压缩模量理论计算方法

沈才华， 胡玉田， 孙雨婷， 许修亮， 徐　科

(1.河海大学 土木与交通学院， 江苏 南京　210098；　2.溧水区住房和城乡建设局， 江苏 南京　211200；　3.广东长大海外工程有限公司， 广东 广州　511431)



基于扩孔理论的挤密砂桩桩身压缩模量理论计算方法

沈才华1， 胡玉田1， 孙雨婷2， 许修亮3， 徐科3

(1.河海大学 土木与交通学院， 江苏 南京210098；2.溧水区住房和城乡建设局， 江苏 南京211200；3.广东长大海外工程有限公司， 广东 广州511431)

[摘要]采用了扩孔理论与沈珠江无粘性土体压缩模量的理论研究，推导了挤密砂桩不同反插比情况下桩体压缩模量的理论计算公式。同时结合具体的越南河内-海防高速公路工程项目，对不同土层、不同深度采用不同设计反插比，挤密砂桩桩体的压缩模量变化规律进行分析。得出主要结论为在反插比固定下，桩身压缩模量随c、φ值得变化大致呈线性变化。所研究的内容为开展挤密砂桩复合地基的设计起到非常重要的作用，可以为以后的设计与施工提供参考。

[关键词]压缩模量； 扩孔原理； 反插比； 挤密砂桩

1概述

近年来随着经济建设的需要，挤密砂桩地基处理技术不断被利用到软土地基处理工程中。近阶段由于机械设备的不断更新，使得挤密砂桩的反插扩容技术得到大幅度的运用。目前针对挤密砂桩作用下的复合地基的整体压缩模量及固结沉降沉降计算，国内外学者进行了大量研究。其中盛崇文、张定[1]等学者基于弹性理论对挤密砂桩复合地基进行研究，得出了复合地基沉降的简化计算方法；Priebe[2](1976)根据弹性半空间理论推导出复合地基在垂直荷载作用下的沉降量计算公式；Balaam[3]利用有限单元法来计算碎石桩作用下的复合地基沉降量以及沉降的速率；Omine[4]基于复合地基双重介质模型，利用桩土复合地基面积置换率得到桩土复合地基的复合模量；王凤池[5]考虑了桩长及桩端土性质的有关影响，进一步提出了桩土复合地基复合模量的修正方法。对于砂桩压缩的压缩模量，可按地基处理规范[6]根据桩侧土压缩模量、置换率和桩土应力比的经验值进行推算；石少敏[7]利用振冲器动力性能指标与砂桩桩体强度的关系，根据压缩模量概念，结合振冲桩制桩工艺，建立桩体压缩模量求解关系式。

挤密砂桩运用反插技术后，由于反插挤密作用，桩身压缩模量得到提高，使得挤密砂桩的复合地基的桩土应力比得到提高，但目前设计时还没有较好的理论公式来预测不同反插比条件下桩身压缩模量，这给采用复合模量法设计计算沉降带来了困难，因此本文基于扩孔理论推导了挤密砂桩桩身压缩模量理论计算方法。

2基于扩孔理论的挤密砂桩桩身压缩模量

计算方法

在砂桩反插处理后砂体会产生内压力，将会挤压桩周土体产生弹塑性区。这一特点，是与扩孔理论的研究类型是一致的。结合图1，在某一深度处，对灌入的砂体进行反插处理，根据扩孔原理得出在此反插情况下的桩周的径向位移。但在该研究过程中，首先需要做出如下假设[8]： ①土体是饱和均匀各向同性的理想弹塑性材料； ②小孔在无限大的土体中扩张； ③土体屈服服从莫尔-库伦屈服准则； ④孔扩张前，孔壁处土压力为静止土压力； ⑤砂桩桩体内砂为无粘结力，并不考虑其屈服变形。

2.1圆孔扩张理论介绍

基于理想弹塑性假定的Vesic扩孔理论是现在常用于分析各类沉桩挤土效应的有效方法。目前，圆孔扩张理论广泛应用于圆形隧道，井筒等的应力分析[9]。

本文基于圆孔扩张理论研究平面轴对称问题，简化计算土体单元如图1所示，扩孔过程中孔壁承受均匀分布的内压力pi，p0为外荷载。同时pc为临界扩张压力，砂桩套管半径为R0，塑性区半径为Rp，r为计算点处的半径，单元体径向应力σr，环向应力为σθ。在半径Rp以外的土体仍然保持着弹性平衡状态[10]。p0、pc的计算公式如下：

P0=K0·γ·Z

(1)

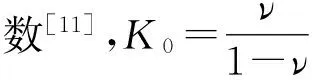
pc=ccosφ+p0(1+sinφ)

(2)

式中：c为凝聚力；φ为内摩擦角。

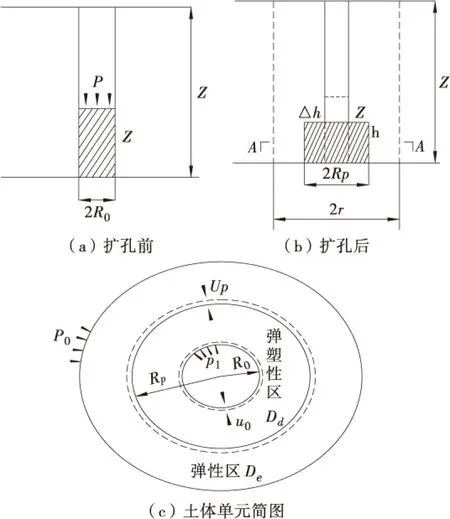
图1　土体计算单元示意图Figure 1　Schematic diagram of soil calculation unit

2.2基本方程

假设塑性区土体服从莫尔-库伦屈服准则，塑性区的径向应力为σr，环向应力为σθ，根据静力平衡条件Σr=0得出方程[12]：

(3)

几何方程满足：

(4)

弹性本构方程为：

(5)

(6)

塑性变形阶段采用Mohr-Coulomb准则进行理论计算[13]。莫尔-库伦屈服准则表示为：

(7)

以上皆规定压应力为正，拉应力为负。

由《土塑性力学》[12]以及沈珠江[13-15]所研究的内容中可以得出：

① 弹性区径向应力：

(8)

② 塑性区径向应力：

(9)

③ 在弹塑性状态下，塑性区域半径和位移场的解答为：

(10)

(11)

由上式可得出r=R0时，对应的桩周土位移。

2.3挤密砂桩反插比与砂桩压缩模量关系

根据沈珠江[16]所指出，对于无粘性土等向压缩试验的体积应变εν与固结应力p之间的关系，在双对数坐标系(lgεv-lgp)下近似为线性，即可用幂函数形式进行表示：

(12)

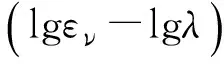
大量实验发现当初始孔隙比e0愈小，与其对应的t值也会愈小。而且发现截距t和初始孔隙比e0之间会呈现较好的线性关系，假定t和初始孔隙比e0之间可以用如下线性关系描述：

(13)

式中：k为(t-e0)直线的斜率；er为(t-e0)直线的水平轴截距，称作参考孔隙比。

由此可得出砂土等向压缩条件下的应力-应变的关系，可表示为：

(14)

式中：λ、k、er可查表1。

对于桩体一般选用圆形基底进行计算分析，结合工程实际中砂土类型为Sacramento River砂，其e0

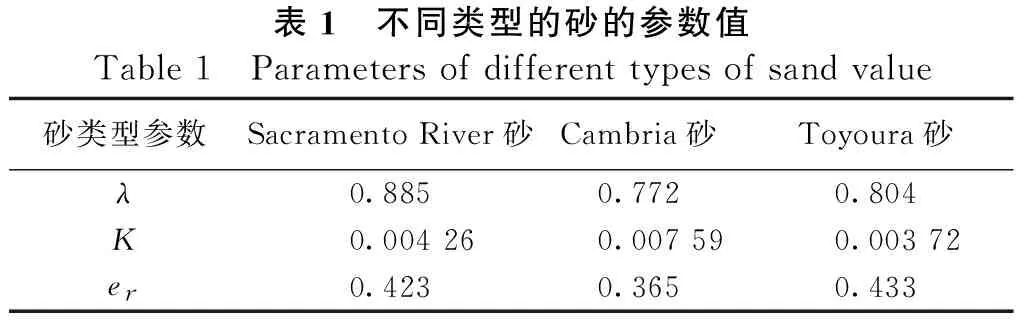
表1 不同类型的砂的参数值Table1 Parametersofdifferenttypesofsandvalue砂类型参数SacramentoRiver砂Cambria砂Toyoura砂λ0.8850.7720.804K0.004260.007590.00372er0.4230.3650.433

=0.912，pa=101.325 kPa。同时典型Sacramento River砂的压缩性测试得出其e-p曲线见图2[17]。

挤密后的砂体孔隙比可采用下式计算：

(15)

(16)

拟采用割线法求压缩系数av：

(17)

由此计算桩体的压缩模量Ep：

(18)

式(18)中pi为砂桩砂体所受的压力，根据简化计算模型(见图1)，把式(12)经过整理得出pi关于u0的变化关系公式，代入式(18)可得到挤密砂桩的理论压缩模量。

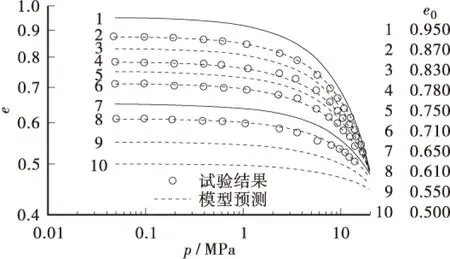
图2　Sacramento River砂e-p曲线Figure 2　Sacramento River sand’s e-p curve

2.4反插比与扩孔位移之间的关系

在深度Z下，假设在套筒半径为R0，灌入砂量高度为z后，进行反插处理。当反插深度为Δh时，此时可计算出反插比β，计算简图，见图3。

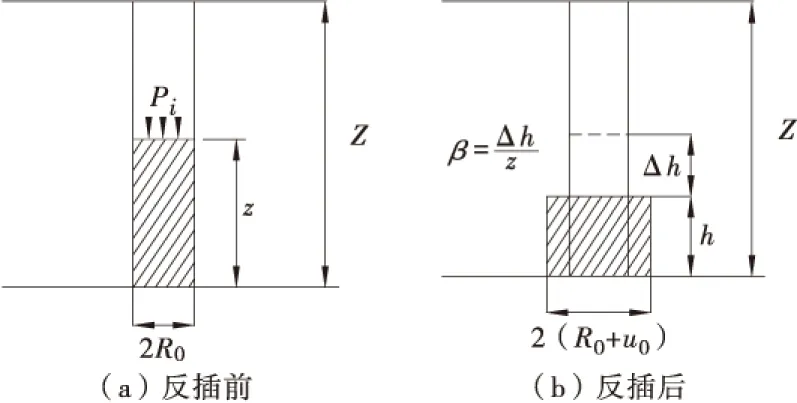
图3　反插过程计算简图Figure 3　The interpolation process diagram calculation

则有反插比与扩孔之间的关系推导如下：

(19)

式中：v为砂体反插前体积；v′为砂体反插后体积；h为反插结束后砂体的高度。

由式(19)可以得出：

(20)

据图3，得反插深度Δh为：

(21)

由反插比的定义，得反插比计算公式如下。

(22)

把式(11)与式(14)代入式(22)可以得出β的计算公式。

3反插比与桩体压缩模量应用研究

从而由扩孔理论与沈珠江无粘性土体压缩模量的研究。对内压力pi进行迭代直到设定的反插比大小，此时可以求解出在该反插比下所对应的桩体压缩模量。计算过程如下：

首先由式(14)代入不同的pi得出对应的体积应变：

(23)

将不同pi代入式(8)得出塑性区半径Rp：

(24)

求得塑性区半径后，再代入式(12)求解r=R0处的径向位移u0。

(25)

式中：μ为泊松比；E为土体压缩模量。

可利用εv与β的关系得出如下公式：

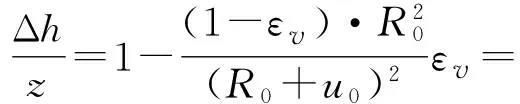
(26)

再利用式(27)等价关系，在求出扩容后砂体的孔隙比e1后，即可求解压缩系数av，公式如下：

(27)

Δe=εv(e0+1)

(28)

(29)

(30)

最终由式(18)求出扩容后桩体的压缩模量为：

(31)

可将公式(27)代入公式(31)得出反插比与桩体压缩模量的关系：

(32)

4实例应用研究

4.1工程介绍

本工程实例为越南河内-海防高速公路。地基处理设计主要选用砂井和挤密砂桩地基处理技术进行地基处理，其中所处位置为K0+668.98断面软土处理深度达30 m。其地基土层计算参数表见表2，其中v=0.3，根据土体参数计算出土体压缩模量Es=3.246 MPa。砂桩为矩形布置，按设计要求砂桩套管直径选为0.5 m，其间距1.5 m。

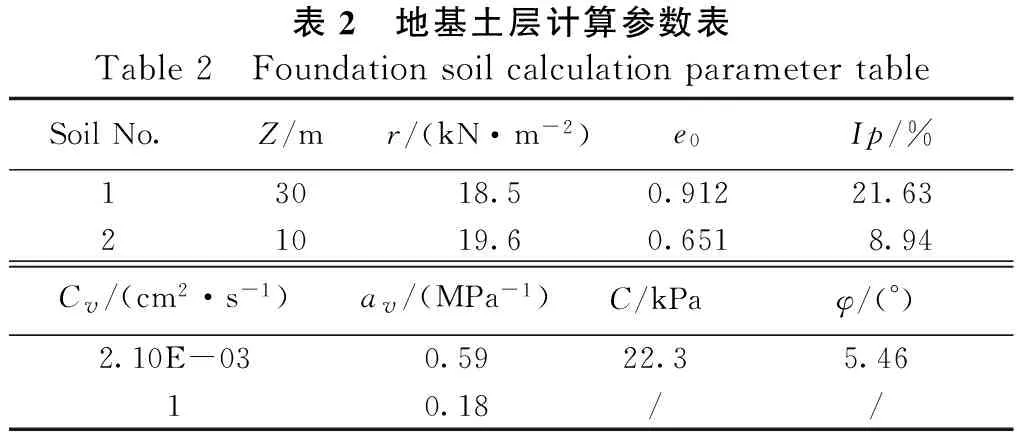
表2 地基土层计算参数表Table2 FoundationsoilcalculationparametertableSoilNo.Z/mr/(kN·m-2)e0Ip/%13018.50.91221.6321019.60.6518.94Cv/(cm2·s-1)av/(MPa-1)C/kPaφ/(°)2.10E-030.5922.35.4610.18//

4.2反插比规律性研究

砂桩处理深度为30 m，每10 m分一段，取5 m，15 m，25 m为每段平均值进行研究。

① 不同深度反插比与压缩模量关系变化。

反插比为不定时，取c为22.3 kPa，φ为5.46°研究。得出在不同深度反插比与压缩模量变化关系见图4。

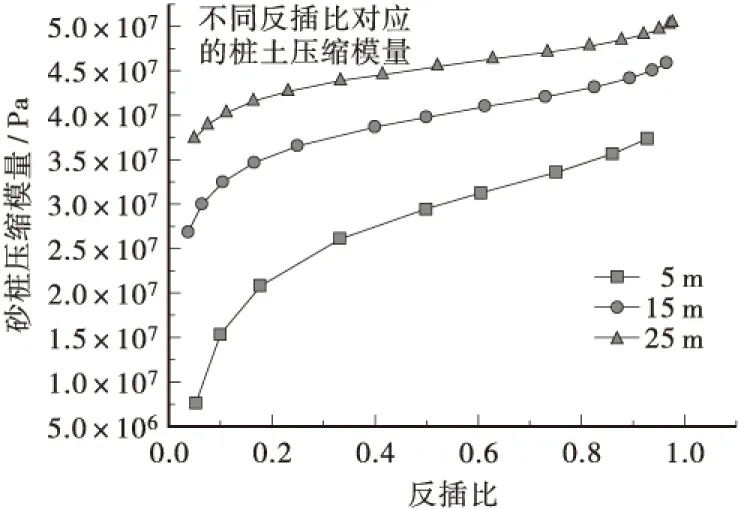
图4　在不同深度时不同反插比与桩体压缩模量曲线关系图Figure 4　In different depth when reverse anti interpolation ratio and modulus of pile compression curve diagram

② 假设反插比固定，得出砂桩压缩模量在不同c值情况下的关系曲线。

假设反插比为0.33、0.4、0.5时，c值选取值为22.3，25，30，…，50 kPa进行研究，得出变化关系曲线图，见图5。

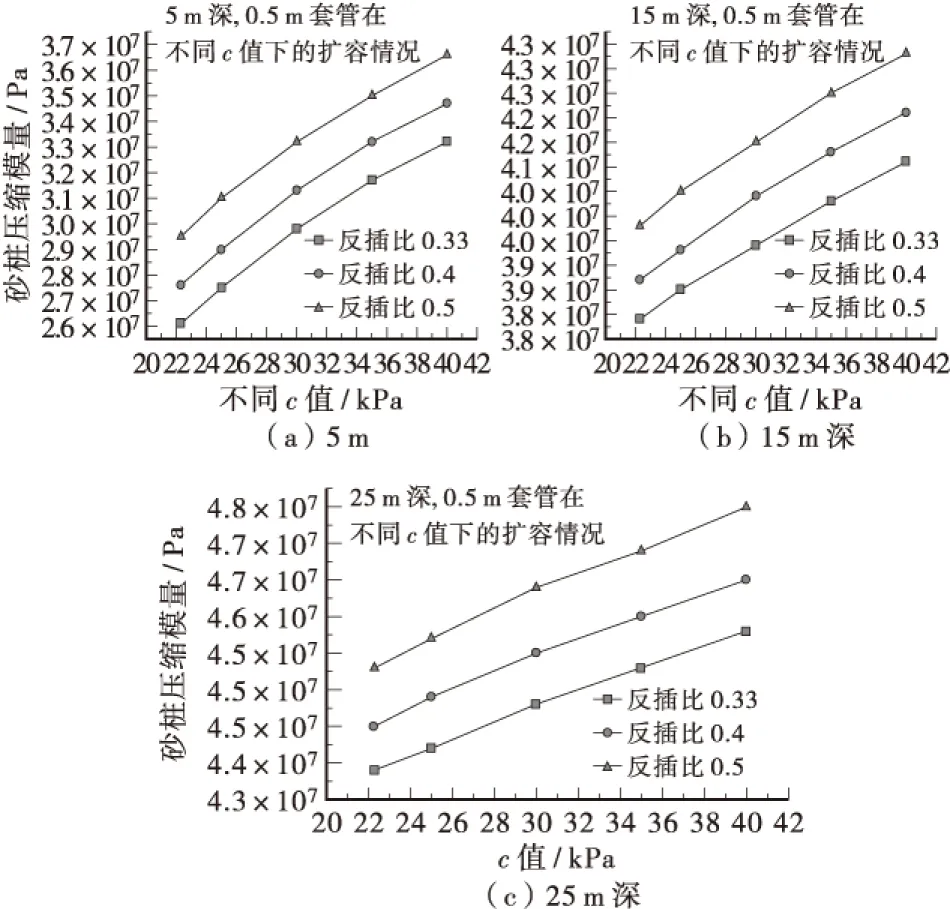
图5　不同c值条件下不同反插比与桩体压缩强度关系图Fig　　　ure 5　c value under the condition of different reverse anti interpolation ratio and strength of pile compression diagram

5小结

本文由扩孔理论与沈珠江无粘性土体压缩模量理论所推导出的计算公式，结合越南河内-海防高速路基处理的实际工程，引入挤密砂桩复合地基的反插扩孔理论研究。为验证扩孔理论公式推导的正确性，以及更好的研究扩容过程，在土体的具体c，φ值情况下得出了图4。在该图中可以明显的看出在不同深度处不同反插比与桩体压缩模量关系曲线的走势是大致相同的。在曲线开始段内，桩体压缩模量增长速度明显随反插比的增大而较快幅度的减少；在中间段处，增长幅度平缓；而在末尾段处，桩体压缩模量增长速度明显加快。

同时为了更好的指导挤密砂桩复合地基运用反插技术处理的设计，也假设反插比固定，得出砂桩压缩模量在不同c值情况下的关系曲线。由图5可以发现其对应的曲线大致呈现线性分布。同时当在研究不同φ值时，发现两幅图的曲线在不同深度，不同反压比的情况下，砂桩压缩模量的增幅大致都是相同的。从上面绘制的几幅曲线图可以发现，其与工程实际具有较好的吻合性。

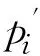
[参考文献]

[1]张定.碎石桩复合地基的作用机理分析及沉降计算[J].岩土力学，1999，20(2)：81 -86.

[2]Priebe H.J."Abschatzung des Setzungsverhaltens eines durch Stopfverdichtung verbesserten Baugrundes".Die Bautechnik，1976，5：160-162.

[3]Balaam N P，Brown P T.Settlement analysis of soft clay reinforced with granular piles[J].1977.

[4]Omine K， Ohno S. Deformation analysis of composite ground by homogenization method[C]//Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Enginee-ring.Rotterdam：Balkema A A，1997：719-722.)

[5]王凤池，朱浮声，王晓初.复合地基复合模量的理论修正[J].东北大学学报，2003，24(5)：491-494

[6]JGJ79-2002，建筑地基处理技术规范[S].

[7]石少敏.动力法计算振冲碎石桩桩体压缩模量[J].吉林大学学报：地球科学版，2011，41(1)：172-176.

[8]邓迎芳，莫海鸿，刘叔灼，等.应用圆孔扩张理论对静压桩挤土效应分析[J].广州建筑，2012(1)：23-26.

[9]徐书平，刘祖德，凡红.扰动对饱和软粘土园柱形孔扩张问题的影响[J].重庆建筑大学学报，2006(4)：63-67.

[10]章定文，刘松玉，顾沉颖.各向异性初始应力状态下圆柱孔扩张理论弹塑性分析[J].岩土力学，2009，30(6)：1631-163.

[11]龚晓南.高等土力学 [M].杭州：浙江大学出版社 ，1996.

[12]龚晓南.土塑性力学[M].杭州：浙江大学出版社，1990.

[13]蒋明镜，孙渝刚.考虑砂土颗粒破碎的圆孔扩张半解析分析[J].岩土工程学报，2009(11)：1645-1651.

[14]蒋明镜，沈珠江.考虑材料应变软化的柱形孔扩张问题[J].岩土工程学报，1995(4)：10-19.

[15]蒋明镜，沈珠江.岩土类软化材料的柱形孔扩张统一解问题[J].岩土力学，1996(1)：1-8.

[16]沈珠江.土的三重屈服面应力应变模式[J].固体力学学报，1984(2)：163-174.

[17]赵颜辉，朱俊高，张宗亮，等.无黏性土压缩曲线的一种数学模式[J].岩土力学，2011(10)：3033-3037.

The Sand Compaction Piles Based on the Theory of the Expanding Method to Calculate the Compression Modulus of the Sand Pile

SHEN Caihua1， HU Yutian1， SUN Yuting2， XU Xiuliang3， XU Ke3

(1.College of Civil and Transportation Engineering， Hohai University， Nanjing， Jiangsu 210098， China；2.Lishui District Housing and Urban Construction Bureau， Nanjing， Jiangsu 210098， China；3.Guangdong Changda Overseas Engineering Co.， Ltd， Guangzhou， Guangdong 511431， China)

[Abstract]This article makes a research by mainly adopting the reaming theory and the zhu-jiang shen cohesionless soil compression modulus theory，which deduces the theorical calculation formula of pile body compression modulus under the condition of different anti interpolation ratio of the sand compaction piles.At the same time，combined with specific Hanoi-haiphong highway project，we will use the different design anti interpolation ratio on basis of the depth and soil layer.According to the analysis on the change rule of sand compaction pile body compression modulus.We can get the main conclusion that pile body compression modulus will have the rough linear variation as the value c；changes based on the anti interpolation fixes.The contents of this paper are very important to start designing sand compaction pile composite foundation，which can provide reference for the future design and construction.

[Key words]composite foundation； reaming theory； anti interpolation ratio； sand compaction pile.

[收稿日期]2015-01-16

[基金项目]广东省交通厅科技项目(201302023)；江苏省普通高校研究生科研创新计划项目(SJLX_0210)；中央高校业务费项目编号(2014B27014)

[作者简介]沈才华(1976-)，男，江苏宜兴人，讲师，博士，从事岩土工程及地下工程方面的研究工作。

[中图分类号]U 443.15

[文献标识码]A

[文章编号]1674-0610(2016)03-0100-06