基于三次B样条多项式逼近的钢筋混凝土结构表面裂缝宽度概率评估方法
徐卫敏,雷 霆
(1.浙江建设职业技术学院,浙江 杭州 311231;2.上海容承企业管理有限公司,上海 210052)
基于三次B样条多项式逼近的钢筋混凝土结构表面裂缝宽度概率评估方法
徐卫敏1,雷霆2
(1.浙江建设职业技术学院,浙江 杭州 311231;2.上海容承企业管理有限公司,上海 210052)
确定混凝土表面裂缝宽度及其影响因素对海洋环境中的钢筋混凝土结构耐久性评估和设计非常关键,可作为沿海钢筋混凝土结构使用寿命的测度。在此提出了混凝土结构表面裂缝宽度评估的概率方法。将混凝土结构表面裂缝宽度达到容许值的时间定义为失效时间,基于三次B样条多项式逼近方法获得了与各随机变量相对应的失效时间的均值和变异系数。结果表明,当钢筋直径和锈蚀电流密度均服从正态分布时,失效时间分别服从正态分布和对数正态分布;保护层厚度、混凝土抗拉强度和弹性模量的变异性对失效时间几乎没有影响。最后,定量评价了钢筋直径和锈蚀电流密度对失效时间的影响。
钢筋混凝土结构;表面裂缝宽度;评估;概率方法
沿海地区的钢筋混凝土结构长期处于氯离子含量较高的环境中,氯离子侵蚀引起钢筋混凝土结构的严重锈蚀,主要表现为混凝土结构表面出现大量裂缝并伴随着部分保护层剥落,导致结构性能不断退化[1]。结构加固和维修不仅费用昂贵,而且给公众带来诸多不便[2]。在实际工程中,正常使用极限状态下以混凝土保护层的锈胀开裂作为钢筋混凝土构件寿命终结的标志,通常将混凝土结构表面裂缝宽度作为结构加固和维修的依据。因此,需对氯离子侵蚀导致结构开裂的过程进行研究,观测裂缝的发展并确定裂缝宽度,分析其主要影响因素,这对于结构最优化维修策略的制订起着重要的作用。
国内外学者针对氯离子侵蚀引发混凝土结构表面开裂方面展开了大量的研究,理论分析大多基于有限法确定锈胀力并预测开裂后的混凝土性能,Molina等人将混凝土模拟成线性材料,研究混凝土中裂缝的扩展[3]。郑建军等人考虑混凝土的软化特性,导出了混凝土保护层锈胀开裂的解析解[4]。Li等人进一步提出了混凝土结构表面裂缝宽度的计算模型[5]。王海龙等人基于钢筋均匀锈蚀时混凝土的开裂试验现象建立了混凝土保护层开裂的计算模型,考虑了混凝土和钢筋的实际变形情况以及混凝土界面中的原始裂纹与缺陷,裂纹在钢筋锈蚀膨胀作用下的起裂、扩展情况,利用断裂力学和弹性力学得到了混凝土保护层开裂时钢筋的膨胀力和均匀锈蚀率的理论预测模型[6]。实验研究中,为了在较短的时间内获得实验数据,大多采用各种方法加速钢筋锈蚀[7-8]。如Andrade等利用电流密度加速法测得混凝土表面裂缝宽度值随时间的发展,并确定钢筋截面的减少量与裂缝宽度间的关系[1]。以上这些研究均基于确定性方法,没有考虑混凝土材料性能和外界环境因素的变异性。程功等人利用Monte-Carlo方法提出了混凝土结构表面裂缝宽度评估的概率方法。计算表明,为了达到稳定的计算结果,需要进行大量次数的模拟[9]。本文在前人工作的基础上,根据各变量的统计特征,利用三次样条函数对裂缝宽度进行拟合,提出了混凝土结构表面裂缝宽度概率评估方法。
1 混凝土表面裂缝宽度计算
为了方便起见,在分析混凝土保护层受力特性时,通常将它简化成如图1所示由钢筋和混凝土保护层所组成的厚壁圆筒[4,10]。图1中,D表示钢筋直径,C表示混凝土保护层厚度,该圆筒内外半径分别为a=D/2和b=D/2+C。当混凝土中的钢筋锈蚀后,铁锈厚度ds(t)是时间、钢筋直径和锈蚀电流密度的函数,可通过实验和理论分析来确定[7]。根据程功等人的理论推导[9],混凝土结构表面裂缝宽度为
(1)
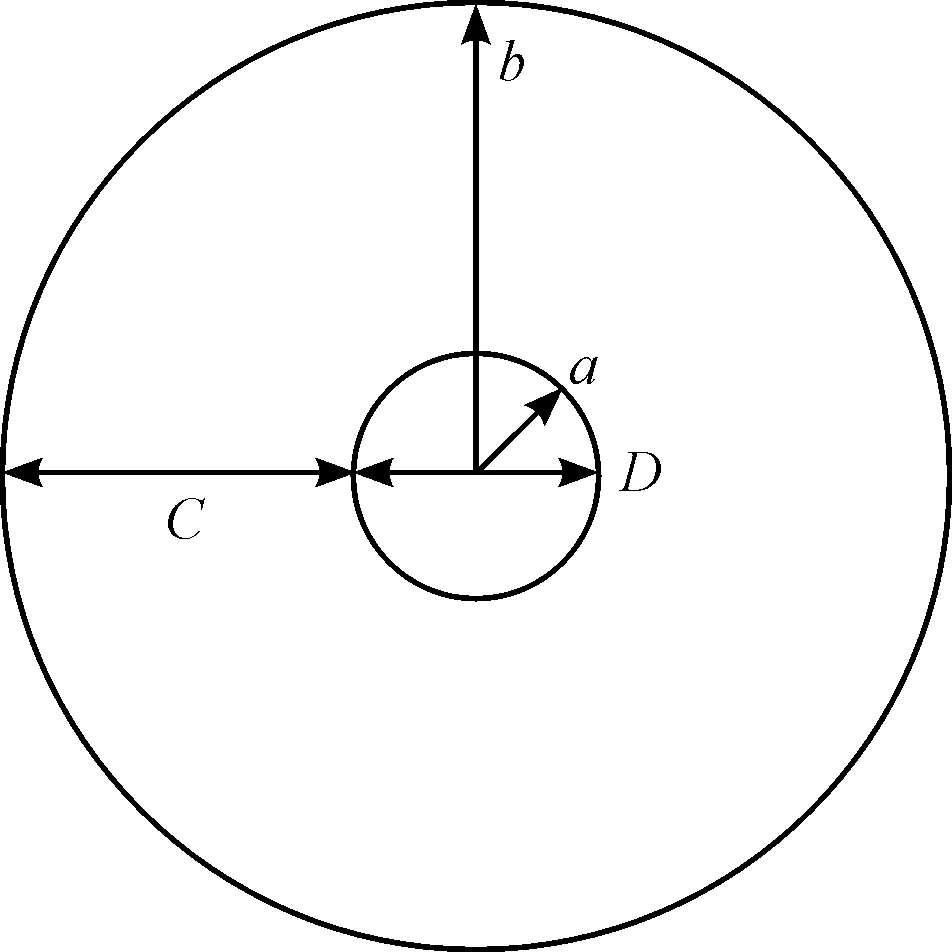
图1 混凝土保护层计算模型
2 三次B样条函数基本理论
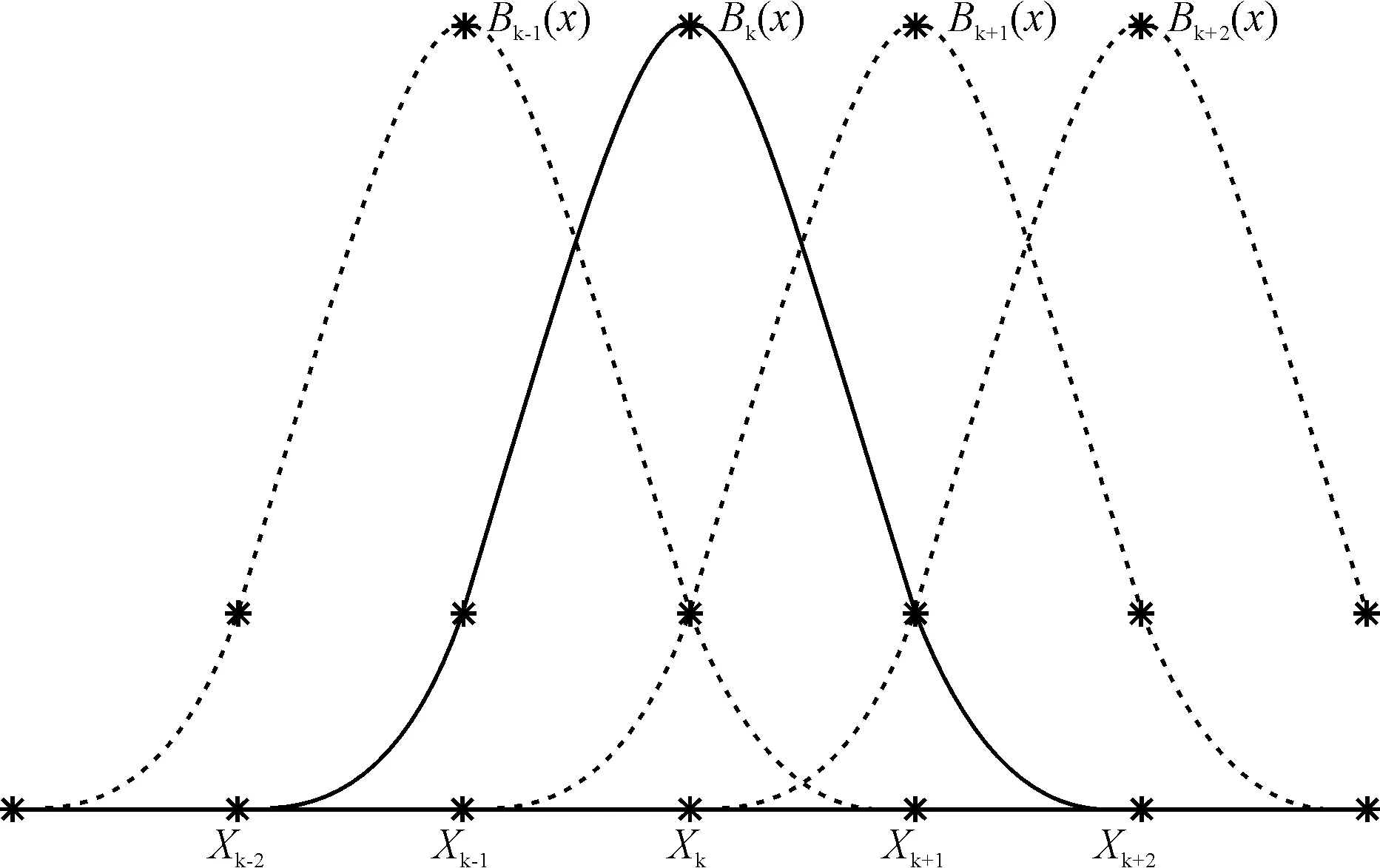
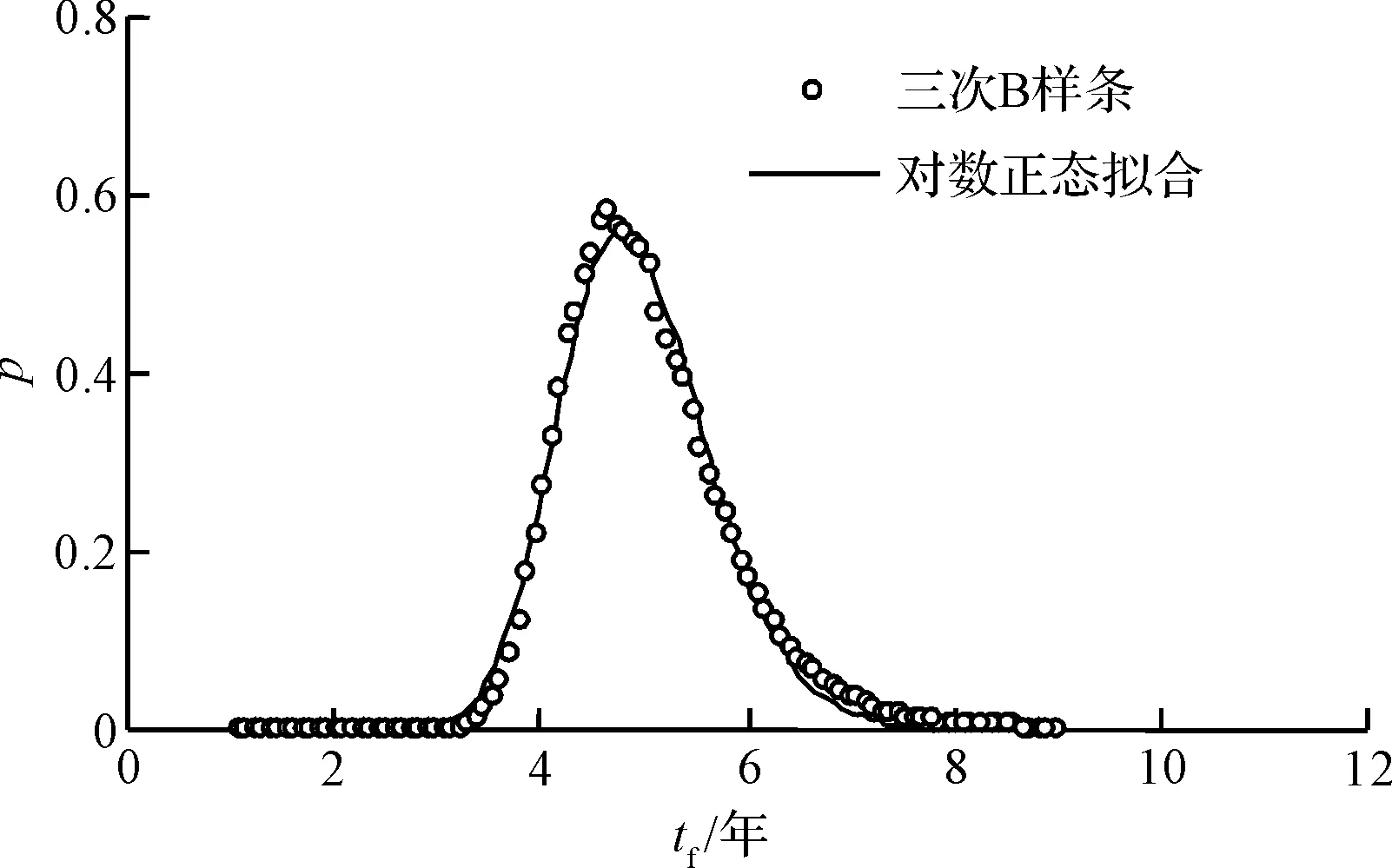
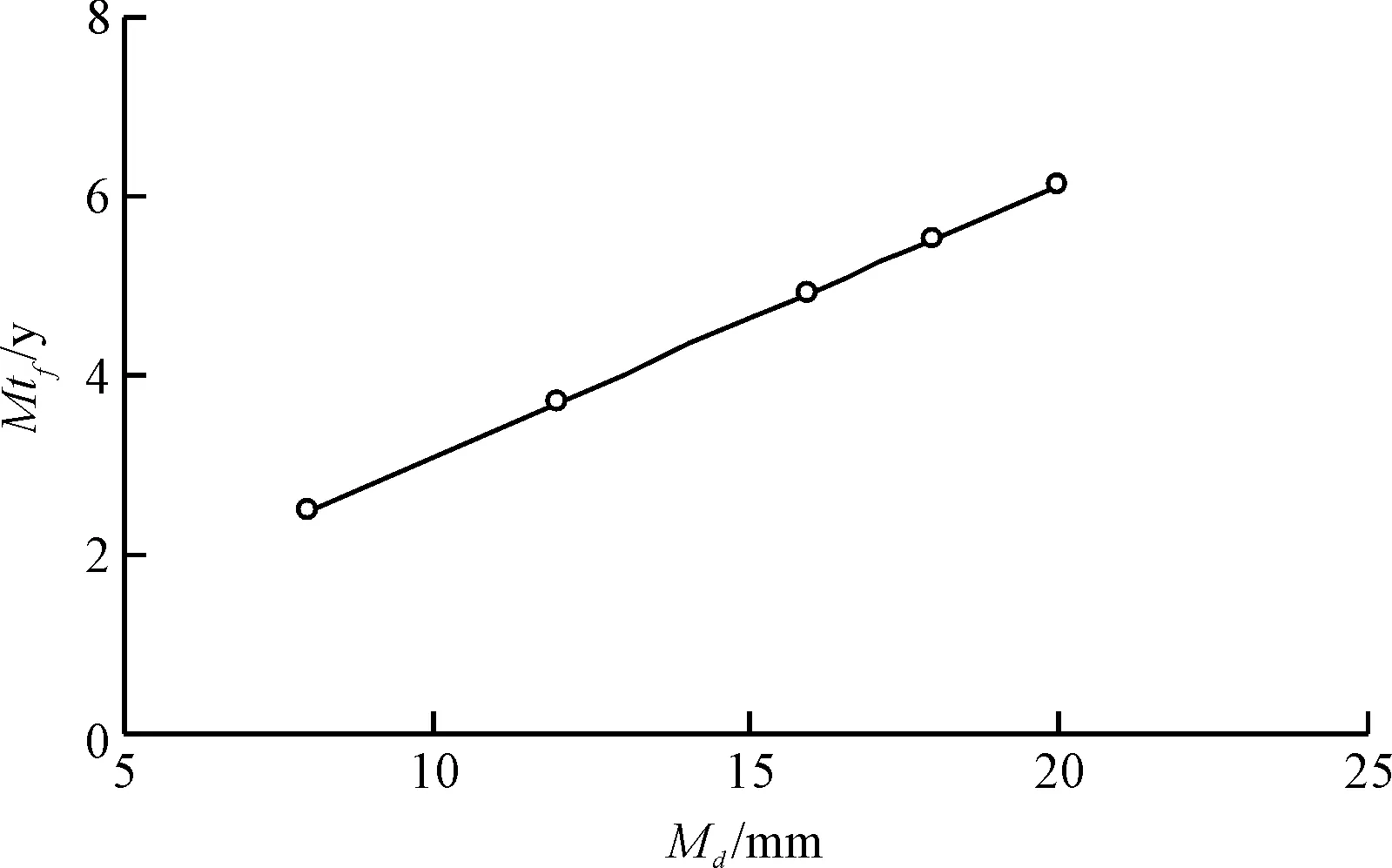
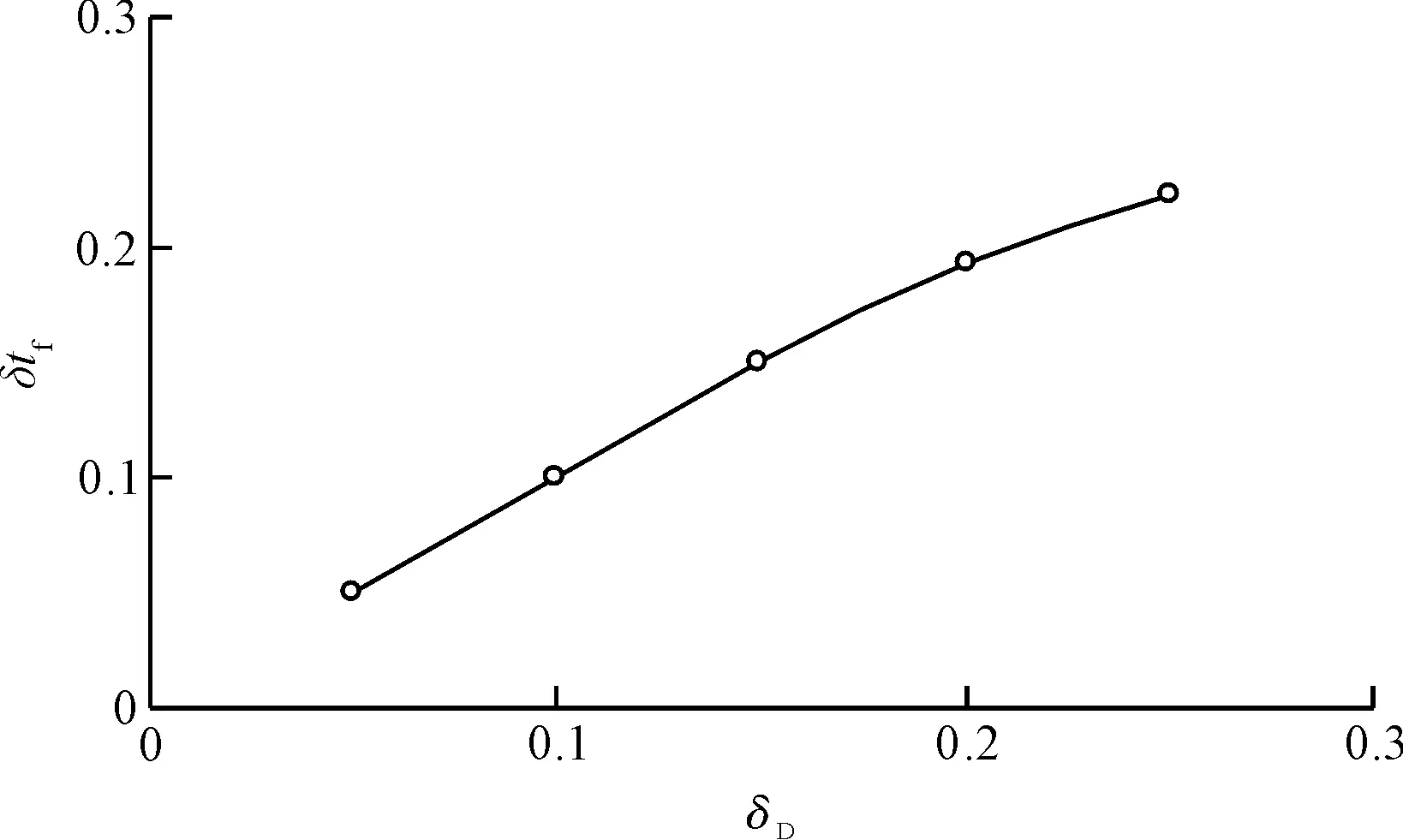
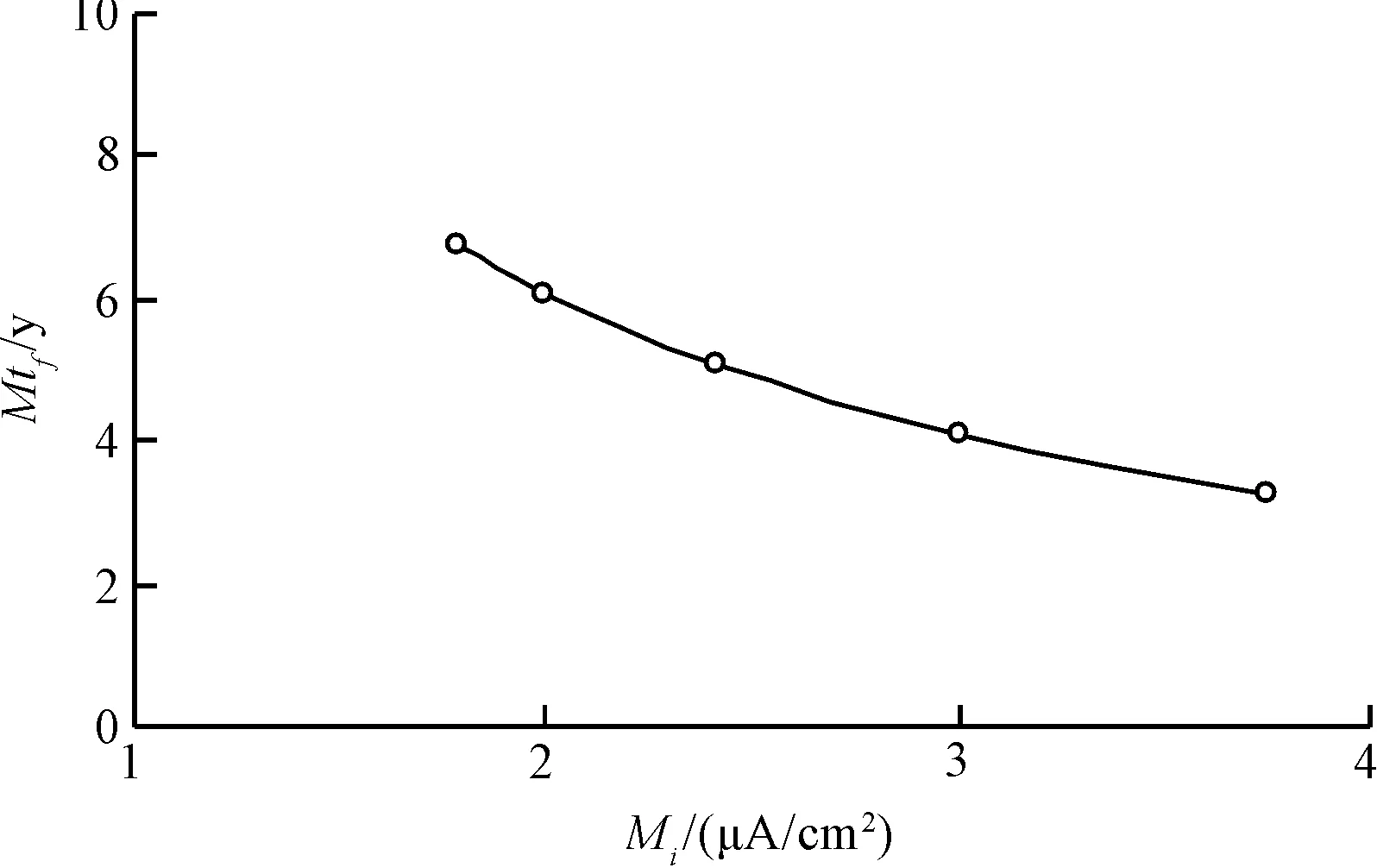
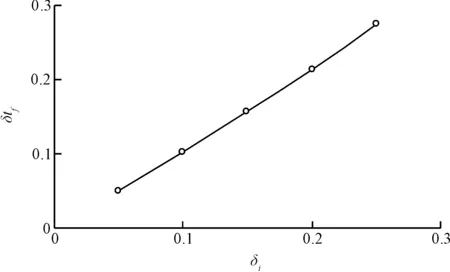
设[a,b]为给定三次样条函数逼近区间,且对区间[a,b]有剖分等距Δ:a=x0 (2) 节点xk上的B样条基函数Bk(x)可以由B0(x)向右移动k个节点确定,即Bk(x)=B0(x-kh+x0)。基函数Bk-1(x)、Bk(x)、Bk+1(x)以及Bk+2(x)如图2所示。值得指出是,这4个基函数在区间[xk,xk+1]上均不为零。 图2 三次B样条函数基函数 节点x0上的样条函数基函数B0(x)的二阶导数B″0(x)可以表示为: (3) 同样地,节点xk上的B样条基函数二阶导数B″k(x)可以由B″0(x)向右移动k个节点确定。 区间[x0,xn]上的函数三次样条函数S(x)可以表示为B样条基函数的线性组合,即 (4) 由于基函数B-1(x)在区间[x0,x1]、基函数Bn+1(x)在区间[xn-1,xn]不为零,因此式(4)求和考虑了B-1(x)与Bn+1(x)对样条函数S(x)的影响。 对于随机变量X概率密度函数fx(x),如果区间[a,b]取得足够大,可以假定区间[a,b]外的函数值为0。因此,根据连续性要求,区间[a,b]两端样条函数S(x)假设满足以下条件: (5) 根据B样条基函数特点,在节点x0处,S(x0)=C-1B-1(x0)+C0B0(x0)+C1B1(x0)。B-1(x0)、B1(x0)可由基函数B0(x)计算得到,即 (6) 这样就得到 0=S(x0)=C-1B-1(x0)+C0B0(x0)+ (7) 整理得, C-1+4C0+C1=0 (8) 同理有, Cn-1+4Cn+Cn+1=0 (9) 节点x0上样条函数的二阶导数S″(x0)=C-1B″-1(x0)+C0B″0(x0)+C1B″1(x0),B″-1(x0)、B″1(x0)可由基函数B″0(x)计算得到,即 (10) 这样就得到 0=S(x0)=C-1B-1(x0)+C0B0(x0)+ C1B1(x0)=h(c-1-2C0+C1) (11) 整理得, C-1-2C0+C1=0 (12) 同理有, Cn-1-2Cn+Cn+1=0 (13) 方程(8)、(9)和方程(12)、(13)共建立4个条件,剩余的n+3-(4)=n-1个条件可由随机变量X的前(n-1)阶矩确定。由于高阶矩在数值上存在不稳定性,本文在计算中采用前四阶矩。 随机变量X的k次矩μk定义为: (14) 利用样条函数S(x)近似逼近概率密度函数fx(x),则μk可以表达为 (15) 本文将表面裂缝宽度达到该容许值所对应的时间定义为失效时间tf。当混凝土保护层完全开裂后,表面裂缝成为氯离子扩散的新通道,加速钢筋锈蚀,导致表面裂缝宽度进一步增大。基于这一点,建筑规范中通常规定混凝土结构表面裂缝宽度的容许值wa作为结构加固和维修的依据,根据结构形式和环境条件,wa值一般在0.1~0.4mm之间,而美国ACI规范规定该值为0.3mm[1]。因此,本文在下面分析中,wa一律取为0.3mm。 由上述理论分析可知,影响tf的主要因素包括保护层厚度、钢筋直径、锈蚀电流密度、混凝土弹性模量和抗拉强度,在实际工程中他们往往具有一定的变异性。我们发现保护层厚度、混凝土抗拉强度和弹性模量变异性对tf几乎没有影响,在下面的分析中一律将它们看成是常数。因此本文仅对主要影响因素保护层厚度、钢筋直径和锈蚀电流密度进行分析,且均假设它们服从正态分布,其均值和变异系数见表1。在该表中,N()指变量服从正态分布,LN()指变量服从对数正态分布。 表1 各物理参数和tf的均值和变异系数 基于三次B样条函数逼近tf概率密度函数的计算步骤可归纳如下: (1)根据基本随机变量X的统计特征,对tf进行抽样; (2)根据抽样结果,计算tf统计数字特征,即各阶矩; 为了定量评价各参数对失效时间tf的影响,在下面的分析中,每次设其中一个参数服从正态分布,其余参数为定值,其数值等于它们各自的均值。 应用三次B样条拟合算法可获得由钢筋直径和锈蚀电流密度变异性引起的tf的概率密度函数P,其结果见图3~6,相应的均值和变异系数见表1。从这4张图可以看出,tf近似服从对数正态分布。为了进一步验证这一结论,利用上述采样所求得的均值和方差可获得相应的对数正态分布拟合,其结果见图3~6,从而可以看出,证实tf确实近似服从对数正态分布。 图3 由D的变异性引起的tf的概率密度函数 图4 由D的变异性引起的tf的累积分布函数 图5 由icorr变异性引起的tf的概率密度函数 图6 由icorr变异性引起的tf的累积分布函数 在分析钢筋直径D的变异性对tf的影响时,先设D的变异系数δD=0.15,可得到tf的均值Mtf与D的均值MD之间的关系,其结果见图7;再设MD=16 mm,同样可得到δtf与δD之间的关系,其结果见图8。从图7和图8可以看出,Mtf和δtf分别随着MD和δD的增大而几乎线性增大,一方面表明由于铁锈厚度与钢筋直径成反比,增大钢筋直径可有效地延长失效时间;另一方面也表明在设计中可以通过减小D的变异性来控制tf的变异性。进一步数值分析表明,当钢筋直径的均值MD从8 mm增大到20 mm时,Mtf增大149%。 在分析锈蚀电流密度的变异性对tf的影响时,先设锈蚀电流密度的变异系数δi=0.15,可得到Mtf和锈蚀电流密度的均值Mi之间的关系,其结果见图9;再设Mi=2.41 μA/cm2,同样可得到δtf与δi之间的关系,结果见图10。从图9、图10可以看出,由于铁锈厚度随锈蚀电流密度的增大而增大,Mtf随着Mi的增大而减小,而δtf则随着δi的增大而几乎线性增大。进一步的数值分析表明,当锈蚀电流密度均值从1.79 μA/cm2增大到3.75 μA/cm2时,Mtf减小52%。 图7 Mtf和MD的关系 图8 δtf和δD的关系 图9 Mtf和Mi的关系 图10 δtf和δi的关系 本文通过研究得到如下主要结论: 1)基于混凝土开裂后的控制方程,提出了混凝土结构表面裂缝宽度评估的概率方法。 2)数值模拟结果证实,当钢筋直径和锈蚀电流密度均服从正态分布时,失效时间分别服从正态分布和对数正态分布。 3)当钢筋直径的均值从8mm增大到20mm时,失效时间增大149%;当锈蚀电流密度的均值从1.79μA/cm2增大到3.75μA/cm2时,失效时间减小52%。 [1]ANDRADEC,ALONSOC,MOLINAFJ.Covercrackingasafunctionofbarcorrosion:part1-experimenttest[J].MaterialsandStructures,1993,26(8):453-464. [2]罗福午.建筑结构缺陷事故的分析及防治[M].北京:清华大学出版社,1996. [3]MOLINAFJ,ALONSOC,ANDRADEC.Covercrackingasafunctionofrebarcorrosion:part2-numericalmodel[J].MaterialsandStructures,1993,26(9):532-548. [4]郑建军,周欣竹,LiCQ.钢筋混凝土结构锈蚀损伤的解析解[J].水利学报,2004,35(12):62-68. [5]LICQ,ROBERTE,ZHENGJJ.Analyticalmodelforcorrosion-inducedcrackwidthinreinforcedconcretestructures[J].JournalofMaterialsinCivilEngineering,2007,19(7):591-600. [6]王海龙,金伟良,孙晓燕.基于断裂力学的钢筋混凝土保护层锈胀开裂模型[J].水利学报,2008,39(7):863-869. [7]LIUY,WEYERSRE.Modelingthetime-to-corrosioncrackinginchloridecontaminatedreinforcedconcretestructures[J].ACIMaterialsJournal,1998,95(6):675-681. [8]LICQ.Corrosioninitiationofreinforcingsteelinconcreteundernaturalsaltsprayandserviceloading-resultsandanalysis[J].ACIMaterialsJournal,2000,97(6):690-697. [9]程功,徐卫敏,郑建军.混凝土结构表面裂缝宽度评估的概率方法[J].浙江工业大学学报,2008,36(5):58-63. [10]BAžantZP.Physicalmodelforsteelcorrosioninconcreteseastructures-application[J].JournalofStructuralEngineering,1979,105(6):1155-1166. Appraisal Method of the Width Probability of Cracks on theSteel Reinforced Concrete Structure Surface Based on theApproximation of Triple B Spline Multinomial XU Weimin1, LEI Ting2 2016-04-13 徐卫敏(1982—),女,浙江台州人,工程师,从事建筑结构教学工作。 TU375 A 1008-3707(2016)06-0005-05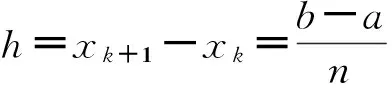
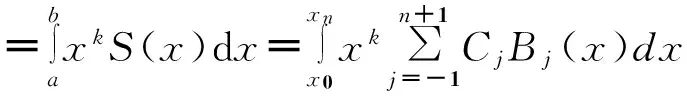
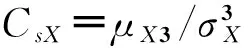
3 失效时间的统计特征和拟合
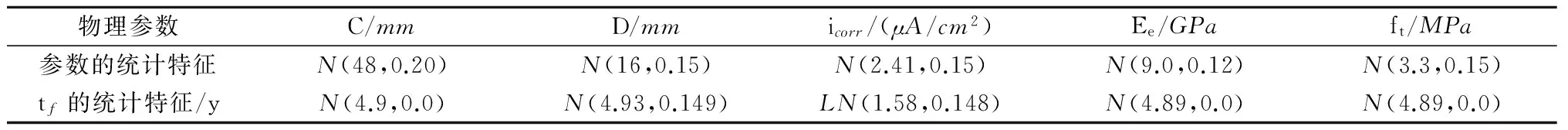
4 钢筋直径和锈蚀电流密度变异性的影响
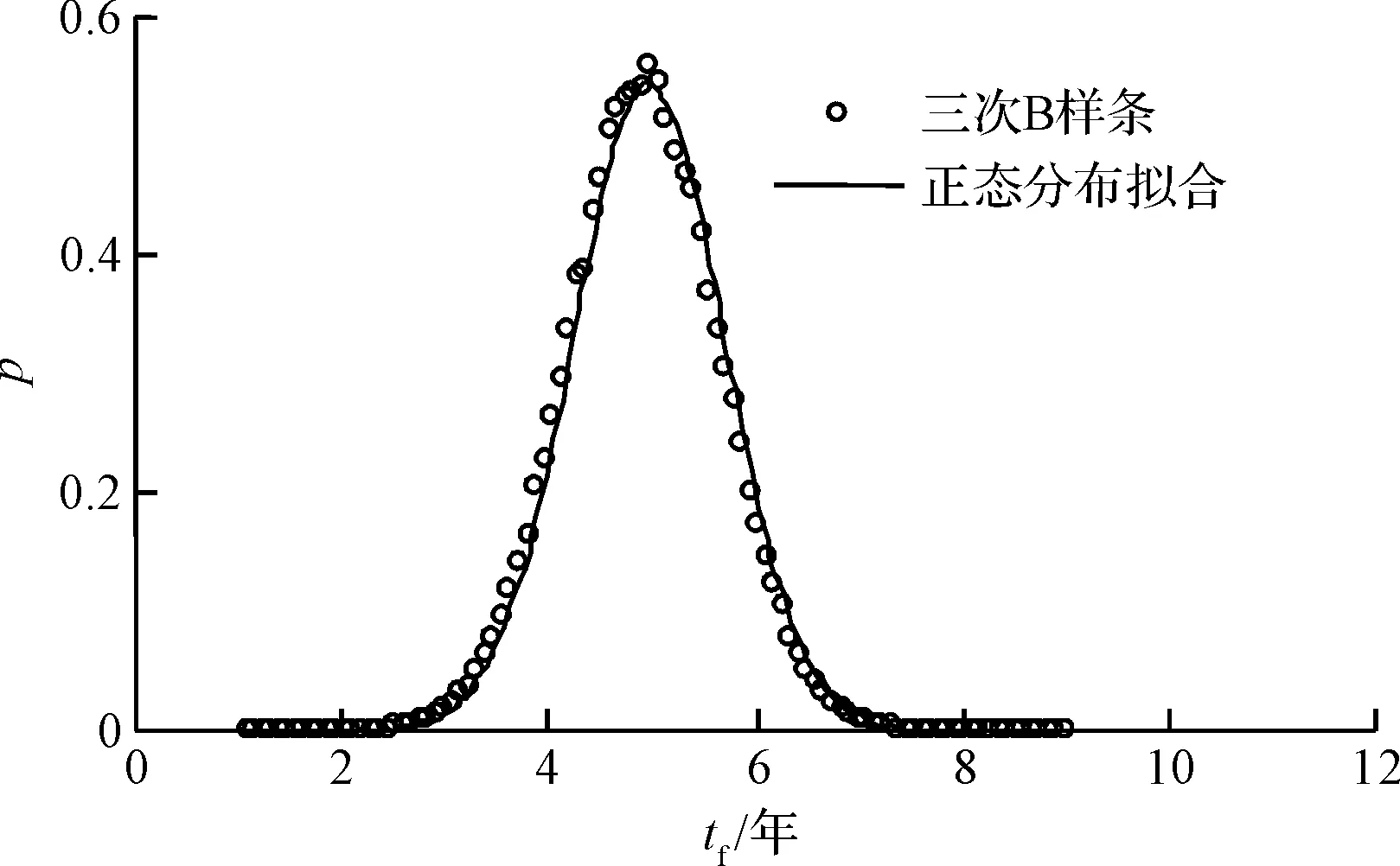
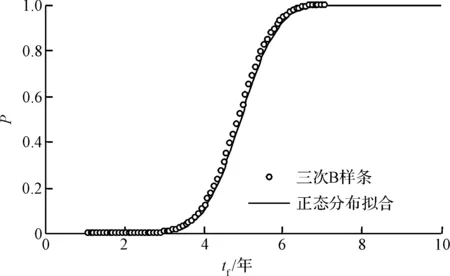

5 钢筋直径和锈蚀电流密度变异性对失效时间的影响
6 结 语

