沥青路面激光动态弯沉测试试验研究

武　韬， 付宏渊， 刘建华， 陈智敏， 董方卓

(1.长沙理工大学 土木与建筑学院， 湖南 长沙　410114；　2.长沙理工大学 交通运输工程学院， 湖南 长沙　410114；3.国家林业局 昆明勘察设计院， 云南 昆明　650216)



沥青路面激光动态弯沉测试试验研究

武韬1，3， 付宏渊1， 刘建华2， 陈智敏2， 董方卓2

(1.长沙理工大学 土木与建筑学院， 湖南 长沙410114；2.长沙理工大学 交通运输工程学院， 湖南 长沙410114；3.国家林业局 昆明勘察设计院， 云南 昆明650216)

摘要：分析了激光动态弯沉系统测试原理及其动态弯沉计算方法，针对已建成运营多年的高速公路由于施工、地质地形、交通流量、荷载等各种因素对路面弯沉的影响，路面的弯沉分布差异性变大，呈现偏正态分布的特点，基于激光动态弯沉测试技术开展了不同的测试速度与贝克曼梁的弯沉测试对比试验，试验结果表明：激光动态弯沉系统在相同的路面结构下采用40 km/h、60 km/h、80 km/h的速度测试与贝克曼梁仪所测试的数据均具有很好的相关性，相关系数分别为0.952、0.954、0.952，测试速度对于激光动态弯沉系统影响不大，其60 km/h测试速度与贝克曼梁仪的匹配性更好，由于采用激光动态弯沉测试方法得到的数据更加全面，其评价结果更加精确，具有一定的理论和工程应用价值。

关键词：道路工程； 沥青路面； 激光动态弯沉； 对比试验； 测试原理

我国柔性路面设计是以回弹模量作为设计参数，以弯沉作为力学控制指标。高速公路沥青路面在车载的作用下会发生变形，变形量称之为弯沉值，是路面结构强度的直接反映。在大量的交通轴载作用下，反复的较大路表弯沉变形会造成路面结构破坏，甚至可能造成某一结构层的断裂。弯沉值能表征路面结构承载能力，是路面检测中一项重要指标[1-3]。现行的高速公路养护中，在不影响车辆的正常行驶状况以及不损坏路面结构的前提下，为准确控制和评价高速公路的建设质量及使用服务水平，采用多种高新的测试技术是大势所趋。此外，对于已建成并运营若干年后的高速公路沥青路面，其路表弯沉值采集数据的统计分布特性往往不服从正态分布，呈现偏正态分布特性。对与此种分布方式，现有的处理方法有：去除变异值l±(2～3)S后，使用小波去噪，使其消噪后为正态分布，再直接计算代表值；去除变异值l±(2～3)S后，默认其服从正态分布，直接计算代表值。此两种方法都有不妥之处。其一，对于不属于正态分布的数据，运用l±(2～3)S法去除变异值是不可取的，由于检测仪器精确度上的差别，动态弯沉测试中处于l±(2～3)S以外的点很可能是路表弯沉的实际表达，所以不能随意去除；其二，小波去噪更使测试数据失真。

随着科学技术的发展，新技术的使用，检测手段不断智能化，无损化，高效率化，新的测试方法带来新的技术革命，主要是以计算机和各种机械电子设备代替人工测试，提高效率的同时也弥补了人为因素对检测结果的影响，减轻了劳动强度，提高了精确度，实现了智能测试[4-6]。新的高新技术的使用与传统的测试方法有不同之处，在检测和评价过程中必定产生差异。评定规范和评定准则存在滞后性，随着新技术的应用，需要找出原有评价方法的不足并加以完善，以满足新技术的需要。国内传统的强度评价只是采用了基于静态荷载作用下的评价指标，落锤式弯沉仪(FWD)在工程中的应用，动态弯沉参数的评价及弯沉盆的分析应得到更大的重视，对应的评价指标也需完善[7，8]。

弯沉测试中利用贝克曼梁仪采集得到的弯沉数据是卸载后的回弹弯沉。激光动态弯沉系统与落锤式弯沉仪(FWD)所采集的均为最大弯沉值，即标准荷载下弯沉测点在垂直方向所发生的总变形，与贝克曼梁所测弯沉有所区别。总的来说，这个总变形包含两部分，一部分是指弯沉测点在荷载作用下发生的塑性变形，即不可恢复的变形；另一部分为卸载后可恢复的部分，用回弹弯沉表征。而现阶段我国各类设计、检测养护规程中都是以回弹弯沉值当作评估标准。在这基础之上，应建立总弯沉与回弹弯沉的相关关系式，检验是否能达到规范要求。

为此，本文在相同路面条件下，采用激光动态弯沉系统与贝克曼梁检两种不同的测试方法开展路面弯沉测试对比试验，并根据两者所采集的数据从而建立总弯沉与回弹弯沉的回归方程，求出相关系数，对误差进行分析。

1激光动态弯沉测试技术

激光动态弯沉系统(滚轮式弯沉仪 RWD)是最理想的弯沉测试设备，它的弯沉测试原理是：系统在高速行驶过程中利用激光多普勒(laser-Doppler)技术，测试路面在车载作用下的垂直下沉的瞬时速度，通过分析系统中的几个激光多普勒的测试数据计算出最大弯沉及弯沉盆数据。

激光动态弯沉系统采用非接触检测方式工作，能以高达80 km/h的速度精确测试地面弯沉。其所记录的是真实受力状态，路面状况与实际行车荷载一致。该设备是高速公路弯沉检测设备的最佳选择，既可测量动态弯沉指标，又能以正常的行驶速度连续性检测，不影响现场交通组织。

目前，基于激光多普勒原理的高速激光自动弯沉系统的参数对比如表1所示。随着弯沉测试技术的快速发展，弯沉检测精度提高的同时，结构强度评价方法也应根据测试技术的变化而有所优化。

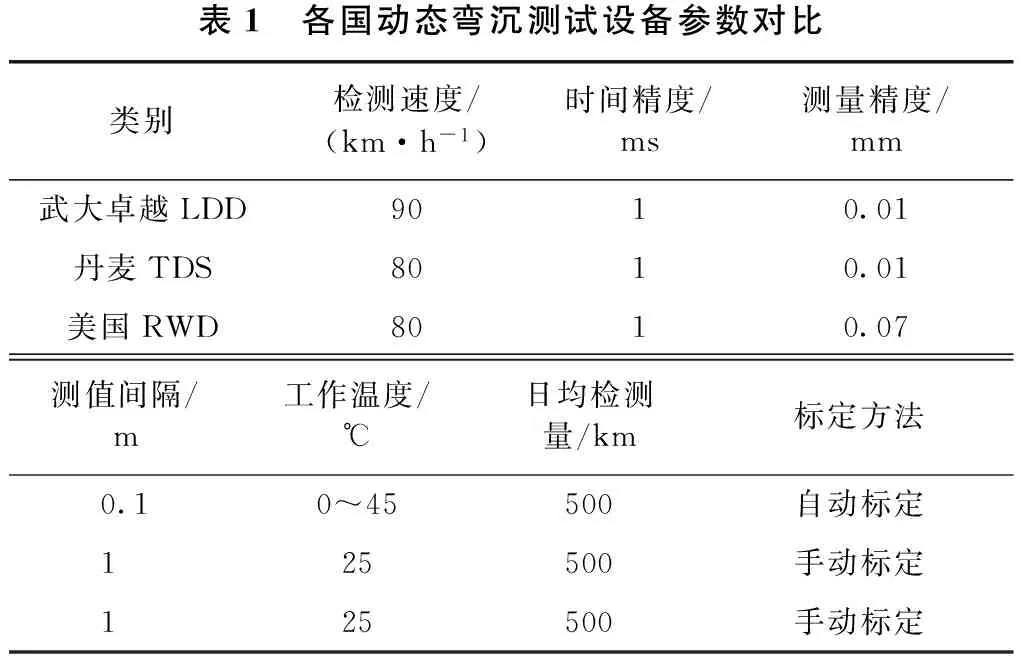
表1 各国动态弯沉测试设备参数对比类别检测速度/(km·h-1)时间精度/ms测量精度/mm武大卓越LDD9010.01丹麦TDS8010.01美国RWD8010.07测值间隔/m工作温度/℃日均检测量/km标定方法0.10～45500自动标定125500手动标定125500手动标定

激光动态弯沉车与原有检测设备优势对比，如表2所示。

表2 激光动态测试技术与传统测试技术对比比较项目贝克曼梁、FWD和自动弯沉仪激光动态弯沉测量系统备注快速性测试速度为1～3km/h测试速度15～90km/h,正常速度为60km/h是传统测试速度30倍以上连续性一般是每隔20～50m,测试一个测量点,属单点间隔采样连续测量,每隔0.1m输出一个测试值消除传统测试可能丢失间隔中的弯沉异常信息动态性运行速度较慢在车辆运行中动态测量更加符合公路使用现状安全性人身与仪器安全性差,有着被违章车辆擦碰或撞击的极大风险,尤其在运营中高速公路上以正常交通速度行驶,使用安全性好良好的安全性经济性需要全部和部分封闭运营道路;需要一个车队(2～3辆车);需要辅助设备正常行驶,不影响正常交通,除正常的保养和油料外,不需要其它费用测试经济性好人力消耗至少需要6个人员参与,野外作业,作业环境差,劳动强度大只需2人操作,数据报表自动完成,工作环境良好人力消耗量少效率单台设备每天的测试里程在10km左右500km效率是传统50倍及以上

由上表可以看出，各项指标都优于传统的测试方法。而弯沉测试效率提高的同时，合理的规划测试方案是进一步提高效率的方法。激光动态弯沉系统在弯沉检测中与落锤式弯沉仪(FWD)和贝克曼梁仪检测原理有所不同：

1) FWD是模拟行车荷载作用下的弯沉盆，从而得到最大弯沉值；贝克曼梁是利用静载作用产生的弯沉盆，所得到的回弹弯沉；而激光动态弯沉系统所测的是在真实移动轴载作用情况下实际产生的弯沉盆。

2) 两者的测量系统也不一样。测试路段表面达到最大弯沉时，速度降至零，计算弯沉盆分布各点速度变化获得弯沉最大值。相比较而言，激光动态弯沉车记录的为真实行车中的路面弯沉状态，测试结果为动态弯沉，而根据测量出路面的瞬时沉降速度、载车对路面的压力、路面的纵向起伏、车速、环境温度等信息，在这些信息的基础上根据路面弹性模型就能推导出路基的结构强度参数，换算成标准轮压下的弯沉值。

2激光动态弯沉测试原理

路面在重载车轮的碾压下会产生沉降，弯沉检测车通过速度传感器精确地测量出3个测量点的沉降速度。形变的速度越小路面强度越大，反之形变速度越大路面强度越小[9，10]。根据测量点相对于车轮中心的位置和它的沉降速度，利用弹性力学理论可以得到弯沉盆曲线的数学方程，再结合车轮的压力就能够算出标准弯沉值[11]。此处认为，车辆荷载作用在测试路面时，测试路表面的瞬时变化速度为零时，此时路表面处于最大弯沉阶段，根据测得各点速度变化，最终计算出最大弯沉值及路面弯沉盆分布(如图1所示)。

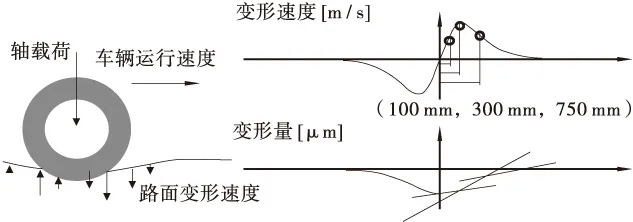
图1　最大弯沉值及弯沉盆分布

路面可以看成满足欧拉-伯努利方程的弹性模型(图2)。路面变形模型是指：路面单元如单个弹簧，无限细化组合成的弹性梁。此种变形运用弹

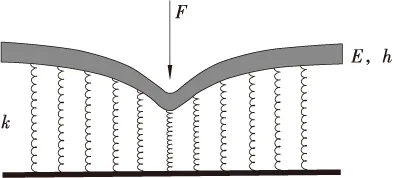
图2　沥青路面弹性模型

性力学原理可以用Euler-Bernoulli梁方程表达(如式(1))，F为作用中心的正压力，E是路面刚性，I是路面的转动惯量，k是弹性系数。

(1)

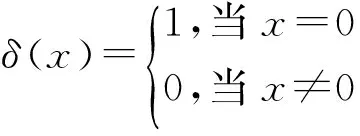
(2)

(3)

w′(x)=A(sin(Bx))e-Bx

(4)

式中：A，B为未知参量；w(x)为以x为变量的路面弯沉量函数；w′(x)为w(x)的导数，表示弯沉斜率；x为各个弯沉测量点到车轮中心着力点的距离值。

且：

w′(x)=R/Vhor

(5)

处理器根据里程编码器记录弯沉测量平台的运行速度及所运行的里程信息计算可以得到式(6)，其中R1、R2、R3、R4为第一、第二、第三、第四速度传感器所在位置的路面下沉速度：

(6)

式中：Vhor为测量车辆的水平速度；Ac为加速度计测量值；t为加速度计的测量时刻；VG为角速度传感器测量值。

而在实际应用过程中，由于车体自身震动，以及路面起伏等影响，造成速度传感器本身就有了速度或者角度的变化，因此速度传感器测得的速度，是速度激光器光线方向的合成速度。

由式(1)可知该微分方程的解是一个关于A和B的参数模型，其中X≥0，A>0，B>0。两参数欧拉-伯努利方程解为：

(7)

(8)

(9)

(10)

SCI300=w(0)-w(300)

(11)

式中：SCI300为结构曲率指数；w(0)为最大变形量。

根据式(6)和测得的数据可得到R1、R2、R3、R4处下沉的速度。车辆的水平速度Vhor可测量得到。将上述已知数带入式(5)可得：

w′(x1)=R1/Vhor，w′(x2)=R2/Vhor

w′(x3)=R3/Vhor，w′(x4)=R4/Vhor

(12)

将式(12)代入式(4)可得：

A(sin(Bx1))e-Bx1=R1/Vhor

A(sin(Bx2))e-Bx2=R2/Vhor

A(sin(Bx3))e-Bx3=R3/Vhor

A(sin(Bx4))e-Bx4=R4/Vhor

(13)

根据最小二乘拟合，求解A和B。将所求A和B根据不同的x值代入式(3)可知：

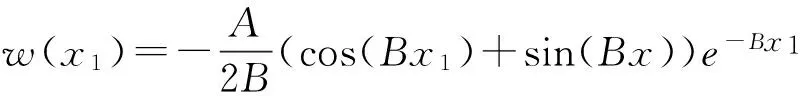
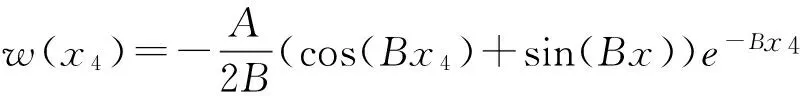
(14)

可求得w(x)，而所测得的弯沉由于受温度的影响较大，必须对其做温度修正。

W(x)=w(x)·Temp

(15)

温度校正系数如下：

Temp=0.001 24×T2-0.002 98T+1.096

(16)

将式(16)代入式(15)可得修正后的弯沉值：

W(x)=w(x)·Temp=

(17)

3激光动态弯沉测试对比试验研究

3.1试验设计

为全面对比激光动态弯沉系统测试效果，根据工程实际测试的需要，设计了在同一沥青路面结构下，采用激光动态弯沉测试系统采用不同的测试速度，与贝克曼梁进行比对试验，其试验路段路面结构见表3。

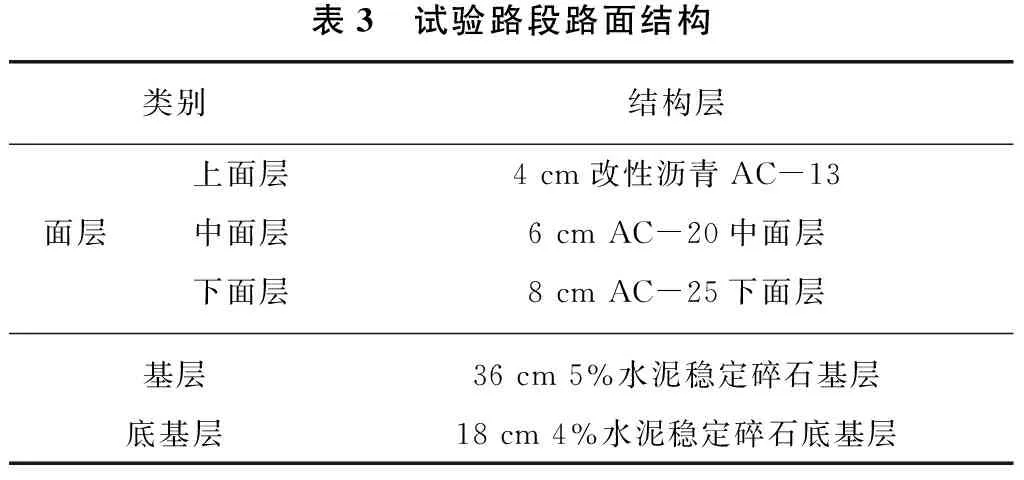
表3 试验路段路面结构类别结构层面层上面层4cm改性沥青AC-13中面层6cmAC-20中面层下面层8cmAC-25下面层基层36cm5%水泥稳定碎石基层底基层18cm4%水泥稳定碎石底基层

贝克曼梁作为弯沉的自动化测试设备的比对参照物，由于其受人为和周围环境的影响较大，在比对中更应该消除各方面不利的影响。故在比对前应注意因素[12，13]：

1) 测试前必须检查激光动态弯沉系统和检测车的各项基本指标，主要核查其荷载、轮压、及轮与路面的接触面积等，各项指标均需满足规程要求。

2) 由于温度对测试结果影响较大，弯沉对比试验应当选择在温度差异不大的环境中进行测试，对于激光动态弯沉测试得到的弯沉值是经过式(17)进行修正，将温度影响因素降低到最小。

3) 所选弯沉试验路段应尽量顺直，避开超高以及坡度变化较大的地方，减小横坡和纵坡度变化对弯沉试验数据造成影响。

4) 比对弯沉试验路段路表清洁无积水，尽量选在交通量较小的路段，保证测试过程稳定无其他交通的干扰。

选定某一沥青路面，标出所测路段及测点。激光动态弯沉系统分别以40 km/h、60 km/h、80 km/h的速度重复测试该路段，测试并输出所标记点的数据。贝克曼梁逐点采集所测试路段的数据。本次比对布置了15个测点，按照不同测试速度和不同测试方法，得到最终的弯沉测试数据分布如图3所示。

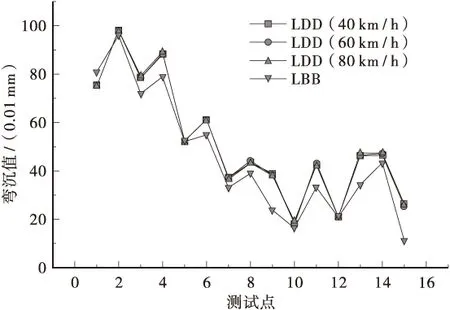
图3　弯沉测试数据

图3是激光动态弯沉系统和贝克曼梁测试的弯沉值分布图。从图中可以看出，激光动态弯沉系统和贝克曼梁测试有很好的相关性；其中激光动态弯沉系统分别以40 km/m、60 km/h、80 km/h测试弯沉数据重复性很好。在分析激光动态弯沉系统与贝克曼梁有很好的相关性的同时，接下来将进一步分析，在不同弯沉测试速度下与贝克曼梁的相关关系，并找出相关关系最匹配的速度值。

3.2激光动态弯沉回归分析

由图3可以看出激光动态弯沉系统与贝克曼梁测试数据大致分布在一条直线两边。相关关系显著，因此建立一元回归模型对不同速度下激光动态弯沉测试方法与贝克曼梁的弯沉测试比对数据进行回归分析，如图4所示，其各回归参数统计见表4和表5。

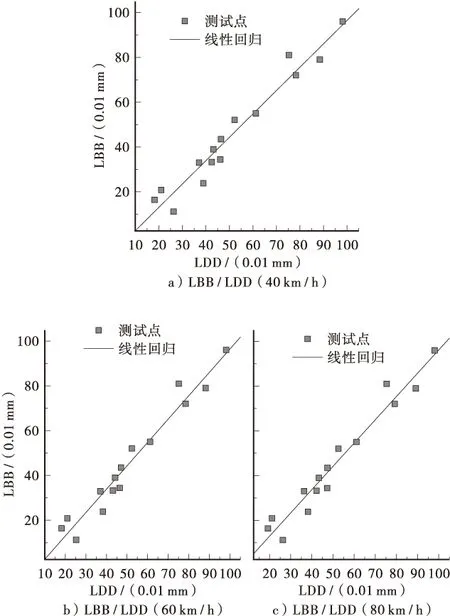
图4　不同速度下激光动态弯沉测试方法与贝克曼梁的　　　弯沉测试比对

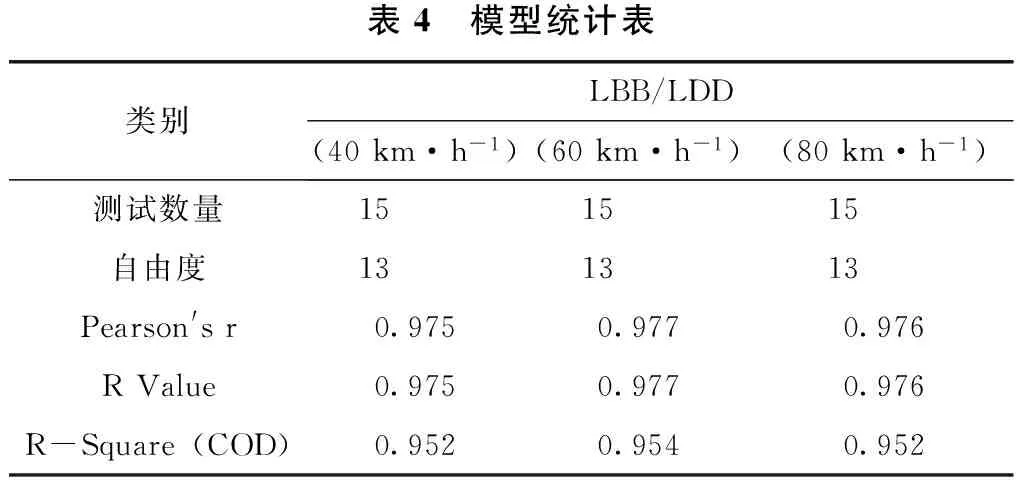
表4 模型统计表类别LBB/LDD(40km·h-1)(60km·h-1)(80km·h-1)测试数量15 15 15 自由度13 13 13 Pearson'sr0.9750.9770.976RValue0.9750.9770.976R-Square(COD)0.9520.9540.952

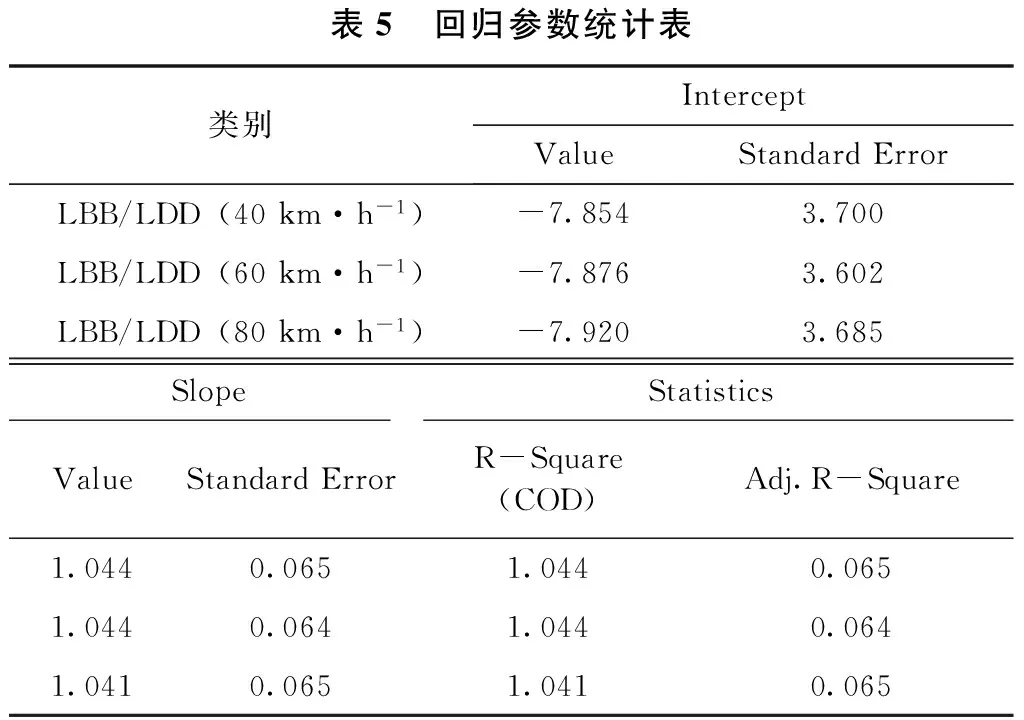
表5 回归参数统计表类别InterceptValueStandardErrorLBB/LDD(40km·h-1)-7.8543.700LBB/LDD(60km·h-1)-7.8763.602LBB/LDD(80km·h-1)-7.9203.685SlopeStatisticsValueStandardErrorR-Square(COD)Adj.R-Square1.0440.0651.0440.0651.0440.0641.0440.0641.0410.0651.0410.065

从表4的结果来看，3次试验回归的相关系数分别为0.975、0.977和0.976，，可知该模型能有效地解释激光动态弯沉系统与贝克曼梁弯沉仪的关系，拟合优度比较高，两者之间有较好的相关关系。

从回归模型的方差分析表6可以得出，40 km/h速度测试时的F统计量为255.321，对应的Prob>F值近似为0；60 km/h速度测试时的F统计量为269.634，对应的Prob>F值近似为0；80 km/h速度测试时的F统计量为257.829，对应的Prob>F值近似为0。根据上述数据，可以拒绝原假设，可知所建立的回归方程是显著的，满足检验要求。

从表7给出的回归参数统计表可以看出，对于常量(Intercept)：40 km/h速度测试时的t检验统计量为-2.123，对应的Prob>|t|值为0.044<0.05；60 km/h速度测试时的t检验统计量为-2.186，对应的Prob>|t|值为0.038<0.05；80 km/h速度测试时的t检验统计量为-2.149，对应的Prob>|t|值为0.041<0.05。对于变量(slope)：40 km/h速度测试时的t检验统计量为15.979，对应的Prob>|t|值近似为0；60 km/h速度测试时的t检验统计量为16.421，对应的Prob>|t|值近似为0；80 km/h速度测试时的t检验统计量为16.057，对应的Prob>|t|值近似为0。即，所有的t统计量是对应的Prob>|t|值不大于0.05，所在的显著性水平为0.05下，可以认为该回归方程满足t检验的要求。

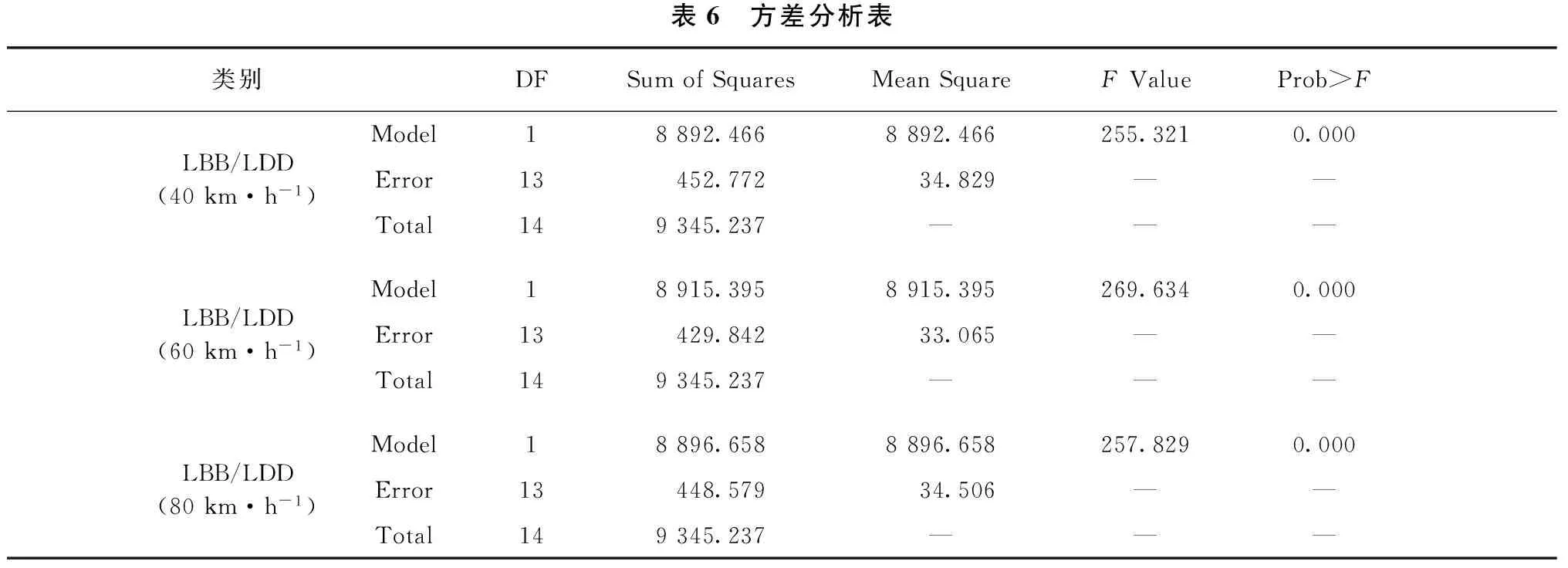
表6 方差分析表类别DFSumofSquaresMeanSquareFValueProb>FLBB/LDD(40km·h-1)Model18892.4668892.466255.3210.000Error13452.77234.829——Total149345.237———LBB/LDD(60km·h-1)Model18915.3958915.395269.6340.000Error13429.84233.065——Total149345.237———LBB/LDD(80km·h-1)Model18896.6588896.658257.8290.000Error13448.57934.506——Total149345.237———

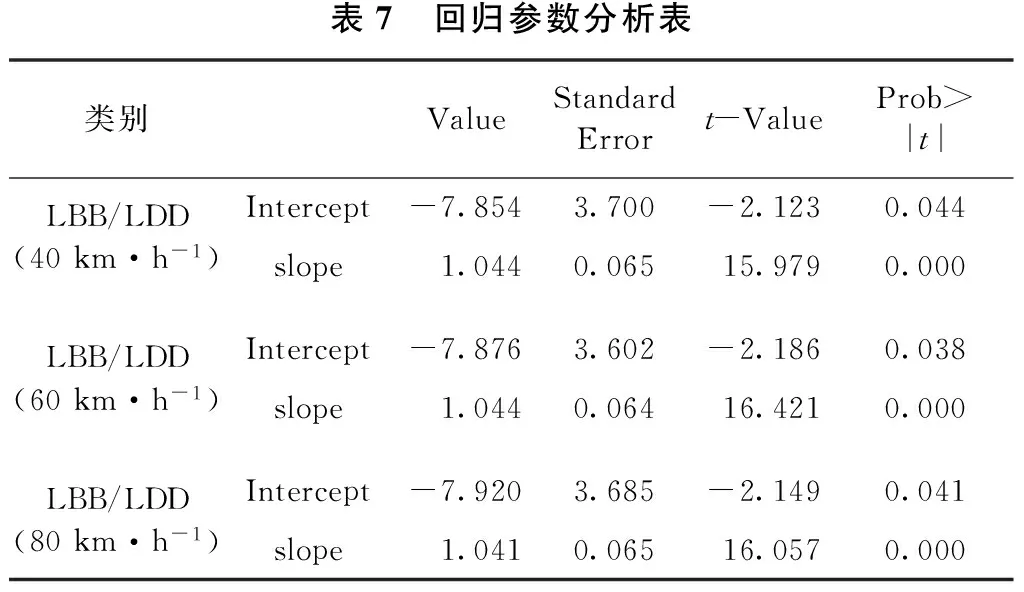
表7 回归参数分析表类别ValueStandardErrort-ValueProb>|t|LBB/LDD(40km·h-1)Intercept-7.8543.700-2.1230.044slope1.0440.06515.9790.000LBB/LDD(60km·h-1)Intercept-7.8763.602-2.1860.038slope1.0440.06416.4210.000LBB/LDD(80km·h-1)Intercept-7.9203.685-2.1490.041slope1.0410.06516.0570.000

只有当测试数据标定的相关系数达0.95以上才能建立可信关系[14]，故由表8可知：

1) 激光动态弯沉系统在相同的路面结构下采用不同的速度测试与贝克曼梁仪所测试的数据具有很好的相关性，相关系数分别为0.952、0.954、0.952达到规范的规定，有可信的数据关系。

2) 在其他试验条件相同的情况下，测试速度对于激光动态弯沉系统影响不大，在以60 km/h的速度进行测试时，与贝克曼梁仪的匹配性最好。

表8 不同测试速度下回归方程类别回归方程相关系数LBB/LDD(40km·h-1)LBB=1.044LDD-7.8540.952LBB/LDD(60km·h-1)LBB=1.044LDD-7.8760.954LBB/LDD(80km·h-1)LBB=1.041LDD-7.9200.952

3) 激光动态弯沉系统测试性能稳定，在不同的速度下进行测试，所得结果偏差不大。

4) 线性回归的斜率基本相同，而差异体现在截距上，这表明测试系统稳定，测试速度对截距有影响。

4结论

本文总结了激光动态弯沉测试技术适用性及其对传统测试技术的优势，分析了激光动态弯沉系统测试原理及其动态弯沉计算方法，基于激光动态弯沉测试技术开展了不同的测试速度与贝克曼梁的弯沉测试对比试验，得到以下主要结论：

1) 对于已建成，特别是运营多年的高速公路，由于施工、地质地形、交通流量、荷载等各种因素会影响路面弯沉的变化和发展趋势；对于激光动态弯沉测试系统，需将实测弯沉值进行温度修正，将温度影响因素降低到最小。

2) 激光动态弯沉系统测试性能稳定且测试速度和测试效率较快，所测试的弯沉数据是在真实的车辆荷载作用下，可连续地采集路弯沉测试数据，测试结果可靠，准确。

3) 激光动态弯沉系统在相同的路面结构下采用40 km/h、60 km/h、80 km/h的速度测试与贝克曼梁仪所测试的数据均具有很好的相关性，相关系数分别为0.952、0.954、0.952；在不同的速度下进行测试，测试速度对于激光动态弯沉系统影响不大，其60 km/h测试速度与贝克曼梁仪的匹配性最好，由于采用激光动态弯沉测试方法得到的数据更加全面，其评价结果更加精确。

参考文献：

[1] 孙志林，黄晓明.考虑层间接触的沥青路面非线性疲劳损伤特性分析[J].中南大学学报(自然科学版)，2012，43(6)：2385-2389.

[2] Castro M， Sanchez J A. Estimation of asphalt concrete fatigue curves：A damage theory approach[J].Construction and Building Materials，2008，22(6)：1232-1238.

[3] SUO Zhi，WONG W G，LUO Xiao-hui，et al.Evaluation of fatigue crack behavior in asphalt concrete pavements with different polymer modifiers[J].Construction and Building Materials，2012，7(1)：117-125.

[4] 陈长，孙立军，董茂强.基于现代检测技术的沥青路面评价新方法[J].公路交通科技，2006，23(9)：1-5.

[5] 王威.激光自动弯沉仪弯沉检测指标的研究[D].长沙：长沙理工大学，2013.

[6] 马涛.基于准直激光的路面回弹弯沉检测技术研究[D].西安：长安大学，2011.

[7] 邱欣，杨青，游庆龙.基于FWD动态弯沉盆参数的沥青路面模量反演分析[J].长安大学学报(自然科学版)，2013，33(6)：42-48.

[8] Hec M P.Use of FWD multi-load level data for pavement strength estimation[D].Raleigh：North Carolina State of University，2001.

[9] Goktepc A B，Agra E，Lav A H .Advances in back-calculating the mechanical properties of flexible pavements[J].Advances in Engineering Software，2006，37(7)：421-431.

[10] 张洪亮，胡长顺，许伟清.移动荷载下柔性路面的动力响应[J].长安大学学报(自然科学版)，2005，25(5)：6-10.

[11] Stefan A R，Metcalf J B.The errors in pavement layer module back-calculation due to improper modeling of layer interface condition[J].Journal of the Transportation Research Board，2003，1639(2)：36-42.

[12] 郑健龙.基于状态设计法的沥青路面弯沉设计标准[J].中国公路学报，2012，25(4)：1-9.

[13] Zaghloul S，Hoover T，Swan D J，et al.Enhancing backcalculation procedures through consideration of thickness variability[J].Journal of the Transportation Research Board，2004，1869(1)：80-87.

[14] JTG H20-2007，公路技术状况评定标准[S].

文章编号：1008-844X(2016)02-0001-06

收稿日期:2016-03-18

基金项目:国家自然科学基金项目( 51408060)

作者简介:武韬( 1990-) ，男，硕士，从事道路工程及岩土工程研究。

中图分类号：U 416.217

文献标识码：A