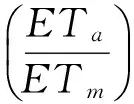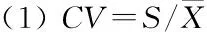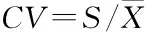基于Jensen模型的内蒙古河套灌区春玉米水分生产函数研究
侯 琼,王海梅,云文丽
(内蒙古生态与农业气象中心, 内蒙古 呼和浩特 010051)
基于Jensen模型的内蒙古河套灌区春玉米水分生产函数研究
侯琼,王海梅,云文丽
(内蒙古生态与农业气象中心, 内蒙古 呼和浩特 010051)
摘要:为了系统分析玉米整个生育期不同时期水分亏缺对产量的影响,适时开展灌溉影响评估,基于Jensen模型和水量平衡方程,利用水分试验数据和历史观测资料研究了河套灌区玉米水分敏感指数、玉米需水量和最高产量,建立了需水量和水分敏感指数时间变化方程,包括三项式和Logisitic两种形式,在旬尺度上二者的模拟结果十分接近;通过回代和实例检验,估算产量与实测产量有较好的一致性,回代结果的相关系数在0.92以上,相对误差小于15%的样本占到80%;实例检验的相关系数在0.63~0.69之间,相对误差低于20%的样本占到80%~100%,模拟效果基本符合实际。
关键词:水分敏感指数;Jensen模型;春玉米;需水量;水分生产函数;评估
作物水分生产函数反映作物产量随水量变化的规律,是进行灌溉经济效益分析和指导灌溉管理的基本依据[1]。最常用的形式有加法模型和乘法模型,通过数学模拟可以描述水分供应时间和数量对作物产量的影响程度[2-3]。乘法模型考虑了多阶段的相互影响,对总产量的反应灵敏度高[4],其中Jensen模型是国内外应用最为广泛的一种水分生产函数模型[5]。目前我国对冬小麦、水稻、夏玉米等作物的水分生产函数研究得比较深入,其中一些成果用于水资源经济模型计算并取得较好结果[6-10],为农业灌溉水资源优化分配和作物灌溉制度优化提供了理论依据和实践指导,但在产量预估方面的应用比较少见。
敏感指数是反映作物不同阶段缺水对产量影响程度的关键参数,其确认不仅与作物的抗逆性、生长发育阶段、作物和环境间的能量交换有关,还与水分试验设计的处理、水平组成等试验资料的代表性有关[11]。在以往的工作中,通常采用田间试验方法分不同发育阶段确定敏感指数,由于生育时段划分数量较少和时间间隔不统一,求出的水分敏感指数存在时域不稳定和缺乏可比性[12-13]等问题。丛振涛、韩松俊和王仰仁等[13-15]提出水分敏感指数累积函数的概念及计算方法,实现作物生长过程中水分敏感指数的变化模拟。但该方法的物理和生理机制认识不十分清晰,目前仍处于探索阶段[16],实际应用仍有难度。为了减少生育时段划分的非等距性和数量少对水分敏感指数时域不稳定性影响,提高作物水分生产函数的应用性,本文采取生育期等间隔细分的方法,根据田间水分试验资料,以10 d为时间尺度对Jensen模型的水分敏感指数进行了求算,基于作物的生育特性和积温原理,建立了水分敏感指数随时间变化的回归方程以及水分敏感指数的累积函数,并对两种方法计算的水分敏感指数进行了比较,通过试验和历史资料对回归方法计算的敏感指数和相关参数进行了验证,产量模拟效果基本符合实际,可用于河套灌区春玉米灌溉影响评估和优化灌溉制度的制定。
1材料与方法
1.1试验区基本情况
试验区位于巴彦淖尔河套灌区(40°45′N,107°25′E,海拔1 039.3 m),属中温带大陆性季风气候,光热资源丰富,年均日照时数3 084.6 h,年均气温8.7℃,干旱少雨,年降水量151.0 mm,雨热同季,6~8月降水量(93.0 mm)占全年降水量的61.6%,无霜期162 d。
1.2试验设计与数据来源
2013年4—9月在巴彦淖尔市农业气象试验站采用大型活动遮雨棚及池栽对春玉米(品种为郑单958)进行全程水分控制试验,小区面积24 m2,四周有2 m深度的防渗漏设施。试验设10个水分处理,分别在拔节~抽雄期和抽雄~乳熟期设置严重缺水、中度缺水、轻度缺水、水分适宜和偏湿5个等级(相应的土壤水分下限值分别控制为田间持水率的40%、55%、65%、75%和85%),非控水时段水分充分供给(田间持水率的75%~90%),其中包括整个生长季水分适宜和轻度偏旱两个处理,对照按常规灌溉,2次重复,共22个小区。根据各小区实测土壤水分(中子仪法测定)统计并计算一定深度的土壤相对含水率,拔节前和拔节后土壤水分控制深度分别为0~50 cm和0~80 cm土层,当土壤含水率达到控制下限时进行灌溉,灌溉方式为井灌,通过水表记录和控制灌水量。
播种时和出苗后,每5 d采用土钻法测定表层(0~30 cm)土壤含水率,利用中子仪法测定其它土层土壤水分,临近水分控制下限时进行加测,每隔10 cm为1层,测定深度2 m。在主要发育期(三叶期、拔节期、抽雄期、抽雄后20 d、乳熟期、成熟期)测定地上部分各器官干物质重;按照农业气象观测规范进行发育期观测和产量测定。
同时利用了1985—2011年历年玉米土壤水分逐旬观测值、发育期及产量等农业气象观测数据以及相应的气象资料,均来源于内蒙古气象信息中心。
1.3Jensen模型
Jensen模型是我国采用最为普遍的作物水分生产函数形式,其表达式[17]为:
(1)
式中,Ym、ETm分别为充分供水时的最高产量(kg·hm-2)和最大蒸散量(mm);Ya、ETa分别为缺水条件下的实际产量(kg·hm-2)和实际蒸散量(mm);n为生育阶段总数;i为生育阶段划分序号;λi为第i阶段缺水对产量影响的敏感指数,一般由试验资料确定,其值越大对产量的影响愈大,故λi值是Jensen模型的关键参数。
1.4蒸散量的计算
不同时段玉米需水量(最大蒸散量)和实际蒸散量采用水量平衡公式[18]计算,即:
ΔWi=Pi+Ii-ETai+Gi-ROi-Bi-Di
(2)
式中,ΔWi为时段开始和结束时土壤含水量的差值;Pi和Ii分别是时段降水量和灌溉量;ETai为实际蒸散量;Gi为地下水补给量;ROi为径流量;Bi为作物截留量;Di为渗漏量,单位均为mm。
通过对20个小区190~200 cm土层水分时间变化的分析,得出该土层水分的变化幅度在0.74~3.96 mm之间,平均为1.95 mm,变异系数CV平均为2.40%,在0.79%~5.96%范围内变化,说明该处水分通量变化很小,G、D参数可以忽略。由于在人工控制下(2)式中的RO和B基本不产生,也可以忽略不计,(2)式则可简化为:
ETai=Pi+Ii-ΔWi
(3)
1.5累积函数表达式
采用Logisitic生长曲线表示水分累积敏感指数随时间的变化过程
(4)
式中,λ(i)为水分敏感指数累积值;t为从出苗日算起的≥10℃相对积温,生长过程积温与总积温之比;K、a、b为待定系数,本文利用试验资料求算。
1.6模拟效果评价
利用平均绝对百分比误差(MAPD)、决定系数(R2)、平均相对误差(Wx)等指标检验和评价模拟效果。
总体误差采用MAPD评价指标,具体公式如下:
(5)
2Jensen模型有关参数的求算
2.1不同生产条件下最高产量Ym和需水量ETm的确定
作物需水量受作物品种和产量水平的影响,也会影响水分敏感指数λi。本文以水分适宜小区的产量(12 473.9 kg·hm-2)和蒸散量(604.2 mm)作为需水量计算样本,取整后产量水平为12 500 kg·hm-2,用Y-125表示,需水量为600 mm,用ETm-125表示。同时统计临河历年土壤水分、实际蒸散量和产量资料,选择旬土壤湿度均高于75%且高产年份的蒸散量,平均后作为临河地区玉米需水量,以及发育时段需水量,见表1。数据显示,临河地区试验产量和需水量略高于大田观测结果,可代表该地区最高产量和需水量。
以上述水分适宜小区和年份的数据为基础,采用(3)式计算逐旬需水量,以相对积温或相对生长期(阶段积温或发育天数占总积温或生育天数的比值)为时间变量绘制需水量变化图(见图1),并建立动态变化方程(表2)。不同产量水平下需水量的时间变化趋势十分相似,均表现为苗期少,随发育进程推进而增加,拔节~吐丝阶段达到最大值,吐丝~乳熟次之的变化规律。拟合方程时间变量的表达方式对方程的拟合效果无明显影响,相关指数R2均在0.95以上,为缩小品种和地区差异的影响,下文中的需水量以相对积温模型模拟计算。
注: LH-120表示临河12 000 kg·hm-2的产量水平。
Note: LH-120 indictes the 12 000 kg·hm-2yield level in Linhe.
2.2水分敏感指数的计算及变化特征
将试验得出最佳产量Ym、需水量ETm和各水分处理的实测产量Ya及由水分平衡方程计算的时段耗水量ETa,代入(1)式计算出苗到成熟期间逐旬水分敏感指数λ,λ值越大,表示相同缺水条件下造成的产量损失就越大[19]。水分敏感指数λ时间变化特征如图2,各阶段的λ差异很大,出苗~三叶期λ略高于三叶~七叶期,表明出苗前后水分亏缺会影响出苗率;三叶~七叶期玉米处于营养生长初期,植株矮小,叶面积小,是玉米的蹲苗期,水分亏缺对产量影响不大,λ值接近零;七叶期之后(相对积温0.2左右),特别是进入拔节期,植株茎叶生长迅速,幼穗快速发育,是营养生长和生殖生长并进阶段,需水量增多,水分亏缺对子粒的形成有很大影响,敏感指数迅速增加;在抽雄期趋于平缓,开花、吐丝期(相对积温0.65左右)达到最大值,并保持到灌浆初期,λ值达到0.1以上,玉米处于水分最敏感时期;灌浆中后期叶片开始衰老,气温下降,蒸腾降低,水分亏缺对产量形成的影响减小,λ逐渐减小,在相对积温0.9左右时,λ值为零;接近成熟期,λ出现不合理的负值,可做零处理,另一方面也表明水分过多不利于子粒脱水。λ的变化规律与玉米生长规律和水分生理特性十分吻合(图3)。
图3两种方法λ计算值的比较
Fig.3The comparision ofλvalues calculated by two methods
由于水分亏缺对作物产量的影响是一个连续的过程[13,15],为更好地表达玉米整个生育期不同时段水分亏缺对产量的影响,建立了λ随发育进程变化的模拟方程(表3),λ—Tx关系式的相关指数优于λ—t方程,λ—Dx关系式略差,其变化趋势与时间变量的表达形式无显著关系。
注:t、Dx和Tx含义同表2。
Note: The meaning oft,DxandTxwas similar with Table 2.
水分敏感指数累积函数是目前广泛应用的作物水分敏感指数求算方法[5]。基于试验资料求算累积函数(4)式的待定系数K、a、b分别为0.61、3.97和7.23,进而求出生长季旬水分敏感指数,并与三项式计算值比较,两组数据相关系数为0.971,前期差异很小,接近成熟时变大(见图3),t检验表明差异不显著(t=0.174 3模型参数的检验 3.1回代检验 直线回归分析表明,直线斜率都小于1,截距等于零时斜率有所提高,接近1,数据点分散于1∶1对角线的两侧,下方的点数多于上方,表明计算值小于实测值;相关指数相差很小(见图4),模型间无明显差异,回代效果比较理想。 3.2实例应用检验 依据临河历史资料确定的最高产量、需水量和λ积温模型值,运用农业气象观测资料(土壤水分、产量),采用上述方法计算各年实际产量,并与实测产量(地段测产)比较,结果显示,估算产量与实产之间相关程度较高,均达到0.01显著水平,但低于回代结果(表4)。直线回归图中的斜率α近于1,数据点较均匀地分散于对角线的两侧(图5),说明计算值小于或大于实测值的年份相近。 图4两种λ值计算产量与实测产量比较 Fig.4The comparison of calculated yield by two λvalues with the measured yield 为了验证最高产量确定的是否合理,选取最高产量相近值进行产量计算,结果表明,最高产量对计算结果有一定影响,但对趋势影响不大。从相关系数和误差中可以看出,估算产量与实测产量的相关系数均达到0.001的显著水平;MAPD为8.76~11.88%,波动较大;误差变异系数CV在0.57~0.75之间;平均相对误差低于15%的年份占到84.0~69.6%,Y-120效果最好(见表4),反映出最高产量的选择对估算结果有一定影响。总体上,本文确定的玉米水分敏感指数等相关参数及模拟计算方法比较合理,用于产量的估算是可行的。 4讨论和结论 基于Jensen模型估算作物产量取决于3个参数,即水分敏感指数λ、最高产量Ym和相应的需水量ETm,λ是关键影响因子。本文利用水分试验和历史观测资料,以试验和历史高产中确定的最高产量为目标函数,采用Jensen模型、水分平衡方程计算了不同产量水平下的玉米需水量、相对蒸散量和水分敏感指数,并建立了时间变化方程,通过水分试验和历史观测数据对Ya进行了回代和实例检验,得到以下分析结果: (1) 水分敏感指数在一定的气候环境下是相对稳定的,受产量水平的影响不显著,主要随生长发育阶段变化,用三项式拟合效果较好,即前期小,拔节后迅速增加,开花~灌浆初期达到最大,之后逐渐减小,与前人的研究结论一致[20-22]。同一种作物敏感指数的大小受生育阶段划分的影响,时段划分的越细,敏感指数越小[14]。本文以旬为时间尺度将玉米生长季划分为11个时段,等时段计算了水分敏感指数,利用建立的三项式和Logisitic时间变化方程计算了旬水分敏感指数,最大值0.11,两种计算结果十分接近,说明在旬尺度上二者具有通用性,其差异主要表现在开花以后,三项式计算的敏感指数在灌浆初期衰减的比较缓慢,灌浆后期较快,蜡熟期尽管出现不合理的负值,但已接近成熟可做零处理;而S曲线计算结果相反,灌浆初期下降较快,后期较慢,前者与玉米灌浆初期对水分仍十分敏感的生物学规律更为吻合。累积函数可实现λ日值的模拟计算,效果如何还有待于今后验证。 (2) 最高产量Ym和相应的需水量ETm在Jensen模型中是相对稳定的参数,对λ的确定和Ya的估算有重要影响。通过试验和历史观测资料确定的不同生产力水平下的最高产量和适宜需水量既考虑了水分限制因子,也涉及到土壤、品种、气候及管理水平等环境因子的影响,客观性比较强,需水量时间变化方程的建立可以动态模拟时段需水量,为实现产量动态评估提供依据。检验结果表明,本文确定的Ym和ETm有较好的适用性,可作为相关地区的参考。 (3) 利用相对积温或相对发育日期建立的λ1关系模型可以消除品种和气候波动的影响,增强应用的普适性。通过试验数据回代和实例计算,运用确定的Jensen模型参数估算的产量Ya与实际观测产量的一致性较好,回代结果的r在0.92以上,相对误差小于15%的样本占到80%左右;实例检验r在0.63~0.67之间,相对误差低于20%的样本占到82.6%~100%,总体上模拟效果可以满足实际需要。 (4) 实际蒸散量的计算有两种方法,一是水分平衡实测法,二是作物系数法,本文是利用水分平衡实测法计算的,在实际应用中作物系数法应用最普遍,也更为便捷,用作物系数法替代后的结果如何,还需要深入研究。 参 考 文 献: [1]杨旭东,白云岗,张江辉,等.塔里木盆地棉花水分生产函数模型研究[J].南水北调与水利科技,2008,4(6):110-112. [2]山仑,康绍忠,吴普特.中国节水农业[M].北京:中国农业出版社,2004:150-155. [3]金建华,孙书洪,王仰仁,等.棉花水分生产函数及灌溉制度研究[J].节水灌溉,2011,(2):46-48. [4]张恒嘉.几种大田作物水分-产量模型及其应用[J].中国生态农业学报,2009,17(5):997-1001. [5]韩松俊,王静,刘群昌,等.三种作物水分生产函数模型的适用性比较[J].灌溉排水学报,2009,28(4):10-13. [6]肖俊夫,刘战东,陈玉明.中国玉米需水量与需水规律研究[J].玉米科学,2008,16(4):21-25. [7]王克全,付强,季飞,等.黑龙江省西部半干旱区水稻水分生产函数及优化灌溉制度研究[J].节水灌溉,2007,(8):48-51. [8]罗遵兰,冯绍元,左海萍.山西省冬小麦水分生产函数模型初步分析[J].灌溉排水学报,2005,24(1):16-19. [9]肖俊夫,刘战东,段爱旺,等.中国主要农作物全生育期耗水量与产量的关系[J].中国农学通报,2008,24(3):430-434. [10]付强,王立坤,门宝辉,等.三江平原井灌水稻水分生产函数模型及敏感指数变化规律研究[J].节水灌溉,2002,(4):1-3,42. [11]陈亚新.作物—水模型及其敏感指标的确认[J].灌溉排水,1995,14(4):1-6. [12]沈荣开,张瑜芳,黄冠华.作物水分生产函数与农田非充分灌溉研究评述[J].水科学进展,1995,(3):248-254. [13]丛振涛,周智伟,雷志栋.Jensen模型水分敏感指数的新定义及其解法[J].水科学进展,2002,13(6):730-735. [14]韩松俊,刘群昌,王少丽.作物水分敏感指数累积函数的改进及其验证[J].农业工程学报,2010,26(6):83-88. [15]王仰仁,雷志栋,杨诗秀.冬小麦水分敏感指数累积函数研究[J].水利学报,1997,(5):28-35. [16]张文华,张翔.一种新S曲线的建议[J].数学的实践与认识,2005,35(6):202-205. [17]Jensen M E. Water consumption by agricultural plants[C]//Kozlowski T T. Water Deficit and Plant Growth. New York: Academic Press, 1968. [18]康绍忠.农业水土工程概论[M].北京:中国农业出版社,2007:460-480. [19]欧定华,夏建国,张莉,等.多作物种植结构和灌溉水量优化模型及算法研究[J].中国生态农业学报,2013,21(12):1515-1525. [20]范雅君,吕志远,田德龙,等.河套灌区玉米膜下滴灌灌溉制度研究[J].干旱地区农业研究,2015,33(1):123-129. [21]西北农业大学农业水土工程研究所,农业部农业水土工程重点开放实验室.西北地区农业节水与水资源持续利用[M].北京:中国农业出版社,1999:131-135. [22]樊廷录,杨珍,王建华,等.灌水时期和灌水量对甘肃河西玉米制种产量和水分利用的影响[J]. 干旱地区农业研究,2014,32(5):1-6. Research on water production function of spring maize in Hetao Irrigation District (ID) of Inner Mongolia based on Jensen model HOU Qiong, WANG Haimei, YUN Wen-li (EcologicalandAgriculturalMeteorologicalCenterofInnerMongolia,Hohhot,InnerMongolia010051,China) Keywords:water sensitive indexes; Jensen model; spring maize; water requirements; water production function; assessment Abstract:In order to systematically analyze the effects of water deficit in different growth stages to the yield of maize in whole growth period, carried out the assessment on timely irrigation. Based on the Jensen model and water balance equation, using the moisture test data and history mearured information, researched the water sensitive index, water requtrements and maximal yield of maize in Hetao ID, established the time change equation of water requirements with the water sensitive index, inclued two forms as Three Parameters Formular and Logistic Equation, on 10 days scale, the simulated results by both of them were very close. Through the back and instance test, there was a good consistence between estimated yield and measured yield, the correlation coefficient of return result was above 0.92, the samples with relative error less than 15% were accounted for 80%. The correlation coefficients tested by the instances were between 0.63 to 0.69, the samples with relative error less than 20% were accounted for 80% to 100%, the simulated results were basically conformed to the reality. 文章编号:1000-7601(2016)03-0084-06 doi:10.7606/j.issn.1000-7601.2016.03.13 收稿日期:2015-05-22 基金项目:国家公益性行业(气象)科研专项(GYHY201206021) 作者简介:侯琼(1960—),女,河北行唐人,正研级高工,主要从事节水灌溉预报技术和旱灾研究。E-mail:nmg-hq@qq.com。 中图分类号:S512.1+2;Q945.17 文献标志码:A