Multi-Band Texture Image Fusion Based on the Embedded Multi-Scale Decomposition and Possibility Theory

LIN Su-zhen, WANG Dong-juan, WANG Xiao-xia, ZHU Xiao-hong

School of Computer and Control Engineering, North University of China, Taiyuan 030051, China

Multi-Band Texture Image Fusion Based on the Embedded Multi-Scale Decomposition and Possibility Theory

LIN Su-zhen, WANG Dong-juan, WANG Xiao-xia, ZHU Xiao-hong

School of Computer and Control Engineering, North University of China, Taiyuan 030051, China

The combination of multi-scale transform and the rules which are “high-frequency coefficients combined by selecting the maximum gray value or energy” and “low-pass ones combined by weighting average” is an effective method in dual-band image fusion. However, when these methods are used to fuse multi-band images, sequential weighted average often leads the weakening of the inherent different information of original images, which affects the subsequent target recognition and scene understanding. The problem is more obvious when fusing multi-band images with texture features. In order to describe the scene in a more comprehensive and precise way, a new multi-band texture image fusion method based on embedded multi-scale decomposition and possibility theory is proposed. The method consists of three parts. The original multi-band images are decomposed into their high- and low-frequency components through a multi-scale transform. The high-frequency components are fused per-pixel by extracting the maximum gray value, whereas the last layer of low-frequency components of original multi-band images with the largest standard deviation is blocked through the another multi-scale transform. Based on the specific sizes and positions of these blocks, the remaining two original images are divided. All the blocks from three bands are traversely fused according to the possibility theory, and the low-frequency image is formed by mosaicing these fused blocks. Then, this image is inversely transformed with its high-frequency counterparts to get the final fusion image. This method not only integrates the pixel-level with feature-level fusion methods, but also integrates the space domain with transform domain technologies together, and solves the problem of sawtooth effect on the edge of the target through the different fusion rules with the different sizes of blocks. The validity of the method proposed is proved.

Image fusion; Multi-band texture image; Embedded multi-scale decomposition; Possibility theory

Introduction

The multi-band imaging is used to get a more comprehensive and precise description of the scene by highlighting the differences and complementarities of the detection results in different wave bands[1]. For example, the long wave infrared has better penetration in smog and vision in low temperature and darkness when compared with medium and short long wave infrared. But the medium wave infrared has advantages in the detection of the high humidity condition. As for the short wave infrared, it enjoys an obviously stronger resolution than the other two, but the ability of night vision in complete darkness is much less than the medium wave and long wave[2-3]. Often it is convenient to merge such multi-band images into one composite representation for interpretation purposes[4]. Known as image fusion, this combination technique is a promising research area.

It is now generally accepted that the combination of multi-scale transform and the rules which are “high-frequency coefficients combined by selecting the maximum gray value or energy” and “low-pass ones combined by weighting average” is an effective method. The ideal effect can be obtained in dual-band fusion image with this method. However, with the development of multispectral and hyperspectral detection, it is imminent to meet the need of fusing multi-band images. The different information among the source images will be weakened in the fused image through this weighted average or sequential weighted average. And the more the detected bands are, the worse the situation is[5]. To address this problem, our team attempted to fuse structure images by choosing blocks in the spatial domain using Quadtree (QT), and we had achieved some effects[6]. But the fusion effect was not satisfactory for the texture images, such as tree, grass, etc. Not only is blocking running time long, but also the fused result is not ideal due to the sawtooth of the edge.

To improve the situation, this paper takes the texture images of the three wave bands (SWIR/visible light and MWIR, LWIR)as targets to conduct the following experiment. Quadtree is embedded in the process of support value transform (SVT). Then the two multi-scale transform integrate with the fusion rules of multi-source information possibility theory to produce a good fusion result. In addition, all input images are assumed to be adequately aligned and registered prior to fusion process.

1 Proposed Method

This paper proposes the multi-band images fusion method based on embedded multi-scale decomposition (EMD) and the possibility theory as shown in Fig. 1. First the multiband texture images are decomposed by multi-scale decomposition. Then the shortwave low-frequency image with the largest standard deviation is blocked in space domain. Based on the specific sizes and positions of these blocks, the remaining two bands of original images are divided correspondingly. All the blocks from three bands are traversely fused according to the possibility theory, and the low-frequency image is formed by mosaicing these fused blocks. Then, this resulted image is inversely transformed with its high-frequency counterparts to get the final fusion image.

Fig.1 Schematic diagram of multi-band texture images fusion framework

2 Algorithm Realization

2.1 Embedded Multi-scale Decomposition

It is suggested that the fused images of multi-scale transform have ringing effect and shift-variant except NSCT, DTDWT, UWT and SVT[7-8]. Particularly in SVT, only the last layer of low-frequency components is needed when the inverse transform is conducted. This successfully simplifies the calculation, increases the speed, and facilitates the secondary multi-scale decomposition. Therefore, the current study chooses SVT to conduct the first multi-scale decomposition. QT is selected here because of its effectiveness in extracting the local properties of the target. For the convenience, the following are descriptions of focusing on SWIR, MWIR and LWIR with texture as the main characteristics.

2.1.1 Support value decomposition

The SVT method is as follows and more detailed information can be found in [9].

(1)

whererstands for the decomposition level,Sjis the sequential support value images,Pis the original input image,Pjrefers to the sequential low-frequency components, andSVjrepresents the sequential support value filters. The initial filter commonly refers to the Gaussian radial basis kernel function and can be made into the sequential support value filters by filling zero every other row and every other column.

2.1.2 Quadtree decomposition

(3)Repeating the following operation for each block at levell.

2.2 Fusion Rules

2.2.1 Feature-level fusion

Since the texture information in the SWIR images are clearer than those of the other two bands, images of this band are always chosen to fuse the small blocks. While fusing large blocks, images of MWIR and LWIR become the ideal choice for their high contrast ratio, which are formed by the difference between targets and backgrounds. It is worth noticing that the differences between the corresponding blocks of the multi-band images are the precondition of image fusion, whether these differences exist and how big they are can only be estimated, namely only a kind of possibility. The multi-source information possibility theory holds that when the difference between various sources is big, the disjunctive form can be chosen to get a better fusion results[10]. Therefore, the feature-level fusion includes the following two types of rules:

(2)

(3)

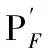
2.2.2 Pixel-level fusion

This rule is extracting of maximum gray value which used to fuse the high-frequency components, the results are the fused sequential support value imagesSFj.

2.3 Support Value Inverse Transformation

(4)

wherePis the final fusion image.

3 Analysis of the Elements Affecting the Experiment

The experiment subjects are the texture images, as shown in Fig.4(a), (b) and (c)[11].

3.1 Effect of EMD on Fusion Results

Here, in Fig.2, the edge intensity, contrast ratio and local standard deviation are chosen as the related indexes to evaluate the fused result.

Fig.2(a) shows the different edge intensities of EMD and QT fused images under differentTwheng=1. When T changes between 0.08 and 0.4, the intensities of the former are between 64.58 and 66.0 while those of the latter are between 35 and 36.3. The large edge intensity is favorable to identify the target, therefore, the former is superior to the latter.

Fig.2(b) shows the dynamic curves of the contrast ratio after EMD and QT with the former changing from 150.0 to 152.1, and the latter from 93.6 to 94.8. The contrast increase is of benefit to the visual observing or automatic target recognition, thus the former is better than the latter.

Fig.2(c) shows the different local standard deviations (LSTD) of these two methods with the size of the local window being 5×5. One is between 24.6 and 25.4, and the other is between 13.4 and 14.1. The bigger the local standard deviation is, the richer the image information. This illustrates that more information can be received from the fusion of EMD than from that of QT.

Fig.2(d) shows the different running time. The former is 17.5 times shorter than the latter on the average. It shows that the fusion of EMD just runs at a higher speed than that of QT.

3.2 Effect of g

Fig.3 shows the changes of the edge intensity, contrast ratio, sharpness and local standard deviation with EMD whenT=0.08 and the size of blocks is 2g. Wheng=1 or 2, the result is better, butgis certainly affected byT.

Fig.2 Comparison of indexes of fused images by EMD and QT

Fig.3 Curves of parameters with blocking criteria g by EMD

4 Analysis of the Experiment Result

4.1 Subjective Analysis

Fig.4 (a), (b) and (c) are the SWIR, MWIR and LWIR images respectively. The treetop, car and ground in Fig.4 (a) are the most distinctive in the three images. The person, the small target (in the dashed box) hidden in the treetops and the front tire of the car in Fig.4 (b) are clearer than those in Fig.4 (a). The person, the another small target (in the dashed box) hidden in the treetops and the front tire of the car in Fig.4 (c) are clearest among the three images. The fusion task, thus, is to merge the clearest information in the three images.

Fig.4 (d), (e) and (f) are, respectively, the fused result of QT, SVT and EMD (T=0.20 andg=1). The subjective observation shows that the ground texture, person, car and two small targets hidden in the treetop in Fig.4 (f) are more distinctive than those in Fig.4 (d) and (e). Except for a clear treetop texture, the other objects demonstrated in Fig.4 (d) are all dimmer and affected by an obvious mosaic effect.

Fig.5 shows another experiment images[11]. They are the images of visible light, MWIR and LWIR, and fused image by QT, SVT and EMD, respectively.

4.2 Objective Analysis

In this analysis, the edge intensity, contrast ratio, local standard deviation and running time are chosen as indexes of evaluation. The former two are calculated in the following way.

Fig.4 No.1 Multi-band images used in the experiment

Fig.5 No.2 Multi-band images used in the experiment

(1) Edge intensity

Assume thati,jandkstand for the row, column and dimension of the image, respectively. The size of the filter ism×n. First, the fused imagePis filtered to extract the edge information.

(5)

whereWis “Sobel ” operator,M=1 andN=1.

The gradient of the image is

(6)

Then the average gradient is calculated which is the edge intensity.

(2) The contrast ratio of the target to background is calculated by Eq. (7).

(7)

whereμtandμbare, respectively, the average gray value of the target and background, got through automatic threshold segmentation.

Table 1 lists the calculation results of the objective evaluation indexes. The calculation parameters areT=0.20 andg=1. The decomposed level of SVT is 4. The result shows that, compared with the average results of QT and SVT, EMD increases the edge intensity by 37.37%, the contrast ratio by 836.93% and the local standard deviation by 27.04%. It decreases the running time by 54.55% in the mean time. The change rate of indexesr, is average result ofr1andr2which calculated by Eq. (8).

(8)

whereμEMD,μSVTandμQTare respectively the related indexes of the fused images of EMD, SVT and QT. Subscript 1 and 2 are experiment images of the first and second groups, respectively.

The operation environment of the experiment: CPU is Intel Core(TM)i5-2450 and 2.50GHz; internal storage is 2GB, the system is windows 7 and programming language is Matlab R (2007) b.

Table 1 Comparison of indexes in different methods

5 Conclusion

A novel image fusion approach based on EMD and possibility theory is presented in this paper. QT is embedded in the process of SVT. And according to the different sizes of blocks, different fusion rules are used based on the multi-source information possibility theory. It successfully solves the problem of weakening inherent information difference caused by weighing average fusing multi-band texture images and the sawtooth effect on the edge of the target. Our method can have not only the advantages of pixel-level and feature-level fusion, but also the benefits of transform and spatial domains fusion methods.

Acknowledgments： We sincerely thank the reviewers and editors for carefully checking our manuscript.

[1] Cetin A E, Dimitropoulos K, Gouverneur B. Digital Signal Processing, 2013, 23(6): 1827.

[2] Rogalski A. Progress in Quantum Electronics, 2012, 36(2-3): 342.

[3] Yuhendra, Alimuddin I, Josaphat T S, et al. International Journal of Applied Earth Observation and Geoinformation, 2012, 18: 165.

[4] Gangapure V N, Banerjee S, Chowdhury A S, et al. Inf. Fusion, 2015, 23: 99.

[5] Ellmauthaler A, Pagliari C L, DaSilva E A B. IEEE Transactions on Image Processing, 2013, 22(3):1005.

[6] Lin S Z, Zhu X H, Wang D J, et al. Journal of Computer Research and Development, 2015, 52(4): 952.

[7] Jiang Y, Wang M H. Inf. Fusion, 2014, 18: 107.

[8] Adu J H, Gan J H, Wang Y, et al. Infrared Physics & Technology, 2013, 61: 94.

[9] Yang F B, Wei H. Infrared Physics & Technology, 2013, 60:235.

[10] Ji L N, Yang F B, Wang X X, et al. Optik, 2014, 125(16): 4583.

[11] Fay D A, Waxman A M, Aguilar M, et al. Proceedings of the 3rd International Conference on Information Fusion, 2000, 1: TuD33.

TP391

A

基于嵌入式多尺度分解和可能性理论的多波段纹理图像融合

蔺素珍, 王栋娟, 王肖霞, 朱小红

中北大学计算机与控制工程学院，山西 太原 030051

将多尺度变换和“高频取大、低频加权平均”融合规则相结合是融合双波段图像的有效方法。但用该类方法融合多波段图像时，序贯式加权常常会导致原图像间固有的差异信息在融合图像中被弱化，从而影响后续的目标识别和场景理解。该问题在融合具有纹理特征的多波段图像时更为突出。为此，提出了一个基于嵌入式多尺度分解和可能性理论的多波段纹理图像融合新方法。首先，利用一种多尺度变换方法把多波段原图像分别分解为高频和低频成分，并对多波段图像中标准差最大的一幅原图像的低频成分利用另一种多尺度方法进行分块，再以该分块图像的大小和位置为标准对其余波段的原图像进行分块。然后，基于可能性理论的相关融合规则逐一融合对应的多波段块图像，再把块融合图像进行拼接，以拼接结果作为低频融合图像。最后，将该低频融合图像和利用取大规则融合得到的高频成分一起通过多尺度逆变换获得最终的融合图像。这种方法不仅将像素级和特征级融合方法综合在一起, 而且将空间域和变换域技术综合在一起, 并通过对大小块采用不同融合规则解决了目标边缘的锯齿效应问题。实验表明该方法效果显著。

图像融合； 多波段纹理图像； 嵌入式多尺度分解； 可能性理论

2015-06-02，

2015-10-11)

Foundation item： National Nature Science Foundation of China (61171057)，Nature Science Foundation of Shanxi Province of China (2013011017-4)

10.3964/j.issn.1000-0593(2016)07-2337-07

Received： 2015-06-02; accepted： 2015-10-11

Biography： LIN Su-zhen, (1966—)，female, professor in School of Computer and Control Engineering, North University of China e-mail: lsz@nuc.edu.cn