基于偏振菲涅尔反射比分布的主动偏振成像目标辨别方法

耿利祥, 陈 钱, 钱惟贤, 顾国华, 潘佳惠

1. 南京理工大学电子工程与光电技术学院441教研室，江苏 南京 210094 2. 南京理工大学江苏省光谱成像与智能感知重点实验室，江苏 南京 210094

基于偏振菲涅尔反射比分布的主动偏振成像目标辨别方法

耿利祥1, 2, 陈 钱1, 2, 钱惟贤1, 顾国华1, 潘佳惠1

1. 南京理工大学电子工程与光电技术学院441教研室，江苏 南京 210094 2. 南京理工大学江苏省光谱成像与智能感知重点实验室，江苏 南京 210094

由于偏振特性是材料自身所决定的物理特性，其偏振图像含有丰富的目标信息，利用偏振信息对目标进行识别一直是国内外目标探测领域的研究热点，而主动偏振成像较之被动偏振成像更具有信噪比高以及可控性好等优势。在详细分析了偏振菲涅尔反射比分布的理论基础上，提出了一种利用探测物体表面的偏振菲涅尔反射比的主动偏振成像方法。该方法在发射端将偏振方向正交的两种偏振态的光源交替照射到目标场景中，在探测端用分别装有两个偏振方向垂直的偏振片的CCD采集偏振图像。同时，将探测端架构在不同的探测方向采集目标经主动光源照射后的偏振数据，最后将这些数据传输到计算中心，通过最优化拟合技术反演出不同目标的光学常数，由于不同目标的表面材质不同，其反映出的光学常数就不同，从而达到辨识不同材质目标的目的。实验分别采用了仿真数据和实测数据来验证该方法的有效性。仿真实验显示，所提出的方法利用材料的光学常数对不同材料进行区分不仅是科学的而且更方便有效。实测数据进一步验证了该方法能够较好的恢复出目标的相关光学常数，尤其在区分金属和非金属材料方面表现突出，并且探测方法结构简单实用，在目标探测、伪装识别等领域中有较大应用前景。

主动偏振探测； 偏振菲涅尔反射比； 双向分布反射函数； 偏振成像

引 言

对于成像目标探测系统而言，偏振信息作为目标新的一维信息，是目标表面的一种基本的光学特性，目标的偏振特性与目标的材料、目标表面形态、目标表面粗糙度等都有关系。主动偏振成像由于发射的光的偏振态等调制信息已知，所以在接收到的偏振图像后能够更准确的反推出目标的表面特性。Martin Laurenzis[1]等对主动偏振探测系统的照明激光光源的设计和应用做了详细研究，目的在于得到强度均匀没有光斑的照明环境。Daniel A LeMaster[2]等采用了短波红外激光作为主动光源，在夜间环境下，通过得到的红外计算出目标的部分穆勒矩阵，从而达到区分目标的目的。国内黎全[3]等利用了表面散射光偏振差异来进行目标识别，文献[4-5]对激光偏振主动成像的实验方法进行了改进和优化。然而由于偏振特性其本身的机理较为复杂，尤其是对粗糙的目标表面建模。目前对物体表面散射光分布研究较为流行的是偏振双向分布反射函数，该模型自Priest等提出以来得到了广泛的发展[6-9]。本文在此模型的基础上，采用偏振光作为主动光源，照射到物体后在其表面发生散射，通过不同探测角度上探测到的偏振图像信息来辨识不同材料的目标。

1 双向分布反射函数(bidirectional reflectance distribution function, BRDF)理论

双向反射是指地物的反射率随入射方向和反射方向而变化的特性。如图1所示，在样品表面建立笛卡尔三维坐标系。

θi和θr分别为入射和探测方向的天顶角，φi和φr分别为入射和探测方向的方位角。根据文献[6-7]中定义，BRDF的物理意义是经样品表面反射在探测方向(θr,φr)产生的辐射亮度与入射方向(θi,φi)入射到样品表面上的辐照度的比。即

(1)

微面元BRDF模型是假设物体的粗糙表面是一系列微小面元的集合，对于整个平面而言，探测到的辐射亮度是由一系列微面元的分布的宏观反映。因此标量微元面BRDF模型[6]可以表示为

(2)

式中σ2表示表面粗糙度的斜度方差，F(β)表示菲涅尔反射系数。θ表示微面元法线与样品表面法线之间的夹角，β表示微面元的入射角或探测角。

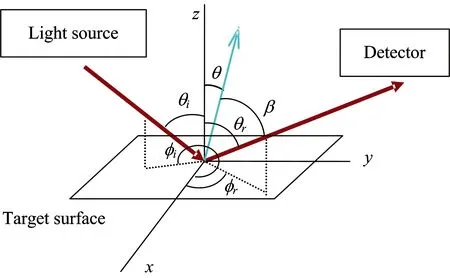
图1 BRDF坐标系统

2 偏振菲涅尔反射比分布测量

目标对偏振态垂直和平行于反射面的偏振光的菲涅尔反射率分别为Fp和Fs，并且假定对应入射光的光强分别为Ip和Is，那么经过镜面反射之后这两种光的光强应该分别为FpIp和FsIs。对于粗糙物体表面应用BRDF模型，两种光的光强就为fpIp和fsIs。

假定探测端的偏振片的偏振角为ω，那么由对应探测到的偏振光光强分别为fpIpcos2ω和fsIpsin2ω。由于采用的光源相同，p光和s光的光强相等，即Is=Ip=I，并且考虑到漫反射成分Id的存在，那么反射到探测端的光强为

(3)

探测部分利用两个CCD探测器，分别装有偏振角为ω0度和ω90度的偏振片，其中ω90=ω0+90°。那么当p光入射时，两个探测器分别探测到的光强为

(4)

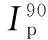
(5)

由文献[10]中定义偏振菲涅尔系数比PFR(polarization fresnel ratio)为

(6)

该定义是基于光滑表面的镜面反射，对一般粗糙物体表面，利用物体表面双向分布反射函数(BRDF)模型分析。所以目标的偏振菲涅尔系数比可以表示为

(7)

可以发现，当P光和s光分别入射目标表面时，目标的探测角度、粗糙度、目标表面法向和微面元法向夹角都是不变的，目标的散射分布函数系数可以被约掉，偏振菲涅尔系数比可以由以上四组数据直接得到，而与目标本身的散射光分布没有关系。

3 目标材料的光学常数的计算

物体目标表面的菲涅尔反射系数通常是由物体表面材料的复折射率决定的，复折射率一般表示为η=n+ik，其中n表示折射率，k为衰减系数。由文献[11]可知，复折射率和菲涅尔系数的关系有

(8)

其中

由此可以看出，Fp和Fs都是角度β的函数，因此偏振菲涅尔系数比也是β的函数，其可以表示为

(9)

在测量得到多个方向的PFR的时候，PFR的分布应该满足上式，因此构造目标函数

(10)

式中：m表示m个不同的测量角度，Qi表示第i次测量对应角度下的理论偏振菲涅尔系数比(PFR)，qi表示第i次测量对应角度下的实测偏振菲涅尔系数比。

那么求n和k就转化为要求使得目标函数最小时候的参数n和k，即

[n, k]=argminG(n, k)

(11)

最终采用非线性最小二乘拟合算法，求得最优参数n和k。

4 实验数据处理及分析

4.1 仿真实验分析

实验仿真了不同材料光学常数的偏振菲涅尔系数比(PFR)随探测角度变化的曲线，并且仿真了在不同角度下，材料光学常数不同而引起探测的材料的反射偏振光的不同。

如图2所示，仿真两种材料(n=2 ，k=0.4)和(n=1.2，k=0.2)，两种材料的PFR曲线在探测角度越靠近于零度(<30°)的地方越相似，其区分度并不高[图2(a)]，而在30°～80°的区间内区分度比较明显[图2(b)和(d)]。然而在区分度较高的区间内，当探测角为57°左右时，两种材料的PFR也是相近的[图2(c)]，所以用单个探测角度的数据来进行目标的识别是缺乏辨识能力的。通过探测到材料在这条曲线上的多个点的值，然后反演出材料的光学常数，再通过材料的光学常数对不同材料进行区分不仅是科学的而且更准确有效。

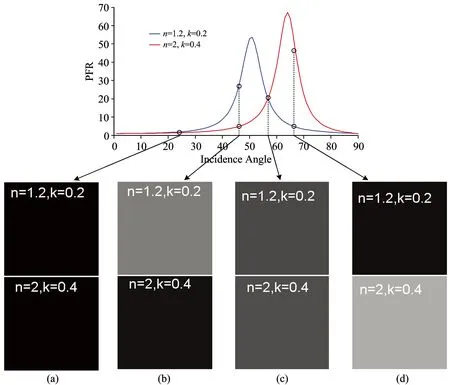
图2 仿真实验结果偏振菲涅尔系数比(PFR)随探测角度变化的 曲线图以及相关探测方向PFR对应的灰度图

4.2 测量数据及分析

实验对普通大理石采集了若干不同方向的偏振数据，每个方向即为对应一个角度β，β仅由主动光源入射方向和探测器的方向决定，因此β角的测量由光源和探测器的经纬仪测量得到，实验中主动光源的波长为630 nm。对于每个β角，对应每个探测方向就能探测得到四个不同的图像，利用式(7)计算得到每个方向的偏振菲涅尔系数比PFR，如表1所示。通过非线性最小二乘算法，将数据拟合得到如图3所示曲线，拟合得到的曲线参数为n=1.493 8，k=0。

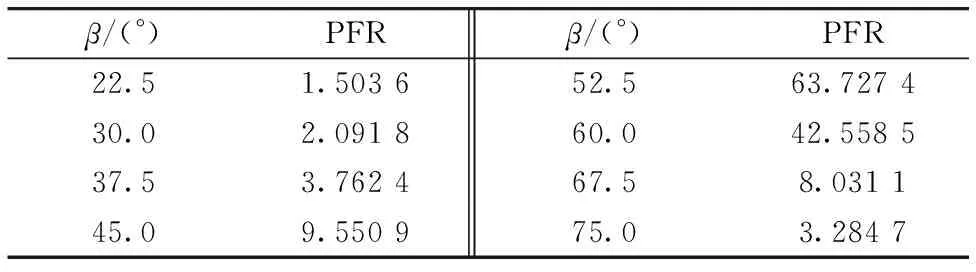
表1 大理石不同探测方向的偏振菲涅尔系数比PFR

从图3中可以看出，由于大理石是绝缘材料，因此其消光系数k为0，在接近60°的地方会出现布鲁斯特角，其PFR曲线在布鲁斯特角的地方会非常大，因而造成其严重的非线性，为了减少这种非线性的影响，实验中采用了偏振菲涅尔系数比PFR的倒数绘制了相应的曲线来进行参数拟合，如图3(b)。

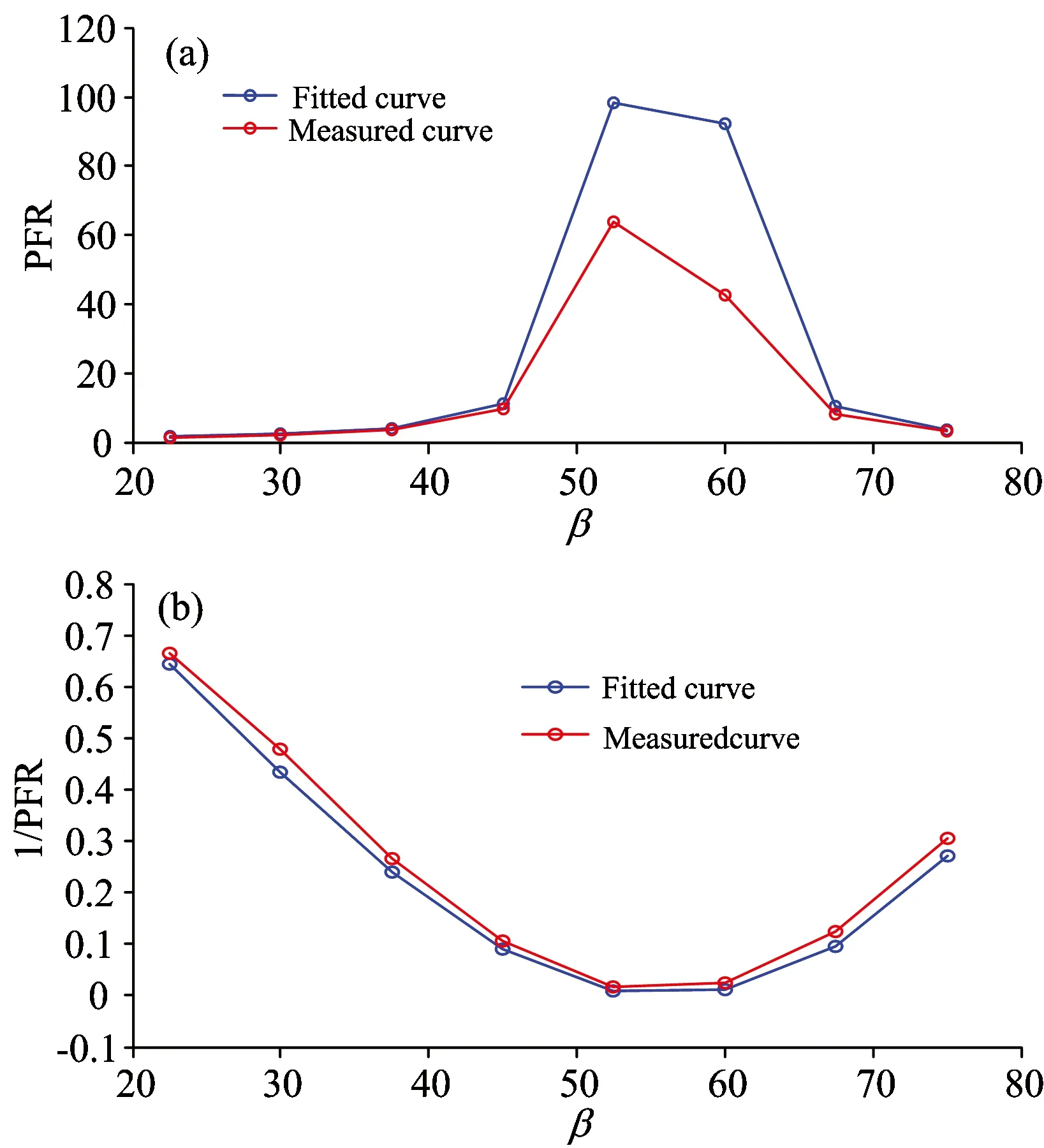
图3 大理石不同探测方向的偏振 菲涅尔系数比PFR拟合曲线

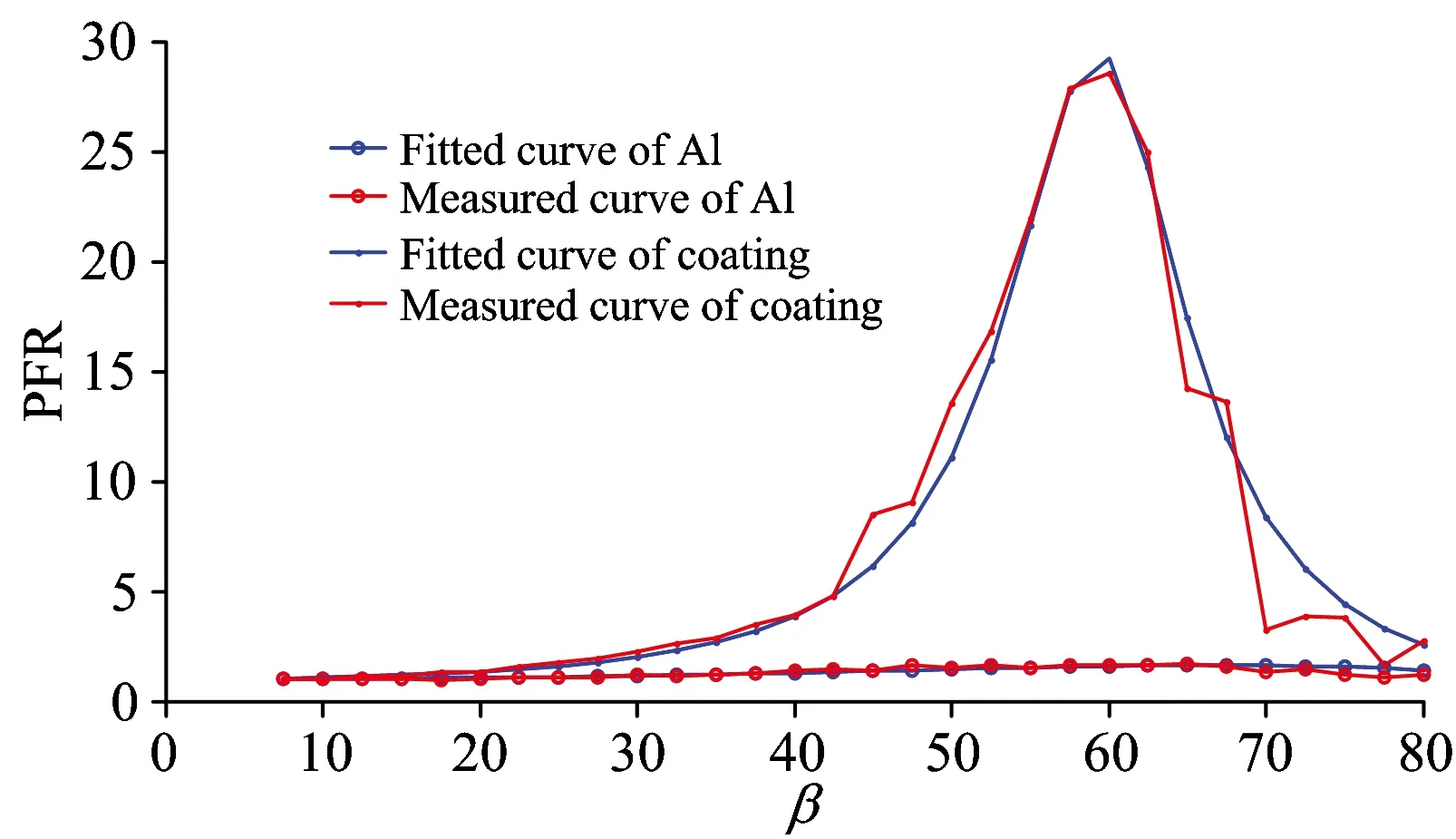
图4 合金铝和涂料在不同探测方向的偏振 菲涅尔系数比PFR曲线拟合结果

为了验证不同材料的偏振菲涅尔系数比PFR分布曲线，并且对比不同材料的PFR分布曲线的异同。实验对合金铝和涂料两种材料进行了测量。图4为对合金铝和涂料的偏振菲涅尔系数比PFR随着β角变化的分布测量结果，根据参数拟合曲线的系数，合金铝的光学参数折射率和消光系数为n=0.622 1，k=2.367 4，涂料的光学参数为n=1.602 8，k=0.461 3。从图4中曲线可以看出，涂料和合金铝的曲线在β角小于20°时的区分度并不是很高，但是当β角大于20°，涂料和合金铝的曲线分布明显不同，这个不同在当β角在60°附近的涂料曲线有峰值，而铝的PFR曲线相对比较平缓，本质上就是由材料的光学常数决定的。通常，消光系数越小，这个峰值就越明显，而当消光系数为0时，峰值将会达到无穷，这一特点本身就可以作为区分金属和非金属材料的重要特性。需要说明的是，这里的测得的铝的消光系数不到3，与文献[12]中的纯铝的消光系数为6左右有出入，原因在于本实验中采用的为铝合金材料，而非纯的金属铝，通过椭圆偏振测量法测量了该铝合金材料的光学常数，其消光系数约为2.43，与本文方法测量所得在误差允许的范惜内是一致的。

5 结 论

从仿真和实际测量实验的结果可以看出，不同的材料有不同的偏振菲涅尔系数比PFR，并且PFR在入射角或者出射角不同的情况下也不同，因此利用PFR随着角度的分布来辨别目标的效果十分显著，由于PFR的分布是和目标材料的光学常数有关，PFR分布的不同归根结底是目标材料的不同，所以利用探测目标的多个角度的PFR数据能够快速准确的区分出不同的材料，这一特性在目标识别，特别是假目标的辨识、伪装材料的辨别等领域有着十分广阔的应用的前景。

[1] Martin Laurenzis, Jean Michel Poyet, Yves Lutz, et al. Proceedings of SPIE—The International Society for Optical Engineering, 2012, 8542: 854203.

[2] Lemaster D A, Mahamat A H, Ratliff B M, et al. SPIE Optical Engineering and Applications. International Society for Optics and Photonics, 2013. 307.

[3] LI Quan, LIU Ze-jin, SHU Bo-hong, et al(黎 全, 刘泽金, 舒柏宏, 等). High Power Laser and Particle Beams(强激光与粒子束), 2005, 17(3): 351.

[4] ZHANG Xu-guo, JIANG Yue-song, LU Xiao-mei, et al(张绪国, 江月松, 路小梅, 等). Journal of Applied Optics(应用光学), 2008, 29(4): 580.

[5] WEN Dong-hai, JIANG Yue-song, HUA Hou-qiang, et al(闻东海, 江月松, 华厚强, 等). Infrared and Laser Engineering(红外与激光工程), 2014, 43(4): 1130.

[6] Priest R G, Meier S R. Optical Engineering, 2002, 41(5): 988.

[7] WANG Xia, ZOU Xiao-feng, JIN Wei-qi(王 霞, 邹晓风, 金伟其). Transactions of Beijing Institute of Technology(北京理工大学学报), 2011, 31(11): 1327.

[8] Conant J A, Iannarilli Jr F J. International Symposium on Optical Science and Technology. International Society for Optics and Photonics, 2002. 206.

[9] Fetrow M P, Wellems D, Sposato S H, et al. International Symposium on Optical Science and Technology. International Society for Optics and Photonics, 2002. 149.

[10] Wolff L B. IEEE Transactions on, Pattern Analysis and Machine Intelligence, 1990, 12(11): 1059.

[11] Melissa A S，Milo W H. SPIE Optical Engineering and Applications. International Society for Optics and Photonics, 2013. 379.

[12] Wakaki M, Kudo K, Shibuya T, et al. Physical Properties and Data of Optical Materials(光学材料手册). Translation by ZHOU Hai-xian, CHENG Yun-fang(周海宪, 程云芳, 译). Beijing: Chemical Industry Press(北京： 化学工业出版社), 2010.

(Received Apr. 10, 2015; accepted Aug. 18, 2015)

A Target Discrimination Method Based on the Active Polarization Imaging with the Distribution of Polarization Fresnel Ratio

GENG Li-xiang1, 2, CHEN Qian1, 2, QIAN Wei-xian1，GU Guo-hua1，PAN Jia-hui1

1. School of Electronic Engineering and Optoelectronic Technology, Nanjing University of Science and Technology, Nanjing 210094, China 2. Jiangsu Key of Spectral Imaging & Intelligent Sense, Nanjing University of Science and Technology, Nanjing 210094, China

As the polarization characteristics are the physical property determined by the material itself, its corresponding polarization image contains abundant target’s information. Using polarization information to identify the target is always a hot research topic in the field of the target detection. Active polarization imaging has more advantages compared with passive polarization imaging because of its high signal-to-noise ratio and good controllability. In this paper, based on the detailed analysis of the theory of the distribution of polarization Fresnel reflectance ratio, a kind of active polarization imaging method is proposed with detecting the polarization Fresnel ratio of the surface of the object. The proposed method adopts two kind of polarization light with orthogonal polarization direction at the light emission part to exposure to the target scenario alternately. Then two cameras side-by-side at the detecting part respectively equipped with two orthogonal polarization direction filters to capture the polarization images. Meanwhile, the detectors are placed in different detecting direction to acquire the polarization imaging with active polarization light source illuminating. Finally, with transmitting the data to the calculating center, optical constants can be recovered from the polarization data by the optimization fitting technique. Because the materials of target’s surface are different, the corresponding optical constants are different. Then the purpose of discriminating the targets with different materials is achieved. The simulated and actual measured experiments are explored to verify the effectiveness of the proposed method. Simulation experiment shows it is not only scientific but also more convenient and effective in that the proposed method can distinguish the different materials using the calculated optical constants. The actual measured data further shows that the method is able to do better in recover optical constants of targets, especially in the distinction between metal and dielectric materials. Furthermore, the system has great application prospect in the field of target detection and camouflage recognition with its simple structure and practicability.

Active polarization detection; Polarization fresnel ratio; Bidirectional reflectance distribution function; Polarization imagine

2015-04-10，

2015-08-18

国家自然科学基金项目(61101199)，新世纪优秀人才支持计划基金项目(NCET-12-0630)，江苏省“六大人才高峰”计划基金项目(2012-DZXX-037)，江苏省仪器平台分析测试课题(BZ201309)资助

耿利祥，1986年生，南京理工大学电子工程与光电技术学院博士研究生 e-mail： 1376594359@qq.com

TH744.2

A

10.3964/j.issn.1000-0593(2016)06-1916-05