宽谱段共光轴线色散成像光谱仪三棱镜分光系统设计

刘 兵，刘 英，张晓龙，李 灿，王 健，李 淳*，孙 强

1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033 2.中国科学院大学，北京 100049 3.青岛滨海学院，山东 青岛 266555

宽谱段共光轴线色散成像光谱仪三棱镜分光系统设计

刘 兵1, 2，刘 英1，张晓龙3，李 灿1，王 健1，李 淳1*，孙 强1

1.中国科学院长春光学精密机械与物理研究所，吉林 长春 130033 2.中国科学院大学，北京 100049 3.青岛滨海学院，山东 青岛 266555

针对棱镜型成像光谱仪结构复杂、具有严重的色散不均匀性，进行了共光轴线色散棱镜式宽谱段成像光谱仪研究。利用棱镜的色散公式建立了对称型三棱镜组合分光结构的数学模型，获得了满足直视结构的棱镜组合，并在此基础上分析影响棱镜组色散线性因素：棱镜材料的折射率和色散率对棱镜组线色散影响比较大，入射角度对其影响比较小，并提出改善色散线性的方法，获得了满足线色散要求的棱镜组合的折射率条件，从而为共光轴结构的线色散棱镜式成像光谱仪初始结构的选择提供了重要理论依据。在工作波段为400～1 000 nm、中心波长偏向角为0°、最大色散角为0.6°、光谱仪系统数值孔径NA为0.18、光谱分辨率为5 nm条件下，实现共光轴三棱镜分光系统的线色散设计，最后利用ZEMAX进行了模拟分析表明，理论计算结果与实际仿真结果基本相符。

三棱镜组合； 线色散； 共光轴； 直视结构； 宽谱段； 成像光谱仪

引 言

成像光谱仪由于能够同时获得目标的图像信息和光谱信息，而广泛应用在航空、航天器等观测系统中[1]。按照工作原理的不同，成像光谱仪分为色散型、滤波片型、干涉型和计算层析型[2-3]。目前应用最广泛的是色散型成像光谱仪。色散型光谱仪由于色散元件的不同，可以归纳为棱镜分光、光栅分光和棱镜-光栅组合分光[4-6]。利用光栅作为分光元件，存在很大的局限性。例如光栅系统在宽谱段分光时，存在谱线叠加问题； 光栅是衍射分光，故实际能量利用率只能达到总能量的60%～70%[7]； 由于制作工艺的限制，杂散光比较多、加工难度相对比较大等问题。应用棱镜作为分光元件便可以很好的解决此类问题，像意大利航天局的PRISMA，欧空局的CHRIS，上海技物所的OASIS，海洋水色成像仪[8-9]都成功应用棱镜实现了宽谱段无重叠线性分光。但是只有三棱镜组合才能实现共轴光路(中心波长出射光束与入射光束位移为0)设计，为仪器的装调带来极大的方便，同时也能实现色散线性。但是目前尚未有具体的针对于三棱镜组的相关理论计算方法。

针对于此，本文从三棱镜组的特性出发，理论计算棱镜组线色散条件。对直视型对称结构棱镜组进行分析[12]，提出共轴光路的条件。在光束小角度入射的前提下，根据选定材料，分析计算棱镜组的结构，再通过迭代算法进行优化设计，最终设计了共轴性好、色散线性化程度高的直视型对称结构棱镜组，结合数据进行分析，探究棱镜组实现色散线性的方法。最后利用ZEMAX软件验证所设计的有效性和可靠性。

1 三棱镜系统参数确定

成像光谱仪系统由前置望远物镜和光谱成像系统组成[12]，前置望远物镜将目标成像在狭缝上，再经过光谱成像系统准直、分光、成像在探测器CCD上。

设定准直系统和成像系统的焦距为100 mm(对于光谱仪系统为了保证设计的方便性，一般做成放大倍率为-1的成像系统)，光谱成像系统的数值孔径NA为0.18(为了获取足够的目标能量，前置望远物镜的F/#一般取2.8，按公式NA≈1/(2F#)计算得到，以保证光谱系统与前置望远物镜光瞳相匹配)。鉴于可见/近红外波段(400～1 000 nm)是地面目标的主要反射谱段，同时也是许多卫星遥感器扫描成像的常用波段[13]，因此，文中选择系统的工作波段400～1 000 nm。为实现光谱分辨率为5 nm，同时保证线色散以及仪器的结构紧凑，选择色散角为0.6°。对于共光轴直视型结构棱镜组，中心波长偏向角为0°, 出射光束与入射光束的光轴偏移量为0 mm，如图1所示，其中λ0为700 nm，λ1为400 nm，λ2为1 000 nm。综上分析，表1给出了共光轴直视型成像光谱仪系统的设计参数。

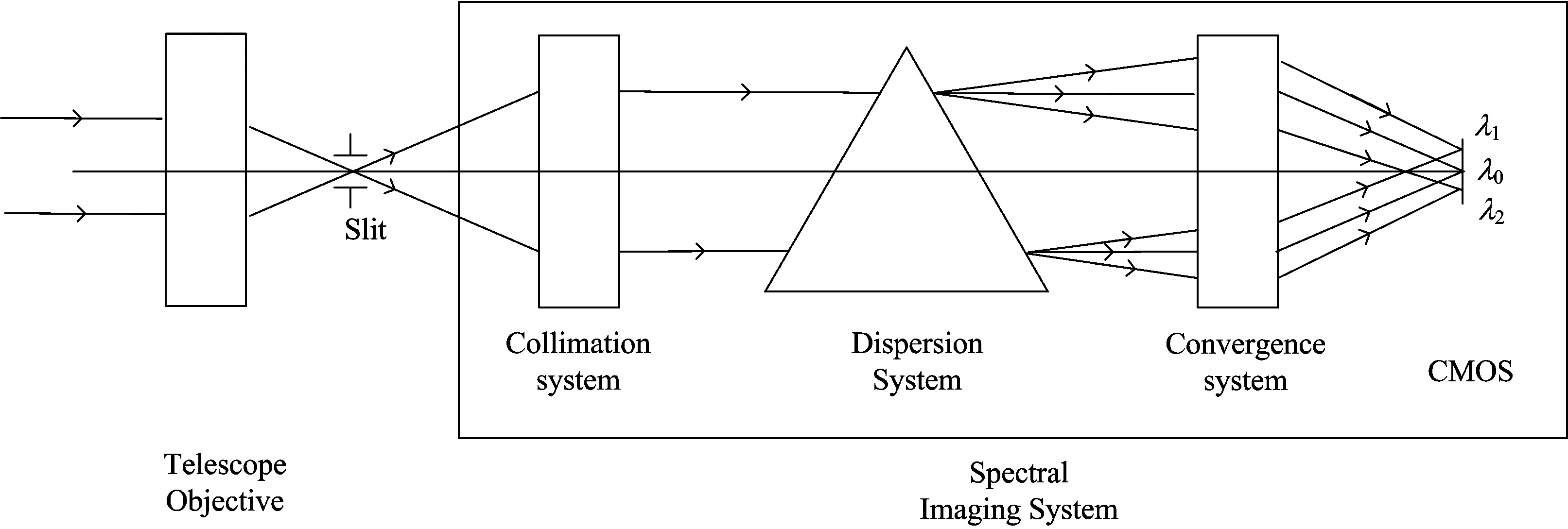
图1 成像光谱仪系统

表1 共光轴直视型棱镜组设计参数

2 棱镜组线色散计算以及共光轴直视型棱镜组结构计算

本文从棱镜组的特性出发，建立与光束角度、棱镜组顶角、棱镜折射率以及棱镜材料相关的线色散表达式。理论计算直视型棱镜组共光轴条件，在此前提下，建立三棱镜组的结构模型，并且利用迭代算法进行优化，最终得到满足线色散的共光轴直视型对称结构棱镜组。

2.1 三棱镜系统线色散表达式推导

出射光束相对入射光束的夹角为偏向角δ，则知

(1)

通过棱镜组传输的光束中长波偏向角与短波偏向角之差为色散角Δ，则知

(2)

将式(1)带入式(2)，求得棱镜组的色散角。

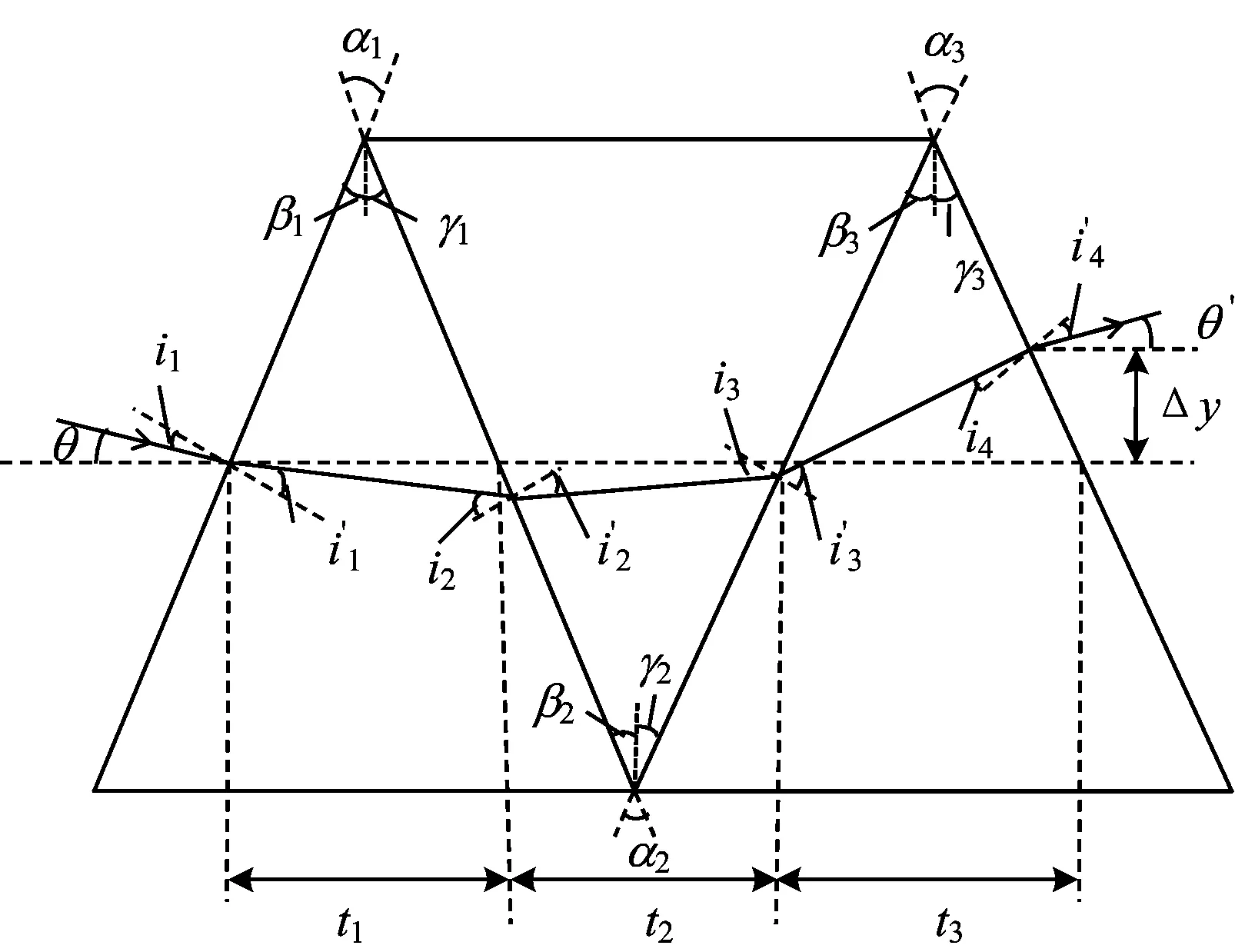
图2 三棱镜分光系统示意图

(3)

(4)

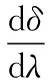
(5)

2.2 直视型棱镜组共光轴条件推导

对于直视型对称结构的棱镜组，当中心波长光束在内层棱镜中处于最小偏向角的状态时，光路对称，此时出射光束与入射光束的偏移量为0，出射光束的宽度与入射光束一致。这样可以在保证像方数值孔径不变的前提下实现共轴光路设计。故选择直视型对称结构棱镜组作为初始结构，系统自由变量简化为4个(α1，α2，n1，n2)。其中入射角i1=-β1，顶角α2=-2γ1，顶角α3=γ1-β1，棱镜组的等效顶α组=-2β1=2i1，n1=n3。

根据子午面内折射定律，易推得

(6)

当β1是小角度时, 且γ1≫β1时，即α2≈2α1=2α3时

(7)

当β1，γ1均是小角度，且γ1≈β1时，即α2≈α1=α3时

(8)

根据式(7)和式(8)即知小角度入射情况下：两种特殊结构下，α2≈2α1=2α3和α2≈α1=α3，棱镜材料的关系。

2.3 棱镜顶角确定

在给定棱镜组结构时，根据式(1)和式(2)利用实际光线追迹的方法，可以准确的求出棱镜组的色散角和中心光束的偏向角。但是无法通过反向光线追迹求得棱镜组的结构。为此，先利用小角度入射角时，偏向角和色散角的近似公式求解顶角初始值，再利用MATLAB软件优化，得到精确顶角数值解。当入射角i1是小角度时，单个棱镜的偏离角δ和色散角Δ有经验式(9)和式(10)。其中n长为长波时棱镜材料的折射率，n短为短波时棱镜材料的折射率。

δ=(n-1)α+lα3

(9)

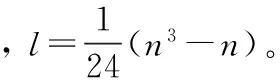
Δ=(n长-n短)α+pα3

(10)

对于对称型三棱镜，外层两个棱镜参数一致。假定三棱镜是独立在空气中，并没有胶合，根据三棱镜需必须满足直视条件，建立式(11)； 系统所需色散角建立式(12)。

(11)

Δ组=2Δ1+Δ2=0.6

(12)

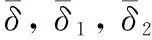
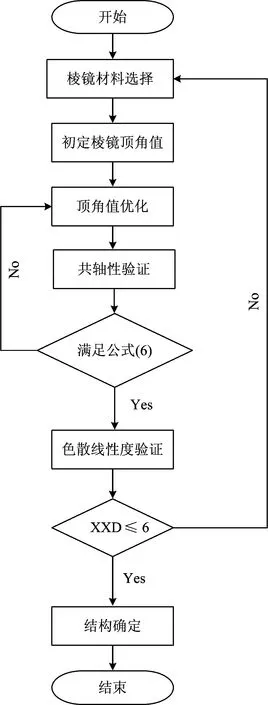
图3 直视型对称结构棱镜组设计流程

根据实际光线追迹的偏向角、色散角的式(1)和式(2)，利用迭代算法优化，得到选定材料下，满足条件棱镜顶角值。

2.4 色散线性度算法实现过程

实现共光轴直视型对称结构三棱镜组的设计过程中需要利用迭代算法计算，下面给出算法的具体实现过程，图3为算法实现的流程图。

(1)棱镜组材料确定。根据需求棱镜组顶角的区间值，利用式(6)，初步计算棱镜材料中心波长折射率范围值，在此区间内选择材料。

(2)棱镜组顶角值初定。利用式(11)和式(12)，求得棱镜组的顶角值。由于偏向角和色散角公式是小角度入射的经验公式，并且在计算中，假定棱镜是各自独立的，并没有胶合，所以顶角值要进行优化。

(3)顶角值优化。根据实际光线追迹的偏向角、色散角的式(1)和式(2)，利用迭代算法优化，得到选定材料下，满足式(11)和式(12)棱镜顶角值。

(4)共轴型验证。棱镜组顶角值的计算过程中，满足条件的顶角值解并不唯一，这时利用共光轴直视型式(6)对顶角进行筛选。最终得到满足要求的棱镜组结构。

(5)色散线性度验证。棱镜色散非线性，会导致光谱的采样间隔不一致，给仪器的光谱配准带来困难，并且会影响光谱仪器的灵敏性和准确度。所以设计时，尽可能实现色散线性化。XXD越接近1时，线性化程度越好。但是对于共光轴直视型对称结构的棱镜组, 由于共光轴条件限制了棱镜组的入射角、直视型条件限制了棱镜组顶角，故XXD≤6，就可以认定色散线性良好。若不满足条件，重新选择材料进行运算。

3 结构优化结果以及仿真实验

3.1 数据分析

表2 共光轴直视型对称结构三棱镜数据表格

根据表2中数据，结合图4(c)可知：外层材料是CAF2，内层材料是FK5的两组数据对比可知，利用三棱镜组完全可以实现线性色散。但是在共光轴直视型棱镜组的限制下，棱镜组的色散非线性程度会增大。在此前提下实现棱镜组线性色散的最佳选择为外层材料是CAF2，内层材料是FK5。棱镜组顶角分别为(47.7°，-82.94°，47.7°)。

图4中曲线与坐标轴所围面积就是色散角。根据图4可知，要在固定色散角下实现色散线性，只要压制短波处的色散率或是提高长波处的色散率即可。

结合表2中数据和图4(a)进行综合分析，在给定一种棱镜材料前提下，可知棱镜组内层材料的折射率越接近外层材料，线性度越好。

结合表2中数据和图4(b)中数据进行分析，在棱镜组内层材料折射率近似情况下，选择材料色散能力在短波范围内越小(阿贝数越大)，即与外层材料的色散值越接近，线性度越好。

直视型对称结构棱镜组线性色散除与材料的选择有关，还与入射角度和棱镜顶角有关。下面探讨入射角i1的改变对棱镜组色散线性的影响。选择棱镜组合为外层材料为CAF2，内层材料为SF6。数据见表3。

对表3中数据进行分析，在给定棱镜材料的前提下，随着入射角i1的增大，即组合棱镜的顶角α组的增大，棱镜组的色散非线性化程度增大，但是变化的幅度不大，同时色散角增加。这也表明当系统要求大的色散角时，系统的色散线性会变差。

结合上述分析，得出共光轴直视型对称结构棱镜组的色散线性程度与材料的选择关系密切、与顶角的变化关系不大。对于小色散系统，在选择CAF2为外层材料前提下，选择棱镜组内层材料的折射率越低，色散越线性； 在内层材料折射率相近的时候，选择材料的阿贝数越大，色散越线性。

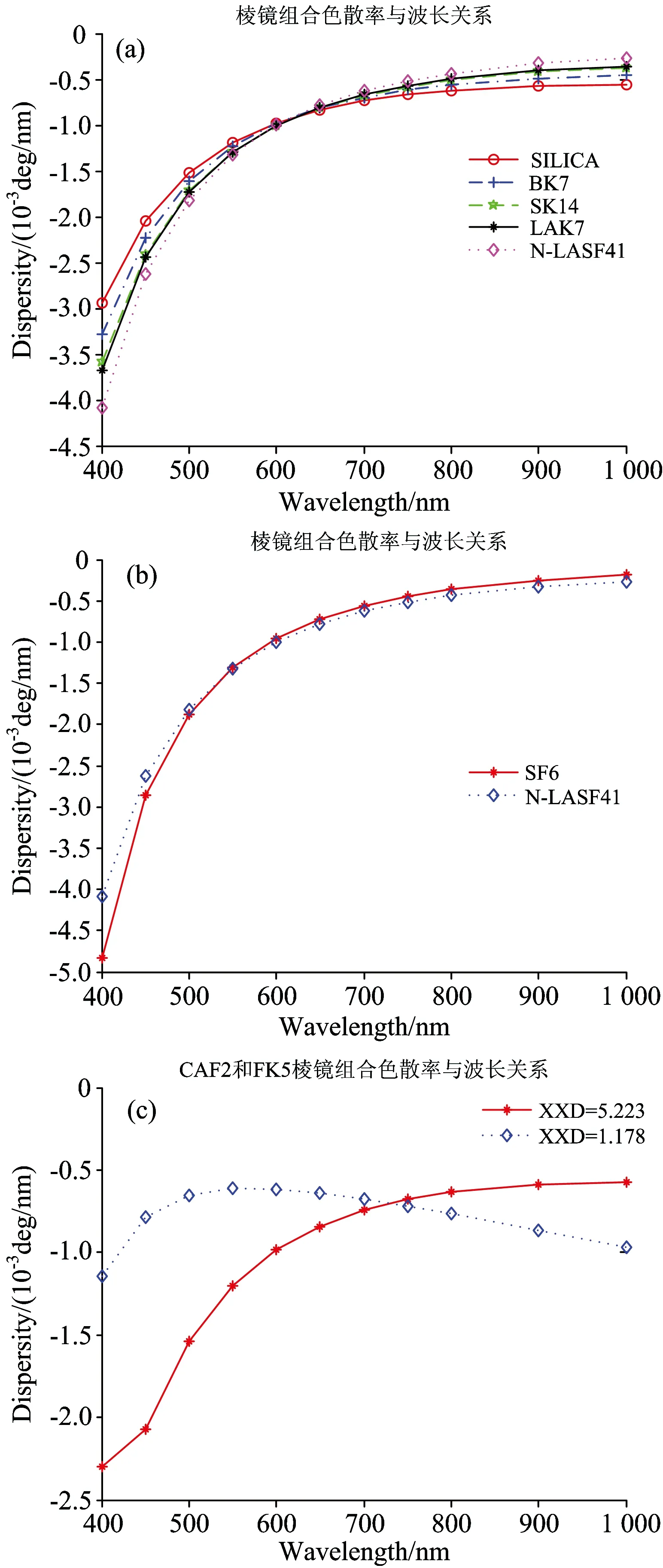
图4 棱镜组色散率

表3 共光轴直视结构下入射角度色散率的影响

3.2 ZEMAX仿真实验

对于理论建模，利用ZEMAX进行仿真模拟，以证明模型的可靠性。模型参数设置与理论建模一致，波长范围400～1 000 nm，物方孔径NA为0.18，准直系统和成像系统均采用理想透镜，透镜焦距100 mm。根据表1，选择线性度最好的棱镜组：内层材料选择FK5，外层材料选择CAF2。仿真模拟图见图5所示。

图5 验证分析

图5(a)为共光轴直视型对称结构三棱镜光路图。从图5(b)中可以得知，在像面上色散距离为1 000 μm左右，即棱镜的色散角为0.6°。色散线性程度与理论计算基本一致。

4 结 论

由于各类型小型飞机尤其是无人机的发展，成像光谱仪的小型化和轻型化越来越受到重视。利用棱镜作为分光元件可以实现宽谱段成像光谱仪结构紧凑、装调快捷、使用方便等要求，但是棱镜型成像光谱仪结构复杂、具有严重的色散不均匀性，为此，本文对共光轴线色散棱镜式分光系统展开研究，并提出了直视型对称结构棱镜组的初始结构计算方法，给出了直视型对称结构棱镜组的共光轴条件，利用迭代算法优化，获得棱镜组结构参数。在两种特殊顶角需求下，建立了棱镜材料中心波长折射率关系式。提出了实现棱镜组线性色散的方法，即选择内层材料与外层材料的折射率和阿贝数均接近容易实现棱镜组的线性色散。为棱镜分光系统实现线色散研究提供一种求解、优化思路。

[1] ZHANG Xiao-long, LIU Ying, SUN Qiang(张晓龙，刘 英，孙 强).Acta Optica Sinica(光学学报), 2012，32(11)：1122005.

[2] ZHENG Yu-quan, WANG Hui, WANG Yi-fan(郑玉权，王 慧，王一凡).Optics and Precision Engineering(光学 精密工程), 2009, 17(11): 2629.

[3] YANG Jin, TANG Yu-guo, Bayanheshig(杨 晋，唐玉国，巴音贺希格).Acta Optica Sinica(光学学报)，2012, 32(11)：1130003.

[4] Braam T, Okkonen J T, Aikio M, et al.SPIE, 1993, 1937: 142.

[5] YANG Zeng-peng, TANG Yu-guo, Bayanheshig(杨增鹏，唐玉国，巴音贺希格).Acta Optica Sinica(光学学报)，2014, 34(9): 0911003.

[6] WU Cong-jun, YAN Chang-xiang(吴从均，颜昌翔).Journal of Applied Optics(应用光学)，2012, 33(1)：37.

[7] WU Cong-jun, YAN Chang-xiang，LIU Wei(吴从均，颜昌翔, 刘 伟).Acta Optica Sinica(光学学报)，2013, 33(12)：1222001.

[8] Puschell J J.SPIE, 2000, 4041(121): 121.

[9] Cutter M A, Lobb D R.SPIE, 1999, 3753: 180.

[10] WANG Yi-qun, MIAO Chun-an, YAN Chang-xiang(汪逸群，苗春安，颜昌翔).Chinese Journal of Optics and Applied Optics(中国光学与应用光学), 2009, 2(4)：304.

[11] Blechinger F.Harnisch B, Kunkel B.SPIE, 1995, 2080: 165.

[12] PEI Lin-lin, HUANG Min, LÜ Qun-bo(裴琳琳，黄 敏，吕群波).Acta Optica Sinica(光学学报)，2013, 33(1): 0122003.

[13] CHEN Shi-ping(陈世平).Space Camera Design and Test(空间相机设计与试验).Beijing: Aerospace Press(北京：宇航出版社)，2003.21.

(Received Dec.26, 2014; accepted Mar.9, 2015)

*Corresponding author

Study on Coaxial Linear Dispersion Triplet Prisms of Wide Spectral Imaging Spectrometer

LIU Bing1, 2，LIU Ying1，ZHANG Xiao-long3，LI Can1，WANG Jian1，LI Chun1*，SUN Qiang1

1.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033, 2.University of Chinese Academy of Sciences, Beijing 100049, 3.Qingdao Binhai University, Qingdao 266555, China

To overcome the difficulties of complex structure and serious nonlinear dispersion in prismatic imaging spectrometer the coaxial linear dispersion prismatic imaging spectrometer is investigated in this paper.A mathematical model of symmetric triple prisms’ beam splitting system is constructed with prism's dispersion equation, and the prisms assemble of direct view is obtained.Then the factors affecting dispersion linearity are analyzed.The refractive index and dispersion rate of prism material impact dispersion linearity most while the influence of incident angle is very small.The way to improve dispersion linearity is given and the refractive index condition meeting the requirement of dispersion linearity of prisms is obtained.It provides important basis to select the initial structure for coaxial linear dispersion triplet prisms of imaging spectrometer.On condition that the working band of 400～1 000 nm, center wavelength deviation angle 0°, the maximum dispersion angle 0.6°, object numerical aperture 0.15 and spectral resolution 5 nm, we succeed in designing coaxial linear dispersion triplet prisms.Digital simulation with ZEMAX is performed, and the results are in accordance with theoretical analysis.

Triple prisms; Dispersion equation; Coaxial; Direct view; Wide spectral bands; Imaging spectrometer

2014-12-26，

2015-03-09

国家自然科学基金重点项目(61137001)，国家重大科学仪器设备开发专项(2013YQ140517)资助

刘 兵，女，1986年生，中国科学院长春光学精密机械与物理研究所博士研究生 e-mail：liu32060209@163.com *通讯联系人 e-mail：liuy613@163.com

TH744.1

A

10.3964/j.issn.1000-0593(2016)05-1543-06