模考把关题命制要挖掘教材资源——以一道中考模考题为例

☉江苏省苏州市张家港市后塍学校　李文俊



模考把关题命制要挖掘教材资源
——以一道中考模考题为例

☉江苏省苏州市张家港市后塍学校李文俊

一、写在前面

在文1中，周礼芳老师针对江苏省海安县2015年中考调研卷的把关题的解题思路、命题立意和教学导向进行了阐释，读后既为命题组的匠心独运、原创精神而感动，也从周老师的解读中深入了解到该题的教学功能，受益其中.笔者对该地区的2016年中考调研卷保持着关注和研究，本文就选取该地区2016年中考调研卷把关题，也给出思路突破和命题立意的阐释，供研讨.

二、模考把关题及思路突破

模考题（2016年4月江苏省海安县中考调研考试，第28题，13分）如图1，在平面直角坐标系xOy中，点A的坐标是（0，-2），在x轴上任取一点M，连接AM，作线段AM的垂直平分线l1，过点M作x轴的垂线l2，记l1、l2的交点为P.在x轴上多次改变点M的位置，得到相应的点P，会发现这些点P竟然在一条抛物线L上！记点P（x，y），连接AP.

图1

（1）求出y关于x的函数解析式；

①求点M的坐标；

②设点N在直线l2上，点Q在抛物线L上，当PN=1，且AQ、NQ之和最小时，求点Q的坐标.

思路突破：（1）如图2，连接AP，作PB⊥y轴于B，由l1垂直平分AM得PA=PM=-y.

图2

在Rt△ABP中，BP=OM=x，BA=PM-OA=-2-y，根据勾股定理，得（-2-y）2+x2=y2，整理得能带来怎样的信息，如图2，容易转化为∠PAB的正切函数值为

（2）关键是解读“锐角∠APM的正切函数值为即△ABP是一个“3，4，5”式的特殊直角三角形，进一步可设AB=3a，BP=4a，从而得到P的坐标（4a，-2-3a），于是代入抛物线解析式中，可获得点P的坐标（4，-5），相应的点M的坐标为（4，0）.此时还要注意另一种情况，即当点P在第三象限时，由对称性同理可得点M的坐标为（-4，0）.综上可知，①中点M的坐标为（4，0）、（-4，0）.

②如图3，当点M为（4，0）时，点P的坐标为（4，-5）.由点N在直线l2上且PN=1，可得点N的坐标为N1（4，-4）或N2（4，-6）.当点N在点P上方即为N1（4，-4）时，连接AN1交抛物线于点Q1.

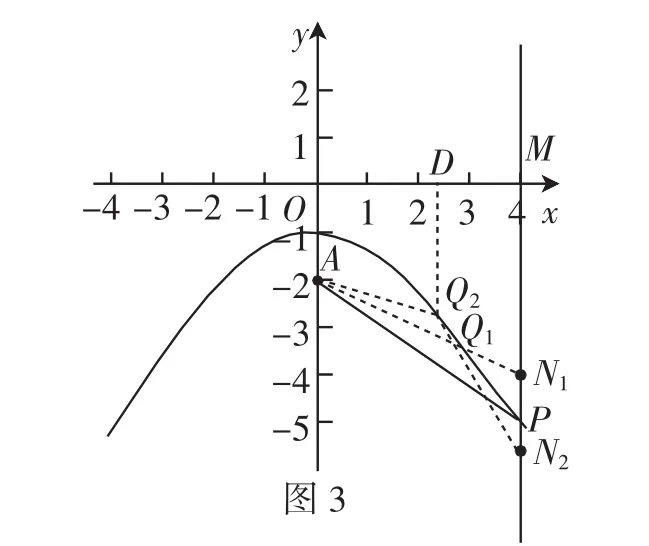
图3

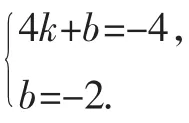
根据对称性，当点M为（-4，0）时，点P的坐标为（-4，-5）.

附：从我们获得的评分标准中发现，有如下一段“评分建议”：作为全卷最后一题，命题组有如下意图，供评卷组参考.比如（2）①漏一解，只宜扣1分，并不是求出一个点M的坐标就得2分；（2）②中，如果整体上N点漏掉一解，相应的点Q的两解都正确，则扣2分为宜；如果整体上N点漏掉一解，对于点Q只考虑了一解，则整体上扣3分为宜；其余情况由阅卷组长集中意见、统一尺度评分，总之给分要有据可依，扣分要合情合理.

三、解后反思

1.问题主要障碍在哪儿？

从上面的求解来看，问题的主要障碍在构造相对精准的草图分析，并在草图的基础上标注恰当的字母，特别是根据所给的条件“锐角∠APM的正切函数值为能否发现并利用“3，4，5”式的直角三角形进行问题演算；此外，本题求解中还容易漏解，所以基于轴对称性质的分类讨论也是值得重视的.

2.解后能收获怎样的经验？

本题起点是探究出抛物线的解析式，进一步重视特殊图形的发现、构思与利用.一般来说，对于中考综合题的突破，常常需要在无图题前构造图形，在一般图形中发现特殊图形、模式图形、经典模式，这里发现、捕捉、构造都考验着考生的解题能力和转化的智慧.

四、进一步的思考

1.命制把关题要重视挖掘教材资源

当前不少地区的中考模考命题（包括有些期中、期末统考卷命题），一个“流行”的做法是到各地中考试卷中“直接拿来”，这种简单复制粘贴的“拿来主义”，助长了题海战术与机械应试，给教学带来不良影响，而上文中的这道把关题直接取材于教材上的内容，重视挖掘教材资源，对一些奉行“拿来主义”的命题方式是一次很好的纠偏，值得点赞.

2.问题改编、拓展设计的可能角度

从该地区连续两年聚焦同一个教材资源并从不同角度设计把关题来看，问题的设问多样化，令人佩服.比如经过文1的介绍，上一年度对该题的考查，主要是尺规作图，猜想、探索、验证函数解析式，并强化出一个等边三角形后深入探究；而这一年度则是在题干中明确告知这是一个抛物线，第一问先求解析式，然后添加强化条件得出一个“3，4，5”式的直角三角形引导探讨，并结合对称性分类讨论.显示了这一问题背景或平台的宽广，可以承载不同命题方式或设问的众多角度.

3.对教学的导向是重视“用教材教”

由上述解法及评析可知，这道把关题的一个重要的教学导向是引导广大备考师生重视“用教材教”（钟启泉语）.具体来说，坚持“以本为本”，教学不能离开课本，不能以中考题代替教材，不能以习题单式的学案代替教材；从“教教材”走向“用教材教”，以解题教学为例，不能仅仅止步于教一道题，而要善于发挥教材习题或活动材料的解题教学的价值，通过对问题进行必要的改编、生长或拓展，追求“教一题、会一类、通一片”的教学效果.

参考文献：

1.周礼芳.重视教材“活动”材料，追求变式教学效率——以一道中考模考卷压轴题为例［J］.中学数学（下），2015（6）.

2.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.

3.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.Z