基于火箭弹旋转运动的主子惯导在线标定方案研究

王志伟，石志勇，全振中

军械工程学院，石家庄　050003）



基于火箭弹旋转运动的主子惯导在线标定方案研究

王志伟，石志勇，全振中

军械工程学院，石家庄050003）

摘要：针对火箭炮在不能进行线运动，只能进行两自由度的角运动，以及需要标定参数多，模型维数大导致标定实时性差炮制导化改造为背景，首先利用旋转调制的原理建立了误差模型，将惯性器件的零偏误差分离，并且理论分析了旋转调制对惯性器件刻度系数误差标定的影响，分析结果表明，旋转运动对刻度系数误差的可观测性影响很大。但是，由于单独的横滚运动不能激励全部6个刻度系数误差，所以最后设计了新的火箭弹机动方案，以及滤波算法使全部刻度系数误差均可观测，并且结果表明除x轴陀螺刻度系数误差外，其余参数均能较快地收敛，与传统的方法相比，标定的实时性和精度都有了较大提高，充分体现了弹丸横滚运动对火箭炮射前标定的重要性。

关键词：火箭弹，旋转运动，主子惯导，在线标定

0　引言

由于成本的限制，火箭弹的弹载惯导只能采用低成本、精度较低的惯性器件，在射击前必须对其进行误差标定。在国内，关于弹载惯性组合标定的研究较多，许多方法需要将惯组从弹中取出，在简易台架上通过适当的转位进行标定［1-2］，还有一些学者也提出了一些不拆卸的标定方法，如利用导弹发射车从库房到发射阵地的姿态变化和导弹竖立过程中的各姿态进行标定［3-4］等。但是这些方法没有充分利用武器平台的高精度定位定向系统的输出信息，需要进行复杂的操作。并且火箭炮在射前标定阶段不能进行线运动，只能进行两自由度的角运动，参数可观测度低，不能适应现代战争的需求。文献［5］通过理论分析，得出在火箭炮射前准备阶段加入横滚运动可以使大部分误差参数的可观测度得到提升，但是21维的误差模型导致了大运算量，从而影响了标定的实时性。

1　旋转火箭弹误差传播方程

本文的研究背景是火箭炮的制导化改造，而该型火箭炮的主惯导安装在摇架上，子惯导安装在火箭弹体上，所以在对主子惯导系统建立旋转条件下的误差模型前，设定n为导航坐标系；i为惯性坐标系；m为主惯导坐标系；s为子惯导坐标系。另外，由于在初始状态时，摇架和弹体平行，故主惯导（m）和子惯导（s）的坐标系重合。

主惯导到惯性系的转换矩阵为。

子惯导绕y轴转动时到主惯导的旋转矩阵为。

ωs为子惯导相对主惯导转动的角速度。

设φ为姿态误差，δV为速度误差，忽略陀螺和加速度计的安装误差及刻度因数误差，忽略经纬度误差的影响，弹丸导旋转状态下的主子惯导系统误差方程为：

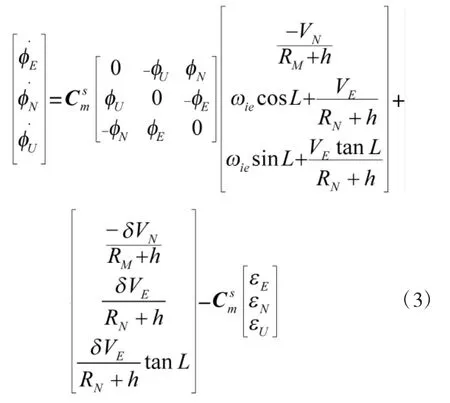
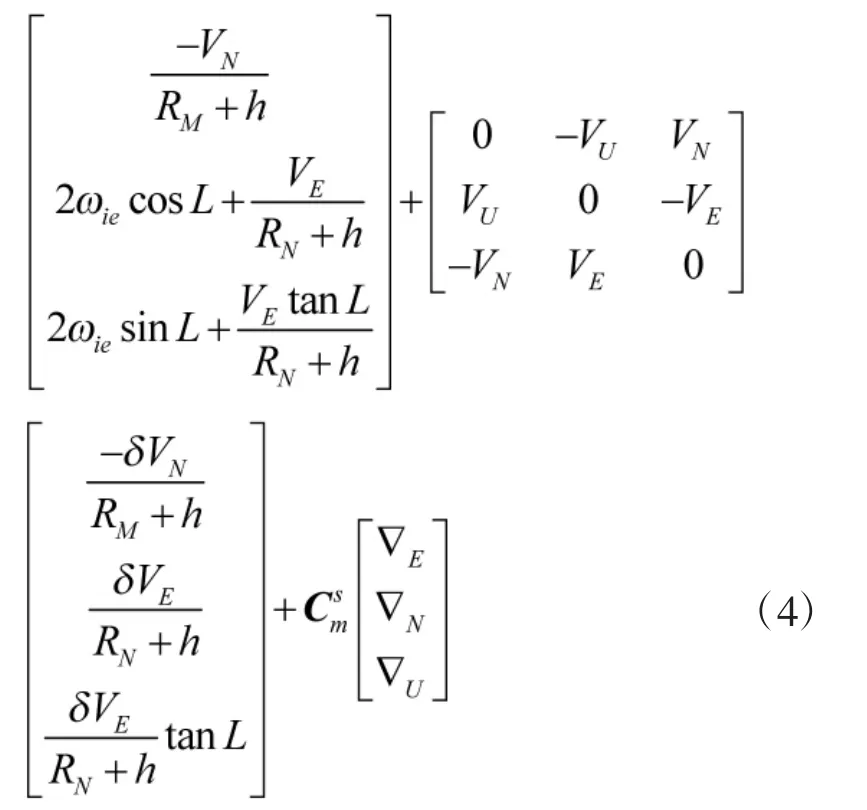
其中，h为高度，L为纬度，RMRN为子午圈和卯酉圈曲率半径，VE=VN=VU=0。

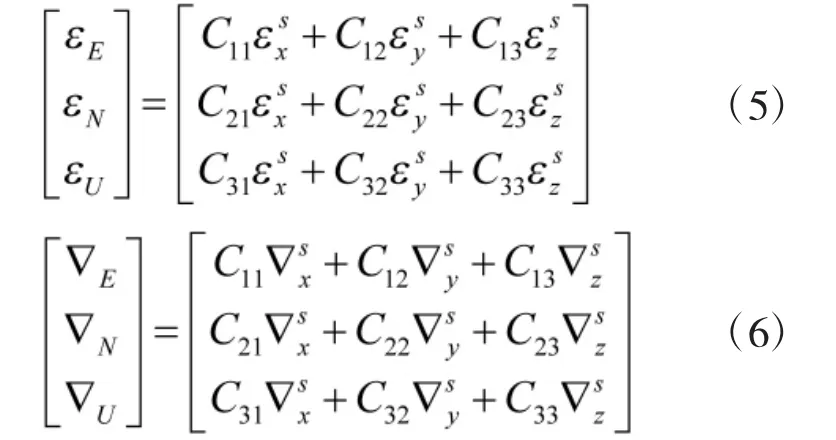
εis（i=x，y，z）为陀螺常值漂移；△is（i=x，y，z）为加计零偏。

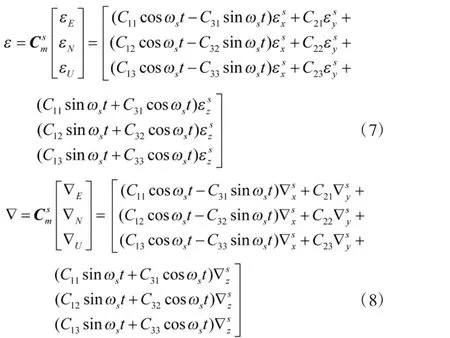
其中，ε、△为旋转条件下加计和陀螺零偏造成的等效零偏，由式（7）、式（8）可以看出，ε、△在3个方向上均得到了调制，使得等效零偏ε和△非常小。

2　旋转条件下的误差分析

由于在旋转条件下，惯性器件的零偏被调制，但是加速度计和陀螺的刻度系数误差得不到有效调制，所以为了提高导航精度，必须对刻度系数误差进行标定，并予以补偿，下面就对刻度系数误差进行分析。

首先，只考虑刻度系数误差，建立误差模型为：

2.1刻度系数误差分析

在旋转的条件下，零偏可以通过旋转调制掉，并且安装误差对惯性器件产生的影响很小［6］，所以，在这里只考虑陀螺和加计的刻度系数误差对系统的影响。

由式（9）、式（10）得，在旋转条件下，陀螺和加计的误差模型可变为：

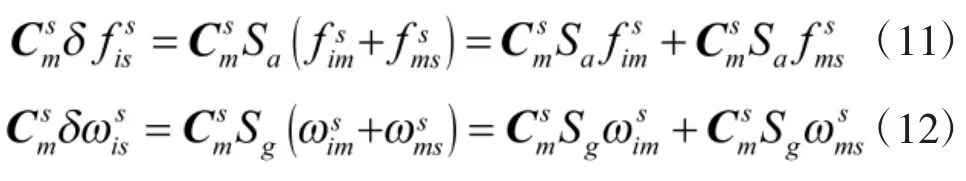
其中，f和ω为加计和陀螺的量测值，fims和ωims为主惯导相对惯性系的运动在子惯导坐标系上的投影；fmss和ωmss为子惯导相对主惯导的运动在子惯导坐标系上的投影。

由于在假设机动过程中只存在子惯导（弹丸）的横滚运动。所以，fims和ωims为极小值，可以不考虑，故在式（9）、式（10）中只考虑CmsSafmss和CmsSaωmss即可。

由式（13）看出，在弹体沿y轴旋转时，x轴和z轴的刻度系数误差Kax和Kaz在一个周期内可得到调制，并且与转动角速度ωs产生耦合，但y轴的加计刻度系数误差Kay不但不能被调制，而且不与旋转角速度产生耦合，不可观测。

由式（14）看出，在弹体沿y轴旋转时，3个方向的陀螺刻度系数误差均不能得到调制，并且x轴和z轴的刻度系数误差Kgx和Kgz不与旋转角速度产生耦合，不可观测。

综上所述，旋转对惯性器件的可观测性影响很大，在火箭炮射前准备阶段，当弹体只有横滚运动时，沿横滚轴的加计刻度系数误差不能被调制，也不可观，其他两个方向的加计刻度系数误差可观测，并且在一个转动周期内可以被调制；而陀螺刻度系数误差不能被调制，并且只有沿横滚轴方向上的陀螺刻度系数误差可观测。

2.2仿真分析

借助主惯导的速度和姿态信息作为匹配量，构建如下的状态空间模型。

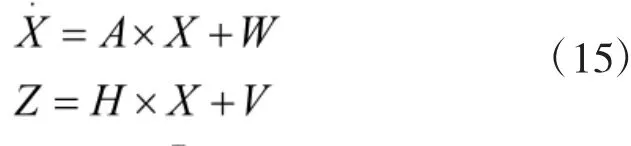
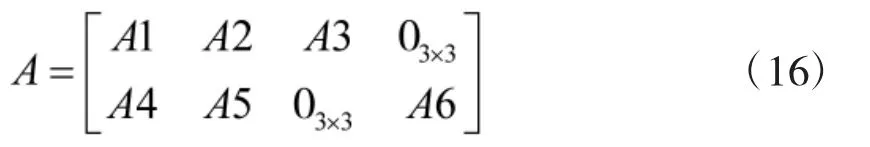
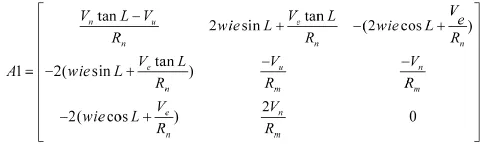
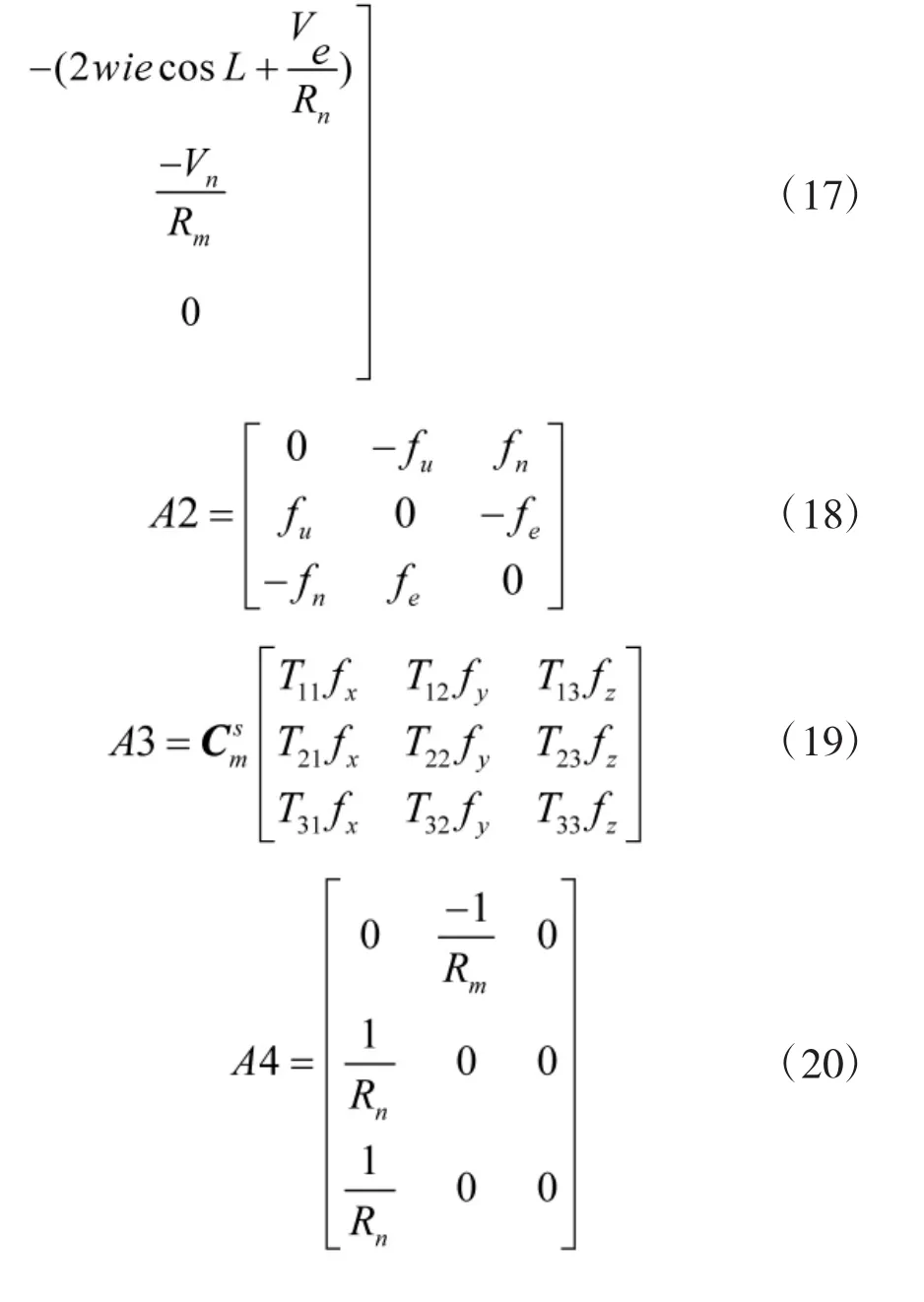
参照文献［7］将式（15）离散化以满足卡尔曼滤波要求，并设置滤波参数如下：

初始纬度为30°，经度为118°，加表刻度系数误差为10-3，陀螺刻度系数误差为10-3，状态变量X的初值都为0。

设定机动过程的运动参数如下：

前90 s，弹丸作横滚运动π/2，后90 s，弹丸横滚-π/2，加速度为0。

图1为摇架静止，弹体只有横滚运动的加计和陀螺的刻度系数误差仿真曲线（直线为设定值，曲线为估计结果）。

图1　刻度系数误差标定结果

从图1中可以看出x轴和z轴的加计，以及y轴陀螺刻度系数误差均可较好地收敛，而其余3个参数不可观测。仿真结果与2.1中理论推导的结果完全一致，表明横滚运动对火箭弹中惯性器件刻度系数误差的标定有很大影响，但是具体参数的设定需要进一步优化以减少收敛时间和提高标定精度。

3　改进标定方案设计

利用弹体的横滚运动可以将惯性器件的零偏误差分离，单独对刻度系数误差进行标定，从而提高标定精度和标定的实时性。但是由于在只有横滚运动的条件下只有3个刻度系数误差可观测，远不能满足火箭炮射在前准备阶段的标定要求。所以为了提高其他3个刻度系数误差的可观测度，提出以下方法。

第一，实验资源损耗加速。职业技术学校建设人体解剖生命科学馆，尽管服务了师生与社会，然而，实验资源的损耗加速，比如标本使用寿命缩短、空调通风系统寿命缩短、多媒体触屏学习系统使用寿命缩短等。这就要求学校有关部门对人体解剖生命科学馆设备标本的保养、维护工作给以重视。

3.1标定路径设计

因为运动方式只有弹体的横滚，所以式（11）、式（12）中fims和ωims趋近于零，不用考虑。但是，若将使摇架在3个方向上均有机动，即主惯导与惯性系有相对运动，则在进行误差分析时就需要考虑fims和ωims的影响了，原因如下：

如果fims和ωims不趋近于零，则式（11）、式（12）的第一项分别为

由式（23）、式（24）可看出，摇架在3个方向上的机动可使加计和陀螺的刻度系数误差与旋转角速度产生耦合，所以6个刻度系数误差均变为可观测，并且在式中，除沿横滚轴的惯性器件的刻度系数误差外，其余刻度系数误差均可在一个周期内得到调制。因此，主惯导与惯性系的相对运动，对惯性器件的刻度系数误差标定起着关键性作用，故设计新的机动方案如下：

首先，火箭炮摇架进行航向角变化π/2的同时进行俯仰运动π/3，并且弹丸做横滚运动π。其次，反向做相同的运动。

3.2仿真验证

按照式（15）建立状态空间模型，初始方差阵系统噪声协方差

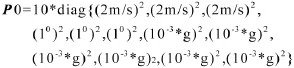
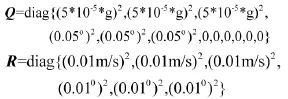
其余滤波参数与2.2中设置的相同。

图2　刻度系数误差标定结果

如图2所示，在摇架上加入3个方向的机动后，剩余的3个刻度系数误差（KayKgxKgz）均变为可观测的，其中Kay和Kgz的收敛速度较快，Kgx收敛速度较慢，不过它们的收敛性与图1相比均得到大幅提升，仿真结果证明了理论推导的正确性以及新的机动方式的可行性。表1为估计结果与事先设定值的比较。

表1　设定值与估计值对比

由表1看出，除z轴陀螺刻度系数误差外，其余参数的估计精度均能达到16%以内。

最后将文献［5］中的利用21维误差模型标定的结果与本文利用旋转调制将零偏分离的方法所得的标定结果进行比较，如表2所示。

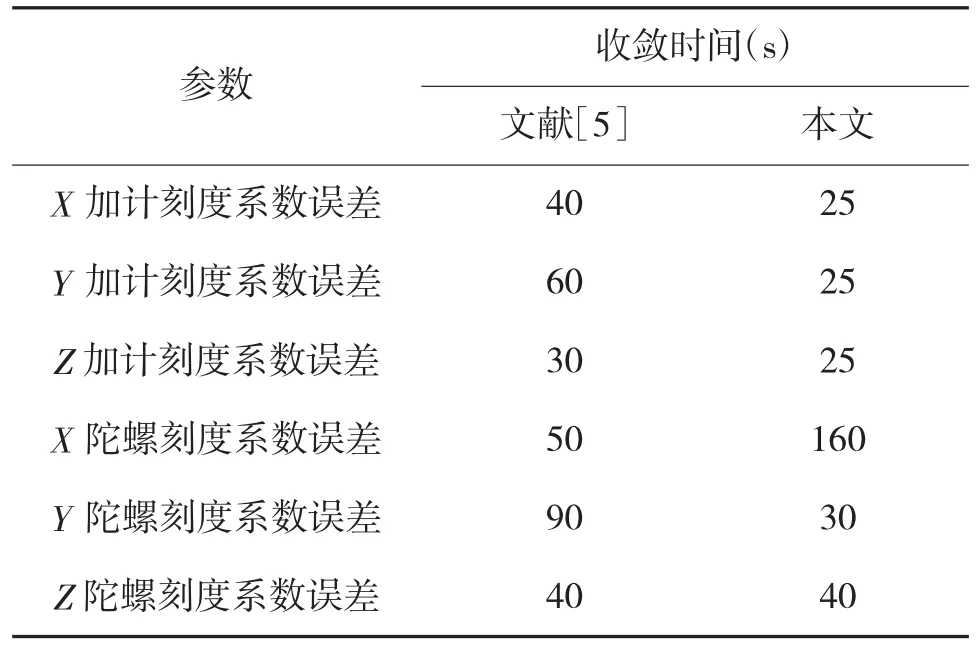
表2　收敛时间对比

表2中指出，除x轴陀螺刻度系数误差外，其余参数收敛时间较传统的标定方法都有较大提高。

以上两表分别从标定精度和估计收敛时间两个方面说明了本文所提出的标定方案的合理性。

4　结论

本文首先建立了旋转条件下的主子惯导误差模型，而后从理论上分析了弹丸的横滚运动可以使惯性器件的零偏得到调制；进而将零偏分离掉，对惯性器件的刻度系数误差的可观测性以及标定方案进行了理论分析和仿真验证，分析结果表明弹丸的横滚运动对惯组多个方向的刻度系数误差的可观测性有较大影响，仿真结果与理论分析的结论完全一致；最后，设计了新的机动方案，弥补了标定过程中只有横滚运动的不足，仿真结果表明与理论推导结果一致，并且与传统的标定方案进行了对比，也表明本标定方案的优越性，并且得出了一些具有工程应用性的结论，可为火箭炮制导化改进方案的制定提供技术支持。

总之，在弹丸旋转的条件下对火箭弹进行射前标定，不仅可以提高标定精度，而且可以提高标定的实时性，适合火箭炮的在线标定。

参考文献：

［1］SAVAGE P G.Srtapdown anaylitcs［M］.Mapel Palni，Mninesoat：Srtapdown Associaets，Inc，2007.

［2］ZHANG H，WU Y，WU M.A mutl-ipostioin cailbraiton aglorithm for niertia lmeasuremen tunits［C］//AIA A Gudiance，Navgiation and Conrtol Confeernce and Exhbiti .Honoullu，Hawaii，2008.

［3］卿立，李海强.一种中低精度捷联惯测装置的不开箱标定方法研究［J］.中国惯性技术学报，2004，12（4）：16-19.

［4］吴平，雷虎民，邵雷.一种车载筒弹惯导装置不开箱标定方法［J］.中国惯性技术学报，2010，18（1）：28-32.

［5］王志伟，石志勇，全振中.某型火箭炮捷联惯导在线标定方案研究，红外与激光工程，2015，38（1）：0266-0272.

［6］LEVINSON E，TER H J，WILLCOCK M.The next generation marine inertial navigator is here now［C］//IEEE Position Location and Navigation Symposium，1994：121-127.

［7］周大旺，赵国荣，伍国胜.主/子惯导标定中挠曲变形的ARMA补偿办法［J］.四川兵工学报，2015，26（8）：104-108.

［8］秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，2004.

Scheme of Online Calibration of Main and
Sub INS Based Rockets Rotary Motion

WANG Zhi-wei，SHI Zhi-yong，QUAN Zhen-zhong
（Ordnance Engineering College，Shijiazhuang 050003，China）

Abstract：For the preparation phase before the launch rocket can only be two degrees of freedom of angular movement but the line motion，and the need to calibrate many parameters，the model led to calibrate a large number of dimensions and poor real disadvantage. In this paper，the background of transformation guided rockets，first with the principle of rotation modulation error model is established，so that the zero-bias error inertial separation，and analysis of the rotation on the scale factor error，and the results show that the rotational motion on the scale factor error observability of significant influence. However，a separate roll motion can not motivate all six scale factor error，so the design of a new scheme of maneuver，and filtering algorithms rendering all scale factor error can be observed，and the results showed that in addition to x-axis gyro scale factor error，the remaining parameters can faster convergence. Compared with traditional methods，timeliness and accuracy of the calibration has been greatly enhanced，the importance of the rocket projectile roll motion on is fully embodied before the launch calibration.

Key words：rocket，rotary motion，main and sub INS，online calibration

中图分类号：U666.1；TJ393

文献标识码：A

文章编号：1002-0640（2016）05-0165-05

收稿日期：2015-04-09修回日期：2015-05-17

作者简介：王志伟（1990-）男，陕西华阴人，硕士研究生，研究方向：惯性导航。