基于TSS方法的雷达性能优选分析研究*

葛江涛，邓　宝，陶玉犇

（1.解放军61846部队，河北　保定072750；2.电子工程学院，合肥230037）



基于TSS方法的雷达性能优选分析研究*

葛江涛1，邓宝2，陶玉犇2

（1.解放军61846部队，河北保定072750；2.电子工程学院，合肥230037）

摘要：通过TSS方法进行了雷达性能的优选分析研究，分别针对雷达的单一性能指标和综合性能指标进行了优选分析。首先运用TSS方法完成了基于单一性能指标的雷达性能优选分析，然后通过欧几里德贴近度完成了雷达的综合性能指标优选分析，最后给出了TSS方法在雷达性能优选分析研究中的应用实例。

关键词：TSS，雷达，优选分析

0　引言

雷达作为现代国土防空的重要屏障，在战时发挥着至关重要的作用。同时，雷达作为信息时代的产物又无时无刻不在影响着我们的生活。然而，在雷达的研制、生产和使用过程中，有效地对其进行性能评估，从中进行雷达性能的优选，将直接关系到新型雷达的推广和新技术的发展。

雷达性能指标优选分析是一种涉及多学科的交叉研究范畴，不仅需要从雷达的工作原理进行研究，同时也需要从数学模型的角度对其性能进行评估优选，为研制人员或使用人员提供辅助决策。这一价值的体现主要依赖于雷达性能的优选分析，即通过对不同雷达的实验性能检测，从性能指标数据中优选较为理想的雷达。

综上所述，雷达性能的优选需要通过多部雷达的性能来体现相互差异，雷达性能的优选分析就是根据雷达的性能指标开展的分析研究。其中包括单一性能指标的优选分析和综合性能指标的优选分析。

1　单一性能指标优选分析

雷达性能的优选分析实际上就是通过一定的算法，判断各个雷达到达理想性能指标的“距离”。所谓优选分析就是通过多部雷达的性能检测，得到“距离”理想性能指标最近的雷达。

目前，对于雷达性能优选分析，应用较多的是性能指标数据的简单对比，或针对某一性能指标进行做差对比，其中不能体现雷达性能检测实验数据的随机性，缺乏对雷达性能评估的严谨性［1］。本文就是针对这一问题，将系统优选分析中的方法进行改进后应用到雷达性能优选中，提高雷达性能优选分析的科学性和可信度。在系统优选分析中应用较多的主要有Bonferroni法和TSS法［2］。Bonferroni法是以Bonferroni不等式准则为依据，进行相关的优选分析。该方法相对比较简单，但是其中人为确定因素较多。从而使得算法在不同雷达性能优选分析人员的运用过程中出现不同的标准，准确性受到质疑。TSS法，则可较好地弥补Bonferroni法的不足。

但将TSS法运用于雷达性能优选分析，需要对其进行一定的改进。因为TSS法定义优选分析结论的依据是“越大越好”或“越小越好”，但雷达性能除通过新技术以外的提高是以一定的附加代价换取的，过分地追求高性能就需要牺牲付出更多的代价，并且超越雷达基本性能需求的“高性能”可能是得不偿失的。因此，达到代价与性能兼顾且满足应用要求是最为理想的状态。本文在将TSS法引入雷达优选分析中的同时，也对其进行了一定的改进，加入了“距离”的概念，得到最小“距离”者为最优性能雷达。

1.1算法基本思想

所谓TSS法也就是Two-stage Sampling Method，即通过两次抽样来计算雷达性能指标，该方法可以利用少量的实验性能检测次数得到大量实验性能检测的准确度，大大减少在实验检测中消耗的资源。

对于TSS法的运用，首先需要定义两个概念。①将能够“正确选择”最优雷达的过程命名为事件，并且考虑到其中的随机性，定义CS事件发生的概率为P*。②对于多部雷达中的某两部雷达可能各指标的性能基本相当。在此提出“误差容忍量d*”，即当两部雷达性能指标相差在d*范围内，则认为均为最优。

TSS法的基本思想为：将K部雷达进行多次实验性能检测，采集针对某一性能指标的第i部雷达第j次实验性能检测的样本值Xij，进而计算出其中部分样本的均值Xi（1）和方差Si2。由此可以计算出TSS法总共需要的抽样次数（实验性能检测次数），即第2次需要的抽样次数（实验性能检测次数）。进一步求取第2次抽样样本的均值Xi（2），以及第1次、第2次分别抽样的权重。再将Xi（1）和Xi（2）综合计算可以得到针对该性能指标的估计值。最后进行欧几里德贴近度的计算，得到该雷达优选分析的评估值。

1.2确定抽样总次数

对于TSS法中抽样总次数（实验性能检测总次数）的确定，也就是该算法的第1次抽样。根据算法基本思想中确定的两个概念，对于CS事件发生的概率P*，根据数理统计和雷达性能检测中的普遍应用，取值90%；而“误差容忍量d*”的确定，则是根据大量随机数据基本服从的正态概率分布。根据正态概率分布90%的分布区间和“误差容忍量d*”的实际操作应用，可将“误差容忍量d*”定为Si/3，即d*=Si/3。

运用TSS法解决雷达性能指标优选分析，需要分别对K部雷达进行实验性能检测，然后分别进行两次性能指标的抽样。第1次抽样一般使用的采集样本数应固定且为已采集实验样本数的一半，然后利用方差估计结果确定第2次抽样计算应具备的实验样本数。

假定通过实验性能检测已采集性能指标样本数为Ni（i=1，2，…，K）且Ni≥20［3］。在第1次抽样的计算中，取ni1=Ni/2次性能指标样本，分别得到均值和方差为。从而得到TSS法总共需要的雷达实验性能检测样本数为Ni0：

其中，hi的取值由优选分析的雷达部数K、正确选择CS事件的概率P*以及第1次抽样使用的性能指标样本数ni1三个参数联合查表1得到。

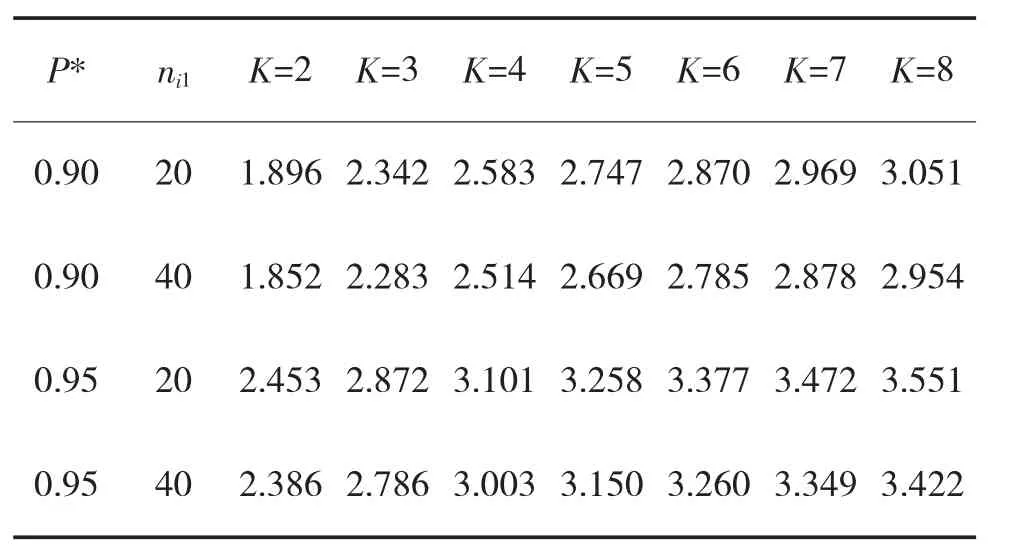
表1　“TSS法”参数表

如果Ni≥Ni0，可直接进行第2次抽样的计算；否则需要继续进行雷达性能检测实验，采集性能指标更多的样本数据

1.3优选分析

在第2次抽样的计算中，根据第1次抽样计算得到需要的总实验样本数Ni0，可知第2次抽样需要性能指标样本数为（Ni0-ni1）。由此，得到第2次抽样的性能指标样本均值为：

在完成第1次、第2次抽样的性能指标样本均值计算的基础上，需要分别确定两次抽样的权重，进行两次抽样的结果合成为针对该性能指标在置信度P*情况下的最优雷达。

权重的计算为：

加权计算得到：

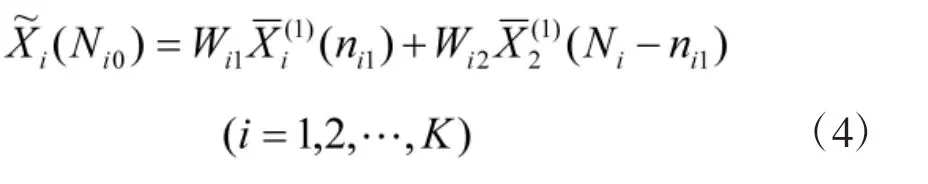
在得到的基础上，可以将与理想性能雷达进行比较，最为接近的雷达即为最优雷达。

2　综合性能指标优选分析

当对雷达进行综合性能指标优选分析时，每个雷达均包含X、Y、…、Z共m个性能指标，且每一性能指标根据在雷达综合性能指标优选分析中的重要程度分别确定为权重ω。此时，基于综合性能指标在相应权重下的欧几里德贴近度得出优选结果［4］。即计算该雷达的各个性能指标分别在一定权重下与理想雷达的距离。

得到具有最小Li的雷达是综合性能指标以置信度为P*的最优雷达。

当m=1时，得到具有最小Li的雷达是针对某一性能指标且置信度为P*的最优雷达。

3　应用实例

通过雷达性能优选分析可以形象直观地表现出雷达性能，所谓优选分析也就是选取可以较好地满足使用需求的雷达、达到或接近理想目标的雷达。以机载预警雷达性能优选分析为例［5］，在对其进行优选分析中，综合运用单一性能指标优选分析和综合性能指标优选分析，充分体现TSS法在雷达性能优选分析的过程。

选取机载预警雷达中的4部雷达分别为雷达1、雷达2、雷达3和雷达4，其中性能指标均为预警时间、目标识别能力、抗干扰能力（5次干扰）、可靠性（故障次数）和可用性（故障时间）。假定理想雷达的性能指标值分别对应为10（min）、10（个）、3（次）、15（次）和25（min）。

将4部雷达分别进行40次实验性能检测，取其中的20次实验结果作为第1次抽样的性能指标样本。计算得到“预警时间”单一性能指标第1次抽样的性能指标样本均值，同时第2次抽样仍需要41次实验结果作为性能指标的样本。进而计算得到第2次抽样的样本均值和第1次、第2次抽样的样本均值权重分别为0.386 9和0.613 1。将两次抽样的结果进行综合得到仿真结果如图1所示。仿真结果与理想目标值比较，得到雷达预警时间性能指标优选分析残差图如图2所示。

通过优选分析可知：雷达3最接近理想目标，在4部雷达中以置信度90%达到最优。

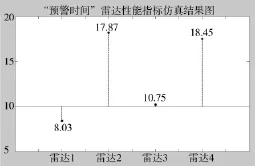
图1　“预警时间”雷达性能指标仿真结果图

图2　“预警时间”雷达性能指标优选分析残差图

雷达综合性能指标优选分析则将5个性能指标综合考虑，仿真结果如下页图3所示，各曲线分别表示各部雷达的性能指标值和理想性能指标值；在对5个性能指标进行欧几里德综合距离计算时，将其视为同等重要，即权重一致均为0.2，得到优选分析距离图如图4所示。

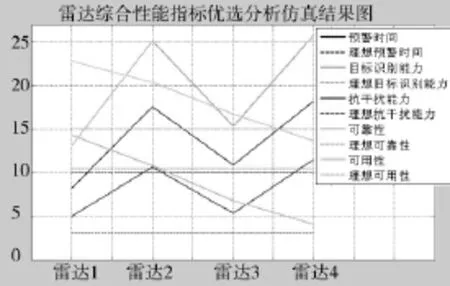
图3　雷达综合性能指标仿真结果图

图4　雷达综合性能指标优选分析距离图

通过优选分析可知：雷达1以置信度90%达到4部雷达中的最优。

4　结论

雷达性能优选分析可以有效地进行雷达的性能仿真和评估，一定程度上为研究人员提供了可信的决策支持。尤其是将TSS法应用于雷达性能的优选分析中，使得雷达性能优选更具科学性和准确性。但是，就目前雷达性能优选分析的研究情况而言，尚有较大的发展空间，这不仅是雷达研究领域前进的方向，更是多学科交叉研究相互融合的努力方向。

参考文献：

［1］胡中泽，曹菲.雷达抗干扰性能的评估模型研究［J］.电子设计工程，2012，20（24）：134-136.

［2］肖田文，范文慧.系统仿真导论［M］.北京：清华大学出版社，2010.

［3］王鹤磊.一种雷达系统效能的综合评估模型［J］.系统工程与电子技术，2001，23（3）：40-50.

［4］杨纶标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，2008.

［5］唐政，高晓光.机载雷达探测系统效能评估模型分析［J］.火力与指挥控制，2007，32（11）：21-23.

Optimization Analysis of Radar Properties Based on TSS Method

GE Jiang-tao1，DENG Bao2，TAO Yu-ben2
（1.Unit 61846 of PLA，Baoding 072750，China；2.Electronic Engineering Institute，Hefei 230037，China）

Abstract：Aiming at the TSS method which is used in the optimization analysis of radar，the article has researched the optimization analysis of single radar properties indicators and comprehensive radar properties indicators. It is the method of TSS Method and Euclid which helps us calculates the optimization analysis of radar properties indicators. Finally，efficiency and simulation of the optimization analysis of radar properties is achieved in order to check the TSS method.

Key words：Two-stage sampling method，radar，optimization analysis

中图分类号：TN953

文献标识码：A

文章编号：1002-0640（2016）05-0161-04

收稿日期：2015-05-15修回日期：2015-06-27

*基金项目：全军军事类研究生基金资助项目（2014JY328）

作者简介：葛江涛（1990-），男，河北邯郸人，助理工程师。研究方向：作战仿真实验数据分析。