基于粒子群算法维修保障单元优化配置*

周辅疆，顾　赟，王　斌，陈宏文，洪啸虎

（镇江船艇学院，江苏　镇江　212003）



基于粒子群算法维修保障单元优化配置*

周辅疆，顾赟，王斌，陈宏文，洪啸虎

（镇江船艇学院，江苏镇江212003）

摘要：针对维修保障单元配置过程中需权衡综合多因素问题，提出了一种基于粒子群算法的维修保障单元优化配置决策模型和方法。首先，以维修任务完成概率为设计目标、以维修保障单元总数量为约束，建立维修保障单元配置决策模型；其次，运用粒子群算法对维修保障单元配置问题进行优化求解。通过具体实例分析，证明了该方法的正确性和有效性。

关键词：粒子群算法，维修保障单元，配置，模型

0　引言

近几场信息化战争的实践表明，体系之间的对抗不仅依赖于装备本身优良的战技性能，而且更依赖于其装备保障系统各保障点内维修保障单元合理有效的保障。维修保障单元优化配置是装备维修保障工作的一项重要内容，是保持和恢复装备战技性能、提高装备维修保障综合效益的重要保证［1］。维修保障单元在各保障点配置过程中，保障点的部署地域、待维修装备类型与数量都不相同，如何考虑保障的有效性、及时性和部署性，权衡各方面因素，合理地配置不同类型维修保障的数量，使维修保障点能够适时、适地、适量、精确地提供保障，必须要建立优化配置模型，科学定量地优化配置。

国内外很多学者对粒子群算法与应用进行了深入的研究。文献［2］对国外粒子群算法进行了全面综述，文献［3-5］对粒子群算法在各领域的应用进行了全面综述。理论与实践应用表明，粒子群算法对那些多约束、多目标、非线性的优化问题具有极大优势和良好求解效果，所以此方法同样可用于复杂的维修保障单元优化配置问题。

1　问题描述及模型建立

1.1问题描述

维修保障单元就是将所需的维修保障人员、维修保障器材、维修保障装备等组合而形成的要素齐全、功能匹配的、最小的、不可拆分的维修资源集合，是维修保障系统中的最小保障实体。不同的维修保障单元具有不同的组成要素和维修能力，不同保障点内根据维修保障需求配置不同种类的基本维修保障单元。针对不同的作战任务而言，维修保障单元在各保障点配置过程中对系统维修任务完成程度、维修保障单元利用程度和数量等要求侧重点不同，但是同时要满足所有目标的优化是特别困难的，只能根据具体现有保障条件，采用科学合理设计与优化方法对维修保障单元进行配置，使设计和优化的维修保障点更能在规定的时间内和有限的保障资源条件下更加高效地完成维修保障任务。本文以维修任务完成概率最大优化目标、以维修保障单元数量总约束，构建维修保障单元配置决策模型并进行优化配置。

以执行某次作战任务各维修保障点维修保障单元优化配置为例，设整个作战任务中的作战指挥层次共有H层，每一层指挥层次为h，其中h=1，2，…，H，每一指挥层次所属作战单元共有Q个。第h指挥层上第q个作战单元可用Zqh表示。装备共J种，其数量分别为C1，C2，…，Cj，…，CJ。第q个作战单元Zq中拥有的第j种装备数为C'q，j，其他种类参数装备数量为C'q，1，C'q，2，…，C'q，J。已知第q个作战单元第j种装备战损率为pq，j，第q个作战单元第j种装备中第i故障单元的损坏比例为sq，j，i，全部装备中可修复故障单元种类总数为N种，各故障单元分别表示为U1，U2，…，Ui，…，UN，故障单元可用集合U= ｛U1，…，Un，…，UN｝表示；第j种装备中可修故障单元可表示为Uj，共含有种类总数为Ij，故障单元用集合表示为Uj=｛Uj，1，…，Uj，i，…，Uj，Ij｝⊂｛U1，…，Un，…，UN｝，其中1≤i≤Ij≤N。可承担装备故障单元的维修保障单元用XU表示，共有K种类型的维修保障单元，其可分别表示为XU1，XU2，…，XUk，…，XUK，第k种维修保障单元XUk可承担的故障单元种类集合为Uj=｛Uj，1，…，Uj，i，…，Uj，Ij｝⊂｛U1，…，Un，…，UN｝，其中Ij≤N。建模前先作如下设定：

1）现有给定约束的第k种维修保障单元数量为MXU'k规，按照利用率设计标准范围值为ψ标=1、运用维修保障单元利用率与数量为约束而设计出来的维修保障系统需要第k种维修保障单元数量为MXU'（k），且MXU'k规＜MXU'（k）。

2）设计后系统内有Q个不同指挥层次上保障点ZB1，…，ZBq，…，ZBQ，承担第k种维修保障单元修理的维修任务，保障点ZB1，…，ZBq，…，ZBQ，承担来自于Q个作战单元的维修任务数量分别为CU'1，q，k，…，CU'1，q，k，…，CU'1，Q，k，保障点ZBq内第k种维修保障单元实际平均保障服务时间为MMDTqk；

3）各保障点承担各类维修任务的优先级别都相同，各保障点内维修保障单元采取即坏即修的方式，并实行并行修理的方式，维修遵从先到先服务的规则，当所有维修保障单元都正被占用，维修任务在队列中等待维修；

4）维修任务的到达分布是根据实际维修任务分布而确定的，维修任务到达是相互独立的，且到达时间间隔服从随机型分布；

5）某一类型的维修保障单元能修理多类不同类型装备不同的故障单元，不同类维修保障单元修理的维修任务不重叠，各类维修保障单元实行并行修理的方式。

1.2维修保障单元配置模型建立

目标函数：建立以整个维修保障系统维修任务完成概率为设计目标、以维修保障单元总数量为约束的保障点维修保障单元配置决策模型，将有限的维修保障单元配置到系统的各个保障点内，以实现系统内各保障点完成维修任务最大的优化目标，从而达到维修保障单元最优配置目的。因此，维修任务完成概率为优化目标的各保障点维修保障单元优化配置目标函数为：

式中：MXU''q，k为保障点ZBq实际配置维修保障单元数量为各保障点维修任务完成概率优化模型的决策变量；T 'q，k为保障点ZBq内第k种维修保障单元完成分配维修任务所需要的维修时间；MXU'q，k为保障点ZBq完成分配维修任务需要配置数量；MMDTq，k为保障点ZBq内第k种维修保障单元完成分配维修任务的实际平均保障服务时间。fk为Q个维修保障点的维修任务完成概率。

约束条件：

1）保证配置到Q个维修保障点第k种维修保障单元数量之和为现有维修保障单元的总数：

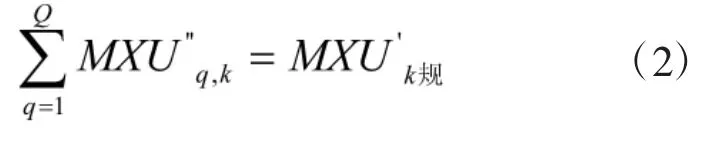
2）保障点ZBq承担分配维修任务的数量：

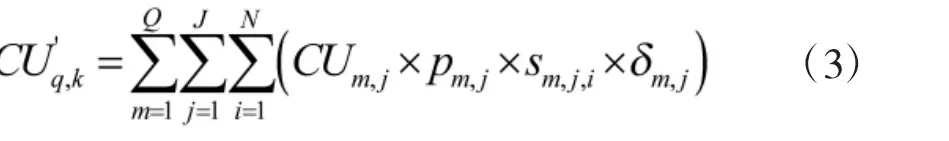
3）第k种维修保障单元修理各种维修任务的平均保障服务时间：

4）完成维修任务所需要的维修时间：

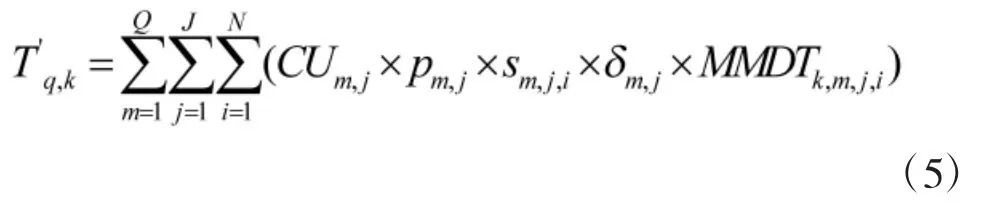
5）由第k种维修保障单元修理作战单元第j种装备第i个故障单元的平均保障服务时间：

6）维修保障点ZBq完成维修任务实际所需要维修保障单元数量：

7）系统所有保障点完成该维修任务所需维修保障单元数量：

8）所需维修保障单元数量大于目前现有维修保障单元的数量：

9）在维修保障单元数量不足的情况下，保障点ZBq内第k种实际配置的维修保障单元数量不能超过所需要的数量

2　粒子群算法优化配置方法

维修保障单元或维修保障资源优化配置方法主要有传统配置方法和智能优化配置方法。传统的配置方法主要依照最优化理论来进行配置，如枚举法、线性规划法、非线性规划法和动态规划法，但传统配置方法主要存在着需要简化为相应配置数学模型，才可能使优化配置的结果达到技术上的可行解，而且不能保证一定是最优配置方案。因此，在数量有限的维修保障资源约束下，探索更为有效的配置方法寻求维修保障资源最优配置方案实现维修任务完成概率最大化已被越来越多的国内外研究机构所关注。

智能优化算法主要有模拟退火法、人工神经网络、蚁群优化算法和粒子群算法等。粒子群算法是一种模拟鸟群社会行为的群体搜索算法，它通过群体中粒子间的合作与竞争产生的群集智能指导优化搜索［6］。它与模拟退火、遗传算法等相比，优势在于没有复杂的交叉和变异操作，结构简单、控制参数少、容易实现并且收敛速度快的特点。所以，针对上速算法存在的问题，本文基于粒子群算法对维修保障单元进行优化配置。

2.1粒子群算法原理

粒子群算法采用随机的方式为种群中各个粒子产生初始速度和位置，然后通过迭代逐渐找到最优解。在每一次搜索过程中，粒子通过跟踪两个最优值来更新自己：一个是粒子本身所找到的最优解，即个体最优解；另一个是整个种群目中找到的最优解，称之为当前全局最优解［7-8］。如在一个X的多维搜索空间中存在M个粒子组成的一个种群，其中粒子y是当前的空间位置为Ny=（ny1，ny2，…，nym），m=1，2，…，M，粒子y的当前飞行速度为Vy=（vy1，vy2，…，vym），粒子y经历的每一种个体最优解为muy=（muy1，muy2，…，muym），粒子的全局最优解为mu。根据粒子群更新公式和搜索机制可以搜索出全局最优解为mu。

2.2基于粒子群算法对该问题优化配置

各维修保障点内维修保障单元运用粒子群算法优化配置设计步骤如下：

1）算法步骤

第1步是产生初始粒子群，评价初始粒子群粒子，确定粒子的个体极值pi、全局最优pg；

第2步是迭代次数加1，对粒子进行更新；

第3步是对整个种群进行评价，确定粒子的个体极值pi和整个种群中的全局最优pg；

第4步是判断是否满足算法结束条件，若是则转下步骤，否则转上第2步骤；

第5步是利用已知全局最优解生成项目（维修保障单元）配置方案，算法结束。

2）粒子表示

采用基于向量的粒子表示方法，即xi=［xi，1，…，xi，q，…，xi'，Q］，i∈｛1，2，…，N｝（N为粒子个数），每个粒子对应一个方案；粒子维数为Q；xi，q表示第q个维修保障点第K种维修保障单元，xi，q∈［0，aq］。

3）适应度计算

适应度函数用来评价群体中个体的优劣，其数值引导着粒子群的移动方向与速度。粒子的适应度计算公式如下：

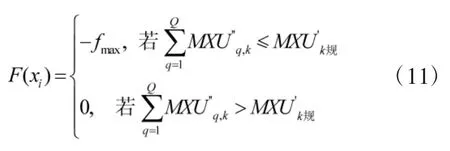
如果配置方案满足维修保障单元总量约束条件，则粒子的适应度取模型目标值的负数（因为粒子群算法优化的目标是获得最小值）；否则取0。

4）粒子更新

算法采用的粒子更新公式为：

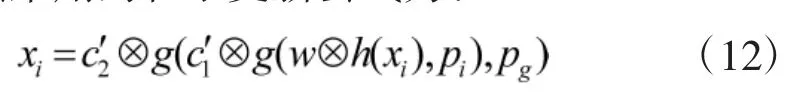
其中：h（xi）表示对粒子xi执行扰动操作，g（xi，pi）和g（xi，pg）都表示两个粒子相互作用，产生一个新粒子。式（12）由以下部分构成：

一是粒子对目前状态的思考，即

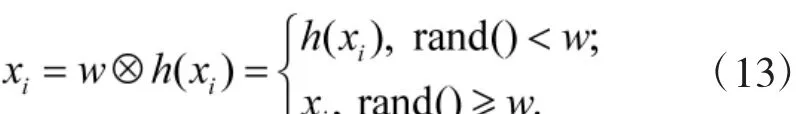
二是粒子从pi继承信息

三是粒子从pg继承信息

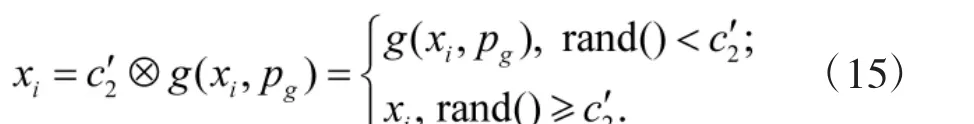
其中，c'1、c'2、w为算法控制参数。粒子的扰动和粒子的信息继承可分别采用变异或交叉来实现。

四是粒子的扰动。在此引入一种基于任务序列的随机插入法对更新后的粒子xi进行扰动。该方法分为：在［1，Q］范围内随机生成两个整数u1、u2；xi，u1取［0，a u1］范围内的任一不同于原来值的数，则xi'，u1=1，否则xi'，u1=0；同理xi，u2取［0，a u2］范围内的任一不同于原来值的数。

五是粒子的信息继承。在此采用粒子更新方法。参与信息继承的两个粒子，一个粒子为x1，另一个粒子为x2，经交叉运算产生的一个新粒子分别为x'。在1到Q之间产生一随机整数a，x'的前a维继承x1，即x'j=x1j，j=1，2…a；而从a+1到Q的后Q-a维则来源于x2，即x'j=x2j，j=a+1，…Q。

3　应用实例

3.1参数设定

假设整个作战任务中的作战指挥层次共有H=4层，任意指挥层次以h表示，其中h=1，2，…，4，指挥层次所属作战单元共有Q=10个。该维修保障系统首先采用维修保障单元利用率与数量有约束的设计方法，设计后系统内有不同指挥层次上保障点承担第k种维修保障单元修理的维修任务，现有给定约束的第k种维修保障单元数量为MXU'k规= 30，T规定=10 h，βk=0.8，按照利用率设计标准范围值为ψ标=1、运用维修保障单元利用率与数量有约束设计方法而设计出来的维修保障系统需要第k种维修保障单元数量为MXU'（k）=45，设计后系统内有10个不同指挥层次上保障点，ZB1，…，ZBq，…，ZB10。承担第k种维修保障单元修理的维修任务。各保障点承担维修任务数量、平均保障服务时间、实际应配置的维修保障单元数量等其他各参数如表1所示。

表1　各维修保障点的基本信息

3.2结果分析

本节采用Matlab编写粒子群算法程序，在计算机配制为Pentium4 CPU3.2 GHz内存为2 G和Windows—XP操作系统时，粒子群算法的平均计算时间为10 sec，其中种群规模为10个粒子，迭代次数为200代，w为0.5，c1为0.5，c2为0.5，模拟次数为1 000次时，此时各保障点完成维修任务概率最大值为0.9024，各保障点配置第k种维修保障单元数量分别是：ZB1h=4，ZB2h=3，ZB3h=4，ZB4h=3，ZB5h=1，ZB6h=3，ZB7h= 4，ZB8h=3，ZB9h=3，ZB10h=2，共需要k种维修保障单元数量为30个。

为了验证粒子算法在处理维修保障单元优化配置问题，利用了基于遗传算法与本文所提出的基于粒子算法应用于维修保障单元优化模型优化配置时各项参数对比，如164页表2所示。

从表2中显示看出，基于粒子群算法对维修保障点进行维修保障单元优化配置时，其性能优于遗传算法。本文所提算法的平均迭代次数为200次，

表2　基于粒子算法与遗传算法优化配置参数比较

而遗传算法需要220次，粒子群算法比遗传算法节省了55.7%的寻优时间；且运用粒子群算法进行配置的维修保障点完成维修任务的概率比前者高23.8%，而所需维修保障单元的数量减少6.25%。因此，仿真实验结果表明，利用粒子群算法进行维修保障单元优化配置的优越性更加明显。

参考文献：

［1］张涛.装备使用阶段维修保障能力评估建模与分析［D］.长沙：国防科技大学，2005.

［2］MARGARITA R S. Multi-objective particle swarm optimizers：a survey of the state-of-the-art［J］. International Journal of Computational Intelligence Research，2006，2（2）：287-308.

［3］倪庆剑，邢汉承.粒子群优化算法研究进展［J］.模式识别与人工智能，2007，20（3）：349-357.

［4］薛洪波，伦淑娴.粒子群算法在多目标优化中的应用综述［J］.渤海大学学报：自然科学版，2009，30（3）：265-269.

［5］胡伟，徐福缘.基于改进粒子群算法的物流配送中心选址策略［J］.计算机应用研究，2012，29（12）：4489-4491.

［6］陈君兰，叶春明.粒子群优化算法在柔性资源受限项目调度中的研究［J］.计算机科学，2013，39（2）：241-245.

［7］张丽红，赵鸣博，王晓凯.基于粒子群算法的彩报印刷墨量计算方法研究［J］.计算机测量与控制，2011，19（3）：651-657.

［8］陈光亚.基于主成分分析法的炮兵装备维修保障优化模型［J］.四川兵工学报，2014，25（12）：88-91.

［9］孟非，黄太安.一种简化粒子群算法及在三维装箱问题中的应用［J］.科学技术与工程，2013，31（13）：9214-9218.

Optimal Allocation of Maintenance Support Union Based on Particle Swarm Optimization

ZHOU Fu-jiang，GU Yun，WANG Bin，CHEN Hong-wen，HONG Xiao-hu
（Zhenjiang Watercraft College，Zhenjiang 212003，China）

Abstract：The paper proposes a method and a model of optimal allocation of maintenance support union based on particle swarm optimization. Firstly，it establishes the decision model of allocation of maintenance support union with the goal of maintenance mission completion probability and with the quantity restriction of maintenance support union. Secondly，it adopts the method of particle swarm optimization to solve the problem of allocation of maintenance support union. According to analyze the example，it proves the correctness and effectiveness of the proposed method.

Key words：particle swarm optimization，maintenance support union，allocation，model

中图分类号：TP311

文献标识码：A

文章编号：1002-0640（2016）05-0157-04

收稿日期：2015-05-05修回日期：2015-06-17

*基金项目：军队技术基础课题资助项目（X字第2011759）

作者简介：周辅疆（1975-），男，湖南衡阳人，博士，讲师。研究方向：船艇装备保障。