基于贝叶斯模型的装备剩余寿命预测研究
刘 刚,黎 放
(1.海军工程大学,武汉 430033;2.海军工程大学舰船综合保障工程研究室,武汉 430033)
基于贝叶斯模型的装备剩余寿命预测研究
刘刚1,2,黎放1,2
(1.海军工程大学,武汉430033;2.海军工程大学舰船综合保障工程研究室,武汉430033)
摘要:为了解决武器装备日益复杂及维修工作日趋繁重的问题,运用贝叶斯模型预测装备修理后的剩余寿命,为合理安排其修理计划提供依据。替代传统的指数分布,用威布尔分布描述系统寿命特征,并运用极大似然方法和贝叶斯方法估计威布尔分布的两个未知参数,给出其置信区间。在此基础上,对先验样本和后验样本两种不同情况,分别运用贝叶斯模型预测装备修理后的剩余寿命,并给出实例。结果表明了该方法的有效性。
关键词:威布尔分布,贝叶斯,剩余寿命,预测
0 引言
近年来,随着科技水平的不断发展,武器装备现代化、模块化程度不断增加,采取传统的维修模式已经不能适应新装备的维修保障要求。对于装备的使用人员或直接维修人员而言,传统的预防性维修、视情维修策略越来越不能满足装备保障现代化保障需求。而采取基于状态的维修(Condition-Based Maintenance,CBM)则能减少维修费用,最大化利用装备[1-2]。因此,对装备的运行状况进行监控,提前发现装备的故障征兆,采用合适的方式进行修理,预测装备的剩余寿命,这对于提高装备可用性、降低维修消耗具有重要的理论和现实意义。
一般认为复杂的机电产品寿命分布函数如同电子产品一样,是服从指数分布的。但实践证明,只有小部分复杂的机电产品寿命分布函数是服从指数分布的,大部分是服从威布尔分布的,通过威布尔分布的研究,指数分布只是其特殊形式。因此,对于武器装备而言,运用威布尔分布描述其寿命分布函数,更加合理、准确。目前,威布尔分布被广泛运用于航天航空、机械制造、生物医学等领域[3-5]。
因此,针对以上情况,本文研究运用威布尔分布描述系统使用寿命,研究运用极大似然方法和贝叶斯方法来求解威布尔分布的两个未知参数,同时求得这两个参数的贝叶斯置信区间;基于不同的分析样本,运用贝叶斯模型预测系统在修理后的剩余寿命,从而为使用和维修人员合理安排装备的使用与维修计划提供合理依据。
1 威布尔分布
威布尔分布的概率密度函数和分布函数如下所示:


其中,v是形状参数,β是尺度参数。当v>1时,威布尔分布的值是递减的;当v<1时,威布尔分布的值是递增的;当v=1,威布尔分布就成了指数分布;当v≥3.5时,其曲线趋于正态分布的情况。因此,可以看出,威布尔分布是比指数分布、正态分布更一般的分布,可以更加准确描述复杂系统的寿命特征。
为了研究的方便,令θ=1/βv,则式(1)和式(2)可表示为:

2 问题描述
假设系统使用寿命服从威布尔分布,内嵌BIT监控其运行状态,其中在运行过程中,可能会发生n个故障,为了使系统运行状况最优,其中m个故障可能需要提前修理。当系统运行到时间点x1时,r1个故障被修理;到时间点x2时,r2个故障被修理;直到时间点xm,rm=n-r1-r2-…rm-1-m个故障被修理为止。因此,修理的时间点集X=(x1,x2,…,xm),对应时间点故障数量集为R=(r1,r2,…,rm)。在本文中,针对该系统,研究运用极大似然方法和贝叶斯方法估计威布尔分布的参数值,并确定其置信区间,将其用于预测系统的剩余寿命。
3 参数估计
在运用威布尔分布的过程中,由于θ和υ这两个参数都是未知的,无法直接利用。一般情况下,可以利用系统运行过程中积累的观测数据来估计未知的参数,因此,文中基于这种思路,运用极大似然方法来分析威布尔分布的两个参数,同时利用贝叶斯模型分析威布尔分布的平方误差损失和置信区间。
3.1极大似然估计
设系统运行过程中的观测数据为(x,r),则其似然函数为:


对于极大似然函数,分别对θ和v求导,并使求导后的公式为0,得到:


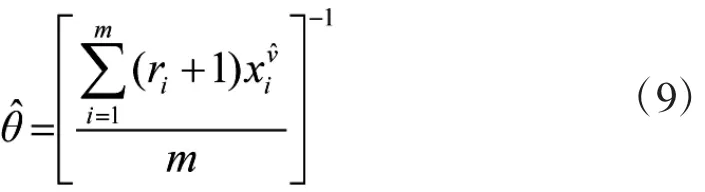
将式(9)代入式(8),可以得到的极大似然估计可以通过下式求出:



通过式(11)~式(13)可以得到矩阵I(θ,v),在一般情况下,(,)的极大似然估计近似于均值为(θ,v),协方差为I-1(θ,v)的正态分布,即:

其中I0(θ,v)为以下矩阵:

3.2贝叶斯估计
极大似然估计所利用的信息一般都是已有的信息,俗称先验信息,这些信息反映的是系统历史运行状况,虽然一定程度上能反映系统未来的趋势,但是不够全面;而贝叶斯估计除了能利用先验信息以外,还能模拟产生系统未来的运行信息,俗称后验信息,将先验信息同后验信息结合起来,共同估计θ和v的参数值,得到的参数值能更加全面反映系统的寿命特征[6-9]。
假设θ和v有如下先验形式:

其中a,b,c,d都是正实数。
通过式(5)和式(14),可以得出参数θ和υ的先验分布如下:

其中:

同时分别求出θ和v后验边缘分布:

基于平方误差损失,参数θ和v的贝叶斯估计值为:

可以看出,估计值中含有复杂的积分函数Φ(a,c,x),因此,考虑运用林德利近似法来计算贝叶斯估计值,计算公式如下:

考虑到有2个参数的情况,令u(λ)=(λ1,λ2),其平均值近似为:
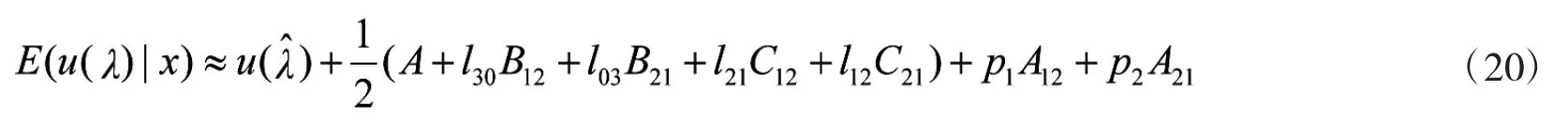
其中:

此处,ij为先验信息矩阵的倒置矩阵的第i行第j列的值,L为先验数据的极大似然函数。式(20)中未知参数(λ1,λ2)的极大似然估计值为(1,2)。
令u(λ)=(θ,v),则有:

其中Iij为先验信息矩阵的第i行第j列的值。

根据林德利近似法,参数θ和v的贝叶斯估计值为:

3.3贝叶斯置信区间
假设函数g(θ,v)的置信水平为100(1-γ)%,其贝叶斯置信区间为(Lg,Ug),则(Lg,Ug)需满足以下条件:

实际应用中一般用γ/2代替γ。
通过式(16)和前面的计算,假设参数v的置信水平为100(1-γ)%,则其置信区间(Lv,Uv)可以通过下式求解:

其中,

同理,θ的置信区间(Lθ,Uθ)可以通过下式求解:

其中,

4 基于多样本的贝叶斯预测
贝叶斯估计可以同时利用先验信息和后验信息,因此,在样本的选取中,基于先验信息的样本可以简称为先验样本,基于后验信息的样本可以简称为后验样本[10-14]。在本节,将分别讨论基于先验样本和后验样本来开展系统运行时间的贝叶斯预测。
4.1基于先验样本的预测
令Ys表示系统更换备件后的运行时间,其中Ys=Xm+s,s=1,2,…,rm。当X=x时,Ys的概率密度函数为:

其中,R(·)=1-F(·|θ,v)为服从威布尔分布的生存函数,κ为归一化常数,满足
通过式(23)和式(15),可以得到基于先验样本的分布函数为:

因此,基于先验样本预测的生存函数为:


因此,通过对先验样本分析,及求解下列公式,可以得到置信水平为100(1-γ)%时,Ys的置信区间为(L1,U1)。
P(Ys>U1|x)=γ/2,P(Ys>L1|x)=1-γ/2
4.2基于后验样本的预测
在很多工程应用领域,分析人员一般希望在现有数据的基础上,对系统未来的运行状况进行预测,即运用来自相同的寿命时间分布的一组规模为N的后验样本预测修理后系统的运行时间。令Ti(i=1,2,…,N,T1<…<TN)为基于规模为N的后验样本的系统运行时间,如式(3)所示。s个顺序统计量的概率密度函数如下所示:

通过式(25)和式(15),可以得到基于后验样本的分布函数为:

相应地,其生存函数为:

因此,通过后验样本分析,求解下列公式,可以得到置信水平为100(1-γ)%时,Ts的置信区间为

5 算例
为了验证本文提出的方法的有效性,对某型设备开展具体试验分析,下面是该型设备在不同条件作用下记录下来的数据,该数据服从威布尔分布[15]。从观测样本n=19中随机挑选规模m=8的样本,具体数据如表1所示。
利用式(9)和式(10)进行计算,可以分别求出θ和v的极大似然估计值=0.114 8,=0.974 3。假设(θ,v)的先验分布是式(14)所描述的两变量分布,令参数a=0.1,b=0.5,c=1.5,d=15。利用式(18)和式(19)进行计算,可以分别求出θ和v的贝叶斯估计值B=0.116 7,B=0.973 6。利用式(21)和式(22)进行计算,运用林德利近似法,分别求出θ和v的贝叶斯估计值L=0.112 1,L=0.984 9。同时,可以求得在置信水平为95%时,θ和v的置信区间分别是(0.0370,0.245 8)和(0.515 5,1.527 7)。

表1 试验中挑选的样本数据
置信水平为95%时,在先验样本的数据条件下,系统的贝叶斯估计剩余寿命分布和寿命时间间隔。通过先验样本,得到剩余寿命分布函数,从该分布中生成一组规模N=5的后验样本。通过对后验样本进行分析,s(1≤s≤5)个故障被修理后,系统剩余寿命的贝叶斯估计间隔预测与实际值的对比如下页表2所示。
可以清晰地看到,随着s的增加,估计的间隔长度也随之增大,即系统的剩余寿命也越长;通过对比分析,根据后验样本预测的系统的剩余寿命更接近实际值,证明了后验样本是先验样本的有力补充,对两者综合分析更能准确预测系统剩余寿命。
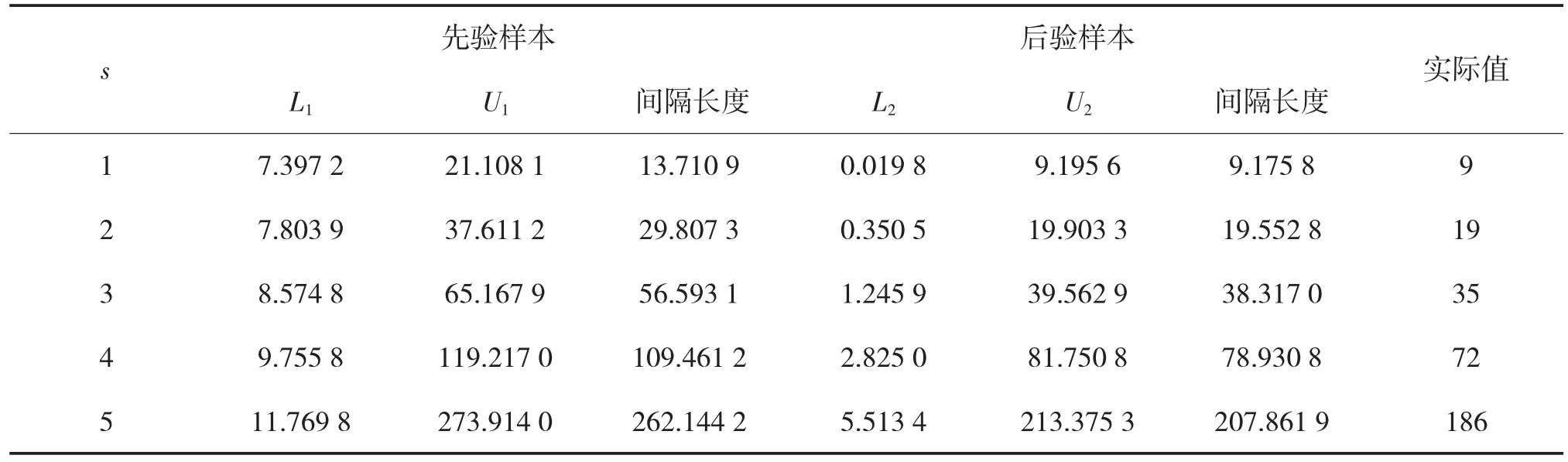
表2 预测结果与实际值对比
6 结论
相比指数分布,威布尔分布能更加真实地反映复杂系统的寿命特征,运用威布尔分布描述系统寿命时间,使得对系统剩余寿命的预测能够更加贴近实际,便于使用和维修人员安排合理的修理计划。本文运用极大似然方法和贝叶斯模型估计威布尔分布的两个未知参数,并给出这两个参数的贝叶斯置信区间,为威布尔分布在复杂系统剩余寿命预测中的应用打下基础。然后,在基于先验样本和后验样本的不同情况下,运用贝叶斯模型对该系统剩余寿命进行了预测研究。最后开展了实例分析,结果表明,该方法与实际试验结果更加接近,与传统基于先验样本的方法相比,该方法是有效的。
参考文献:
[1]杨志波,董明.动态贝叶斯网络在设备剩余寿命预测中的应用研究[J].计算机集成制造系统,2007,13(9):1811-1815.
[2]孙绍辉,王华伟,李伟.潜在故障期内航空发动机的剩余寿命预测[J].航空计算技术,2012,42(1):8-11.
[3]WANG W B.A two-stage prognosis model in condition based maintenance[J].European Journal of Operational Research,2007,12(182):1177-1187.
[4]NAGI G.Mark lawley residual life predictions from vibration-based degradation signals:a neural network approach a neural network approach[J].IEEE Transactions on Industrial Electronics,2004,51(3):694-700.
[5]YUEN H K,TSE S K. Parameters estimation for weibull distributed lifetimes under progressive censoring with random removals[J]. Statist Comput Simul,1996,3(55):57-71.
[6]FERNáNDEZ A J. On estimating exponential parameters with general type II progressive censoring[J]. Statist Plann Inference,2004,1(121):135-147.
[7]SOLIMAN A A. Estimation of parameters of life from progressively censored data using burr-XII model[J]. IEEE Trans Reliab,2005,5(54):34-42.
[8]ASGHARZADEH A. Point and interval estimation for a generalized logistic distribution under progressive type II censoring[J]. Commun Statist Theory Meth,2006,3(35):1685-1702.
[9]KUS C,KAYA M F. Estimation for the parameters of the pareto dsitribution under progressive censoring[J]. Commun Statist Theory Meth. 2007,2(36):1359-1365.
[10]MOUSA M A,SAGHEER S A. Bayesian prediction for progressively type-II censored data from the rayleigh model [J]. Commun Statist Theory Meth,2005,1(34):2353-2361.
[11]WU S J,CHEN D H,CHEN S T. Bayesian inference for rayleigh distribution under progressive censored sample[J]. Appl Stochast Models Bus Ind,2006,2(22):269-279.
[12]ELRAHMAN A M,SULTAN K S. Reliability estimation based on general progressive censored data from the Weibull model:Comparison between Bayesian and classical approaches[J]. METRON - Int Statist LXV,2007,6 (16):239-257.
[13]WU S J. Estimation of the two-parameter bathtub-shaped lifetime distribution with progressive censoring[J]. Appl Statist. 2008,3(35):1139-1150.
[14]KUNDU D. Bayesian inference and life testing plan for the weibull distribution in presence of progressive censoring[J]. Technometrics,2008,9(50):144-154.
[15]尹斌,郑先斌.武器装备全寿命管理中的标准化体系研究[J].四川兵工学报,2013,24(10):63-66.
[16]NELSON W. Applied life data analysis[M]. NewYork:Wiley Press,1982,3(176):514-532.
Bayesian Model for Predicting Residual Life of Equipment
LIU Gang1,2,LI Fang1,2
(1. Naval University. of Engineering,Wuhan 430033,China;2. Lab of Naval Vessel Integrated Logistics Support,Naval University. of Engineering,Wuhan 430033,China)
Abstract:To solve the problem of weapon equipment is the growing complexity and the maintenance work becoming heavy daily,the Bayesian model is applied to predicting residual life of equipment after repair,the foundation was proposed for reasonably arranging repair plan. The traditional exponential distribution is replaced,then Weibull distribution is used for describing life characteristic of system,furthermore,and the methods of Maximum likelihood and Bayesian are applied to estimating the two parameters of Weibull distribution,and the credible intervals are given. On the basis,according to the two situations that prior sample and posterior sample,the residual life after repair is predicted by Bayesian model respectively. The illustrative example is given in paper,and the proposed method is proved to be effective.
Key words:weibull distribution,bayesian,residual life,predict
中图分类号:TP391.73
文献标识码:A
文章编号:1002-0640(2016)05-0019-06
收稿日期:2015-04-05修回日期:2015-05-07
作者简介:刘刚(1982-),男,湖北武汉人,硕士,讲师。研究方向:装备综合保障工程、可靠性维修性测试性。

