鱼雷被动声自导搜索深度研究

由文立，周利辉，2，马宏岩

（1.海军潜艇学院，山东　青岛　266042；2.海军装备研究院，北京　100161）



鱼雷被动声自导搜索深度研究

由文立1，周利辉1，2，马宏岩1

（1.海军潜艇学院，山东青岛266042；2.海军装备研究院，北京100161）

摘要：鱼雷被动声自导搜索舰船时，设定深度的选择决定了搜索效能的发挥。被动自导方程各项中，鱼雷自噪声与传播损失随深度变化，二者在深度上的分布通过信号余量影响自导作用距离与检测概率。提出了基于被动自导平均检测概率的搜索效能值计算模型，将其作为鱼雷搜索深度选择依据。根据自噪声级、传播损失和声纳方程其他各项的仿真和计算，定量分析了3种典型声速梯度下搜索效能随深度变化情况，提出了被动声自导系统搜索深度设定原则。

关键词：鱼雷自导，搜索深度，自噪声，搜索效能值

0　引言

鱼雷被动声自导可单独使用，或与尾流自导相结合，用于打击中高速航行的大中型水面舰船。被动声自导系统在搜索目标时，水平弹道需要进行复杂的设计，而在垂直弹道上通常按照设定深度航行。鱼雷被动声自导系统本质上是一部小型声纳，其搜索深度的选择，决定了搜索效能的发挥。而设定深度如何选择，仅有部分定性分析和使用习惯，鲜有定量研究。

被动自导搜索深度的研究，前提条件是评价探测效果的准则或者指标，进而分析影响搜索效果的主要参量。自导作用距离是评价自导系统效能的主要指标，其计算主要依据自导方程，结合方程中各项参数的计算进行。被动自导方程各项参数中，鱼雷自噪声级和传播损失随深度变化。本文将综合考虑两方面的影响，提出一种新的更能准确反应被动自导效能的参数，作为鱼雷被动声自导搜索深度选择依据，研究不同水文条件下搜索深度设定原则。

1　鱼雷被动声自导搜索效能值计算模型

采用被动自导方程估算鱼雷自导作用距离时，通常以固定的检测概率（通常取0.5）确定检测阈，当声纳输出信噪比高于检测阈时则认为发现目标。该方法计算简单，但是并不能准确反映自导系统效能。在鱼雷自导方程的基础上，研究自导系统检测概率是一种可取的方法。在声纳检测概率方面，文献［1-2］采用随机声纳方程，以声纳方程中部分项的随机性研究声纳检测概率，进而进行声纳探测性能的预报。下面将从自导基阵和ROC曲线的角度研究自导系统检测概率及以之为基础的搜索效能值。

为了综合衡量各种因素的影响，采用基于声自导平均检测概率的搜索效能值作为评价鱼雷被动声自导深度选择的标准。采用离散方式计算，被动声自导搜索效能值定义为：

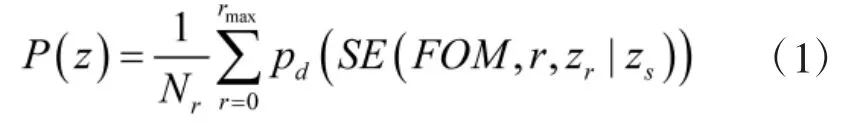
其中，P即检测概率pd在距离上的均值，r为雷目距离，Nr为水平方向计算点数，rmax为最大计算距离，SE为信号余量，FOM为声纳优质因子，zr和zs分别为鱼雷深度和目标深度。

检测概率pd是信号余量SE的函数，信号余量越大则检测概率越大。采用优质因子FOM与传播损失TL计算信号余量SE，当SE＞0时，则自导系统以某一概率发现目标。根据被动声自导方程，信号余量［3］为：

其中，Ra为经过自导系统波束形成后的信噪比，RT为信噪比门限，SL为声源级，TL为传播损失，NL为噪声级，AG为自导接收基阵阵列增益，DT为检测阈。被动自导方程各项中，传播损失TL与噪声级NL受自导系统工作深度影响。由于鱼雷自导工作频率较高，通常在15 kHz以上，采用高斯声线束（GRAB）模型计算传播损失TL。GRAB模型是高斯束动态声线跟踪算法的近似，但形式更加简单，适用于高频条件下本征声线和传播损失的快速计算，美海军标准的GRAB模型是CASS（Comprehensive Acoustic System Simulation）的子系统。

在高速航行时，鱼雷自导工作主要干扰为鱼雷螺旋桨空化噪声传播到基阵形成的自噪声。自噪声主要为体积散射自噪声NLV和界面散射自噪声NLS，采用文献［4-5］的计算方法，并对其模型进行修正，考虑自导系统接收波束角空间滤波对自噪声级的影响。

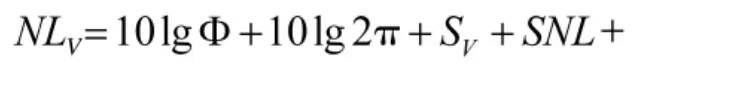
其中，SV为海水体积散射系数（通常为-90db～-70db），SNL（db）为鱼雷辐射噪声级，α（db/km）为海水吸收系数，r0（km）为自噪声仿真计算距离，H（m）为鱼雷距离海面或海底深度，Φ为被动自导系统接收指向性图，设鱼雷被动波束为理想波束情况，即立体波束角内的接收指向性为1，其余为0。

鱼雷被动自导搜索目标时，尚未发现目标，信号检测通常采用能量检测方式。若目标噪声信号幅值与环境噪声幅值均服从高斯分布，且被动自导系统为平方-积分处理方式，则自导接收机输出信号与噪声幅值服从瑞利分布。在宽带条件［4］下：

其中，pf为虚警概率，M为时间采样数，Δf为带宽（Hz），Δt为积分时间（s）。erfc为补偿误差函数，erfc-1为其反函数。

将pd转化为SE的函数。根据式（2）中SE的定义：

根据式（5）：

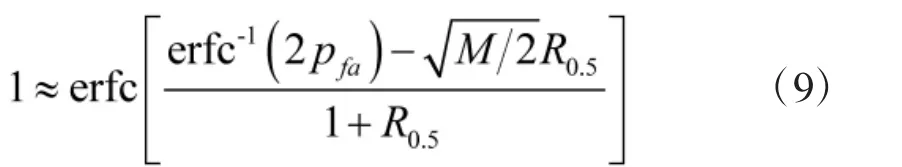
当信号余量SE＜0时，取pd=0。因此，检测概率

SE是将目标、环境和自导系统三者联系起来的量，采用基于信号余量的检测概率的平均作为自导系统搜索效能值，综合考虑了自噪声和传播损失对自导检测效能的影响。

2　鱼雷被动声自导搜索深度仿真分析

2.1鱼雷自噪声仿真分析

设海深100 m，海水吸收系数6 db/km，弱不平整海底，海底散射系数-18 db，海况三级，海面散射系数21 db，体积散射系数-80 db，鱼雷工作深度40 m，声自导水平波束角±35°，垂直波束角±10°，鱼雷辐射噪声级108 db，则在2 m～500 m的体积散射自噪声、海面散射自噪声、海底散射自噪声和鱼雷自噪声仿真结果如图1所示。

从图1可以看出，鱼雷自噪声主要是海底和海面散射产生，而体积散射自噪声可忽略。仿真距离超过15 m后，鱼雷自噪声趋于稳定。在鱼雷工作深度不同时，也具有类似结论。

为了研究鱼雷自噪声对被动自导搜索深度的影响，下面对鱼雷自噪声随深度变化进行分析。将鱼雷深度在5 m～95 m离散取值，自噪声仿真结果如图2所示。由图2可以看出，鱼雷在55 m、56 m深度航行时，自噪声最低，仅为55.81 db；鱼雷靠近海面或者海底时，由于界面散射的影响，自噪声较大，在5 m和95 m时，自噪声分别达58.9 db和57.9 db，超过55 m深度的自噪声为2 db～3 db，因此，有必要研究自噪声对鱼雷被动自导搜索深度的影响。

图1　鱼雷自噪声仿真分析结果

2.2鱼雷被动自导搜索效能值仿真与分析

设鱼雷被动自导工作频率为20 kHz，接收带宽1 kHz，采用GRAB模型［6］计算负梯度、正梯度和负跃层3种典型声速分布下的传播损失，如图3～图5所示。

图3为负梯度条件下的传播损失（图3（a））、信号余量（图3（b））、检测概率（图3（c）），图3（e）即为仿真分析得到的鱼雷被动自导在不同搜索深度上的搜索效能值。图3（c）可以看出，负梯度条件下，被动自导检测概率在45 m深度左右最大，超过0.9检测概率的自导作用距离约2.2 km。而在靠近海面和海底深度上，超过0.9检测概率的自导作用距离仅1.7 km左右。图3e可以看出，鱼雷被动自导最佳搜索深度为45 m，而图2的分析表明，在56 m深度最低鱼雷自噪声。这是由于负梯度条件下，声线往海底方向弯曲，使得大于声源深度上传播损失较小。鱼雷被动自导最佳搜索深度是综合考虑了鱼雷自噪声和传播损失在垂直方向上的分布的结果。

图2　鱼雷自噪声随深度变化情况

图3　负梯度条件下的被动自导搜索效能仿真

图4　正梯度条件下的被动自导搜索效能仿真

图4为正梯度条件下的传播损失、信号余量、检测概率和搜索效能值。图4（c）可以看出，正梯度条件下，被动自导检测概率在靠近海面的5 m深度最大，超过0.9检测概率的自导作用距离约2.9 km。而在靠近海底深度上，超过0.9检测概率的自导作用距离仅1.3 km左右。图3（e）可以看出，鱼雷被动自导最佳搜索深度为5 m。这是由于正梯度条件下，声线往海面方向弯曲，形成表面声道。传播损失成为影响被动自导搜索深度的主要因素。在鱼雷参数实际设定时，可设为接近海面的鱼雷航行上限深度。

图5为负跃层条件下的传播损失、信号余量、检测概率和搜索效能值。图5（c）可以看出，负跃层条件下，被动自导检测概率峰值59 m深度，超过0.9检测概率的自导作用距离约2.3 km。而在15 m左右的跃层深度上，超过0.9检测概率的自导作用距离仅1.6 km。图5（e）可以看出，鱼雷被动自导最佳搜索深度为59 m，同时在靠近海面的5 m深度上搜索效能仍比较理想。这是由于跃层中，传播损失较大，使得搜索效能值在跃层内存在波谷；在跃层以下，由于微弱正梯度和自噪声的共同影响，搜索效能值较高；跃层以上，由于鱼雷与目标处于跃层同一侧，

图5　负跃层条件下的被动自导搜索效能仿真

3　结论

仿真分析结果表明，在3种典型声速分布条件下，由于鱼雷自噪声和传播损失在水平深度上的差异，不同深度上的被动自导作用距离相差40%～50%，严重影响鱼雷被动自导搜索效果，进而影响鱼雷作战效能的发挥。在进行鱼雷搜索深度参数设定时，除了鱼雷航行深度限制、作战训练任务要求等约束，应综合考虑海况和海底地质为主要因素影响下的鱼雷自噪声，海区声速梯度条件影响下的传播损失在深度上的分布。本文的研究结果为鱼雷被动自导搜索深度的选择提供了依据和定量分析结果。

参考文献：

［1］笪良龙.海洋水声环境效应建模与应用［M］.北京：科学出版社，2012：143-151.

［2］陈建勇，鞠建波，冷江.吊放声纳被动探测的一次发现概率［J］.海军航空工程学院学报，2004，19（4）：482-484.

［3］AINSLIE M A.Principles of sonar performance modeling［M］. Berlin：Springer & Chichester：Praxis，2010：53-122.

［4］徐园园，王明洲，蒋继军.基于双基地模型的鱼雷自噪声仿真预报［J］.舰船科学技术，2012，34（12）：24-29.

［5］徐园园，王明洲，蒋继军.基于声散射模型的鱼雷自噪声特性分析及仿真预报［J］.鱼雷技术，2013，21（2）：105-109.

［6］赵宁.GRAB算法实现［D］.哈尔滨：哈尔滨工程大学，2008：19-28.

Research on Searching Depth of
Torpedo Passive Acoustic Homing System

YOU Wen-li1，ZHOU Li-hui1，2，MA Hong-yan1
（1.Navy Submarine Academy，Qingdao 266042，China；2.Naval Academy of Armament，Beijing 100161，China）

Abstract：Torpedo passive acoustic homing system searching efficiency depends on setting depth when detecting targets. Torpedo self-noise level and propagation loss of the passive homing equation change with depth，which impact on homing range and detecting probability through signal excess. Searching efficiency model is proposed to design torpedo working depth. The efficiency is calculated from mean detecting probability. Torpedo self-noise level，propagation loss and other parameters are simulated and calculated. Passive homing system searching efficiency changing with depth is analyzed under three typical SSP conditions. The principles of passive acoustic homing system detecting depth setting are put forward.

Key words：torpedo homing system，detecting depth，self-noise，searching efficiency

中图分类号：TJ63+1.5

文献标识码：A

文章编号：1002-0640（2016）05-0145-04

收稿日期：2015-04-05修回日期：2015-05-07

作者简介：由文立（1963-），男，辽宁沈阳人，硕士，高级工程师。研究方向：水中兵器使用与保障。