连续波强激光武器动态毁伤概率的非毁检测法*

王向民，王　军，郭　治

（南京理工大学自动化学院，南京　290014）



连续波强激光武器动态毁伤概率的非毁检测法*

王向民，王军，郭治

（南京理工大学自动化学院，南京290014）

摘要：给出一种强激光武器与目标存在相对运动时的毁伤概率（动态毁伤概率）在非致毁条件下的检测方法。该方法是在已知强激光对目标的致毁时间、一次发射时间的基础上，在武器的跟瞄子系统对目标无毁的跟踪试验中，通过检测跟踪误差在射击门内外交替出现的时间间隔，给出动态毁伤概率的点估计，以及在既定置信度下，动态毁伤概率的置信区间，同时还能判断所测毁伤概率是否处于最佳状态，为进一步优化动态毁伤概率提供依据。

关键词：强激光武器，性能评估，毁伤概率检测，非毁伤检测

0　引言

连续波强激光武器动态毁伤概率（以下简称毁伤概率）是指强激光武器与其射击对象存在相对运动时的毁伤概率。它是武器系统在作战时最重要的性能指标之一，因而也是该武器系统验收时最重要的检测指标之一。如果以射击过程中目标的毁伤数与发射次数之比来检测毁伤概率，那么要达到一定的测试精度，其毁伤目标的数目是验收工作难以接受的。为此必须寻找某种在对目标无毁伤条件下的毁伤概率的检测方法。为实现无毁检测，必须寻求毁伤概率的一种同毁伤现象没有直接关系的一组参数构建的毁伤概率数学模型，再通过对这组参数的检测结果，将毁伤概率计算出来。

本文引用的毁伤概率的数学模型来自文献［1］。之所以采用该模型，是因为该模型设定的目标致毁条件为当前已知的连续波强激光武器所遵循，而结论又是通过明晰的物理概念与严谨的数理逻辑推导而得，具有很好的普适性。

1　对被检测的强激光武器与检测设备的描述

记强激光束的束散角为2ρ，以待毁点O为中心，半径等于ρ的圆称为射击门，显然，跟踪误差Z（t）可能以不同的随机轨迹穿越射击门，如图1所示。

图1　射击门与跟踪误差的示意图

图中tin，i=｛t2i-1-t2i-1；i=1，2，…｝为辐照时间；而tout，i= ｛t2i-t2i-1；i=1，2，…｝为失照时间；tch，i=tin，i+tout，i=｛t2i+1-t2i-1；i=1，2，3，…｝为随机周期。很明显，tch，i，tin，i和tout，i都是随机变量。

若Z（t）=（x（t），y（t））T为相互独立、均方可导、各态历经、零均值的正态过程，强激光于t=t0瞬时发射，而在t-t0=Ts时结束。若在t∈［0，Ts］的时间内，存在一个n，使

则目标必被毁伤。当Th，Ts一定时，文献［1］以严谨的数学推理导出了它的毁伤概率

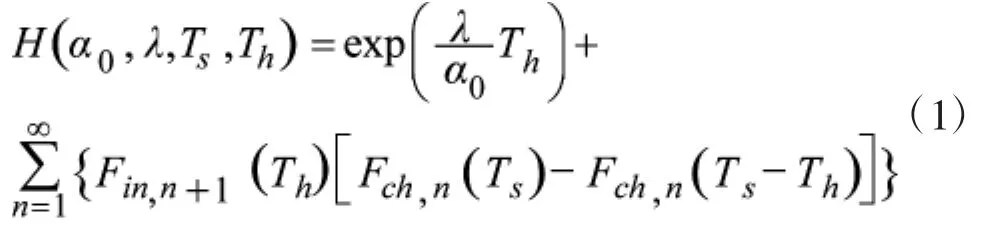
式中若α0=α1=0.5时，应以代入式（1）中进行计算。

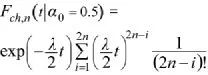
上述各式中：

α0=1-α1为跟踪误差Z（t）在射击门内的概率为Z（t）穿入射击门的平均频率。

本文的主要任务就是给出通过实测的Tin与，检测出α0和，再通过式（1）给出毁伤概率的检测值。

2　毁伤概率的点估计

由于单个辐照时间tin，i的密度函数服从以参数为的指数分布［2］

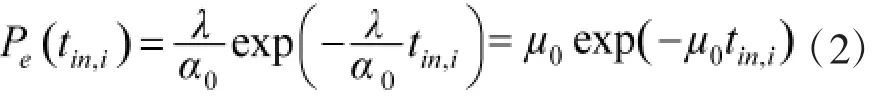
可得μ0最大似然估计［3］

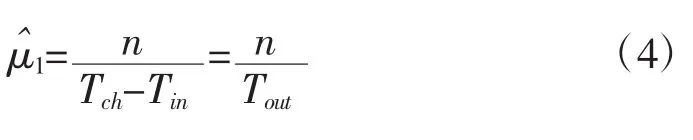
考虑到

故有

从而有

而

3　参数α0　与?估计的上下界

对n个辐照时间之和Tin而言，其密度函数［1］

则χ2的密度函数

为自变量为2μ0Tin=χ2、自由度为2n的χ2分布。

若给定置信度1-α，则有

在上述置信度下

显然，上述置信度区间的上限和下限，当n一定时，仅与对应的总辐照时间有关。

在与上述相同的置信度下，μ1的置信区间为

考虑到式（4）则有

与

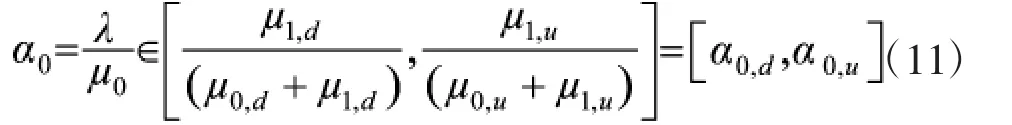
4　毁伤概率的置信区间估计

分别以α0，d，α0，u为已知参数，利用式（1）计算不同∈［d，u］下的毁伤概率，可得下述两条毁伤概率曲线H（，α0，d）和H（，α0，u），如图2所示。分别找出毁伤概率曲线在∈［d，u］可能存在的极小值点（'d，α0，）d，（'u，α0，）u与极大值点（''d，α0，）d，（''u，α0，）u。由于毁伤概率的置信区间应该是∈［d，u］内上述两条毁伤概率曲线的最大间隔，如果'd，'u，''d，''u出现在区间［d，u］之内，它们也可能因取该区间内最大间隔，而成为置信区间，如图2所示。故有

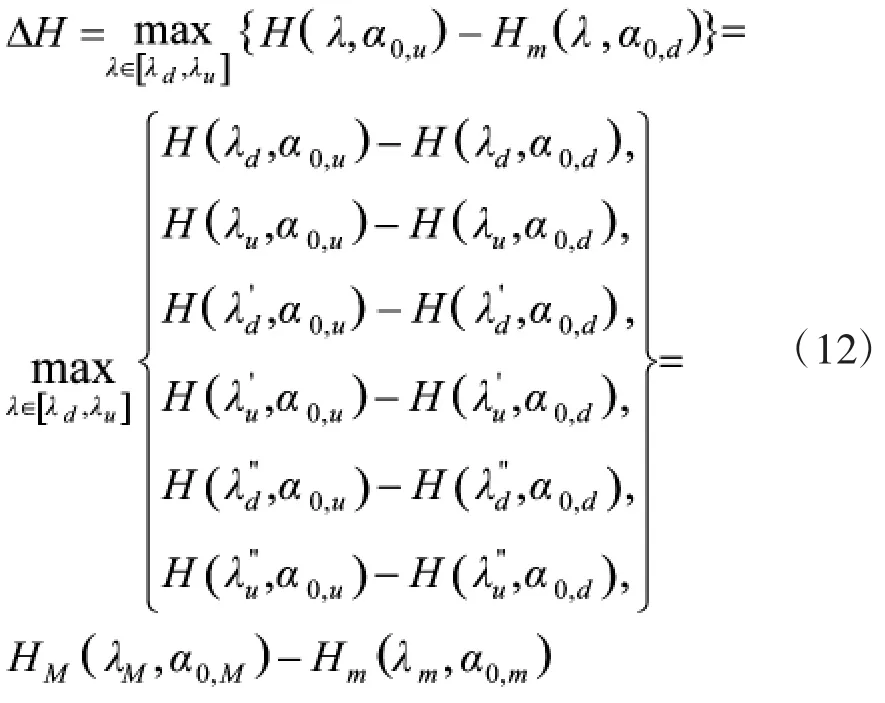
从而得毁伤概率置信区间

注意：在式（7）中，直接以毁伤概率的置信度1-α作为2μ0Tin的置信度，这种代替可能导致毁伤概率置信度的误差。如果这个误差较大，应予以修正。

5　关于毁伤概率的置信度的修正

常规的置信区间的论证都在给出毁伤概率的置信度的基础上推导。这种要求，对本文的命题而言难以做到。然而，成功的完成本文给出的检测后，却可以通过检验其相应的毁伤概率的置信度。其具体做法是：在检测了n个随机周期中找到最小的辐照时间T'in（1）与失照时间T'out（1），以及最大的辐照时间T''in（1）和失照时间T''out（1），再将上述各值代入式（7）中，得

与

当以上述参数为值，计算出α0，与的区间后，并进一步计算，即可得一个毁伤概率的置信区间，该区间的宽度为△H（1），则毁伤概率的置信度即为1-α*=1-△H（1）。

倘若认为上述反推出来的α*过大，可以减小式（7）中的2μ0Tin置信度α，重新测试置信区间，直到它满足要求后，再以此时已累积的所有随机周期中找出最小与最大的单个辐照与失照时间，得出一个新的置信度1-α*。如它仍不符合既定要求，再继续测试，到满足要求为止。此时，随机周期的总数n即可作为此型号检测方案中必须检测的随机周期数。

由于实际激光跟踪误差的随机周期的均值都在秒的数量级上，记录千百个随机周期的试验时间一般均能接受，而且跟踪误差的检测成本低廉，因而，于正式检验之前，先以试验方法给出毁伤概率在既定置信度下具有给定置信区间的试验次数，以应用于正式检验与后续检验，不仅降低了检测的风险，而且是可行的。

6　毁伤概率的检测步骤

检测方案要求在已知强激光的致毁时间Th与一次发射时间Ts的条件下，通过对检测目标跟踪误差对射击门随机穿越的随机的时间间隔来实施。由于不要求发射强激光，故建议检测时间以对目标的一次典型的跟踪时间T为单位，逐次实施。其步骤如下：

①记录并提取一次跟踪时间［0，T］内的全部辐照时间Ti（nn）与全部失照时间Tou（tn）；

⑤依据式（12）、式（13）求出毁伤概率置信区间［H（dn），H（un）］；

⑥若H（un）-H（dn）＞△H，则继续进行下一次跟踪试验，将测得的

加入前一次结果之中，即

n+n'⇒n

重复步骤②～步骤⑥，直到Hu-Hd≤△H为止。

⑦提取累次检测时间内最小的辐照时间T'in（1）与失照时间To'u（t1），以及最大的辐照时间Ti'n（'1）和失照时间T'o'u（t1），依式（14）、式（15）计算出［μ0，（d1），μ0，（u1）］，［μ1，（d1），μ1，（u1）］，重复步骤③～步骤⑥，可得H（1）∈［H（1）d，H（1）u］，即毁伤概率的置信度为1-α*=1-△H（1）。如果认为过大或过小，可通过增加或减少试验次数，再继续重复本步骤的测试过程，直到其满足要求为止。

⑧若已知强激光武器待检的毁伤概率为H，当H∈［Hd，Hu］时，接受为合格值，否则拒绝。

7　检测示例

已知强激光武器的致毁时间Th=2.5 s、一次发射时间Ts=4 s，强激光在目标上的半束散角为ρ=1.5。用Matlab工具箱生成各态历经的、零均值正态序列Z（k），模拟激光方向跟踪误差Z（t）。

要求给出上述被模拟的强激光武器在置信度1-α=0.9，置信区间△H=0.05条件下的毁伤概率的检测方法。

首先依据实际可跟踪目标的时间，确定跟踪时间T，通常T≥10Ts，本例选择T=100 s左右，得到第一条跟踪误差函数（数据从略）；检测出辐照时间与失照时间序列Tin，i，Tout，i，i=1，2，…，n；取1-α=0.9，依前述检测步骤，得到检测结果如表1所示。

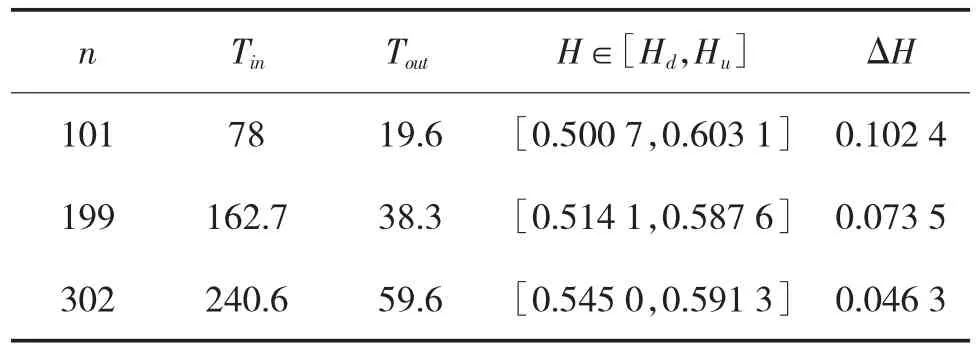
表1　检测结果表

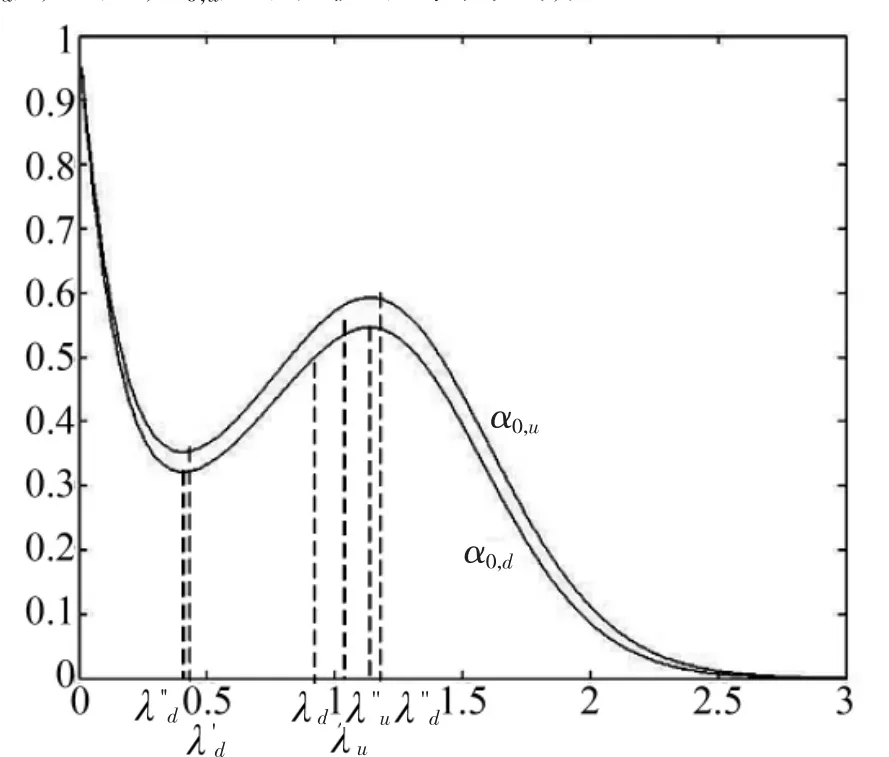
图2　α0，d，α0，u的毁伤概率曲线。

如对式（7）的近似用1-α=0.9作为毁伤概率置信度不能接受，可反推上述检测所对应的α的估值。即在已测得的n=302个随机周期中选取最小、最大辐照时间和失照时间，本例中Ti'n（1）=0.5s，To'u（t1）= 0.1 s，T'in（ '1）=3 s，T'o'u（t1）=0.5 s；代入式（13）、式（14），得到［μ0，（d1），μ0，（u1）］与［μ1，（d1），μ1，（u1）］；再依次检测步骤⑤、步骤⑥，即可得相应的置信区间H（1）∈［0.911 3，0.979 6］，故有1-=1-△H（1）=0.931 7＞0.9=1-α。这表明以检测n=302个随机周期的试验数据给出的毁伤概率的估值=0.546 7在比0.9更高的置信度下，具有的误差小于0.05，更应该接受。

参考文献：

［1］王向民，王军，郭治.连续波强激光武器动态毁伤概率的数学模型［J］.火力与指挥控制，2016，41（2）：55-59.

［2］朱位秋.随机振动［M］.北京：科学出版社，1992.

［3］陈萍.概率与统计［M］.北京：科学出版社，2002.

Test Method for Dynamic Damage Probability of the CW High- energy Laser Devices Without Damage

WANG Xiang-min，WANG Jun，GUO Zhi
（School of Automation，Nanjing University of Science and Technology，Nanjing 210094，China）

Abstract：The test method of the damage probability（dynamic damage probability）of the CW high-energy laser devices without damage is presented when there is a relative movement between the devices and the target. On the basis of the known the damage time and the length of a launch time of the devices，the method detects the alternately appear time interval of the tracking error in shooting door internally and externally in the tracking experiments，gives the point estimation of the dynamic damage probability，and the confidence interval under the known confidence level is given. Meanwhile，it can judge the damage probability will be in the best possible condition，which offers technological support on optimizing the dynamic damage probability.

Key words：CW high power laser，performance evaluation，damage probability testing，non-damage testing

中图分类号：TP273；TJ95

文献标识码：A

文章编号：1002-0640（2016）05-0121-04

收稿日期：2015-03-10修回日期：2015-04-11

*基金项目：国家自然科学基金项目（61104197）；国家部委预研基金资助项目（40405070103）

作者简介：王向民（1975-），男，湖南南华容人，博士，助理研究员。研究方向：火力控制。