一种用于战场态势分析的决策支持方法
岳东峰,高甜容,王殷辉,许 畅,张 玲
(北方信息控制集团有限公司,南京 211153)
一种用于战场态势分析的决策支持方法
岳东峰,高甜容,王殷辉,许畅,张玲
(北方信息控制集团有限公司,南京211153)
摘要:针对战场态势分析过程中存在的关键情报缺失问题,在离散事件系统的模型基础上,总结已有决策支持方法并加以改进,提出一种步进融合算法,构建出新的决策支持系统。采用数学手段及实例验证对所提出方法与已有方法进行性能比较,证明该方法能够有效保证指挥决策的鲁棒性和敏捷性,适用于战场态势分析。
关键词:决策支持,辅助决策,态势分析,离散事件系统
0 引言
随着信息技术和高精尖武器的飞速发展,现代战争逐渐演变为快吃慢的战争格局,战场态势瞬息万变,因此,指挥决策人员需要在极短的时间内针对当前战场态势作出快速反应。此外,随着战争迷雾的不断加剧,很多会导致战场态势变化的关键情报真假难辨,甚至无法获取,造成当前态势不明,影响指挥决策人员的判断和行为。因此,本文提出一种快速的决策支持方法对当前情报进行分析,判断当前态势,进而辅助指挥决策人员制定作战计划。
离散事件系统(Discrete Event System,DES)由于其简单、快捷、普适的特性,往往被用于有向态势图的建立和态势分析[1-3]。本文在DES的基础上,对战场态势的演变过程进行建模,根据态势演变过程中情报不易获取的特性,引入Antonia[4]等人的算法模型进行态势分析,并针对该模型在分析过程中产生的复杂性、时效性等问题,提出了一种新的决策支持方法。
1 基于DES的决策支持方法
1.1战场态势的经典G模型表示
战场态势的演变过程可由经典DES G模型进行表示,如下页图1所示,其中xi为不同的战场态势,ei为导致战场态势演变的关键事件。
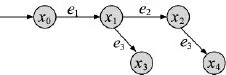
图1 战场态势的经典DES G模型表示
经典DES G模型可由五元组表示,G=(X,E,f, Γ,x0),以图1为例,其中:X为态势集合,X={x0,x1,x2,x3,x4}。x0为初始态势,x0∈X。E为事件集合,导致态势演变的关键事件,E={e1,e2,e3}。f为态势迁移函数,f(x,e)=xe表示若战场处于态势x时发生事件e,则战场态势迁移为xe。f(x0,e1)=x1,f(x1,e2)=x2,f(x1,e3)=x3,f(x2,e3)=x4。Γ为态势事件函数,Γ(x)表示战场处于态势x时会导致态势发生改变的关键事件的集合。Γ(x0)={e1},Γ(x1)={e2,e3},Γ(x2)={e3},Γ(x3)=Ф,Γ(x4)=Ф。
假设e1事件为我军推进到A阵线,e2事件为我军推进到B阵线,e3事件为我军占领高地T,则图1所示模型的含义为:
(1)战场初始态势为x0;
(2)当我军推进到阵线A时,战场态势变为x1;
(3)在x1态势,当我军推进到阵线B时,战场态势变为x2;
(4)在x1态势,当我军占领高地T时,战场态势变为x3;
(5)在x2态势,当我军占领高地T时,战场态势变为x4。
(6)态势x3和x4的区别在于,高地占领时机的不同会导致我军部队在阵线推进过程中伤亡数量的不同,从而影响态势。
经典DES G模型虽然可以表示战场态势随事件发生的演变过程,但却无法提供有效的决策支持,尤其是随着信息化技术的飞速发展,现代战争中情报迷雾重重,有些关键事件的情报获取极其困难,或者真假难辨、不可使用。因此,笔者在工程实践中引入Antonia[4]等人提出的GPP模型并加以适应性修正,以解决上述问题。
1.2战场态势的GPP模型表示
战场态势的GPP模型表示如图2所示,其中xd为不利态势,es为无法获取相关情报的关键事件。该模型的应用目的在于,充分考虑事件的缺失性,对战场态势的演化模型进行重新建模和分析,从而寻找会导致不利态势发生的关键事件,并给出决策支持,辅助指挥者全力阻止该事件的发生。

图2 战场态势的GPP模型初始表示
GPP模型可使用六元组进行表示,GPP=(XPP,EPP,fPP,ΓPP,x0,PP,XD,PP),其中:XPP为态势集合。x0,PP为初始态势,x0,PP∈XPP。XD,PP为不利态势集合,X={xd}。EPP为事件集合,导致态势演变的关键事件。EPP=Eo,PP∪Euo,PP,其中Eo,PP表示可以获取的事件,而Euo,PP则表示无法获取的事件,Eo,PP∩Euo,PP=Ф。fPP为态势迁移函数,fPP(x,e)=xe表示若战场处于态势x时发生事件e,则战场态势迁移为xe。ΓPP为态势事件函数,ΓPP(x)表示战场处于态势x时会导致态势发生改变的关键事件的集合。
由于经典G模型在描述战场态势的过程中,是基于全部事件均可获取假设的基础上的,因此,GPP模型延续了这种前提假设,仍然认为es事件是可以获取的,在此基础上引入两个新事件ef0和es’,其中ef0表示es事件的获取渠道被摧毁的事件;es’表示在无法察觉的情况下,es事件的发生。
因此,图2所示有向态势图被GPP模型转换为图3所示状态。

图3 战场态势的GPP模型演化
GPP模型同经典G模型之间的关联关系可描述如下:

由于无法获取关键事件的存在,无法准确判断战场态势具体处于何种状态,因此,GPP模型算法将可能的战场态势进行合并和裁剪,并最终得到新的战场态势有向图,如下页图4所示。具体演化过程请参考文献[4],本文不再赘述。
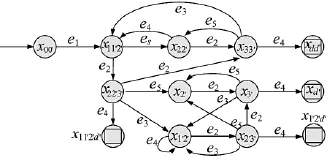
图4 战场态势的GPP模型表示
GPP模型虽然能够适用于情报缺失的战场态势分析和决策支持,但复杂度高,仅针对一个事件缺失的情况,ef0的引入便使得系统的状态数产生了近两倍的扩充,如若有多个事件缺失,则GPP模型所产生的状态数会变为原系统状态数的2n倍,严重影响后续合并和裁剪过程的复杂度与处理时间。
2 改进的决策支持方法
为有效解决GPP模型存在的上述问题,本文提出一种新的决策支持模型GSF模型,并在此基础上采用步进融合算法,对态势状态进行合并和裁剪,从而降低复杂度,加快态势分析处理的时间。
2.1GSF模型
GSF模型也使用六元组进行表示:GSF=(XSF,ESF,fSF,ΓSF,x0,SF,XD,SF),同GPP模型的区别在于GSF模型不再引入新的事件,而是对es事件进行特殊处理,将其所属事件类型定义为Es,该类型的事件既作为可获取的事件对待,也作为不可获取的事件对待,在进行状态合并和裁剪过程中,根据双重贪心策略将Es在Eo和Euo之间进行切换。
GSF模型同经典G模型之间的关联关系可描述如下:

其中,为方便语言描述,本文采用以下常用标识和函数:Q为GSF模型中的状态元素,为G模型中部分状态的集合,如Q0={x0},Q1={x1,x2};UR为态势合并函数,UR(x)={y∈X:(∃t∈Euo*)[f(x,t)=y]},表示当战场处于态势x时,由于无法获取的关键事件的发生,导致战场进入的所有可能态势状态的集合。L(G)表示G模型中的所有事件发生顺序,如{e1,e2,e3}⊆L(G)⊆E*。
2.2步进融合算法
本文所设计步进融合算法使用双重贪心策略,在进行状态融合时将Es类型事件作为无法获取的事件进行处理,而在进行状态迁移时作为可获取的事件进行处理,从而实现新生状态集合与其上关键事件的最大集,增强战场态势演变的自由度。
步进融合算法的伪代码描述如下,其基本思想是,从G系统初始状态x0开始建模,针对当前状态可能发生的所有事件,建立态势迁移函数,同时对所迁移至的态势状态考虑其后继事件,根据态势合并函数,将所有Eo类型事件以及Es类型事件所导致的态势状态进行融合,形成新的状态集合。重复上述步骤,直到出现不利态势状态或没有新的态势状态出现为止。

其中:XSF,ing为正在构建中的态势状态集合,该集合中的态势状态已针对Eo类型事件以及Es类型事件完成了状态合并,但还未曾定义态势迁移函数fSF;XSF为已构建成功的态势状态集合;URSF为重新定义的态势合并函数,URSF(Q)={x∈X:[∃e∈(Euo∪Es)*][f(q,e)=x],q∈Q},表示当战场处于态势Q时,由于Euo类型事件以及Es类型事件的发生,导致战场进入的所有可能态势的集合;ΓSF为重新定义的态势事件函数,ΓSF(Q)=∪x∈QΓ(x),表示战场处于态势Q时可能发生的所有会导致态势迁移的事件集合。
2.3应用示例
GSF模型对图2所示战场态势的演化过程如图5所示,同图4相比,结果图更为简单和清晰。


图5 战场态势的GSF模型演化过程示例
3 性能分析
DES模型的评估标准一般为演化自由度、结果复杂度以及模型生成时间[5-12]。本文根据上述3种评判标准对所提出的GSF模型和GPP模型进行性能对比。
3.1演化自由度
由于指挥决策人员的精力和可投入兵力的有限性,所设计的决策支持系统应当最大限度允许事件的发生和战场态势的迁移,仅针对最关键的事件对指挥员进行提醒和决策支持,而演化自由度便是用于评价该能力的指标。
本节以两个定理对该性能进行论证,其中,定理1证明本文所设计的GSF模型在根本上仍然是典型的G模型,这是定理2论证的基础;定理2证明本文所设计的GSF模型同GPP模型相比,允许更多事件的发生,并且不会导致不利态势的出现,亦即对关键事件的识别更准确,对指挥决策人员的干扰更少,从而证明GSF模型在态势迁移自由度上的优越性。
定理1. Es=Ф⇒L(GSF)=L(G)证明:Es=Ф
⇒Eo,SF=Eo,Euo,SF=Euo,
URSF(Q)={x∈X:[∃t∈(Euo∪Ф)*][f(q,t)=x],q∈Q}=UR(Q),
fSF(Q,e)=UR[∪q∈Qf(q,e)]=f(Q,e)
又∵x0,SF=UR(x0)=x0
⇒GSF=G
定理2. L(GPP)⊆L(GSF)
证明:以上定理等同于证明下述假设不成立:
∃l∈L(GPP),但l∉L(GSF)
考虑到空语言ε∈L(G),等同于证明下式不成立,其中,t为事件语言,σ为单个事件:
∃tσ∈L(GPP),使得t∈L(GSF),而tσ∉L(GSF)
∵GPP⊆GSF
∴在GPP模型中经过语言t能够到达的状态,在GSF中同样能够到达。
⇒fPP(x0,PP,t)⊆fSF(x0,SF,t)
又∵tσ∈L(GPP)
而且ef0ues∉L(GPP)
∴ef0ues∉tσ
如果σ=es
⇒ef0∉t
⇒Es=Ф
⇒L(GSF)=L(G)=L(GPP)
又∵tσ∈L(GPP)
∴tσ∈L(GSF)
同上述假设矛盾。
∴es∉tσ
又∵ΓPP(fPP(x0,PP,t))=ΓSF(fSF(x0,SF,t)){es}
而σ∈ΓPP(fPP(x0,PP,t))
∴σ∈ΓSF(fSF(x0,SF,t))
∴tσ∈L(GSF)
也同上述假设矛盾。
所以,下述命题不成立:
∃tσ∈L(GPP),使得t∈L(GSF),而tσ∉L(GSF)
亦即L(GPP)⊆L(GSF)得证。
3.2结果复杂度
本节以文献[14]中的10个DES系统为原型,模拟战场态势迁移情况,并随机挑选3个事件作为无法获取确切情报的事件,分别对GPP和GSF模型算法展开对比研究,这10个DES系统如图6所示。

图6 战场态势迁移模拟实验图
实验过程中,为测试Es类型事件(缺失的情报)的数量对两种模型的影响程度,分别进行了3组实验,第1组实验中,设定eS0事件无法获取;第2组实验中,设定eS0事件和eS1事件无法获取;第3组实验中,设定eS0事件、eS1事件和eS2事件无法获取。
3组实验所得状态结果复杂度如图7和图8所示,实验结果表明:
(1)GSF模型所得结果状态数普遍低于G模型状态数量。这是因为针对无法获取的事件,GSF算法在生成新的模型过程中存在状态融合过程和剪枝过程,能够在一定程度上降低状态数量。
(2)GPP模型所得状态数普遍高于G状态数量。这是因为GPP模型在构建之初便根据Es事件的数量进行了扩充,所以虽然后续也存在一定的融合和剪枝过程,但仍然无法有效减少最终的状态数。
(3)随着Es事件数量的增多,GSF模型所得结果状态数波动较小,GPP模型所得结果状态数波动较大,存在明显的上升趋势。这是因为GPP模型所得结果状态数会随着Es事件数量的增多呈指数级增长,而GSF模型中的步进融合算法受此影响较小。
(4)GSF模型所得结果事件数普遍略高于G模型事件数量。这是因为GSF模型在步进融合过程中,针对每一个融合生成的新状态,都对其可能发生的事件采用了并操作,因此,GSF模型中每个状态的事件集普遍高于G模型,同时由于GSF模型中状态数量降低的程度并不大,所以GSF模型所得结果事件数普遍高于G模型事件数量,但增长幅度并不明显。
(5)GPP模型所得结果事件数普遍高于G模型事件数量和GSF模型事件数量。这是因为GPP模型中的状态数量过多,而且每个状态的事件集大小并未得到有效控制,所以导致了GPP模型中事件数量的增多。
(6)随着Es事件数量的增多,GSF模型结果事件数受波动较小,GPP模型结果事件数受波动较大。这是因为GSF模型中的步进融合算法受Es事件数量的影响较小,而GPP模型所得结果状态数会随着Es事件数量的增长呈指数级上升,因此,GPP模型所得结果事件数量会呈爆炸性增长。
综上所述,GSF模型无论是在结果状态数量方面,还是结果事件数量方面,还是在受Es事件数量的影响方面,均优于GPP模型[7]。

图7 GPP与GSF模型结果状态数比较图
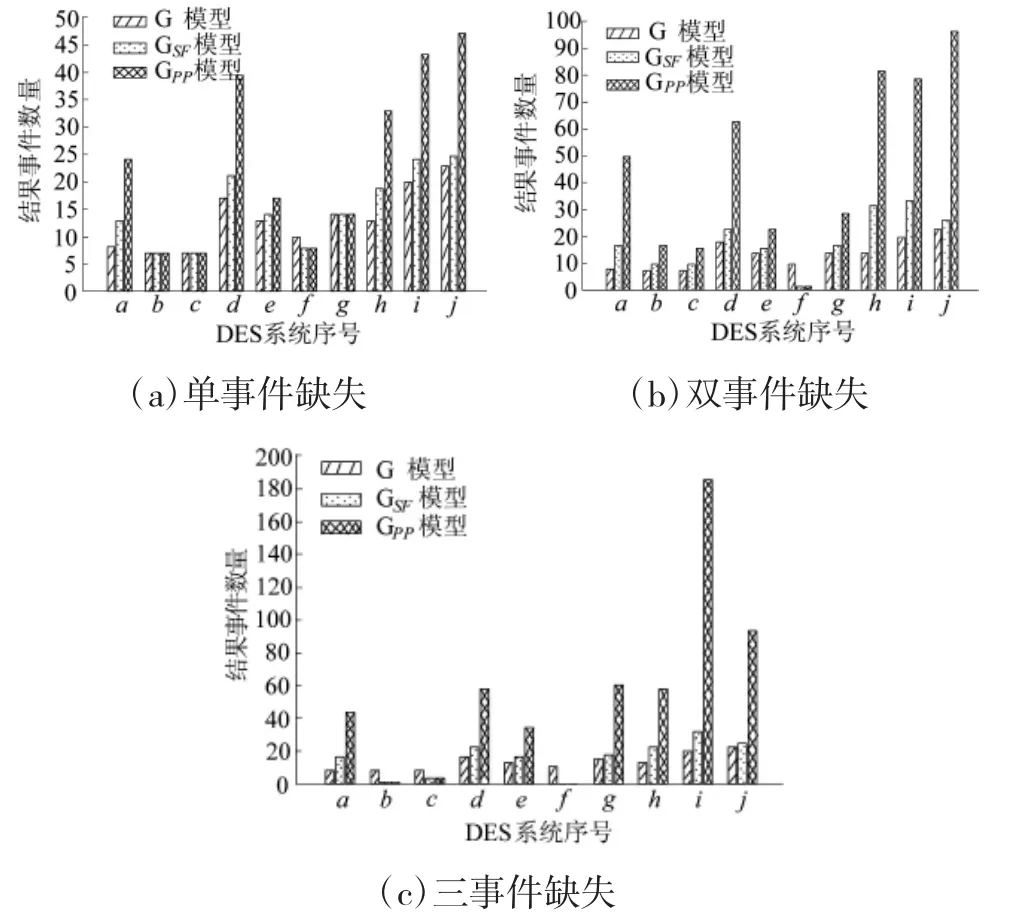
图8 GPP与GSF模型结果事件数比较图
3.3模型生成时间
上节分别针对10个DES系统进行了3组实验,共计30次实验,在实验过程中,本文对每次实验的运行时间进行了记录,结果如图9和图10所示。
实验所用编程语言为C++ 6.0,硬件环境为2.20 GHz Intel Pentium Dual E2200 CPU双核处理器,1.99 GB内存。
图9中是30次实验中两种模型的生成时间对比,前十次实验是eS0事件缺失的情况,中间十次实验是eS0事件和eS1事件缺失的情况,后十次实验是eS0事件、eS1事件和eS2事件缺失的情况。
图10是分别显示GSF模型和GPP模型的生成时间内部比较图,以说明两种模型在执行时间上受Es事件数量的影响程度。
从图9和图10的实验结果中可以得知:
(1)GSF模型生成时间均在3 ms以内,远低于GPP模型,具有良好的时间性能;而且随着Es事件数量的增长,GSF模型与GPP模型在时间上的差距越来越明显。
(2)在Es事件数量相同的情况下,GSF模型相比于GPP模型而言,在生成时间的性能上,受DES系统初始结构的影响较小,基本没有波动;而GPP模型受影响较大,各DES系统的演化时间快慢不一。
(3)对于同一个DES系统,GSF模型生成时间受Es事件数量影响较小,最大波动未超过1.5 ms;而GPP模型生成时间受影响较大,波动较为明显,最大波动已超过80 ms。
综上所述,GSF模型在生成时间方面受DES系统初始结构和Es事件数量的影响较小,优于GPP模型。
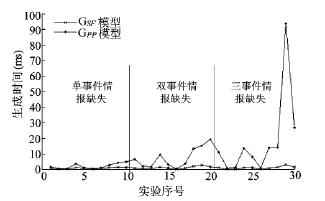
图9 GPP与GSF模型生成时间比较图

图10 GPP与GSF模型生成时间内部比较图
4 结论
本文在离散事件系统的基础上,提出了一种基于步进融合算法的决策支持方法,具有更低的算法复杂度和更快的决策反应时间,能够很好地用于对关键事件的发觉与处理决策支持,适用于现代战争迷雾下的态势分析。
后续研究将从以下方面深入展开:
(1)目前的决策支持方法主要用于防止不利态势的发生,后续将开展对有利态势促进决策的研究。
(2)有些关键事件的发生是无法阻止的,如敌方兵力的规模扩充等,因此,辅助决策应保证在事件可控的范围内进行,后续将开展相关研究。
(3)针对大量的战场态势和事件情报信息,将开展以大数据和云计算为基础的决策支持方法,在任务划分、并行计算等技术方向展开研究。
参考文献:
[1]武云鹏.鲁棒性军事行动过程方案生成与优化方法研究[D].长沙:国防科学技术大学,2012.
[2]张琳,陈绍顺.基于集对分析的战场态势分析模型[J].情报指挥控制系统与仿真技术,2005,27(5):55-59.
[3]李志强,胡晓峰,司光亚,等.基于人工势场的军事态势分析模型[J].火力与指挥控制,2007,32(4):5-8,11.
[4]SANCHEZ A M,MONTOYA F J. Safe supervisory control under observability failure[J]. Discrete Event Dynamic Systems,2006,16(4):493-525.
[5]RAMADGE P J,WONHAM W M. Supervisory control of a class of discrete event processes[J]. SIAM Jounal of Control and Optimization,1987,25(1):206-230.
[6]舒少龙,林峰,黄志强.离散事件系统的可测性[J].计算机工程与应用,2007,43(15):19-21.
[7]彭汉国,马良,杨伟,等.基于协同作战信息质量的战场态势认识模型[J].四川兵工学报,2013,24(11):99-102.
[8]YOUNG S,GARG V K. Model uncertainty in discrete event systems[J]. SIAM Journal of Control and Optimization,1995,33(1):208-226.
[9]LIN F. Robust and adaptive supervisory control of discrete event systems[J]. IEEE Transactions on Automatic Control,1993,38(12):1848-1852.
[10]SAMPATH M,SENGUPTA R,LAFORTUNE S,et al. Diagnosability of discrete event systems[J]. IEEE Transactions on Automatic Control,1995,40(9):1555-1575.
[11]CONTANT O,LAFORTUNE S,TENEKETZIS D. Diagnosability of discrete event systems with modular structure[J]. Discrete Event Dynamic Systems,2006,16(1):9-37.
[12]WANG Y,YOO T S,LAFORTUNE S. Diagnosis of discrete event systems using decentralized archi(ectures[J]. Discrete Event Dynamic Systems,2007,17(2):233-263.
[13]BOEL R. Adaptive supervisory control[M]. Norwell:Synthesis and Control of Discrete Event Systems,2002:115-123.
[14]CASSANDRAS C G,LAFORTUNE S. Introduction to discrete event systems[M]. New York:Springer Science + Business Media,2008.
A Decision Support Method for Battle- field Situation Analysis
YUE Dong-feng,GAO Tian-rong,WANG Yin-hui,XU Chang,ZHANG Ling
(North Information Control Group Corporation Limited,Nanjing 211153,China)
Abstract:To solve the problem of battle -field situation analysis under possible loss of observability of important information,a step -fusion algorithm which considering the repair of observability failure is proposed,and traditional methods which are used for Discrete Event System (DES)are described in detail. Based on the step-fusion algorithm,a new decision support method is presented. And then mathematic methods and case studies are adopted to compare the performance between the new and traditional mechanisms. The results proved that the new mechanism can obtain a robust system for battle -field situation analysis,and be lower complexity than the traditional supervisor.
Key words:decision support,assistant decision-making,situation analysis,DES
中图分类号:TP13
文献标识码:A
文章编号:1002-0640(2016)05-0100-07
收稿日期:2015-04-05修回日期:2015-04-27
作者简介:岳东峰(1984-),男,河北衡水人,博士。研究方向:自主决策系统,大数据处理系统。

