基于改进信息熵的抢修操作过程复杂性测度模型

尤志锋，李　震，胡起伟，田　霞

（军械工程学院，石家庄　050003）



基于改进信息熵的抢修操作过程复杂性测度模型

尤志锋，李震，胡起伟，田霞

（军械工程学院，石家庄050003）

摘要：抢修操作过程复杂性既是抢修人员准确衡量抢修操作难易程度及不确定性的重要指标，又是辅助指挥员进行抢修任务分配及抢修资源调度的重要参考，还是进行抢修时间估计的重要依据。然而，目前没有合适的抢修操作过程复杂性测度方法。考虑到普通信息熵极大值公理与抢修操作过程复杂性的特征不相符，利用改进的信息熵建立抢修操作过程的复杂性测度模型，并利用回归分析法通过实例验证，模型测度结果可以客观地反映抢修操作过程的复杂性。

关键词：抢修操作过程，复杂性测度，改进信息熵，难度系数，回归分析

0　引言

抢修操作的实施过程是以抢修方案为基础对具体损伤装备（一个或多个）进行抢修操作的过程；是一个利用现有资源，按照抢修设计的流程，使损伤装备恢复到规定功能的工艺操作过程；是将抢修方案、抢修方法付诸于实施的具体过程。损伤评估决策是前提条件，而抢修操作是将“前提”转化为现实的“工具集”。没有抢修操作过程，再好的决策也起不到丝毫作用［1］。因此，分析探讨抢修操作实施过程的复杂性及其测度，是抢修活动复杂性研究过程中的一项重要内容。从类型上看，抢修操作实施过程属于过程的一种。过程的复杂性分析在制造领域和软件工程领域被广泛研究和应用，并取得了较好的效果［2-4］。

目前为止，没有统一的复杂性定义，在不同的领域有不同的结论。这里借鉴软件复杂性与项目复杂性的定义［4-5］，将抢修操作过程复杂性定义为：在当前条件下，利用现有资源完成抢修操作过程的难度与不确定性的总称。它是复杂性在具体领域的微观运用，是难度的一种扩展。“抢修操作过程复杂性”包括完成抢修操作过程所采用的工具、方法、知识技能及人员等，是完成时间、出错率、工作量等指标的抽象。

熵是典型的不确定性度量的方法，其中又以信息熵最为常用。信息熵可以用来进行评估，其应用主要有两种思路，一种思路是用指标值反应出的信息量的多少作为权重确定的依据，即熵权法，然后利用加权综合法进行评估［6］；另一种是利用信息熵是度量信息量多少的本质，直接用描述一个系统、事件所需的信息量进行评估［7］。根据抢修操作过程复杂性的定义，本文选用第二种思路进行复杂性测度。

1　改进信息熵的操作过程复杂性测度模型

一个操作过程可以进一步划分为多个操作步骤，操作步骤可以进一步划分为粒度更大的操作步骤，直到不能划分为止。因此，根据粒度的不同，操作过程可以由不同的操作步骤通过一定的关系进行组合而成。每个操作步骤复杂性都有若干个影响因素。每个影响因素对复杂性的贡献越大，则该操作步骤的复杂性越大。由于信息熵是与概率紧密相连的，因此，这里用达到每个因素的概率作为对其评价，这样就可以用概率来衡量不确定性，进而用不确定性评价复杂性。根据普通的信息熵理论，当各个状态发生概率相等时，不确定性最大。按照此理论，当每个因素都等于0.2或都等于0.8时，复杂性是相同的，这显然与实际是不符的。因此，不能用普通的信息熵进行操作过程复杂性测度，需要对普通的信息熵进行改进。设某个步骤的复杂性影响因素共有n个，在该因素下能够顺利完成任务的概率为pi，则该因素造成的不确定性为其自信息熵：-lnpi。则所有因素造成的总不确定性为：

其中wij为第i个操作步骤的第j个影响因素的权重。可由专家通过AHP法获得。pij为第i个操作步骤的第j个影响因素下完成任务的概率。则共有m个步骤的操作过程的不确定性为：

因为在执行抢修操作过程中可能有多种执行路径，执行过程中需要操作者作出选择，由选择引起的不确定性也需要考虑。这些路径由选择节点确定。设抢修操作过程中共有m个选择节点，第i个选择节点处共有ni种路径可供选择，则根据信息熵理论由路径的多样性造成的不确定性为：

根据熵的可加性原理［6］，操作过程总的复杂性为：

2　操作步骤复杂性贡献因素的分析

2.1影响因素的组成［8］

操作步骤是操作过程的组成单元，根据粒度的不同，操作步骤也有区别。但是影响操作步骤复杂性的因素却是相同的。抢修操作是利用工具、设备或徒手对损伤的装备进行修复的工作。抢修操作对精度的要求越高，操作越复杂：无论是电子装备还是机械装备对精度的要求越高，操作时越小心，操作越细致，所消耗抢修员的精力及时间越长；抢修操作步骤对技巧、经验的要求越高，操作的难度越大，其复杂性越高：抢修过程不同于平时维修过程，因为抢修操作大多是非常规操作，因此，其对技巧与经验的依赖更强；操作步骤对技术水平的要求越高，抢修操作步骤的难度越大、复杂性越强：技术水平与技巧不同，技巧并不一定需要很高的技术水平，只需熟练即可，而技术水平则是对其知识、技能的综合考虑，显然所需的技术种类越多，所需技术等级越高，操作步骤的难度就越高，其实现的不确定性就大；操作步骤对体力的要求越高，操作的复杂性越高：抢修操作尤其是对大型复杂装备的抢修操作是一个非常消耗体力的行为（如在没有吊车的情况下拆卸身管）。由于在疲劳的情况下人犯错的几率明显增大，因此，抢修操作步骤对体力的消耗愈大，其行为的不确定性就越高，操作的难度就越强；由于抢修操作的复杂性，许多抢修步骤往往需要多人协同才能完成（如拆卸某高炮的炮尾），参与协同的人员越多，人员之间的差异就越明显，需要协调的工作就越多，不确定性明显增加；抢修操作的危险性越高，抢修步骤的复杂性越强：抢修操作与平时维修相比其危险性更高，显然其操作的危险性越大，在操作过程中需要消除该危险性，要做的额外工作越多，操作的不确定性越大，难度越高；操作空间越小，操作实施的难度越大。因此，影响抢修操作步骤复杂性的因素主要有以下7个，如图1所示。

图1　操作步骤复杂性影响因素构成

2.2单影响因素难度系数求取［9］

一般来讲影响因素的要求越高，操作的难度越大，完成任务的概率越小。直接求取单因素下抢修操作步骤的完成概率难度较大。但是操作难度与任务的完成概率互为相补关系。因此，通过求取难度系数，然后通过求其互补数来求取完成概率是可行的。一般来讲，难度系数函数D（x）应当满足以下两个条件：

①D（x）是x的分布函数F（x）及x的单调增函数；

②D（x）与F（x）在x点的增加速率相反，即：

∀x1∈R，x2∈R，△x＞0，可以实现以下推导

因此，可以得出满足上述两个条件的方程为：D（x）=aF-1（x）+b，其中F-1（x）为分布函数F（x）的反函数，a＞0，b∈R为调节参数。下面对上述两个条件进行证明：

①设有x1＞x2，D（x1）=aF-1（x1）+b，D（x2）=aF-1（x2）+b，因为F-1（x）与F（x）具有相同的单调性，这里以增函数为例，所以可得F-1（x1）＞F-1（x2），又因为a＞0，所以aF-1（x1）+b＞aF-1（x2）+b，进而得：D（x1）＞D （x2）；当F（x）为减函数的情况下，推导过程类似，所以条件1得证；

②令F（x）在x1处比在x2处增加的快，可得：

所以可得各个因素下任务完成概率的求取步骤如下：

①利用χ2拟合检验法，得出每个因素的分布函数F（x）；

②求取F（x）的反函数F-1（x）；

③令D（x）=aF-1（x）+b∈［0，1］，求取a，b的值；

④利用D（x）的补数求取其完成概率，即：

P（x）=1-D（x）。

由于各个因素中太大或太小的值出现的概率都较小，而中间部分出现的概率较大，且由于操作步骤的数量值趋于无穷大。因此，可以用标准正态分布φ（x）来代替每个因素的分布函数F（x）。即：

由于φ（x）是单调增函数，因此，其存在唯一的反函数φ-1（x），且，又因为D（x）∈［0，1］，所以可得各操作因素的难度系数方程为：

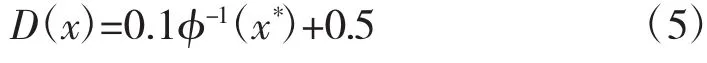
，μ为所有因素可能取值的均值，σ为所有因素可能取值的标准偏差，这里为抢修操作过程中所有操作步骤中该因素的均值与标准差。利用极大似然估计法可得上面两个参数的估计值：

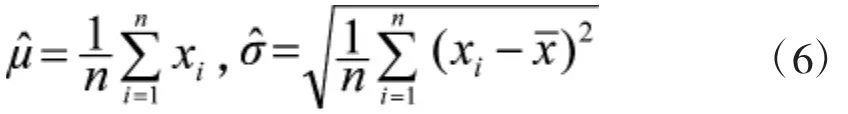
2.3影响因素的赋值

根据心理物理学研究结果可知，普通的线性关系赋值，不能反映各个等级之间真实的关系［10］。根据STEVEN定律，各等级之间的关系应当是非线性的关系，如指数关系和幂关系，其中Steven证明这种关系更倾向于幂关系［11］。因此，这里将五级评价等级按传统的线性赋值按照如下关系改造为幂赋值。

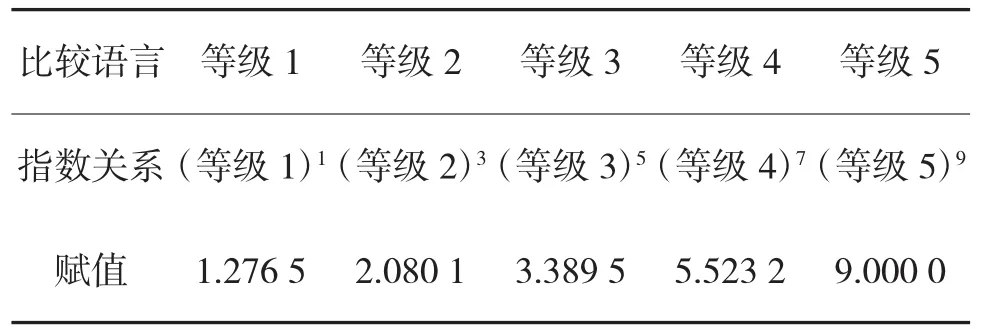
表1　因素等级的幂赋值

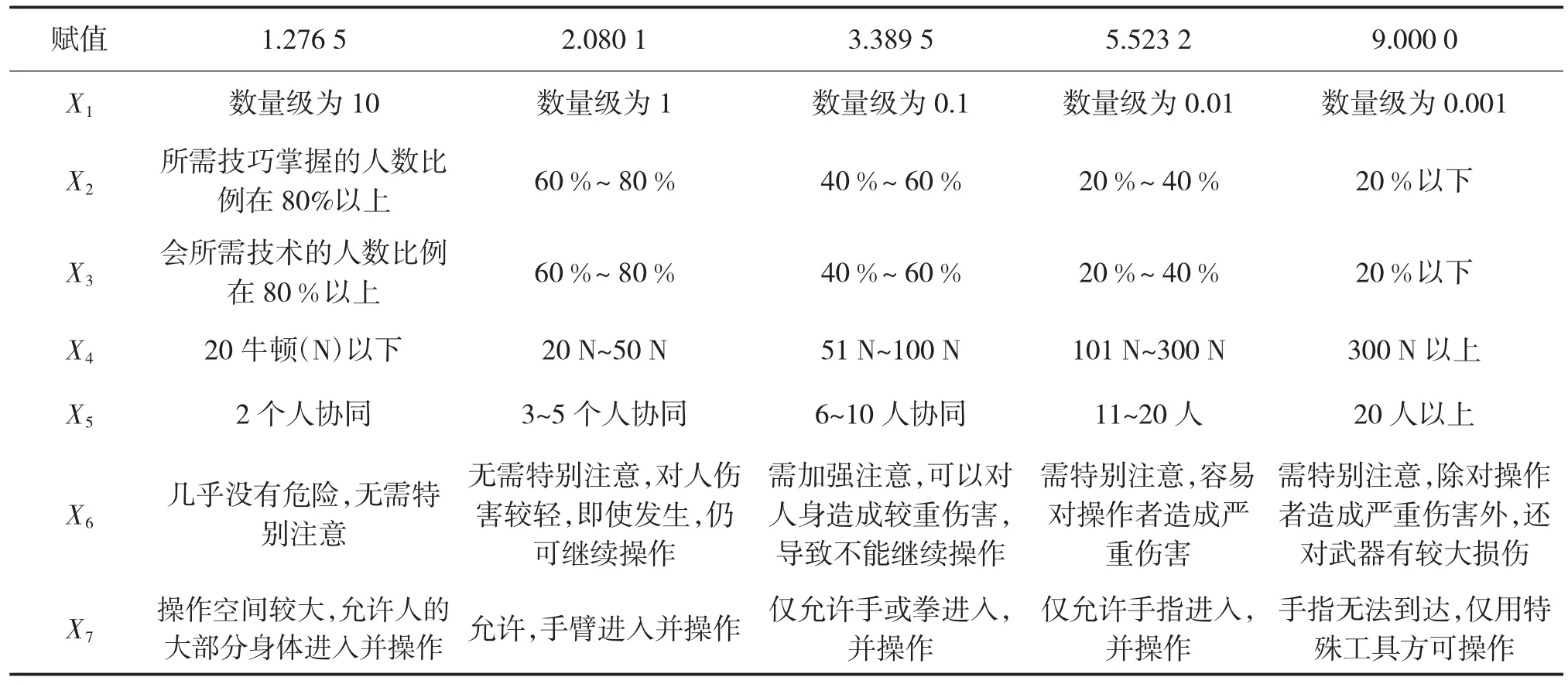
表2　影响因素赋值标准

2.4影响因素权重的确定

层次分析法是确定权重时应用最方便，也是应用最多的算法。然而普通的层次分析法大都采用1～9标度，这种标度方法的精确度不高，对于方案的优选与排序问题较为实用，而对于评估、预测问题则显得较为粗糙。部分学者将指数标度法引入层次分析法，取得了较好的效果［12］。指数标度法认为各等级之间具有如表3所示的指数关系：

表3　指数标度中等级关系

表4　指数标度中各等级赋值

则根据该标度方法获得判断矩阵A，由2.2可知指标数量为7，则得A=n×n，按照原始的方法求此矩阵的特征向量所对应的特征值作为权重；并对此判断矩阵进行一致性检验，通过对一致性比率的判断来判断所得权重结果是否合理，如表5所示。

表5　操作步骤复杂性影响因素的判断矩阵

所得权重w=（0.058 4，0.190 1，0.257 8，0.111 8，0.119 0，0.139 7，0.123 2），CR=-0.61＜0.1，所以结果合理。

3　模型有效性验证

3.1复杂性测度步骤

综合本文的以上论述，可以将抢修操作实施过程的复杂性测度步骤归纳如下：

①将抢修操作过程按照粒度分解为不同的抢修操作步骤，设共有n个操作步骤；

②按照评分标准（见表2）给每个抢修操作步骤的每个因素赋值，设xij为第i个步骤中第j个因素的赋值；

④求取各个操作步骤中每个因素的标准分：

⑤将每个抢修操作步骤中每个因素的标准分带入式（5）得到每个因素实施的难度贡献系数dij：dij=0.1φ-1（x*）+0.5；

⑥利用互补公式求取第i个步骤中第j个因素下抢修操作完成的概率pij为：pij=1-dij；

⑦联合式（1）～式（4）可得抢修操作过程复杂性。

3.2模型有效性验证

根据抢修操作过程复杂性的定义可以得出，抢修操作复杂性是抢修操作时间、抢修操作的出错率、抢修操作的任务完成概率、抢修操作实施难度等指标的抽象与综合。通过上述模型所获得的复杂性测度结果的有效与否可以利用这些指标进行验证。可以利用这些指标单独进行验证，也可以几个指标进行综合验证。由于抢修操作时间的已获取性及重要性，这里将抢修操作时间作为验证的对象，从已有的抢修数据库中，搜集具有时间参数的抢修操作，并按照上述模型计算抢修操作实施过程的复杂度。这样可以获得一组由抢修操作过程复杂度和抢修操作过程实施时间组成的样本数据集，通过对这组数据集进行回归分析，可以得出复杂度与时间之间的依赖关系，回归效果好则说明两者具有较强的相关性，模型的有效性高；回归效果不好则说明两者之间没有必然的关系，这与实际情况不符，模型的有效性差［13］。通过对所获的数据样本（表6）进行回归分析的结果（图2）分析可知：R2=0.812 7，R2-Ajust=0.750 2，回归效果较好，模型的有效性较强。

图2　回归分析结果

表6　数据样本

4　实例

为进一步验证模型的应用效果，这里以一个实例进行说明。受到敌人轰炸，某火控雷达和武器系统之间的电站专用输出插座被炸坏，电站功能完好，无法实现电源输出，雷达不能接电工作。这样，整个火力打击系统的“自动火力控制系统”也就陷入了瘫痪状态。经现场进行战损评估，认为虽然电站专用输出插座被炸，无法对原件进行修复，因此，采用抢修方法进行处理。在抢修方案中将抢修步骤进一步细分为抢修作业，将抢修作业作为粒度更大的抢修步骤看待。抢修操作过程逻辑如图3、下页表7所示。

图3　抢修实施过程逻辑流程

利用本文提出的模型，得出其步骤自身引起的复杂性IP（i）=9.008 2，抢修实施过程中只有一个选择节点，其概率分别为0.63与0.37，则逻辑复杂性IL=-log2（0.63）-log2（0.37）=2.101 0，则整个抢修操作过程的复杂性为：11.109 2。

利用回归分析结果y=0.806 1*x1.554-15.5，进行预测，其时间为18.49 min，而实际时间为16.90 min，相对误差为9.42%，满足要求。

5　结论

结合抢修操作过程特点引入抢修操作过程复杂性的定义，并利用改进的信息熵法建立了其复杂性测度模型，最后通过实例证明了模型的正确性。利用复杂性测度的结果可以辅助抢修人员准确估计抢修操作过程的难度与不确定性程度，为进一步实施抢修任务指派及抢修训练需求确定提供科学的、准确的依据。

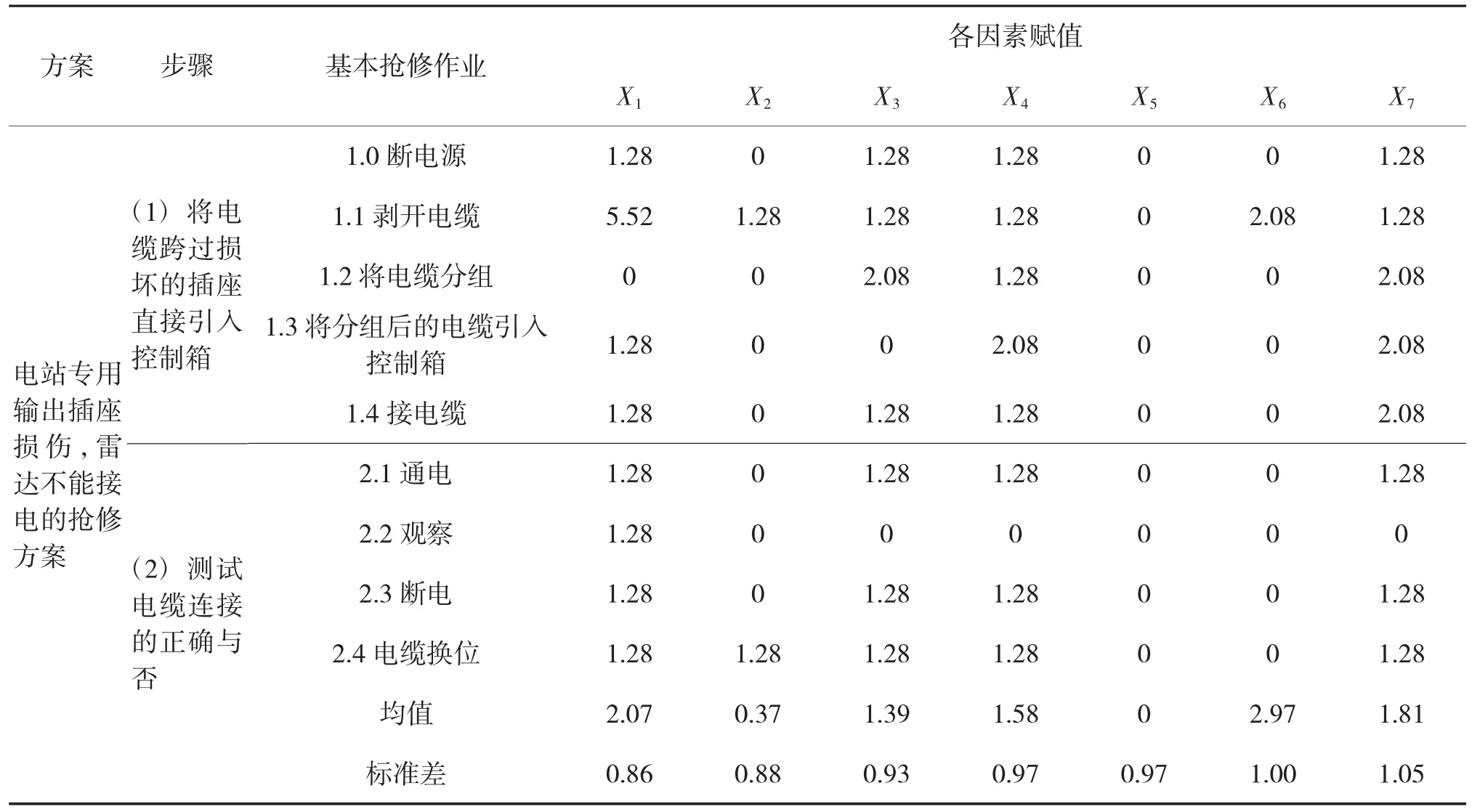
表7　电站专用输出插座损伤，雷达不能接电的抢修方案

参考文献：

［1］李建平，石全，甘茂治.装备战场抢修理论与应用［M］.北京：兵器工业出版社，2000.

［2］EFSTATHIOU J.The utility of complexity［J］.Manufacturing Engineer，2002，81（2）：73-76.

［3］饶运清，EFSTATHIOU J.基于信息熵的制造系统复杂性测度及其在调度中的应用［J］.机械工程学报，2006，42 （7）：8-13.

［4］王振宇.程序复杂性度量［M］.北京：国防工业出版社，1997.

［5］张延禄，杨乃定.项目复杂性内涵、特征、类型及测度方法的研究综述［J］.管理评论，2013，21（3）：15-17.

［6］邱菀华.管理决策熵学及其应用［M］.北京：中国电力出版社，2011：168-173.

［7］VIDAL L A，MARLE F，BOCQUET J C. Using a delphi process and the analytic hierarchy process（AHP）to evaluate the complexity of projects［J］. Expert Systems with Applications，2011，38（5）：5388-5405.

［8］石全，杜晓明，王润生.装备战伤评估理论与技术［M］.北京：国防工业出版社，2007：39-60.

［9］马建华.难度系数评分法［J］.工科数学，2001，17（1）：16-19.

［10］孙华，左曙光，杨占春，等.轿车乘坐舒适性主观感觉评价及实践［J］.同济大学学报，2001，29（2）：239-242.

［11］李永建，田清，傅浩，等.知识作业难度计量的脑电实验研究［J］.管理工程学报，2008，22（4）：51-55.

［12］舒康，梁镇韩.AHP中的指数标度法［J］.系统工程理论与实践，1990，11（1）：6-8.

［13］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2001.

Complexity Metrics Model for BDAR Operating Process Based on Extend Shannon Entropy

YOU Zhi-feng，LI Zhen，HU Qi-wei，TIAN Xia
（Ordnance Engineering College，Shijiazhuang 050003，China）

Abstract：BDAR operating process is the important index for BDAR person to confirm the difficulty and uncertainty of rush repair process. It is also the major conference for commander to assign the rush repair task and to schedule the rush repair resources. And it is the big part for assessing the rush repair time. Nevertheless，there is not appropriate method for BDAR operating process complexity metrics. Conferencing the fact that the maximum axiom of Shannon entropy is not consistent with the complexity characteristic of BDAR operating process，the extend Shannon entropy is introducing to measurement the complexity degree of operating process. At last，an example to check up the complexity metric method using regression analysis is given. By the result，this model can objectively measurement the complexity of BDAR operating process.

Key words：BDAR operating process，complexity metrics，extend Shannon entropy，difficulty coefficient，regression analysis

中图分类号：TJ07

文献标识码：A

文章编号：1002-0640（2016）05-0080-06

收稿日期：2015-04-21修回日期：2015-05-18

作者简介：尤志锋（1980-），男，河北行唐人，博士，讲师。研究方向：战场抢修，复杂性及测度，计算机建模与仿真方向。