云模型改进惯性权重的混沌交替粒子群算法*

李纪真，孟相如，崔文岩，杨　婷

（1.空军工程大学信息与导航学院，西安　710077；2.解放军95133部队，武汉　430415）



云模型改进惯性权重的混沌交替粒子群算法*

李纪真1，孟相如1，崔文岩1，杨婷2

（1.空军工程大学信息与导航学院，西安710077；2.解放军95133部队，武汉430415）

摘要：标准粒子群算法通过线性减小惯性权重系数来调整寻优性能，但缺乏智能化机制易导致算法后期产生早熟或陷入局部最优而产生僵局。针对这一问题，提出一种基于云模型改进惯性权重的混沌交替粒子群优化算法。根据粒子迭代变化关系，采用云模型理论对惯性权重ω进行智能化调整，以平衡其全局和局部搜索能力，防止算法产生局部僵局；另外，判定粒子稳定性，对于可能陷入局部僵局的稳定粒子进行混沌扰动，促使其跳出僵局进而向最优位置更新。实验与分析表明，基于云模型改进惯性权重的混沌交替粒子群优化算法能够跳出局部僵局且具有较高的寻优精度，算法接近完全收敛时的平均迭代次数，较现有相关研究分别降低了13.73%～20.11%。

关键词：粒子群，云模型，惯性权重，稳定粒子，混沌交替

0　引言

粒子群优化算法（Particle Swarm Optimization，PSO）是1995年由Kennedy博士和Eberhart博士受鸟类捕食行为启发而发明的一种进化计算技术［1］，它是一种智能优化算法，具有参数少、易实现、收敛快等特点，广泛应用于各领域中的最优化求解问题。但是，标准粒子群算法存在易陷入早熟和局部最优等问题，使其在求解最优化问题时不能充分发挥效能［2］。

为此，相关研究对标准粒子群算法进行了改进，主要体现在以下两个方面：一是通过参数优化对更新公式进行调整进化，如文献［3］提出一种基于粒子圆周轨道和零惯性权重的粒子群算法，但该算法设置较为复杂且只能解决离散问题，使得算法的应用受到限制；文献［4］通过使用时变的非线性三角函数方法来控制粒子群算法参数，但并未给出用三角函数控制粒子参数的理论依据；文献［5］将粒子线性移动改进为非线性移动方式，并提出一种新的粒子修复策略，但该修复策略无法保证粒子具有合理的移动速度；文献［6］提出一种与禁忌搜索法相结合的混合粒子群算法，对算法主要参数作了改进并引入约束处理机制，但算法过于依赖所制定的约束条件。二是基于混沌思想对标准粒子群算法进行改进，衍生出混沌粒子群优化算法（Chaos Particle Swarm Optimization，CPSO），可以在一定程度上解决标准粒子群算法存在的问题，如文献［7］提出一种基于Logistic映射的基本混沌粒子群算法，但该算法在未设置混沌扰动条件的情况下对所有粒子进行混沌扰动，显得有些盲目；文献［8］提出一种基于序贯二次规划（SQP）的混沌粒子群算法，在满足一定条件下依概率进行混沌扰动，但未考虑概率条件对混沌扰动的影响；文献［9］将混沌融入到粒子运动过程中，使粒子群在混沌与稳定之间交替进化，但该算法将粒子每一维进行混沌扰动后都计算粒子适应值，加大了算法的复杂度；文献［10］采用云模型对最优个体进行小生境局部搜索，并根据Cat映射完成全局混沌搜索，但仅通过全局搜索识别参数判定进行局部或全局搜索，没有严格的数据支撑，缺乏科学性。

针对上述问题，本文从参数优化和混沌扰动思想两方面对粒子群算法进行改进，提出一种基于云模型改进惯性权重的混沌交替粒子群优化算法，以求能够更好地求解最优化问题。改进算法根据当前粒子的适应值与当前所有粒子的平均适应值之间的关系，采用云模型来模糊处理粒子群算法的惯性权重ω，从而达到智能动态调整ω的要求，平衡算法的全局搜索能力和局部搜索能力。另外，对于可能陷入局部最优的稳定粒子进行Logistic混沌扰动，促使粒子跳出局部最优，混沌与稳定交替迭代运行，进一步防止算法陷入早熟。为了验证本文改进算法性能，将其与几种现有混沌粒子群算法通过测试函数的优化求解问题进行对比分析，实验结果验证了本文改进算法能够以相对较快的收敛速度跳出局部最优。

1　理论基础

1.1标准粒子群算法

设搜索空间为D，群体规模为n。第i个粒子的位置矢量为zi=（zi1，zi2，…，ziD），根据适应值函数计算zi可以衡量粒子位置的优劣；第i个粒子的位置变化率为Vi=（vi1，vi2，…，viD）；Pi=（pi1，pi2，…，piD）为粒子迄今为止搜索到的最优位置；Pg=（pg1，pg2，…，pgD）为整个粒子群迄今为止搜索到的最优位置［11］。粒子根据下式更新速度和位置：

其中，i=1，2，…，n，d=1，2，…，D，t为迭代次数，ω为惯性权重，可调节算法的全局和局部寻优能力；c1和c2为正常数的学习因子，使粒子具有自我总结和向群体中优秀个体学习的能力，从而向自身的历史最优位置以及群体的历史最优位置靠近；r1和r2为［0，1］之间的随机数，用来保持群体的多样性［12］。

1.2云模型理论

云模型（Cloud Model）是李德毅院士基于模糊逻辑和概率论提出的一种处理定性概念与定量数值表示之间不确定性的转换模型，为不确定性人工智能提供了新的研究方法，云模型理论在智能控制、数据挖掘、模糊评测等方面得到了广泛应用和较好效果［13］。

设集合U=｛x｝为用数值表示的定量论域，Cn是U上的定性概念，若定量值x∈U是定性概念Cn的一次随机实现，x对Cn的确定度μ∈［0，1］是有稳定倾向的随机数，则x在论域U上的分布称为云，记为云C（x），每一个x称为一个云滴［14］。

云模型可用3个数字特征（Ex，En，He）来描述，期望值Ex对应于隶属度最大的基础变量，即最能代表定性概念的点，它标定了云对象在论域中的重心位置；熵En是定性概念模糊程度的度量，其大小直接决定了在论域中可被模糊概念所接受的范围；超熵He是隶属度函数随机性的度量，其大小间接地反映了云的厚度。正态云模型是最具普适性的一种云模型，具有良好的数学性质，如图1所示，其数学期望曲线（Mathematical Expected Curve，MEC）可表示为MEC（x）=exp［-（x-Ex）2/2En2］。

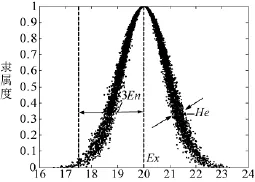
图1　一维正态云模型分布示例

图2所示为正向云发生器（Forward Cloud Generators，FCG），它根据已知正态云模型的数字特征（Ex，En，He），在给定论域数值x或确定度μ的条件下，产生满足上述云模型分布规律的云滴drop（x，μ）［15］，实现将一个定性概念通过云模型的不确定性转换而定量地表示出来。正向云发生器的实现算法如表1所示。

图2　正向云发生器

表1　正向云发生器实现算法描述

2　云模型改进惯性权重的混沌交替粒子群优化算法

2.1云模型调整惯性权重

PSO算法惯性权重ω的选取很大程度上决定了算法的执行效果，其取值范围一般在［0，1］。标准PSO算法通过线性减少ω来调整算法性能，但容易在全局最优解附近发生“交叉震荡”现象，从而使算法陷入局部极值，影响收敛速度，增大算法全局寻优的难度。ω是对PSO算法全局搜索与局部搜索性能的平衡参数：当粒子与全局最优解相距较远时，需增大ω值来提高粒子飞行速度，增强算法的全局搜索能力；较小的ω会增强算法的局部搜索能力，当距离全局最优解较近时，则需减小ω值来降低飞行速度，进行局部细化搜索。

与文献［11］采用云模型对收敛区域局部求精不同的是，本文将根据粒子位置的实时更新情况，尝试采用云模型对PSO算法的惯性权重ω进行智能动态调整，达到平衡算法全局与局部寻优能力的目的，防止产生局部最优问题。具体的：令，其中f为当前粒子的适应值，favg为当前所有粒子的平均适应值，则，即这里将确定度μ记为FCG则对惯性权重ω的改进机制如式（2）所示：

其中，ωmax为惯性权重的最大值，FCG为经过云模型模糊处理的惯性权重系数。由式（2）可以看出：当favg≤f时，即当前目标函数值优于平均目标函数值时，通过ω=ωmax*FCG使惯性权重变小，从而保护该粒子；当favg＞f时，即当前目标函数值差于平均目标函数值，通过ω=ωmax使惯性权重变大，从而使该粒子向较优的搜索区域靠拢。该机制通过智能调整ω，平衡了PSO算法的全局搜索能力和局部搜索能力，有效防止PSO算法陷入局部僵局而发生“交叉震荡”现象。

2.2混沌交替粒子群优化思想

文献［9］提出混沌与稳定交替迭代更新的粒子群算法，但将粒子每一维进行混沌扰动后都计算粒子适应值，加大了O（D）的时间复杂度，影响算法执行效率。本文改进算法在对稳定粒子引入混沌扰动时，将粒子所有维进行混沌扰动后再带入适应值函数Fiteness，进而计算个体最优和全局最优，与文献［9］中的方法相比降低了O（D）的时间复杂度，提高了算法效率。通过式（3）判断粒子是否处于稳定状态［9］，其中，move代表粒子当前移动距离，stable代表粒子当前位置与历史最优位置的距离。

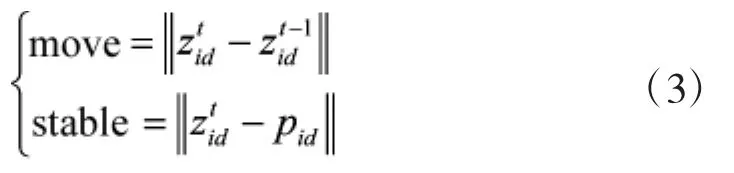
在每次迭代中先判断粒子稳定性，当move＜10-6&&stable＜10-6&&t＜0.9T时（T为总迭代次数），表示粒子稳定，需要引入混沌，对稳定粒子变量进行Logistic混沌扰动［8］，即，促使可能陷入局部最优的粒子跳出局部最优；当stable＞10-6&&t＜0.9T时，表示粒子不稳定，无需进行混沌扰动，粒子正常通过迭代向最优值靠近。混沌与稳定的交替使粒子不断向最优解靠近［9］。

2.3算法描述

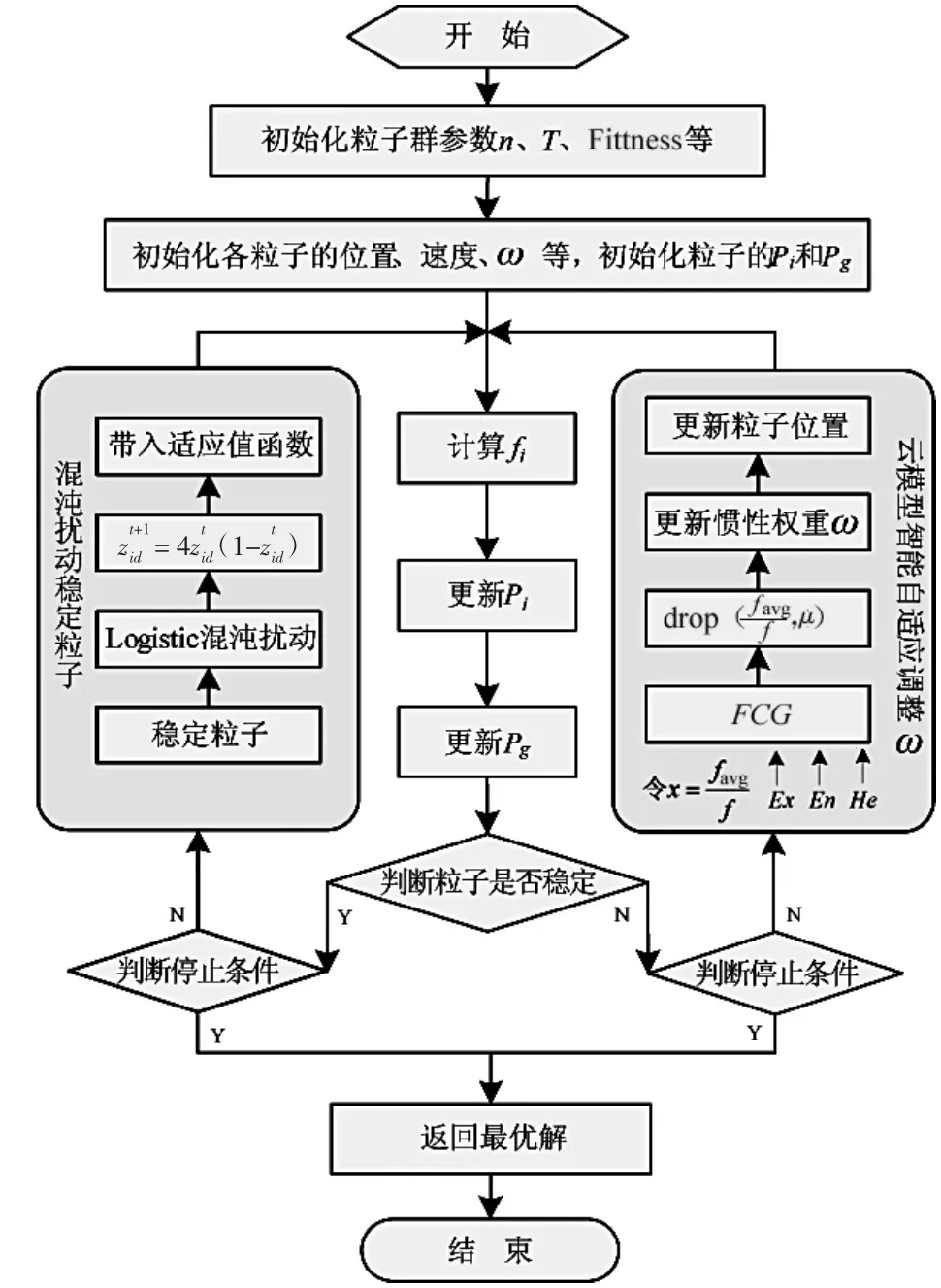
图3　云模型改进惯性权重的混沌交替粒子群算法流程

基于云模型改进惯性权重的混沌交替粒子群优化算法流程如图3所示，算法详细描述如下：

Step1初始化：包括种群规模n，最大迭代次数T，适应度函数Fitness等，随机产生粒子的位置、速度和惯性因子ω等，初始化粒子的Pi和Pg；

Step2计算适应度：根据适应度函数Fitness计算出每个粒子的适应度值fi；

Step3更新Pi和Pg：对于每个粒子，根据fi值，将粒子当前位置与它经历过的最好的位置Pi进行比较，如果当前位置更好，则将其更新为当前的最好位置Pi，否则Pi保持不变；对于每个粒子，根据fi值，将粒子当前位置与群体中所有粒子所经历过的最好的位置Pg进行比较，如果这个粒子的位置更好，则将其更新为当前的最好位置Pg，否则Pg保持不变；

Step4判断粒子是否稳定：若当前粒子满足稳定条件，则执行Step5；若不满足，则执行Step6；

Step5混沌映射：若满足停止条件，执行Step8。若不满足停止条件，对当前稳定粒子进行Logistic混沌映射，返回Step2继续执行；

Step6判断是否满足停止条件：若满足停止条件，执行Step8。若不满足停止条件，执行Step7；

3　实验与分析

3.1测试函数及算法参数设置

将文献［8-10］中的混沌粒子群算法，以及本文提出的基于云模型改进惯性权重的混沌交替粒子群算法进行实验比较。试验方法是选用如表2所示的4个全局最优解为0的最优化函数进行寻优测试。

表2　测试函数

其中，Sphere函数全局最优点在X=（0，0，0，…，0），自变量-50≤xi≤50；Griewank函数全局最优点在X=（0，0，0，…，0），自变量-600≤xi≤600；Rosenbrock函数全局最优点在X=（1，1，1，…，1），自变量-100≤xi≤100；Rastrgin函数全局最优点在X= （0，0，0，…，0），自变量-5.12≤xi≤5.12［9］。

PSO算法的适应度函数即为上述4种测试函数，PSO算法惯性权重ω的调整机制如式（2）所示，其他参数设置如表3所示。云模型参数设置主要是对Ex、En和He进行设置，根据正态云模型的性质及经验，取Ex=0，En=1/3（云宽度μ=1），He=0.1，如表3所示。

表3　算法主要参数设置

3.2实验结果及分析

采用表2中的4种测试函数，在基本参数设置一致的条件下，将本文提出的基于云模型改进惯性权重的混沌交替粒子群优化算法与文献［8-10］中的算法进行寻优比较。经多次测试取平均值，得实验数值测试结果如表4所示。最优测试值与实际最优值的绝对误差如图4所示。

表4　数值测试结果

图4　最优测试值与实际最优值的绝对误差

由表4、图4可以看出，本文算法的寻优精度明显高于文献［8-10］中的算法。另外，各算法对4类测试函数寻优过程的对比结果，即迭代次数t与最优适应值对数函数lg（f（Pg））的关系，如图5所示。

基于云模型改进惯性权重的混沌交替粒子群算法，通过正向云发生器对算法惯性权重ω进行智能动态调整，并判定粒子稳定性，对稳定粒子进行Logistic混沌扰动，促进可能陷入局部最优的粒子跳出局部最优，并进一步向最优位置靠近。由图5也可以看出，本文提出的改进算法比文献［8-10］中的算法明显有效，且能够达到较高的寻优精度。

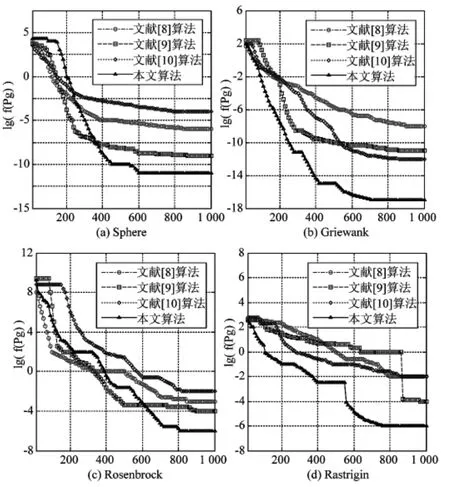
图5　各算法对4类测试函数寻优过程对比

另外，本文算法不仅能够跳出局部最优，还具有相对较快的收敛速度，图6所示为算法接近完全收敛时的迭代次数对比。可以看出，本文算法在接近完全收敛时的迭代次数较其他算法更少，平均迭代次数分别比文献［8-10］中的算法降低了16.37%，20.11%，13.73%。

图6　算法接近完全收敛时迭代次数对比

4　结论

针对标准粒子群优化算法及现有改进研究中存在的一些问题，提出一种基于云模型改进惯性权重的混沌交替粒子群优化算法，采用云模型理论对粒子群算法的惯性权重进行智能调整，以平衡算法的局部和全局搜索能力，防止其陷入局部最优；另外，对可能陷入局部最优的稳定粒子进行Logistic混沌扰动，以促使其跳出局部最优进而向最优位置靠近。通过实验验证分析，本文算法在寻优精度、迭代次数等方面具有良好的性能，有效解决了粒子群算法容易在后期陷入早熟和局部最优的问题。

参考文献：

［1］KENNEDY J，EBERHART R C. Particle swarm optimization ［C］// Proc of the First IEEE International Conference on Neural Networks. Perth，Australia：IEEE Press，1995：1942-1948.

［2］NERI F，MININNO E，LACCA G. Compact particle swarm optimization［J］. Information Sciences，2013，239：96-121.

［3］温涛，盛国军，郭权.基于改进粒子群算法的Web服务组合［J］.计算机学报，2013，36（5）：1031-1046.

［4］李光宇，郭晨，李延新.基于改进粒子群算法的USV航向分数阶控制［J］.系统工程与电子技术，2014，36（6）：1146-1151.

［5］齐建军，郭波，张涛.基于改进粒子群算法的地空导弹使用保障设备优化配置［J］.国防科技大学学报，2014，36 （1）：178-183.

［6］夏美梦，关富玲.基于改进粒子群算法的天线索网预应力优化［J］.浙江大学学报，2013，47（3）：480-487.

［7］YOU M，JIANG T. New method for target identification in a foliage environment using selected bispectra and chaos particle swarm optimisation-based support vector machine［J］. IET Signal Processing，2014，8（1）：76-84.

［8］徐文星，耿志强，朱群雄.基于SQP局部搜索的混沌粒子群优化算法［J］.控制与决策，2012，27（4）：558-561.

［9］胥小波，郑康峰，李丹.新的混沌粒子群优化算法［J］.通信学报，2012，33（1）：24-30.

［10］LI M W，KANG H G，ZHOU P F. Hybrid optimization algorithm based on chaos，cloud and particle swarm optimization algorithm［J］. Journal of Systems Engineering and Electronics，2013，24（2）：324-334.

［11］张朝龙，余春日，江善和.基于混沌云模型的粒子群优化算法［J］.计算机应用，2012，32（7）：1951-1954.

［12］简平，邹鹏，熊伟.混合离散粒子群的任务调度算法及应用［J］.火力与指挥控制，2014，39（5）：146-149.

［13］LIU S，CHANG X C. Synchro-control of twin-rudder with cloud model［J］. International Journal of Automation and Computing，2012，9（1）：98-104.

［14］王尚广，孙其博，张光卫.基于云模型的不确定性QoS感知的Skyline服务选择［J］.软件学报，2012，23（6）：1397-1412.

［15］LI M W，HONG W C，KANG H G . Urban traffic flow forecasting using gauss - SVR with cat mapping，cloud model and PSO hybrid algorithm［J］. Neurocomputing，2013，99：230-240.

Chaos Alternation Particle Swarm Optimization Algorithm Improved Inertia Weight Based on Cloud Model

LI Ji-zhen1，MENG Xiang-ru1，CUI Wen-yan1，YANG Ting2
（1.School of Information and Navigation，Air Force Engineering University，Xi’an 710077，China；2. Unit 95133 of PLA，Wuhan 430415，China）

Abstract：The optimization performance of the standard particle swarm optimization algorithm is adjusted by reducing the inertia weightlinear，which lack of intelligent mechanism and easy to bring into the prematurity and local stalemate in the evening of the algorithm. A chaos alternation particle swarm optimization algorithm improved the inertia weight based on cloud model is proposed to solve these problems. The inertia weight ω of the particle swarm optimization algorithm is adjusted by cloud model intelligently according to the iterative transformation of the particles，and the whole and local searching capabilities of the particle swarm optimization algorithm get balanced，and prevent it into the local stalemate. In addition，determine the stability of the particles，and do chaos disturbance to the stable particles which maybe bring into the local stalemate，make it jump out form the local stalemate and close to the optimization position further. It shows from the experiment and analysis that the chaos alternation particle swarm optimization algorithm improved the inertia weight based on cloud model can be able to jump out from the local stalemate with a higher optimization precision，and the average iterative numbers are reduced by 13.73%～20.11%than other researches when the algorithm gets absolutely convergence.

Key words：particle swarmoptimization，cloud model，inertia weight，stable particles，chaos alternation

中图分类号：TP18

文献标识码：A

文章编号：1002-0640（2016）05-0056-06

收稿日期：2015-04-17修回日期：2015-05-20

*基金项目：国家自然科学基金资助项目（61201209，61401499）

作者简介：李纪真（1986-），男，山东泰安人，博士生。研究方向：网络安全预警与响应决策。