浅析学习支架的应用

●白元伟　汪国荃



浅析学习支架的应用

●白元伟汪国荃

一、构建情境式教学

数学是开发人的逻辑思维能力的学科，但在初中数学课堂上，很多学生认为数学枯燥乏味，体味不到逻辑思维的乐趣。为了让学生主动参与到数学课堂学习中，教师应通过创设适当的情境，激发学生的好奇心和求知欲，促使学生愿意自己去思考问题、解决问题，从而达到对知识的建构，感受做逻辑体操的快乐。

如，笔者在教学《圆》一课时，引导学生联系生活中车轮等圆形物体形状设想，讨论车轮为什么要造成圆形。请学生想象骑着三角形、四边形车轮骑车的情形，学生就会兴奋起来，纷纷说：“不能！这样的轮子无法滚动。”笔者接着再问：“那就造成鸭蛋的形状吧！行吗？”学生开始感觉茫然，继而大笑起来：“若是这样，车子会忽高忽低的。”教师继续追问：“为什么造成圆形不会忽高忽低呢？”学生又一次活跃起来，纷纷议论，最终找到了答案——“因为圆形车轮上的点到轴心的距离处处相等”。这样自然而然地得到了圆的定义，收到了很好的教学效果。这样的教学方式，能够让学生在很自然的学习情境中掌握数学知识，能够取得较好的教学效果。所以，教学时创建情境非常重要，这是“支架式”教学中的一个非常重要的环节。

二、培养探究意识

在教学活动中，教师要重视对问题的设计，通过引导学生，把抽象的数学知识与实际内容联系起来，使学生的再认识转化为一个学习过程，培养探究问题的意识。通过学习支架的帮助，学生可以切身体验到数学思想产生的过程，从而对数学问题的理解变得更加准确、深刻。

如，学生在完成了“在△ABC中，∠B=25°，AD是BC边上的高，并且AD2= BD·DC，求∠BCA的度数”的求解后，笔者继续设计如下问题，激发学生的探究意识。出示图1，要求学生判断正误，并说明理由。

图1

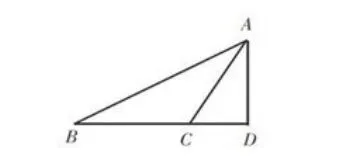
图2

∵AD是BC边上的高

∴∠ADB=∠ADC=90°

又∵AD2=BD·DC

∴BD∶AD=AD∶DC。

所以，△ABD∽△CAD，

故∠BCA=90°-25°=65°。

凭借已有经验，学生很容易发现解题的不足：图1中D点在BC边上，只有当△ABC是锐角三角形的时候成立。要得到正确解答，还应考虑什么问题？是D点的位置，还是△ABC的分类问题？笔者设计出一系列疑问，学生在好奇心的驱动下，热烈讨论、归纳，他们发现点D的位置可以在边BC上，也可以在BC的延长线上（当△ABC为钝角三角形时），如图2，此时，可解得∠BCA=115°。通过不断引导学生思考，创建学习支架，学生思考开始有条理性，他们学会了如何将问题进行分类，如何一步步分析探究，自主学习能力不断增强。

三、形成网络体系

数学知识具有一定的结构性，它不是封闭的“知识体系”，而是相互联系、动态活动的一个系统。教学过程中，教师要注意引导学生把所学的知识和实际应用结合起来，寻找知识间的相互联系，逐步形成纵向和横向的知识网络体系，扩充知识结构，逐渐培养学生构建学习支架及应用学习支架的意识和能力，提高知识的应用水平和效率。

如，已知关于x为变量的一元二次方程x2+2（m-1）x+3m2-11=0有实数根，问：是否存在实数m，使方程的两根x1、 x2满足若存在，求出方程的两根倒数和；若不存在，请说明理由。学生解答时出现了“”的值是“”或“”的错误，其原因是学生对一元二次方程概念的理解不到位，在解题时，没有考虑一元二次方程有实数根的条件，即根的判别式Δ≥0这个条件。在教学中，笔者结合学生解题中的错误，引导他们梳理链接以前学习的一元二次方程的概念，让学生认识到，涉及一元二次方程概念的问题时要注意的知识点。他们不仅要了解概念，还要了解根与系数的关系。

学习支架促使学生经历了一些更更为深刻的思维过程，有助于学生对知识结构，特别是隐性知识体系的感悟与理解。

（作者单位：丹江口市石鼓镇初级中学）

责任编辑严芳