基于Monte-Carlo仿真的机床大修项目工期及费用风险分析

周尔民，王贵用，王 健

（华东交通大学　机电工程学院，南昌 330013）



基于Monte-Carlo仿真的机床大修项目工期及费用风险分析

周尔民，王贵用，王 健

（华东交通大学机电工程学院，南昌 330013）

摘 要：在某机床大修项目中，运用双代号网络图进行分析，通过分析确定该项目的各个时间参数，然后在Excel上构建该网络计划项目的模型，再通过安装并运行Crystal Ball进行多次模拟，得到多次运行结果，并对这些结果进行统计。通过统计图或统计表，同时分析该项目的工期风险和费用风险，并从分析中获得有效的结果。在实际案例基础上，介绍了使用Crystal Ball和Excel对工程项目进行建模和风险分析的步骤和方法。

关键词：Crystal Ball；网络计划；双代号网络图；工期风险；费用风险

0　引言

项目管理是指运用各种专业知识、工具、技术和方法对项目进行有效管理，使其达到在尽量短的时间内，用尽量少的成本，较好地完成项目的预期目标［1］。

作为项目管理中常用的两种方法，关键路线法（CPM）和计划评审技术（PERT）在各行各业的项目管理中得到广泛的应用。关键路线法以经验数据确定项目活动时间，将其设定为确定数值，然后去寻找关键路线。而计划评审技术是通过悲观时间、最可能时间和乐观时间三个时间点来计算出工期，该方法主要注重对项目的计划进行评审。

关键路线法，是一个由节点和活动组成的网络图，用来说明项目中各个活动的时间参数，以及各个活动之间的关系，然后通过网络图计算各个活动的最早开始时间（TES）、最早结束时间（TEF）、最晚开始时间（TLS）、最晚结束时间（TLF），然后寻找网络中的关键活动，得到该网络的关键路线。通过对关键路线的改善，可以达到改善整个项目的效果。

CPM网络图采用关键路线法时网络图中紧前活动、后续活动、平行活动、虚拟活动的定义和绘制规则，以及节点最早开始时刻、节点最迟完成时刻、活动宽裕时间等的计算方法完全与计划协调技术相同。

在项目管理中M Bevilacqua和H Steyn等人提出在项目管理中运用关键链方法［2，3］。美国海军提出了PERT应用于计划和控制导弹的研制。这两种方法均不能考虑到项目管理中存在很多不确定性因素，为了解决这个问题，本文运用现在较为前沿的项目管理风险分析方法，基于Crystal Ball的蒙特卡洛仿真。

尹齐心，余明晖和刘振元考虑了工程项目中的间接成本，建立了工期一成本一质量之间的非线性综合优化模型，并运用遗传算法进行求解，但是没有考虑到以多大概率能在预定的时间和成本内完成工程项目［4］。张静文和单绘芳将资源分为可更新和不可更新两类，并考虑了两类资源约束条件下的工期一费用均衡调度模型，然后运用两阶段混合优化算法对该调度模型和传统的经典离散时间一费用调度模型进行对比，分析了两类资源约束条件下所建立模型的优越性［5］。张立辉，乞建勋，仲刚在CPM网络基础上，提出了一种总工期敏感性的分析方法，并提出了在CPM中主路线等概念以及总时差定理，分析了关键路线的重要性，以及关键工序工期对总工期的影响，分析了总工期的敏感性问题［6］。曹小琳和刘仁海综合介绍了多种缓冲区计算方法，并在此基础上，提出了缓冲区大小的影响因素，以及缓冲区的大小对项目计划工期和项目进度内完工概率的影响，但是该文只提到缓冲区的重要性，并未提到如何通过缓冲区的大小来计算计划进度内的完工概率［7］。赵道致，王元明提出工期风险受项目本身及环境因素的影响，研究了在PERT的项目中，单时段以及全时段的工期风险，并分析了工期风险的传递规律［8］。蒋玉石和史本山利用Monte-Carlo模拟一种计算口碑价值的模型，并利用Crystal Ball软件进行模拟计算，可见Crystal Ball软件对于Monte-Carlo模型求解的有效性［9］。

李江和雷晓刚提出一种结合Multi-Agent和分布式仿真相结合的项目管理方法，并将其应用于大型航天研发项目风险分析，但该方法只分析得到该项目以多大概念处于哪一个范围的风险，而没有具体计算出风险的大小，而且该方法不适用于具体的工期及费用风险分析［10］。郭宇和刘尔烈在以往用于项目成本风险分析的蒙特卡罗方法的基础上，提出了一种考虑成本要素依赖关系的成本风险计算方法，该方法适用于对成本影响的因素较为复杂的场合，而且不能进行工期风险分析［11］。高建伟指出了对项目进行风险量化管理的必要性，并且定义了基于蒙特卡洛仿真的抽样算法与流程，并提出了计算项目完工概率的方法，但是并没有进行项目的成本风险分析［12］。Crystal Ball正是基于蒙特卡洛的仿真工具，它可同时进行成本和工期风险的分析。孟宪宽和邹磊提出了将关键链理论和网络计划技术相融合对项目管理进度进行分析的思想，利用Crystal Ball在Excel中建立模型就是基于这种思想［13］。孙金梅和刘海涛通过Excel建立模型，并求解出模型的关键路线，并对工期和费用进行优化，但是并没有考虑到活动时间的不确定性，并且没办法计算工期和费用存在的风险［14］。杨琴和胡辉用Crystal Ball在Excel中建立项目管理的模型，并对模型进行工期风险的分析，结合具体例子分析项目的完工概率，但是没有对项目的费用风险进行分析［15］。

从以上这些研究成果我们可以看出：第一，对于项目风险的分析，大部分只对工期进行分析，对工期—费用同时进行风险分析，还有待进一步研究；第二，运用关键路线对风险进行分析时，没有考虑到各个工序工期和费用的不确定性，而运用计划评审技术对风险进行分析时，没有考虑到各个工序先后顺序的制约性；第三，在研究风险时，已有的研究偏向于对项目的一些变量做出假设，以简化分析过程，对分析结果的真实性有一定偏差；第四，大部分的风险分析都是运用于工程建筑方面，而对于机械工程方面的项目风险分析还有待进行［3～15］。

针对这些不足，本文同时对项目的工期—费用进行分析；综合考虑关键路线和计划评审的优势；同时考虑各个工序先后顺序的制约性和各个工序工期和费用的不确定性，创建Crystal Ball项目工期和费用的风险分析模型，使得工序的工期可以在最小完工时间和最大完工时间之间波动，同时工序之间又按照网络图的先后顺序相互制约；本文所用的Crystal Ball是基于蒙特卡洛仿真的风险评估软件，较接近项目的真实完成情况。

本文的研究对于机械工程方面的项目风险分析研究，做了进一步的尝试，对于后续的研究，做了一点基础工作。同时本文对项目的工期—费用同时进行分析，并对风险进行量化，给出了具体存在风险的大小。

1　机床大修的项目计划

某工厂有一个机床大修的项目计划，该大修项目包括十道工序，各道工序所需的工时服从三角型分布。各道工序的先后顺序、工时分布的参数、工序名称以及各道工序单位工时所需支付的工资如表1所示。对于该项目的工期要求不能超过27天（按每天8个工作小时计算，即216小时），该项目的直接费用不能超过2150元，要求建立模型，进行分析、预测该项目延期的风险和超出预定费用的风险。

2　建立一个Excel模型

2.1绘制该项目的网络图

根据表1所给的各个工序的前后关系，并合理的增加虚工序绘制该网络计划的双代号网络图，如图1所示。

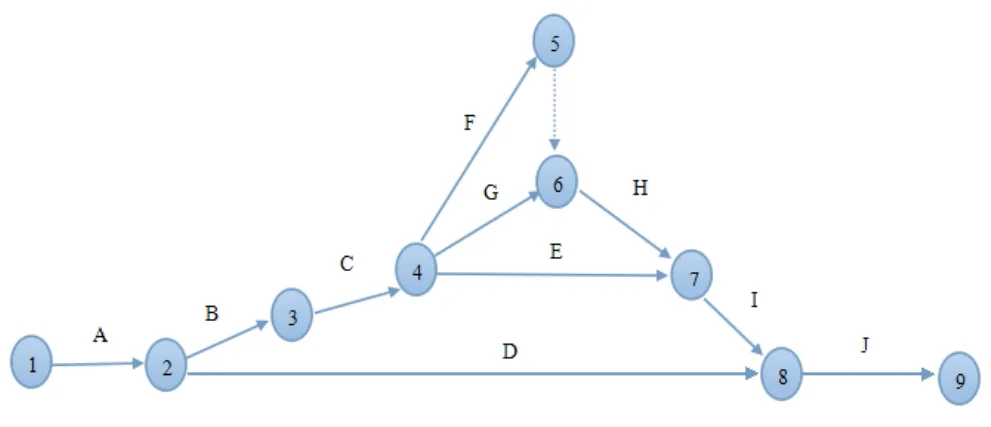
图1　该项目的双代号网络图

2.2网络中各活动的时间参数计算方法

定义活动A的最早开始时间TES（A）=0，然后依次计算其他活动的最早开始时间，TES（X）=TEF（前）；各工序的最早结束时间TEF（X）=TES（X）+D（X），工期T=TEF（J）；J工序的最迟结束时间TLF（J）=T，其他活动的最迟结束时间TLF（X）=MIN（TEF（前））；各工序的最迟开始时间TLE （X）=TLF（X）-D（X）；从而得到各工序的总时差S （X）=TLS（X）-TES（X），其中总时差为0的活动就是关键活动，否则为非关键活动。

各个工序所需费用等于取整后的持续时间乘以各个工序单位工时所需的工资。如A工序所需的工资在图2中为M（A）=16×7=112。

总费用等于各个工序所需的费用之和。

上述参数的计算在Excel中均需使用公式表示，不能直接输入计算结果，否则Crystal Ball将无法进行分析。

至此，该网络计划项目的确定性的Excel模型建立完毕，如图2所示。在此模型的基础上，可以创建Crystal Ball项目工期和费用的风险分析模型。

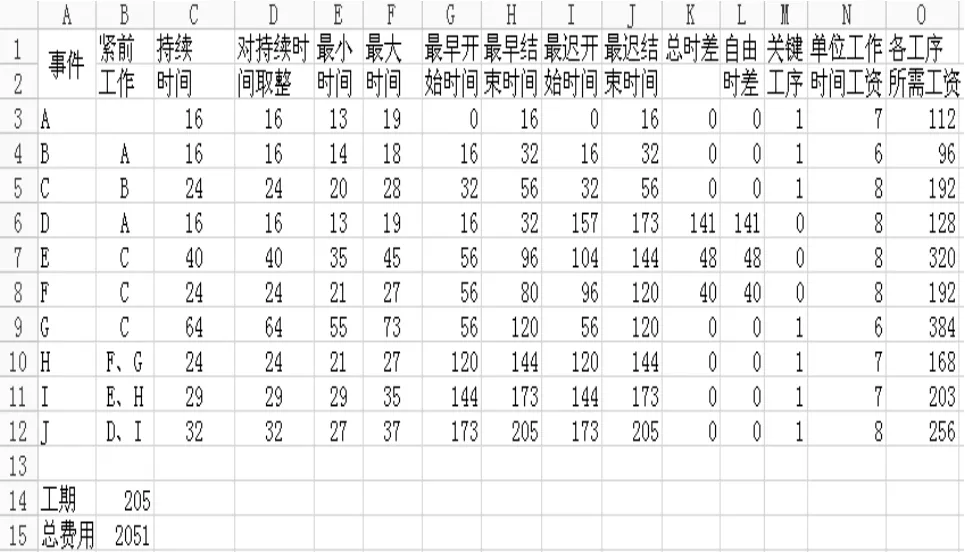
图2　网络计划的Excel模型

3　运行模拟仿真

3.1定义假设变量和预测变量

定义假设变量：对于PERT，是先假设活动持续时间服从β分布，并且采用以下近似公式计算均值和方差［16］：

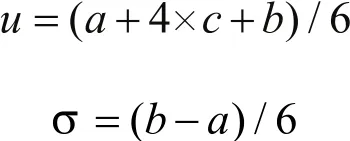
其中：a为乐观时间，完成任务所需用到的最少时间；

b为悲观时间，完成任务所需用到的最多时间；

c为最大可能时间，任务较有可能是在这段时间完成。

在Crystal Ball中，定义假设变量的是“假设单元”，用于定义不确定性的的输入量。在项目工期—费用风险分析中，因为各项任务的所需时间具有不确定性，所以需将它们定义为假设变量。

定义预测变量：即设置求解的变量。预测变量被称为 “预测单元”，是用户在指定模拟分析的过程当中用公式计算出来的值。在该项目风险分析中，工期和总费用应该设置为“预测单元”，即整个项目的工期，以及完成项目所需的总费用。选中整个项目工期单元格，点击“预测单元”， 设定参数为：Name为项目工期、Units为小时。同理定义总费用，Name为总费用，Units为元。这样预测单元就设定好了。

3.2定义运行参数

对于采用Monte-Carlo的仿真实验，实验次数可以通过大数定理来确定。在Monte-Carlo仿真实验仿真中，实际上是通过运用虚警频率逐渐逼近虚警概率，比如说在N次实验中，出现虚警次数是K次，则虚警频率为K/ N。按照大数定理，仅有当N趋向于无穷大的时候，虚警频率才会无限趋向于虚警概率。但是，按照贝努利大数定理，当实验次数N达到多少时，我们可以认定实验的虚警频率即为虚警概率。

假设虚警概率为Pf，并且希望Pf与频率K/N之间的差值小于某一给定数值ε，即：

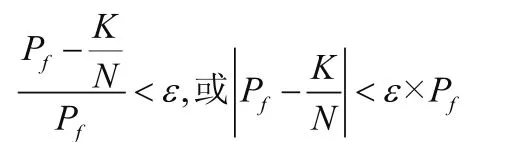
ε为足够小的常数，按照贝努利大数定理，我们可以得到：

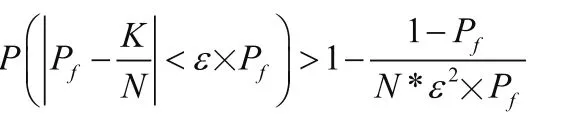
也就是说Pf与N/K之间的差值小于给定数ε的可能性将会随N的增大而不断增大，如果要使得虚警概率Pf与虚警频率K/N之间的差值小于给定常数ε的概率是P0，则么实验次数N和概率P0之间的关系为：

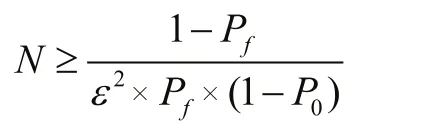
对于该项目的Monte-Carlo仿真实验，我们可以取定Pf=10-2，P0=0.9，ε=0.2 ，然后按照上面的公式计算得到N≥24750。

根据以上分析，我们可以得出如下的结论：在进行Monte-Carlo仿真实验时，如果选取的实验次数N太小，会出现实验的结果不太准确，但是如果实验次数N太大，运行时间太长，没有必要。在该项目的仿真实验中，一般取Pf=10-2就可以了，实验次数N以25000为宜。

在运行模拟仿真之前，我们根据需要，可以对模拟仿真的参数进行设置。参数有：试验次数N、什么时候运行宏、运用何种抽样方法、用哪种方式提高模拟的速度以及计算精度如何控制等。在Crystal Ball中随机数据抽样的方法有：蒙特卡洛抽样方法以及拉丁超立方抽样方法。蒙特卡洛抽样方法产生的随机数之间相互完全独立；后者则是通过几个等概率的区间来代替所设定的假设单元的概率分布。在该模拟分析中，设定置信水平为95%、试验次数设为25000次，采用蒙特卡洛抽样模拟计算。参数设定好之后，就可以进行模拟仿真了。

3.3运行模拟试验

在模拟仿真中，Crystal Ball软件通过预先设定好的试验次数N来进行大量的试验，并且在内存中保存每次试验所得到的预测值，方便随时调用，通过图表方式输出。单击“开始模拟”，开始模拟试验，Crystal Ball根据给定的原始数据模型来进行仿真计算，将建立起工期图、费用图、以及它们的敏感因素分析图和其他预先设定的图表，与此同时，EXCEL中相关的单元格中，其值将会不断变化。

4　模拟结果分析

模拟运行完成后，得到的项目工期变量的频数图，通过调整工期的上限和下限，可以得到项目工期小于27天的概率为82.88%，如图3所示。并且可以得到各个工序对工期的影响程度，可知G工序的影响程度最大，达到53.7%，如图4所示。

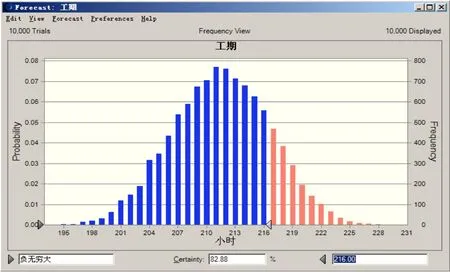
图3　工期的模拟分布结果

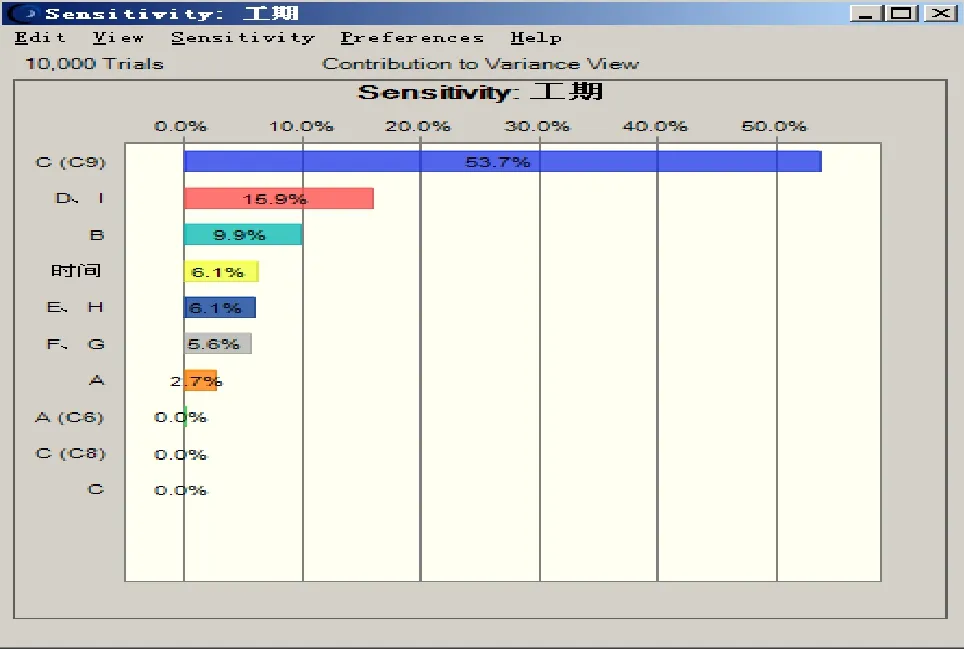
图4　工期的敏感因素分析图

同理可得总费用的统计图和各个工序对总费用的影响，总费用小于2150元的概率为84.35%，对总费用影响较大的也是G工序，影响程度达到30.5%，如图5和图6所示。

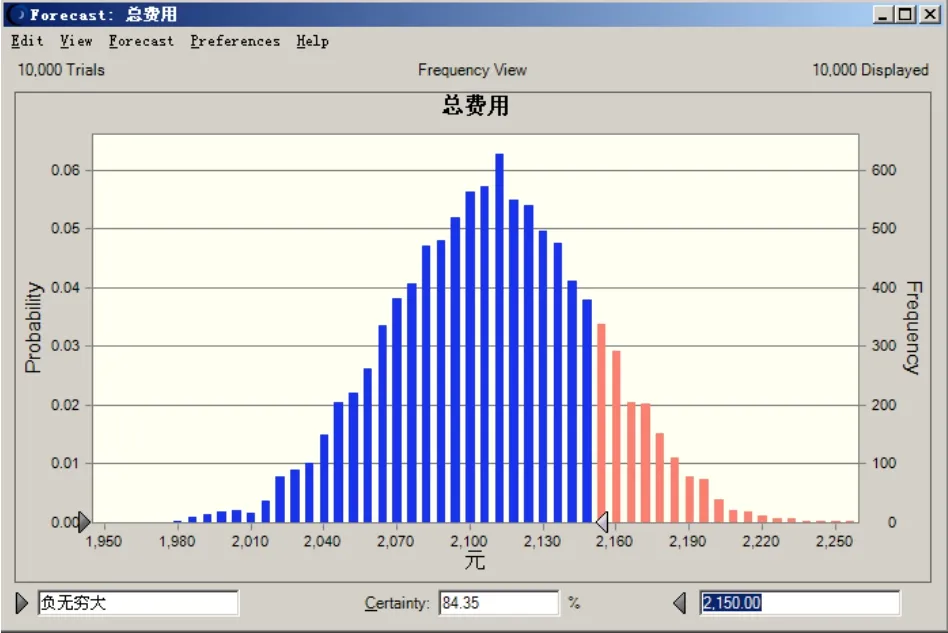
图5　总费用的模拟分布结果

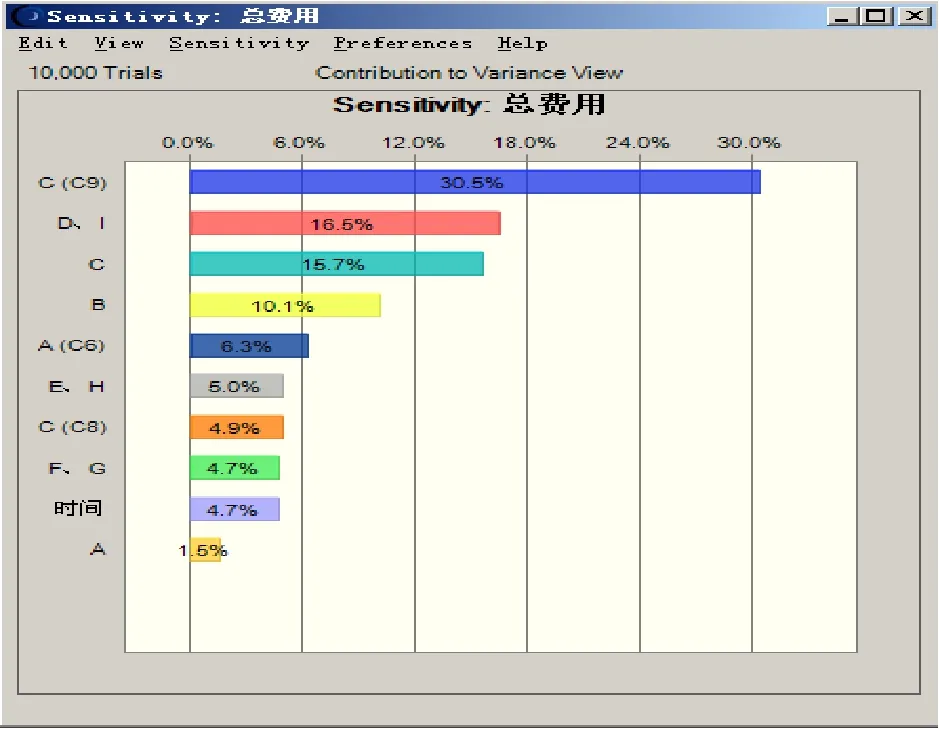
图6　总费用的敏感因素分析图

由图3可知该项目在27天内完工的概率为82.88%，尚且存在一定的延期风险。由图4可知对工期的影响中，G工序的影响为53.7%，超过一半，若要缩短该项目的工期，减少延期风险，最主要从G工序入手。

同理，由图5可知该项目的费用在预定的2150元之内的概率为84.35%，存在15.65%的可能性不能达到预定要求。由图6可知对费用的影响中，G工序的影响为30.5%，为最主要影响因素，若要减少该项目的费用，最主要从G工序入手。

5　结束语

本文综合运用运筹学、项目管理、计算机仿真以及风险分析等学科的知识，基于Crystal Ball建立网络计划项目的工期—费用风险分析模型。通过一些方法，得到该仿真模型的运行参数，从而对工期和费用进行分析，得出该项目所存在的完工风险和费用风险以及各活动持续时间的变化对项目工期和直接费用的影响程度，以便在项目进行中，对项目的各项活动进行调整优化，使项目的效益和效率都得到了提高。

本文以某个机床大修项目为例，详细介绍了基于Crystal Ball建立项目管理仿真模型，以及对项目工期—费用进行风险评估。传统的CPM/PERT方法，由于对假设存在偏差，经常导致实际结果和预测结果也存在偏差，而且没有充分考虑到一些变量的不确定性。相对于传统方法，Crystal Ball仿真更能反映项目管理中问题的本质，而且能更好地解决对不确定性变量进行定量分析的问题，成为现如今比较流行、更能贴近问题本身的风险分析技术。此外基于Crystal Ball的仿真分析方法，具有很好的可视化和灵活性，使其在现如今的风险分析中获得广泛的认可。但是该仿真技术仍然存在一定的局限性，对于很多比较复杂的系统，仿真过程比较耗时。而且仿真结果只是对真实项目的近似估计，只能得到相对较优的解决方案。

参考文献：

［1］ （美）项目管理协会.项目管理知识体系指南［M］.3版.北京：电子工业出版社，2004.

［2］ 李江，雷晓刚.基于Multi-Agent技术的大型航天研发项目风险分析方法［J］.国防科技大学学报，2012，34（6）：148-152.

［3］ 郭宇，刘尔烈.应用蒙特卡罗方法改进项目成本风险分析［J］.天津大学学报，自然科学与工程技术版，2002，35（2）：199-202.

［4］ 高建伟.基于蒙特卡罗仿真法的研究型项目风险量化分析技术［J］.科技导报，2012，30（13）：31-35.

［5］ 孟宪宽，邹磊.基于关键链的检修公司进度管理［J］.水利水电技术，2013，9（44）：80-85.

［6］ 孙金梅，刘海涛.基于Excel的网络计划技术在石化项目管理上的应用［J］.现代化工，2013，3（33）：110-112.

［7］ 杨琴，胡辉.基于Crystal Ball的项目管理建模分析［J］.中国管理信息化，综合版，2007，12（10）：27-19.

［8］ M Bevilacqua.Critical chain and risk analysis applied to high-risk industry maintenance：A Case Study［J］.International Journal of Project Management，2009，27（4）：419-432.

［9］ H Steyn.Project management applications of t he theory of constraints beyond critical chain scheduling［J］.International Journal of Project Management，2002，20（1）：75-80.

［10］ 尹齐心，余明晖，刘振元.非线性关系下的工程项目工期—成本—质量综合优化［J］.计算机应用研究，2011，28（2）：580-583.

［11］ 张静文，单绘芳.两类资源约束型工期—费用均衡及两阶段算法［J］.计算机集成制造系统，2011，17（9）：2035-2043.

［12］ 张立辉，乞建勋，仲刚.CPM网络工序工期变化对总工期影响的敏感性分析［J］.系统工程理论与实践，2010，2（30）：356-360.

［13］ 曹小琳，刘仁海.关键链项目管理缓冲区计算方法研究［J］.统计与决策，2010，3（1）：69-71.

［14］ 赵道致，王元明.基于PERT的项目工期风险传递机制［J］.工业工程，2008，11（4）：14-18.

［15］ 蒋玉石，史本山.基于Monte Carlo的口碑推荐价值改进模型研究［J］.统计与决策，2007，1（14）：147-148.

［16］ 李万庆，孟文清.工程网络计划技术［M］.北京：科学出版社，2009.

The machine overhaul project risk analysis of time limit and cost based on Monte-Carlo simulation

ZHOU Er-min， WANG Gui-yong， WANG Jian

中图分类号：TH17

文献标识码：A

文章编号：1009-0134（2016）05-0076-05

收稿日期：2015-12-04

基金项目：江西省科技计划项目：制造工艺人机环境在线仿真控制系统研究（20151BBE50053）

作者简介：周尔民（1962 -），男，江西南昌人，教授，硕士，研究方向为工业工程、虚拟制造和CAD/CAM。