两种电离层延迟改正模型对星载单频GPS实时定轨精度的影响
王甫红 郭 磊 邵晓东 龚学文
1 武汉大学测绘学院,武汉市珞喻路129号,430079
两种电离层延迟改正模型对星载单频GPS实时定轨精度的影响
王甫红1郭磊1邵晓东1龚学文1
1武汉大学测绘学院,武汉市珞喻路129号,430079
摘要:采用单频星载GPS实测伪距和载波相位观测值,结合不同的电离层延迟改正模型进行模拟实时定轨实验,分析单频实时定轨的精度。不同轨道高度的低轨卫星实验结果表明,在卫星轨道较高(500 km以上)时,使用单频伪距观测值与改进的Klobuchar模型,实时定轨位置精度可达0.86 m(三维RMS),速度精度可达0.9 mm/s,接近甚至优于双频伪距实时定轨的轨道精度;使用单频码相无电离层组合观测值时,实时定轨位置精度可达0.54 m,速度精度可达0.55 mm/s。采用合适的电离层延迟改正模型,廉价的单频星载接收机可应用于微小卫星的实时定轨。
关键词:单频;星载GPS;实时定轨;电离层延迟模型;精度分析
随着高新技术的发展以及对航天任务需求的不断扩大,成本低、性能高、快速灵活的小卫星越来越受到人们的重视[1]。由于成本、能耗、体积等限制,微小卫星上通常搭载单频GPS接收机以实现卫星轨道测控[2],如韩国遥感卫星KOMPSAT-1、英国遥感实验卫星UOSat-12、德国资源卫星BIRD等均搭载单频接收机用于确定卫星的轨道参数[2-5]。使用单频GPS接收机进行在轨实时定轨,不仅可以节约成本、降低能耗,而且能减少观测数据的存储和下传,在国内外有广泛应用。
在低轨卫星实时定轨中,电离层延迟误差是影响实时定轨精度的主要误差源之一。对于双频GPS观测数据,一般采用无电离层组合观测值,可以有效消除电离层延迟一阶项的影响。对于单频GPS观测数据,一般有两种方法:一种是采用改进的Klobuchar模型对电离层延迟进行改正[6, 7],Montenbruck等[6]将该方法应用于CHAMP卫星事后精密定轨,电离层延迟的改正效果可达90%左右;另一种是利用伪距和载波相位观测值具有电离层延迟一阶项大小相等、符号相反的特点,构建码相无电离层组合(group and phase ionosphere correction,GRAPHIC)消除电离层延迟的影响[8-10],Montenbruck等将该方法应用于GRACE卫星的事后精密定轨,定轨精度可以达到0.1 m[10]。低轨卫星星载单频GPS实时定轨,采用改进的Klobuchar模型或GRAPHIC组合对电离层延迟进行处理,其定轨策略和精度与事后精密定轨存在较大的差异。
本文选取不同轨道高度的3颗低轨卫星(350 km的CHAMP卫星、500 km的GRACE-A卫星和700 km的SAC-C卫星)的星载GPS实测数据,采用上述两种不同的电离层延迟改正方法,设计不同的定轨方案,利用自主研制的实时定轨软件模拟在轨实时定轨,分析不同电离层延迟改正方法对实时定轨精度的影响。
1两种电离层延迟改正模型
对于星载GPS测量,电离层延迟误差在天顶方向可达十几m,在高度角为5°时超过50 m。为了获得高精度的实时轨道,必须采取有效方法消除或削弱电离层延迟误差[11]。低轨卫星的轨道高度一般在160~2 000 km,不需要考虑对流层的影响。单频伪距与相位观测方程为:
(1)
式中,ρL1、ρC/A分别为L1频率上的载波相位观测值和C/A码伪距观测值,N、λ分别为L1载波整周模糊度和载波波长,δtr、δts分别为星载GPS接收机钟差和GPS卫星钟钟差,c为光速,Vion为L1频率上电离层的一阶延迟改正量,εL1、εC/A分别为载波和码的多路径误差以及观测噪声,ρgeom为接收机到GPS卫星的几何距离。
1.1改进的Klobuchar模型
低轨卫星在轨运行时,只受到轨道以上部分电离层延迟的影响,其电离层延迟改正模型和地面站的不同。2002年,Montenbruck等[6]提出了附加比例因子的Klobuchar模型,其基本思想为:假设低轨卫星轨道高度以上的残余电子集中在高度为hIP(hIP>hs)的薄层上,GPS卫星和低轨卫星的连线与薄层的交点为P。GPS卫星相对于穿刺点P的高度角为EIP,则GPS信号传播方向上的电离层延迟改正量可以表示为:
(2)
式中,f1为L1载波的频率;M(EIP)为投影函数,作用是实现垂直方向的总电子含量和信号传播路径上的总电子含量之间的转换;VTEC(λIP,φIP,0)为穿刺点处地面以上垂直方向的总电子含量,可以利用Klobuchar模型计算得到;α为低轨卫星轨道高度以上的电子总含量TEC(λIP,φIP,hIP)和地面以上的总电子含量TEC(λIP,φIP,0)的比值,可用Chapman电子剖面密度函数计算得到:
(3)
式中,e为常数2.718 28,exp表示e的指数函数;zIP=(hs-h0)/H,hs为低轨卫星距地面的高度,h0为电子密度峰值高度;H为电子密度高度变化率,取100 km。这种电离层延迟改正量的计算方法称为改进的Klobuchar模型。
1.2GRAPHIC组合
根据同一频率上码伪距和载波相位观测值的电离层延迟一阶项大小相等、符号相反的特点,对载波相位和码伪距观测值求均值,可以有效消除电离层延迟一阶项的影响。组合观测方程可以表示为:
(4)
式中,ρC1L1即为GRAPHIC组合观测值,ε为组合观测值噪声。
GRAPHIC组合不但能够消除电离层延迟一阶项的影响,而且能够降低观测噪声。其观测噪声的标准差可以表示为:
(5)
如果忽略载波相位观测值的噪声,GRAPHIC组合的观测噪声仅为C/A码伪距观测值噪声的一半。
该方法解算过程中引入了载波相位观测值,因此必须考虑周跳的影响。本文周跳探测使用一种基于粗差探测理论的GPS相位周跳探测方法,即VAREC方法[12]。
2实时定轨参数估计
实时定轨[13]的算法是以星载GPS跟踪数据作为测量值,结合动力学模型,用推广卡尔曼滤波估计卫星的状态。采用改进的Klobuchar模型进行实时定轨时,其待估参数为:
(6)
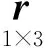
若使用GRAPHIC组合消除电离层延迟的影响,实时定轨过程中由于引入了载波相位观测值,除了前面所述的参数,还需要对每一颗观测卫星增加一个模糊度参数。那么,待估向量拓展为:
(7)
在精密单点定位或精密定轨中,模糊度通常作为一个常数求解[14],但是在实时定轨中一般使用广播星历。广播星历中的卫星钟误差和卫星位置误差在观测视线上的投影与模糊度参数无法准确分离,因此,在实时定轨滤波估计中,模糊度参数实际上包括了卫星钟误差和位置误差。本文将每颗卫星的模糊度参数用随机游走过程模拟。模糊度参数的初值为N=ρC/A-ρL1-2Vion,其中电离层延迟Vion由改进的Klobuchar模型计算给出,其动态过程噪声协方差矩阵为:
(8)
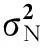
3实验及结果分析
3.1实验数据与定轨方案
本文实验数据选用轨道高度分别为350km、500km与700km的CHAMP、GRACE-A与SAC-C卫星连续7d(2006年年积日251~257)的星载GPS实测数据,利用自主研制的实时定轨软件SATODS进行连续实时定轨数据处理。所有实时定轨结果与JPL提供的事后精密轨道进行比较,分析实时定轨精度。
设计两种不同的单频定轨方案,如表1所示。方案1利用C/A码伪距观测值,采用改进的Klobuchar模型改正电离层延迟进行实时定轨;方案2利用GRAPHIC组合观测值来消除电离层延迟一阶项的影响。同时,给出传统的双频伪距观测值实时定轨结果,作为方案1和2的参照,对比单频实时定轨与双频伪距定轨的精度差异。为了便于比较,3次数据处理过程中所采用的动力学模型设置和具体定轨策略都完全相同,如表2所示。

表1 两种单频定轨方案观测模型

表2 定轨策略设置
3.2实时定轨精度及分析
表3给出了2006年年积日=251~257期间不同轨道高度的卫星使用上述方案实时定轨的三维位置误差RMS统计。可以看出,对于轨道高度为350 km的CHAMP卫星,使用改进的Klobuchar模型可以获得1.10 m的定轨位置精度,比双频伪距观测值实时定轨精度0.93 m略差;对于轨道高度为500 km的GRACE-A卫星,使用改进的Klobuchar模型可以获得0.77 m的定轨位置精度,与双频伪距实时定轨位置精度0.73 m相当;对于轨道高度为700 km的SAC-C卫星,使用改进的Klobuchar模型可以获得0.86 m的位置精度,优于双频伪距实时定轨0.96 m的位置精度。随着卫星轨道高度的增加(大于500 km时),使用改进的Klobuchar模型实时定轨可以获得与双频伪距观测值实时定轨精度相当甚至更优的结果。
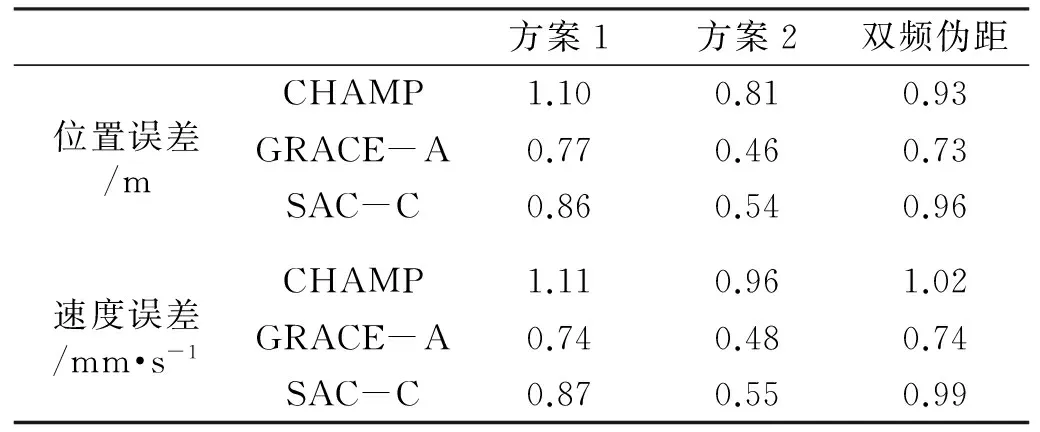
表3 不同高度卫星使用不同方案得到的实时定轨精度
方案2使用GRAPHIC组合消除电离层延迟一阶项的影响,无论卫星轨道高低,其实时定轨结果均优于方案1和双频伪距实时定轨的结果。CHAMP卫星使用GRAPHIC组合观测值,实时定轨位置精度可达0.81 m,速度精度可达0.96 mm/s,相对于双频伪距实时定位精度(0.93 m,1.03 mm/s)提高了约13%;GRACE-A和SAC-C卫星有类似的结果,定轨精度分别提高了37%和42%。
具体分析每天实时定轨结果的误差情况,图1给出了CHAMP、GRACE-A和SAC-C卫星2006年年积日253使用方案1、双频伪距实时定轨结果在径向(R)、切向(T)与法向(N)上的位置误差曲线。可以看出,方案1采用改进的Klobuchar模型,3颗卫星实时定轨结果的法向误差与双频伪距实时定轨结果法向误差曲线吻合较好;但对于径向与切向误差,卫星轨道越高,方案1与双频伪距实时定轨误差曲线吻合得越好,尤其在径向,轨道高度在700 km以上的SAC-C卫星曲线吻合最好。这说明,轨道高度越高,电离层延迟影响就越小,单频伪距实时定轨可达到甚至优于双频伪距实时定轨的精度水平。
图2给出了方案2和双频伪距实时定轨下CHAMP、GRACE-A和SAC-C卫星在2006年年积日253时实时定轨结果的位置误差曲线。方案2和双频伪距实时定轨采用不同的组合观测值,均有效消除了电离层延迟一阶项的影响。对于CHAMP卫星,双频伪距实时定轨结果的径向、切向与法向误差分别优于±0.93 m、±2.50 m、±1.20 m,而方案2实时定轨结果的径向、切向、法向误差分别优于±0.85 m、±2.10 m、±1.05 m;对于GRACE-A和SAC-C卫星,定轨结果有类似的情况。无论卫星轨道的高低,相比于双频伪距实时定轨,方案2采用GRAPHIC组合观测值,其实时定轨结果在径向与切向误差大幅度减小,可以获得较高精度的定轨结果。分析其原因,使用GRAPHIC组合不仅消除了电离层延迟一阶项的影响,而且组合观测值噪声仅为C/A码伪距观测值的一半。同时,由于滤波中增加了模糊度参数,通过设计模糊度参数的随机模型,可以吸收广播星历中缓慢变化的卫星轨道误差和钟差误差,从而提高实时定轨的精度。

图1 不同高度卫星使用方案1和双频伪距实时定轨位置误差曲线(2006年年积日253)Fig.1 Real-time orbit determination results of method 1 and double-frequency GPS observations (DOY 253,2006)

图2 不同高度卫星使用方案2和双频伪距实时定轨位置误差(2006年年积日253)Fig.2 Real-time orbit determination results of method 2 and double-frequency GPS observations (DOY 253,2006)
4结语
本文采用不同轨道高度的3颗低轨卫星(CHAMP、GRACE-A与SAC-C)的星载GPS实测数据进行实时定轨实验,利用两种不同的电离层延迟改正模型削弱或消除电离层延迟的影响,分析不同电离层延迟改正方法对低轨卫星单频星载GPS实时定轨精度的影响。得出:
1)当卫星轨道较高(500 km以上)时,使用改进的Klobuchar模型改正电离层延迟,单频星载GPS实时定轨的位置精度可达0.8~0.9 m,定轨精度与双频伪距实时定轨结果相当,甚至略有提高。
2)无论卫星轨道高低,使用GRAPHIC组合消除电离层延迟一阶项影响,实时定轨可以获得较高的定轨精度。
使用改进的Klobuchar模型改正电离层延迟,算法简单,易于实现,但定轨精度较低。使用GRAPHIC组合,实时定轨可以获得较高的精度,但该方法引入了载波相位数据,增加了模糊度参数,待估状态向量维数扩大,计算复杂度增加。因此,下一步有必要验证该方法在星载平台上实时自主运行的可行性。
参考文献
[1]詹亚锋,马正新,曹志刚.现代微小卫星技术及发展趋势[J].电子学报, 2000(7): 102-107(Zhan Yafeng,Ma Zhengxin, Cao Zhigang. Technology of Modern Micro Satellite and Its Development Direction[J]. Aata Electronica Sinica, 2000(7): 102-107)
[2]Sandau R, Roser H, Valenzuela A. Small Satellites for Earth Observations[M].Springer Netherlands,2008
[3]郭向,张强,赵齐乐,等.基于单频星载GPS数据的低轨卫星精密定轨[J].中国空间科学技术, 2013(2): 41-46(Guo Xiang, Zhang Qiang, Zhao Qile, et al.Precise Orbit Determination for LEO Satellites Using Single-Frequency GPS Observations[J].Chinese Space Science and Technology,2013(2):41-46)[4]Yoon J, Roh K, Park E, et al. Orbit Determination of Spacecraft Using Global Positioning System Single-Frequency Measurement[J]. Journal of Spacecraft and Rockets, 2002, 39(5): 796 - 801
[5]Gill E, Montenbruck O, Brie β. GPS-Based Autonomous Navigation for the BIRD Satellite[C]. 15th International Symposium on Spaceflight Dynamics, Biarritz, 2000
[6]Montenbruck O, Gill E. Ionospheric Correction for GPS Tracking of LEO Satellites[J]. The Journal of Navigation, 2002, 55(2): 293-304
[7]彭冬菊,吴斌. GIM在LEO卫星单频GPS定轨中的应用[J]. 天文学报, 2012(1): 36-50(Peng Dongju, Wu Bin. The Application of GIM in Precise Orbit Determination for LEO Satellites with Single-Frequency GPS Measurements[J]. Acta Astronomica Sinica, 2012(1): 36-50)
[8]Bock H, Jäggi A, Dach R, et al. GPS Single-Frequency Orbit Determination for Low Earth Orbiting Satellites[J]. Advances in Space Research, 2009, 43(5): 783-791
[9]Montenbruck O, Ramos-Bosch P. Precision Real-Time Navigation of LEO Satellites Using Global Positioning System Measurements[J]. GPS Solutions, 2008, 12(3): 187-198[10]Montenbruck O,Helleputte T, Kroes R, et al. Reduced Dynamic Orbit Determination Using GPS Code and Carrier Measurements[J]. Aerospace Science and Technology, 2005, 9(3): 261-271
[11]李征航,黄劲松. GPS测量与数据处理[M].武汉: 武汉大学出版社, 2005(Li Zhenghang,Huang Jinsong. GPS Surveying and Data Processing[M].Wuhan:Wuhan Universiay Press,2005)
[12]王甫红,刘基余. 星载GPS载波相位测量的周跳探测方法研究[J]. 武汉大学学报:信息科学版, 2004,29(9): 772-774(Wang Fuhong, Liu Jiyu. A New Algorithm Detecting Cycle Slips in Satellites Borne GPS Carrier Phase Measurements for Precise Orbit Determination[J]. Geomatics and Information Science of Wuhan University, 2004,29(9): 772-774)
[13]王甫红. 星载GPS自主定轨理论及其软件实现[D].武汉:武汉大学,2006(Wang Fuhong. Theory and Software Development on Autonomous Orbit Determination with Space-Borne GPS Measurements[D].Wuhan: Wuhan University, 2006)[14]Simsky A. Standalone Real-Time Navigation Algorithm for Single-Frequency Ionosphere-Free Positioning Based on Dynamic Ambiguities (DARTS-SF)[C]. 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, 2006
Foundation support:National Natural Science Foundation of China,No. 41374035.
About the first author:WANG Fuhong,PhD, associate professor,majors in satellite navigation and orbit determination, E-mail:fhwang@sgg.whu.edu.cn.
Effects Analysis of Two Ionosphere Correction Models on Space-Borne GPS Single-Frequency Real-Time Orbit Determination
WANGFuhong1GUOLei1SHAOXiaodong1GONGXuewen1
1School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road,Wuhan 430079, China
Abstract:The ionosphere range delay is one of the dominating error sources for the space-borne GPS single-frequency real-time orbit determination. When corrected by ionosphere correction models, the residual error has obvious influence on the accuracy of real-time orbit determination. In this paper, we use single-frequency pseudo-range and carrier phase measurements, calculated with two different ionosphere correction models, and then we analyze their impacts on the results. Our study shows that when the altitude of the low earth orbit (LEO) satellites is 500 km or higher, the position and velocity accuracy (3DRMS) are 0.86 m and 0.9 mm/s, which is close to the accuracy of dual-frequency pseudo-range real-time orbit determination. When using the group and phase ionosphere correction (GRAPHIC), the position and velocity accuracy can be 0.54 m and 0.55 mm/s. Therefore, when an appropriate ionosphere correction model is selected, low-cost single-frequency space-borne GPS receivers can be used in real-time orbit determination for micro-satellites.
Key words:single-frequency;space-borne GPS;real-time orbit determination;ionosphere correction models;accuracy analysis
收稿日期:2015-07-01
第一作者简介:王甫红,博士,副教授,主要从事卫星导航定位和卫星定轨方法研究,E-mail:fhwang@sgg.whu.edu.cn。
DOI:10.14075/j.jgg.2016.07.001
文章编号:1671-5942(2016)07-0565-05
中图分类号:P228
文献标识码:A
项目来源:国家自然科学基金(41374035)。

